Алгоритм масштабирования потока — различия между версиями
(→Оценка сложности) |
м (rollbackEdits.php mass rollback) |
||
| (не показаны 72 промежуточные версии 8 участников) | |||
| Строка 1: | Строка 1: | ||
| − | + | == Алгоритм == | |
| − | + | Пусть дана [[Определение_сети,_потока#.D0.9E.D0.BF.D1.80.D0.B5.D0.B4.D0.B5.D0.BB.D0.B5.D0.BD.D0.B8.D0.B5_.D1.81.D0.B5.D1.82.D0.B8|сеть]] <tex> G </tex>, все рёбра которой имеют целочисленную [[Определение_сети,_потока#.D0.9E.D0.BF.D1.80.D0.B5.D0.B4.D0.B5.D0.BB.D0.B5.D0.BD.D0.B8.D0.B5_.D1.81.D0.B5.D1.82.D0.B8|пропускную способность]]. Обозначим за <tex> U </tex> максимальную пропускную способность: <tex> U = \max\limits_{(u, v) \in E} c(u, v) </tex>. | |
| − | |||
| − | |||
| − | |||
| − | + | Идея алгоритма заключается в нахождении путей с высокой пропускной способностью в первую очередь, чтобы сразу сильно увеличивать [[Определение_сети,_потока#.D0.9E.D0.BF.D1.80.D0.B5.D0.B4.D0.B5.D0.BB.D0.B5.D0.BD.D0.B8.D0.B5_.D0.BF.D0.BE.D1.82.D0.BE.D0.BA.D0.B0|поток]] по ним, а затем по всем остальным. Для этого воспользуемся масштабом <tex> \Delta </tex>. Изначально положим <tex> \Delta = 2^{\lfloor \log_2 U \rfloor} </tex>. | |
| − | Идея алгоритма в нахождении путей с высокой пропускной способностью в первую очередь, чтобы сразу сильно увеличивать поток по ним, а затем по всем остальным. | ||
| − | + | На каждой итерации в [[Дополняющая_сеть,_дополняющий_путь|дополняющей сети]] алгоритм находит [[Дополняющая_сеть,_дополняющий_путь|дополняющие пути]] с пропускной способностью не меньшей <tex> \Delta </tex> и увеличивает поток вдоль них. | |
| − | <tex> | + | Уменьшив масштаб <tex> \Delta </tex> в <tex> 2 </tex> раза, переходит к следующей итерации. |
| − | <tex> | + | Очевидно, что при <tex> \Delta = 1 </tex> алгоритм вырождается в алгоритм [[Алоритм_Эдмондса-Карпа|Эдмондса-Карпа]], вследствие чего является корректным. |
| − | + | Количество необходимых увеличений путей, основанных на кратчайших путях, может быть много больше количества увеличений, основанных на путях с высокой пропускной способностью. | |
| − | + | {|border="0" cellpadding="5" width=30% align=center | |
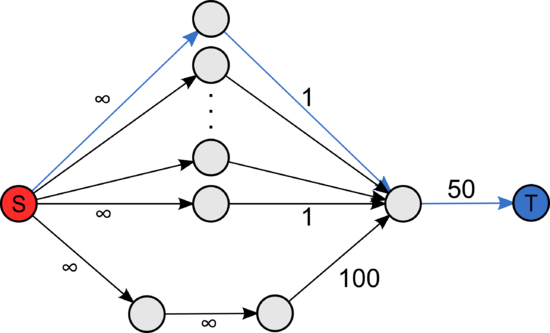
| + | |[[Файл:Flow_scale_1.png|550px|thumb|center|Выбор дополняющих путей в порядке длины]] | ||
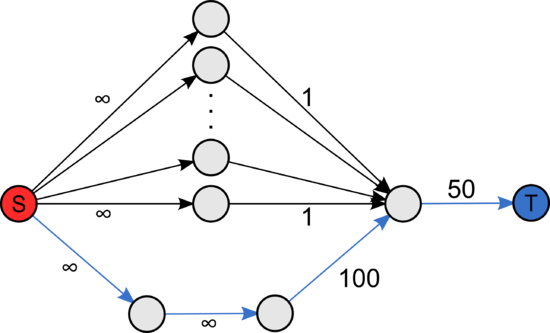
| + | |[[Файл:Flow_scale_2.png|550px|thumb|center|Выбор пути с высокой пропускной способностью в первую очередь]] | ||
| + | |} | ||
| − | + | == Оценка времени работы == | |
| − | + | {{Лемма | |
| − | == Оценка | + | |about= |
| − | {{ | + | 1 |
|statement= | |statement= | ||
| − | + | Максимальный поток в сети <tex> G </tex> ограничен сверху значением <tex> |f_k| + 2^k E </tex>, где <tex> |f_k| </tex> {{---}} значение потока при масштабе <tex> \Delta = 2^k </tex>. | |
|proof= | |proof= | ||
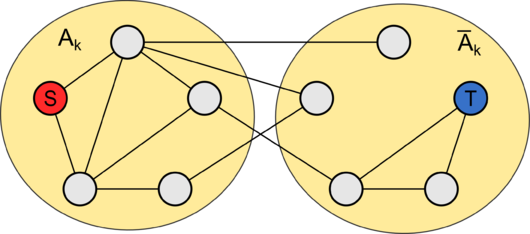
| − | + | [[Файл:Flow_scale_3.png|530px|thumb|right|Разрез <tex> C_k </tex>]] | |
| + | |||
| + | В конце итерации с масштабом <tex> \Delta = 2^k </tex>, сеть <tex> G_{f_k} </tex> может быть разбита на два непересекающихся множества <tex> A_k </tex> и <tex> \overline{A_k} </tex> так, что остаточная пропускная способность каждого ребра, идущего из <tex> A_k </tex> в <tex> \overline{A_k} </tex>, не превосходит масштаба <tex> \Delta </tex>. То есть образуется [[Разрез,_лемма_о_потоке_через_разрез|разрез]] <tex> C_k = \langle A_k, \overline{A_k} \rangle </tex>. | ||
| + | |||
| + | При этом, количество таких рёбер не превосходит <tex> E </tex>. | ||
| + | Значит, значение остаточного потока не может превосходить <tex> \Delta E = 2^k E </tex>. | ||
| + | }} | ||
{{Лемма | {{Лемма | ||
| + | |about= | ||
| + | 2 | ||
|statement= | |statement= | ||
| − | + | Суммарное количество увеличивающих путей {{---}} <tex> O(E \log U) </tex>. | |
|proof= | |proof= | ||
| − | На | + | На некоторой итерации алгоритма каждый дополняющий путь имеет пропускную способность не меньше <tex> 2^k </tex>. |
| − | }} | + | Дополняющий поток на предыдущем шаге ограничен значением <tex> 2^{k + 1} E </tex>. Следовательно, на каждой итерации количество дополняющих путей не превосходит <tex> 2E </tex>.}} |
| − | + | {{Утверждение | |
| − | {{ | ||
|statement= | |statement= | ||
| − | + | Время работы алгоритма {{---}} <tex> O(E^2 \log U) </tex>. | |
|proof= | |proof= | ||
| − | + | В ходе выполнения алгоритма масштаб <tex> \Delta </tex> принимает следующие значения: <tex> S = \{2^{\lfloor \log_2 U \rfloor}, \ldots, 2^k, \ldots, 2, 1, 0\} </tex>. Тогда <tex> |S| = O(\log U) </tex> {{---}} количество итераций алгоритма. | |
| − | |||
| − | |||
| − | + | Количество итераций алгоритма {{---}} <tex> O(\log U) </tex>, значит, суммарное количество увеличивающих путей {{---}} <tex> O(E \log U) </tex>. | |
| − | <tex> \ | ||
| − | + | Алгоритм [[Обход_в_ширину|обхода в ширину]] находит каждый дополняющий путь за время <tex> O(E) </tex>. Следовательно, суммарное время работы алгоритма {{---}} <tex> O(E^2 \log U) </tex>.}} | |
| − | <tex> \ | + | |
| − | <tex> | + | == Псевдокод == |
| − | + | '''function''' maxFlowByScaling(G: '''graph''', s: '''int''', t: '''int'''): '''int''' | |
| − | + | '''int''' flow = 0 <font color=darkgreen> // поток в сети </font> | |
| + | '''int''' scale = <tex>2^{\lfloor\log_2U\rfloor}</tex> <font color=darkgreen> // текущий минимальный размер потока, который пытаемся пустить </font> | ||
| + | '''while''' scale <tex> \geqslant </tex> 1 | ||
| + | '''while''' в <tex> G_f </tex> существует увеличивающий путь <tex> p </tex> с пропускной способностью не меньше, чем scale | ||
| + | '''int''' minCapacity = <tex>\min\{c(u, v) \colon(u, v) \in p\} </tex> <font color=darkgreen> // минимальная пропускная способность в увеличивающем пути </font> | ||
| + | увеличить поток по рёбрам <tex> p </tex> на minCapacity | ||
| + | обновить <tex> G_f </tex> | ||
| + | flow = flow + minCapacity | ||
| + | scale = scale / 2 | ||
| + | '''return''' flow | ||
| − | + | == См. также == | |
| − | + | * [[Определение_сети,_потока|Определение сети, потока]] | |
| + | * [[Алоритм_Эдмондса-Карпа|Алоритм Эдмондса-Карпа]] | ||
| + | * [[Алгоритм_Форда-Фалкерсона,_реализация_с_помощью_поиска_в_глубину|Алгоритм Форда-Фалкерсона]] | ||
| − | == | + | == Источники информации == |
* [http://www.csd.uwo.ca/~yuri/Papers/iccv07_cap_scaling.pdf ''Olivier Juan, Yuri Boikov'': Capacity Scaling for Graph Cuts in Vision] | * [http://www.csd.uwo.ca/~yuri/Papers/iccv07_cap_scaling.pdf ''Olivier Juan, Yuri Boikov'': Capacity Scaling for Graph Cuts in Vision] | ||
* [http://www.topcoder.com/tc?module=Static&d1=tutorials&d2=maxFlowRevisited Algorithm Tutorials. Maximum Flow: Augmenting Path Algorithms Comparison] | * [http://www.topcoder.com/tc?module=Static&d1=tutorials&d2=maxFlowRevisited Algorithm Tutorials. Maximum Flow: Augmenting Path Algorithms Comparison] | ||
| − | * [http:// | + | * [http://logic.pdmi.ras.ru/ics/talks/21stream.pdf ''Андрей Станкевич'': Задача о максимальном потоке] |
| + | * [https://youtu.be/sEwp5ZAJJps?t=18m9s ''Андрей Станкевич'': Лекториум, дополнительные главы алгоритмов, лекция 12] | ||
| + | |||
| + | [[Категория: Алгоритмы и структуры данных]] | ||
| + | [[Категория: Задача о максимальном потоке]] | ||
Текущая версия на 19:21, 4 сентября 2022
Алгоритм
Пусть дана сеть , все рёбра которой имеют целочисленную пропускную способность. Обозначим за максимальную пропускную способность: .
Идея алгоритма заключается в нахождении путей с высокой пропускной способностью в первую очередь, чтобы сразу сильно увеличивать поток по ним, а затем по всем остальным. Для этого воспользуемся масштабом . Изначально положим .
На каждой итерации в дополняющей сети алгоритм находит дополняющие пути с пропускной способностью не меньшей и увеличивает поток вдоль них. Уменьшив масштаб в раза, переходит к следующей итерации.
Очевидно, что при алгоритм вырождается в алгоритм Эдмондса-Карпа, вследствие чего является корректным.
Количество необходимых увеличений путей, основанных на кратчайших путях, может быть много больше количества увеличений, основанных на путях с высокой пропускной способностью.
Оценка времени работы
| Лемма (1): |
Максимальный поток в сети ограничен сверху значением , где — значение потока при масштабе . |
| Доказательство: |
|
В конце итерации с масштабом , сеть может быть разбита на два непересекающихся множества и так, что остаточная пропускная способность каждого ребра, идущего из в , не превосходит масштаба . То есть образуется разрез . При этом, количество таких рёбер не превосходит . Значит, значение остаточного потока не может превосходить . |
| Лемма (2): |
Суммарное количество увеличивающих путей — . |
| Доказательство: |
|
На некоторой итерации алгоритма каждый дополняющий путь имеет пропускную способность не меньше . Дополняющий поток на предыдущем шаге ограничен значением . Следовательно, на каждой итерации количество дополняющих путей не превосходит . |
| Утверждение: |
Время работы алгоритма — . |
|
В ходе выполнения алгоритма масштаб принимает следующие значения: . Тогда — количество итераций алгоритма. Количество итераций алгоритма — , значит, суммарное количество увеличивающих путей — . Алгоритм обхода в ширину находит каждый дополняющий путь за время . Следовательно, суммарное время работы алгоритма — . |
Псевдокод
function maxFlowByScaling(G: graph, s: int, t: int): int
int flow = 0 // поток в сети
int scale = // текущий минимальный размер потока, который пытаемся пустить
while scale 1
while в существует увеличивающий путь с пропускной способностью не меньше, чем scale
int minCapacity = // минимальная пропускная способность в увеличивающем пути
увеличить поток по рёбрам на minCapacity
обновить
flow = flow + minCapacity
scale = scale / 2
return flow