Фибоначчиева куча — различия между версиями
Rybak (обсуждение | вклад) |
м (rollbackEdits.php mass rollback) |
||
| (не показано 58 промежуточных версий 21 участника) | |||
| Строка 1: | Строка 1: | ||
| − | = | + | '''Фибоначчиева куча''' (англ. ''Fibonacci heap'') {{---}} структура данных, отвечающая интерфейсу [[Приоритетные очереди#Операции | приоритетная очередь]]. Эта структура данных имеет меньшую [[Амортизационный анализ#Основные определения | амортизированную сложность]], чем такие приоритетные очереди как [[Биномиальная куча | биномиальная куча]] и [[Двоичная куча | двоичная куча]]. Изначально эта структура данных была разработана Майклом Фридманом<ref>[[wikipedia:en:Michael_Fredman | Майкл Фридман {{---}} Википедия]]</ref> и Робертом Тарьяном<ref>[[wikipedia:en:Robert_Tarjan | Роберт Тарьян {{---}} Википедия]]</ref> при работе по улучшению асимптотической сложности [[Алгоритм Дейкстры | алгоритма Дейкстры]]. Свое название Фибоначчиева куча получила из-за использования некоторых свойств чисел Фибоначчи<ref>[[wikipedia:en:Fibonacci_number | Числа Фибоначчи {{---}} Википедия]]</ref> в [[Амортизационный анализ#Метод потенциалов | потенциальном анализе]] этой реализации. |
| + | == Структура == | ||
| + | Фибоначчиева куча {{---}} набор из [[Дерево, эквивалентные определения | подвешенных деревьев]] удовлетворяющих свойству: каждый предок не больше своих детей(если дерево на минимум). Это означает, что минимум всей кучи это один из корней этих деревьев. Одно из главных преимуществ Фибоначчиевой кучи {{---}} гибкость её структуры из-за того, что на деревья не наложены никакие ограничения по форме. Например, Фибоначчиева куча может состоять хоть из деревьев в каждом из которых по одному элементу. Такая гибкость позволяет выполнять некоторые операции лениво, оставляя работу более поздним операциям. Далее будут даны некоторые определения, которые понадобятся в дальнейшем. | ||
{{Определение | {{Определение | ||
|definition= | |definition= | ||
| − | ''' | + | '''Степень вершины''' (англ. ''degree'') {{---}} количество детей данной вершины. Далее будем обозначать как <tex>degree(x)</tex>, где <tex>x</tex> это вершина. |
}} | }} | ||
{{Определение | {{Определение | ||
|definition= | |definition= | ||
| − | ''' | + | '''Степень кучи''' (англ. ''degree'') {{---}} наибольшая степень вершины этой кучи. Далее будем обозначать как <tex>degree(H)</tex>, где <tex>H</tex> это куча. |
}} | }} | ||
| + | == Реализация == | ||
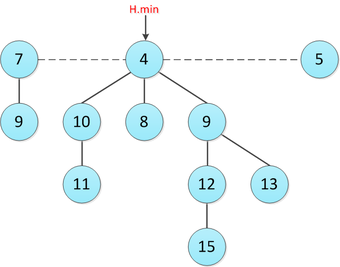
| + | [[File:Fibonacci-heap.png|thumb|340px|Пример фибоначчиевой кучи]] | ||
| + | Для возможности быстрого удаления элемента из произвольного места и объединением с другим списком будем хранить их в [[Список#Циклический список | циклическом двусвязном списке]]. Также будем хранить и все уровни поддерева. Исходя из этого структура каждого узла будет выглядеть вот так. | ||
| + | <code style="display:inline-block"> | ||
| + | '''struct''' Node | ||
| + | '''int''' key <span style="color:#008000"> // ключ</span> | ||
| + | '''Node''' parent <span style="color:#008000"> // указатель на родительский узел</span> | ||
| + | '''Node''' child <span style="color:#008000"> // указатель на один из дочерних узлов</span> | ||
| + | '''Node''' left <span style="color:#008000"> // указатель на левый узел того же предка</span> | ||
| + | '''Node''' right <span style="color:#009000"> // указатель на правый узел того же предка</span> | ||
| + | '''int''' degree <span style="color:#008000"> // степень вершины</span> | ||
| + | '''boolean''' mark <span style="color:#008000">// был ли удален в процессе изменения ключа ребенок этой вершины)</span> | ||
| + | </code>Также стоит упомянуть, что нам нужен указатель только на одного ребенка, поскольку остальные хранятся в двусвязном списке с ним. Для доступа ко всей куче нам тоже нужен всего один элемент, поэтому разумно хранить именно указатель на минимум кучи (он обязательно один из корней), а для получения размера за константное время будем хранить размер кучи отдельно. | ||
| + | <code style="display:inline-block"> | ||
| + | '''struct''' fibonacciHeap | ||
| + | '''int''' size <span style="color:#008000">// текущее количество узлов</span> | ||
| + | '''Node''' min <span style="color:#008000">// указатель на корень дерева с минимальным ключом</span> | ||
| + | </code> | ||
| + | ==== Cоздание кучи ==== | ||
| + | Инициализация кучи. | ||
| + | <code style="display:inline-block"> | ||
| + | '''function''' buildHeap: | ||
| + | min <tex>= \varnothing</tex> | ||
| + | size = 0 | ||
| + | </code> | ||
| + | ==== Вставка элемента ==== | ||
| + | Данная операция вставляет новый элемент в список корней правее минимума и при необходимости меняет указатель на минимум кучи. | ||
| + | <code style="display:inline-block"> | ||
| + | '''function''' insert(x: '''int'''): | ||
| + | '''Node''' newNode <span style="color:#008000"> // создаем новый узел</span> | ||
| + | newNode.key = x <span style="color:#008000"> // инициализируем ключ нового узла</span> | ||
| + | '''if''' size = 0 <span style="color:#008000"> // если куче нет элементов, то только что добавленный минимальный</span> | ||
| + | min = newNode | ||
| + | min.left = newNode | ||
| + | min.right = newNode | ||
| + | '''else'''<span style="color:#008000"> // иначе аккуратно меняем указатели в списке, чтобы не перепутать указатели</span> | ||
| + | '''Node''' prevRight = min.right | ||
| + | min.right = newNode | ||
| + | newNode.left = min | ||
| + | newNode.right = prevRight | ||
| + | prevRight.left = newNode | ||
| + | '''if''' newNode.key < min.key | ||
| + | min = newNode <span style="color:#008000"> // меняем указатель на минимум, если надо</span> | ||
| + | newNode.parent <tex>= \varnothing</tex> | ||
| + | size++ <span style="color:#008000"> // не забываем увеличить переменную size </span> | ||
| + | </code> | ||
| + | ==== Получение минимального элемента ==== | ||
| + | Получение минимума всей кучи. | ||
| + | <code style="display:inline-block"> | ||
| + | '''int''' getMin: | ||
| + | '''return''' min.key | ||
| + | </code> | ||
| + | ==== Соедининение двух куч ==== | ||
| + | Для сливания двух Фибоначчиевых куч необходимо просто объединить их корневые списки, а также обновить минимум новой кучи, если понадобится. Вынесем в вспомогательную функцию <tex>unionLists</tex> логику, объединяющую два списка вершины, которых подаются ей в качестве аргументов. | ||
| + | <code style="display:inline-block"> | ||
| + | '''function''' unionLists(first: '''Node''', second: '''Node'''): | ||
| + | '''Node''' L = first.left <span style="color:#008000"> // аккуратно меняем указатели местами указатели</span> | ||
| + | '''Node''' R = second.right | ||
| + | second.right = first | ||
| + | first.left = second | ||
| + | L.right = R | ||
| + | R.left = L | ||
| + | </code> | ||
| + | Сливаем два корневых списка в один и обновляем минимум, если нужно. | ||
| + | <code style="display:inline-block"> | ||
| + | '''function''' merge(that: '''fibonacciHeap'''): | ||
| + | '''if''' that.size = 0 <span style="color:#008000"> // если вторая куча пуста, нечего добавлять</span> | ||
| + | '''return''' | ||
| + | '''if''' size = 0 <span style="color:#008000"> // если наша куча пуста, то результатом будет вторая куча</span> | ||
| + | min = that.min | ||
| + | size = that.size | ||
| + | '''else''' | ||
| + | unionLists(min, that.min) <span style="color:#008000"> // объединяем два корневых списка</span> | ||
| + | size += that.size | ||
| + | '''if''' min <tex>= \varnothing</tex> '''or''' (that.min <tex> \neq \varnothing</tex> '''and''' that.min < min) <span style="color:#008000">// если минимум кучи изменился, то надо обновить указатель</span> | ||
| + | min = that.min | ||
| + | </code> | ||
| + | |||
| + | ==== Удаление минимального элемента==== | ||
| + | Первая рассматриваемая операция, в ходе которой значительно меняется структура кучи. Здесь используется вспомогательная процедура <tex>consolidate</tex>, благодаря которой собственно и достигается желанная амортизированная оценка. В данном случае <tex> min = \varnothing</tex> не рассматривается и считается нарушением предусловий <tex>deleteMin</tex> | ||
| + | <code style="display:inline-block"> | ||
| + | '''int''' deleteMin: | ||
| + | '''Node''' prevMin = min | ||
| + | unionLists(min, min.child) <span style="color:#008000"> // список детей min объединяем с корневым</span> | ||
| + | '''Node''' L = min.left <span style="color:#008000"> // аккуратно удаляем min из списка</span> | ||
| + | '''Node''' R = min.right | ||
| + | L.right = R | ||
| + | R.left = L | ||
| + | '''if''' prevMin.right = prevMin <span style="color:#008000"> // отдельно рассмотрим случай с одним элементом</span> | ||
| + | min <tex>= \varnothing</tex> | ||
| + | '''return''' | ||
| + | min = min.right <span style="color:#008000"> // пока что перекинем указатель min на правого сына, а далее consolidate() скорректирует min в процессе выполнения</span> | ||
| + | consolidate() | ||
| + | size-- | ||
| + | '''return''' prevMin.key | ||
| + | </code> | ||
| + | ===== Прорежение деревьев ===== | ||
| + | Данная процедура принимает кучу и преобразует ее таким образом, что в корневом списке остается не более <tex> degree(H) + 1</tex> вершин. | ||
| + | |||
| + | Для этого возьмем массив списков указателей на корни деревьев <tex> A[0 \dots D[H]] </tex>, где <tex> degree(H) </tex> {{---}} максимальная степень вершины в текущем корневом списке. | ||
| + | |||
| + | Затем происходит [[Биномиальная_куча#merge | процесс, аналогичный слиянию биномиальных куч]]: добавляем поочередно каждый корень, смотря на его степень. Пусть она равна <tex> d </tex>. Если в соответствующей ячейке <tex>A</tex> еще нету вершины, записываем текущую вершину туда. Иначе подвешиваем одно дерево к другому, и пытаемся также добавить дерево, степень корня которого уже равна <tex> d + 1 </tex>. Продолжаем, пока не найдем свободную ячейку. Подвешиваем мы его следующим образом: в корневой список добавляем корень минимальный из тех двух, а корень другого добавляем в список детей корневой вершины. Чтобы лучше понять этот процесс лучше воспользоваться [https://www.cs.usfca.edu/~galles/visualization/FibonacciHeap.html визуализатором] | ||
| + | <code style="display:inline-block"> | ||
| + | '''function''' consolidate: | ||
| + | A = '''Node[]''' | ||
| + | A[min.degree] = min <span style="color:#008000"> // создаем массив и инициализируем его min</span> | ||
| + | '''Node''' current = min.right | ||
| + | '''while''' A[current.degree] <tex>\neq</tex> current<span style="color:#008000"> // пока элементы массива меняются</span> | ||
| + | '''if''' A[current.degree] <tex>= \varnothing</tex> <span style="color:#008000"> // если ячейка пустая, то положим в нее текущий элемент</span> | ||
| + | A[current.degree] = current | ||
| + | current = current.right | ||
| + | '''else''' <span style="color:#008000"> // иначе подвесим к меньшему из текущего корня и того, который лежит в ячейке другой</span> | ||
| + | '''Node''' conflict = A[current.degree] | ||
| + | '''Node''' addTo, adding | ||
| + | '''if''' conflict.key < current.key | ||
| + | addTo = conflict | ||
| + | adding = current | ||
| + | '''else''' | ||
| + | addTo = current | ||
| + | adding = conflict | ||
| + | unionLists(addTo.child, adding) | ||
| + | adding.parent = addTo | ||
| + | addTo.degree++ | ||
| + | current = addTo | ||
| + | '''if''' min.key > current.key <span style="color:#008000"> // обновляем минимум, если нужно</span> | ||
| + | min = current | ||
| + | </code> | ||
| + | '''Пример''' | ||
| + | |||
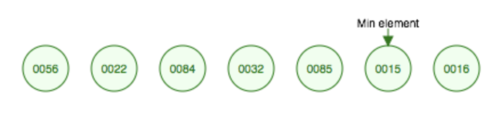
| + | Изначально добавляем в нашу кучу <tex>7</tex> элементов <tex>56, 22, 84, 32, 85, 15, 16</tex>. После этого выполним операцию извлечения минимума: | ||
| + | |||
| + | [[File:Fibonacci-heap-consolidate-example-1.png|thumb|center|500px|Начальное состояние кучи]] | ||
| + | |||
| + | |||
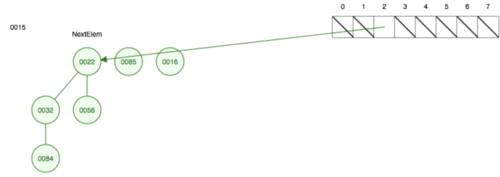
| + | * Удалим минимальный элемент из циклического корневого списка и заведем массив <tex>A</tex> для дальнейшего прорежения. | ||
| + | |||
| + | |||
| + | [[File:Fibonacci-heap-consolidate-example-2.png|thumb|center|500px|Удаление мимимума и создание массива]] | ||
| + | |||
| + | |||
| + | * Начнем процесс протяжения с первого элемента {{---}} <tex>56</tex>. Его степень равна <tex>0</tex> поэтому запишем его адрес в нулевую ячейку массива. | ||
| + | |||
| + | |||
| + | [[File:Fibonacci-heap-consolidate-example-3.png|thumb|center|500px|Состояние массива после первой итерации]] | ||
| + | |||
| + | |||
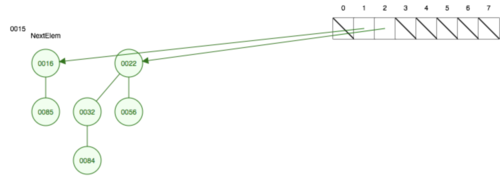
| + | * Следующий элемент <tex>22</tex> тоже имеет степень <tex>0</tex>. Возникает конфликт, который решается подвешиванием к меньшему корню большего. То есть к <tex>22</tex> подвешиваем <tex>56</tex> и увеличиваем степень <tex>22</tex> на <tex>1</tex>. В итоге степень <tex>22</tex> равна <tex>1</tex>. Записываем адрес <tex>22</tex> по индексу <tex>1</tex> в массив. | ||
| + | |||
| + | [[File:Fibonacci-heap-consolidate-example-4.png.png|thumb|center|500px|Состояние после второй итерации]] | ||
| + | |||
| + | |||
| + | * Делаем тоже самое, что и на предыдущих итерациях, но теперь объединяем <tex>32</tex> и <tex>84</tex> | ||
| + | |||
| + | |||
| + | [[File:Fibonacci-heap-consolidate-example-5.png|thumb|center|500px|Состояние после четвертой итерации]] | ||
| + | |||
| + | |||
| + | * Теперь у нас два элемента со степенью <tex>1</tex> в корневом списке. Объединим их подвесив к меньшему корню {{---}} <tex>22</tex>, больший {{---}} <tex>32</tex>. Теперь степень <tex>22</tex> равна <tex>2</tex>, запишем на <tex>2</tex> позицию массива обновленное значение. | ||
| + | |||
| + | |||
| + | [[File:Fibonacci-heap-consolidate-example-6.png|thumb|center|500px|Состояние после пятой итерации]] | ||
| + | |||
| + | |||
| + | * Ну и наконец аналогично объедений последние два элемента. | ||
| + | |||
| + | |||
| + | [[File:Fibonacci-heap-consolidate-example-7.png|thumb|center|500px|Финальное состояние кучи]] | ||
| + | |||
| + | ==== Уменьшение значения элемента ==== | ||
| + | Основная идея: хотим, чтобы учетная стоимость данной операции была <tex> O(1) </tex>. Было бы хорошо, чтобы вершина не всплывала до корня, и тогда дерево не придется сильно перестраивать. Для этого при удобном случае будем вырезать поддерево полностью и перемещать его в корневой [[Список |список]]. Итак, сам алгоритм: | ||
| + | |||
| + | # Проверяем, если новое значение ключа все же не меньше значения ключа родителя, то все хорошо, и мы выходим. | ||
| + | # Иначе, вырезаем дерево с текущей вершиной в корневой [[Список |список]], и производим каскадное вырезание родителя. | ||
| + | <code style="display:inline-block"> | ||
| + | '''function''' decreaseKey(x: '''Node''', newValue: '''int'''): | ||
| + | '''if''' newValue > x.parent.key <span style="color:#008000"> // если после изменения структура дерева сохранится, то меняем и выходим</span> | ||
| + | x.key = newValue | ||
| + | '''return''' | ||
| + | '''Node''' parent = x.parent <span style="color:#008000"> // иначе вызываем cut и cascadingCut</span> | ||
| + | cut(x) | ||
| + | cascadingCut(parent) | ||
| + | </code> | ||
| + | ===== Вырезание ===== | ||
| + | При вырезании вершины мы удаляем ее из списка детей своего родителя, уменьшаем степень ее родителя (<tex> x.p.degree </tex>) и снимаем пометку с текущей вершины (<tex> x.mark = false </tex>). | ||
| + | <code style="display:inline-block"> | ||
| + | '''function''' cut(x: '''Node''') | ||
| + | '''Node''' L = x.left | ||
| + | '''Node''' R = x.right | ||
| + | R.left = L <span style="color:#008000"> // аккуратно удаляем текущую вершину</span> | ||
| + | L.right = R | ||
| + | x.parent.degree-- | ||
| + | '''if''' x.parent.child = x <span style="color:#008000"> // чтобы родитель не потерял ссылку на сыновей проверяем: </span> | ||
| + | '''if''' x.right = x. <span style="color:#008000"> // если узел который мы вырезаем содержится в родителе, то меняем его на соседний</span> | ||
| + | x.parent.child <tex>= \varnothing</tex> <span style="color:#008000"> // иначе у родителя больше нет детей</span> | ||
| + | '''else''' | ||
| + | x.parent.child = x.right | ||
| + | x.right = x | ||
| + | x.left = x | ||
| + | x.parent <tex>= \varnothing</tex> | ||
| + | unionLists(min, x) <span style="color:#008000"> // вставляем наше поддерево в корневой список</span> | ||
| + | </code> | ||
| + | |||
| + | ===== Каскадное вырезание ===== | ||
| + | Перед вызовом каскадного вырезания нам известно, удаляли ли ребенка у этой вершины. Если у вершины до этого не удаляли дочерний узел (<tex> x.mark = false </tex>), то мы помечаем эту вершину (<tex> x.mark = true </tex>) и прекращаем выполнение операции. В противном случае применяем операцию <tex>\mathrm {cut}</tex> для текущей вершины и запускаем каскадное вырезание от родителя. | ||
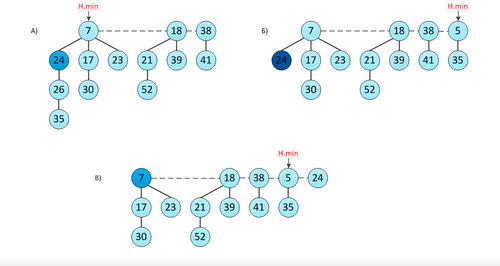
| + | [[File:Каскадное вырезание.png|thumb|500px|Пример каскадного вырезания]] | ||
| + | <code style="display:inline-block"> | ||
| + | '''function''' cascadingCut(x: '''Node''') | ||
| + | '''while''' x.mark = '''true''' <span style="color:#008000"> // пока у нас помеченые вершины вырезаем их</span> | ||
| + | cut(x) | ||
| + | x = x.parent | ||
| + | x.mark = true <span style="color:#008000"> // последнюю вершину нужно пометить {{---}} у нее удаляли ребенка</span> | ||
| + | </code> | ||
| + | |||
| + | '''Пример''' | ||
| + | |||
| + | Рисунок иллюстрирует пример каскадного вырезания: | ||
| + | |||
| + | * Изначально, куча состояла из <tex>3</tex> фибоначчиевых деревьев. У вершины с ключом <tex>24</tex> отсутствует <tex>1</tex> ребенок. | ||
| + | * Уменьшаем ключ <tex>26</tex> до <tex>5</tex> и делаем операцию <tex>\mathrm {cut}</tex> этого дерева. Получаем кучу с <tex>4</tex> деревьями и новым минимумом. Но у вершины с ключом <tex>24</tex> был удален второй ребенок, поэтому запускам операцию <tex>\mathrm {cascadingCut}</tex> для этой вершины: вырезаем ее, помещаем в корневой [[Список |список]] и помечаем ее родителя. | ||
| + | * У вершины с ключом <tex>7</tex> удален лишь один ребенок, поэтому операция <tex>\mathrm {cascadingCut}</tex> от нее не запускается. В итоге, получаем кучу, состоящую из <tex>5</tex> фибоначчиевых деревьев. | ||
| + | |||
| + | ==== Удаление элемента ==== | ||
| + | Удаление вершины реализуется через уменьшение ее ключа до <tex> -\infty </tex> и последующим извлечением минимума. | ||
| + | <code style="display:inline-block"> | ||
| + | '''function''' delete(x: '''Node''') | ||
| + | decreaseKey(x, <tex>-\infty</tex>) | ||
| + | deleteMin() | ||
| + | </code> | ||
| + | |||
| + | == Время работы == | ||
| + | ==== Потенциал ==== | ||
| + | Для анализа производительности операций введем потенциал для фибоначчиевой кучи как <tex> \Phi = trees + 2 * marked </tex>, где <tex> trees </tex> {{---}} количество элементов в корневом списке кучи, а <tex> marked </tex> {{---}} количество вершин, у которых удален один ребенок (то есть вершин с пометкой <tex> x.mark = true </tex>). Договоримся, что единицы потенциала достаточно для оплаты константного количества работы. | ||
| + | ==== Cоздание кучи ==== | ||
| + | Очевидно, что реальное время работы {{---}} <tex> O(1) </tex>. | ||
| + | ==== Вставка элемента ==== | ||
| + | Для оценки амортизированной стоимости операции рассмотрим исходную кучу <tex> H </tex> и получившуюся в результате вставки нового элемента кучу <tex> H' </tex>. <tex> trees(H') = trees(H) + 1 </tex> и <tex> marked(H') = marked(H) </tex>. Следовательно, увеличение потенциала составляет <tex> (trees(H) + 1 + 2 * marked(H)) - (trees(H) + 2 * marked(H)) = 1 </tex>. Так как реальное время работы составляет <tex> O(1) </tex>, то амортизированная стоимость данной операции также равна <tex> O(1) </tex>. | ||
| + | ==== Получение минимального элемента ==== | ||
| + | Истинное время работы {{---}} <tex> O(1) </tex>. | ||
| + | ==== Соедининение двух куч ==== | ||
| + | Реальное время работы {{---}} <tex> O(1) </tex>. Амортизированное время работы также <tex> O(1) </tex>, поскольку, при объединении двух куч в одну, потенциалы обеих куч суммируются, итоговая сумма потенциалов не изменяется, <tex> \Phi_{n + 1} - \Phi_n = 0 </tex>. | ||
| + | ==== Удаление минимального элемента==== | ||
| + | Для доказательства времени работы этого алгоритма нам понадобится доказать несколько вспомогательных утверждений. | ||
{{Лемма | {{Лемма | ||
|id=Лемма1 | |id=Лемма1 | ||
| Строка 38: | Строка 282: | ||
|proof= | |proof= | ||
Докажем это утверждение по индукции. | Докажем это утверждение по индукции. | ||
| − | Пусть <tex>s_n</tex> {{---}} минимальный размер фибоначчиева дерева порядка n. | + | Пусть <tex>s_n</tex> {{---}} минимальный размер фибоначчиева дерева порядка <tex>n</tex>. |
При <tex>n = 0</tex> | При <tex>n = 0</tex> | ||
| Строка 53: | Строка 297: | ||
<tex>s_n = 1 + \sum\limits_{i=0}^{n-2} s_i \geqslant 1 + \sum\limits_{i=0}^{n-2} F_i</tex> | <tex>s_n = 1 + \sum\limits_{i=0}^{n-2} s_i \geqslant 1 + \sum\limits_{i=0}^{n-2} F_i</tex> | ||
| − | Но по предыдущей [[#Лемма1|лемме]] | + | Но по предыдущей [[#Лемма1|лемме]] : |
| − | |||
| − | + | <tex>1 + \sum\limits_{i=0}^{n-2} F_i = F_n</tex>. Следовательно, <tex>s_n \geqslant F_n</tex> | |
| − | |||
| − | |||
| − | |||
| − | |||
}} | }} | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
{{Лемма | {{Лемма | ||
|id=Лемма3 | |id=Лемма3 | ||
| − | |statement= <tex>F_n = | + | |statement= <tex>F_n =O(\varphi^n)</tex>, где <tex dpi="160"> \varphi = \frac {1 + \sqrt 5} {2}</tex> |
|proof= | |proof= | ||
Для начала докажем, что <tex>F_n =</tex> <tex dpi="160">\frac {\varphi^n - (-\varphi)^{-n}} {\sqrt 5}</tex> | Для начала докажем, что <tex>F_n =</tex> <tex dpi="160">\frac {\varphi^n - (-\varphi)^{-n}} {\sqrt 5}</tex> | ||
| Строка 84: | Строка 313: | ||
<tex>F_0 =</tex> <tex dpi="160">\frac {\varphi^0 - (-\varphi)^0} {\sqrt 5} = \frac {1 - 1} {\sqrt 5} = 0</tex>, что верно. | <tex>F_0 =</tex> <tex dpi="160">\frac {\varphi^0 - (-\varphi)^0} {\sqrt 5} = \frac {1 - 1} {\sqrt 5} = 0</tex>, что верно. | ||
| − | При <tex> | + | При <tex>n = 1</tex> |
<tex>F_1 =</tex> <tex dpi="160">\frac {\varphi^1 - (-\varphi)^{-1}} {\sqrt 5} = \frac {1} {\sqrt 5}(\frac {1 + \sqrt 5} {2} - \frac {1 - \sqrt 5} {2}) = \frac {2\sqrt 5} {2\sqrt 5} = 1</tex>, что также верно. | <tex>F_1 =</tex> <tex dpi="160">\frac {\varphi^1 - (-\varphi)^{-1}} {\sqrt 5} = \frac {1} {\sqrt 5}(\frac {1 + \sqrt 5} {2} - \frac {1 - \sqrt 5} {2}) = \frac {2\sqrt 5} {2\sqrt 5} = 1</tex>, что также верно. | ||
| Строка 96: | Строка 325: | ||
Подставив вместо <tex>\varphi</tex> его значение, нетрудно убедится, что <tex>\varphi^{-1} + \varphi^{-2} = -\varphi + \varphi^{2} = 1</tex> | Подставив вместо <tex>\varphi</tex> его значение, нетрудно убедится, что <tex>\varphi^{-1} + \varphi^{-2} = -\varphi + \varphi^{2} = 1</tex> | ||
| − | Поскольку <tex>\left\vert (-\varphi)^{-1} \right\vert < 1</tex>, то выполняются неравенства <tex dpi="160">\frac {(-\varphi)^{-n}} {\sqrt 5} < \frac {1} {\sqrt 5} < \frac {1} {2}</tex>. Таким образом, <tex>n</tex>- | + | Поскольку <tex>\left\vert (-\varphi)^{-1} \right\vert < 1</tex>, то выполняются неравенства <tex dpi="160">\frac {(-\varphi)^{-n}} {\sqrt 5} < \frac {1} {\sqrt 5} < \frac {1} {2}</tex>. Таким образом, <tex>n</tex>-ое число Фибоначчи равно <tex dpi="160">\frac {\varphi^{n}} {\sqrt 5}</tex>, округленному до ближайшего целого числа. Следовательно, <tex>F_n =O(\varphi^n)</tex>. |
}} | }} | ||
| Строка 102: | Строка 331: | ||
{{Лемма | {{Лемма | ||
|id=Лемма4 | |id=Лемма4 | ||
| − | |statement=Максимальная степень <tex> | + | |statement=Максимальная степень <tex>degree</tex> произвольной вершины в фибоначчиевой куче с <tex>n</tex> вершинами равна <tex>O(\log n)</tex> |
|proof= | |proof= | ||
| − | Пусть <tex>x</tex> {{---}} произвольная вершина в фибоначчиевой куче с <tex>n</tex> вершинами, и пусть <tex>k</tex> {{---}} степень вершины <tex>x</tex>. Тогда по [[#Лемма2|доказанному выше]] в дереве, корень которого <tex>x</tex>, содержится не менее <tex>F_k</tex> вершин, что в свою очередь по [[#Лемма3|лемме]] равно <tex> | + | Пусть <tex>x</tex> {{---}} произвольная вершина в фибоначчиевой куче с <tex>n</tex> вершинами, и пусть <tex>k</tex> {{---}} степень вершины <tex>x</tex>. Тогда по [[#Лемма2|доказанному выше]] в дереве, корень которого <tex>x</tex>, содержится не менее <tex>F_k</tex> вершин, что в свою очередь по [[#Лемма3|лемме]] равно <tex>O(\varphi^k)</tex>. |
То есть | То есть | ||
| Строка 113: | Строка 342: | ||
<tex>\log_{\varphi}n \geqslant k</tex> | <tex>\log_{\varphi}n \geqslant k</tex> | ||
| − | Таким образом, максимальная степень <tex> | + | Таким образом, максимальная степень <tex>degree</tex> произвольной вершины равна <tex>O(\log n)</tex>. |
}} | }} | ||
| − | + | Итоговая асимптотика операции <tex>\mathrm {extraxtMin}</tex>, учитывая и вспомогательную функцию <tex> \mathrm {consolidate} </tex>, время работы которой доказывается ниже, равно: <tex> O(1)+O(degree)+O(degree)=O(degree) </tex>. По доказанной выше [[#Лемма4|лемме]] <tex>O(degree) = O(\log(n))</tex>. | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | Учетная стоимость <tex> \mathrm {consolidate} </tex> равна <tex> O(degree) </tex>. Докажем это: | |
| − | + | Изначально в корневом списке было не более <tex> degree + trees - 1 </tex> вершин, поскольку он состоит из исходного списка корней с <tex>trees</tex> узлами, минус извлеченный узел и плюс дочерние узлы, количество которых не превышает <tex> degree </tex>. В ходе операции <tex> \mathrm {consolidate} </tex> мы сделали <tex> O(degree + trees) </tex> слияний деревьев. Потенциал перед извлечением минимума равен <tex> trees + 2 * marked </tex>, а после не превышает <tex> degree + 1 + 2 * marked</tex>, поскольку в корневом списке остается не более <tex> degree + 1 </tex> узлов, а количество помеченных узлов не изменяется. Таким образом, амортизированная стоимость не превосходит | |
| − | + | <tex> O(degree + trees) + (degree + 1 + 2 * marked) - (trees + 2 * marked) = O(degree) + O(trees) - trees</tex> | |
| − | + | Поскольку мы договорились, что можем масштабировать единицу потенциала таким образом, чтобы покрывать константное количество работы, то итоговая амортизационная оценка {{---}} <tex> O(degree) </tex> | |
| + | ==== Уменьшение значения элемента ==== | ||
| + | Докажем, что амортизированное время работы операции <tex> \mathrm {decreaseKey} </tex> есть <tex> O(1) </tex>. Поскольку в процедуре нет циклов, ее время работы определяется лишь количеством рекурсивных вызовов каскадного вырезания. | ||
| − | + | Пусть мы вызвали процедуру каскадного вырезания подверглось <tex> k </tex> раз. Так как реальное время работы каждой итерации <tex> \mathrm {cascadingCut} </tex> составляет <tex> O(1) </tex>, то реальное время работы операции <tex> \mathrm {decreaseKey} </tex> {{---}} <tex> O(k) </tex>. | |
| − | = | + | Рассмотрим, как изменится потенциал в результате выполнения данной операции. Пусть <tex> H </tex> {{---}} фибоначчиева куча до вызова <tex> \mathrm {decreaseKey} </tex>. Тогда после <tex> k </tex> итераций операции <tex> \mathrm {cascadingCut} </tex> вершин с пометкой <tex> x.mark = true </tex> стало как минимум на <tex> k - 2 </tex> меньше, потому что каждый вызов каскадного вырезания, за исключением последнего, уменьшает количество помеченных вершин на одну, и в результате последнего вызова одну вершину мы можем пометить. В корневом списке прибавилось <tex> k </tex> новых деревьев (<tex> k - 1 </tex> дерево за счет каскадного вырезания и еще одно из-за самого первого вызова операции <tex> \mathrm {cut} </tex>). |
| − | + | В итоге, изменение потенциала составляет: <tex> \Phi_i - \Phi_{i - 1} = ((trees + k) + 2 * (marked + k - 2)) - (trees + 2 * marked) = 4 - k </tex>. Следовательно, амортизированная стоимость не превышает <tex> O(k) + 4 - k </tex>. Но поскольку мы можем соответствующим образом масштабировать единицы потенциала, то амортизированная стоимость операции <tex> \mathrm {decreaseKey} </tex> равна <tex> O(1) </tex>. | |
| + | ==== Удаление элемента ==== | ||
| + | Амортизированное время работы: <tex> O(1) + O(degree) = O(degree) </tex>. | ||
| − | Поскольку ранее мы показали, что <tex> | + | Поскольку ранее мы показали, что <tex> degree = O(\log n ) </tex>, то соответствующие оценки доказаны. |
| + | ==== Итоговая таблица ==== | ||
| + | {| style="background-color:#CCC;margin:0.5px" | ||
| + | !style="background-color:#EEE"| Операция | ||
| + | !style="background-color:#EEE"| Амортизированная сложность | ||
| + | |-align="center" | ||
| + | |style="background-color:#FFF;padding:2px 10px"| <tex>\mathrm {makeHeap}</tex> | ||
| + | |style="background-color:#FFF;padding:2px 10px"| <tex>O(1)</tex> | ||
| + | |-align="center" | ||
| + | |style="background-color:#FFF;padding:2px 10px"| <tex>\mathrm {insert}</tex> | ||
| + | |style="background-color:#FFF;padding:2px 10px"| <tex>O(1)</tex> | ||
| + | |-align="center" | ||
| + | |style="background-color:#FFF;padding:2px 10px"| <tex>\mathrm {getMin}</tex> | ||
| + | |style="background-color:#FFF;padding:2px 10px"| <tex>O(1)</tex> | ||
| + | |-align="center" | ||
| + | |style="background-color:#FFF;padding:2px 10px"| <tex>\mathrm {merge}</tex> | ||
| + | |style="background-color:#FFF;padding:2px 10px"| <tex>O(1)</tex> | ||
| + | |-align="center" | ||
| + | |style="background-color:#FFF;padding:2px 10px"| <tex>\mathrm {extractMin}</tex> | ||
| + | |style="background-color:#FFF;padding:2px 10px"| <tex>O(\log n )</tex> | ||
| + | |-align="center" | ||
| + | |style="background-color:#FFF;padding:2px 10px"| <tex>\mathrm {decreaseKey}</tex> | ||
| + | |style="background-color:#FFF;padding:2px 10px"| <tex>O(1)</tex> | ||
| + | |-align="center" | ||
| + | |style="background-color:#FFF;padding:2px 10px"| <tex>\mathrm {delete}</tex> | ||
| + | |style="background-color:#FFF;padding:2px 10px"| <tex>O(\log n )</tex> | ||
| + | |} | ||
| − | = | + | == Недостатки и достоинства == |
| + | '''Недостатки''': | ||
| + | * Большое потребление памяти на узел(минимум 21 байт) | ||
| + | * Большая константа времени работы, что делает ее малоприменимой для реальных задач | ||
| + | * Некоторые операции в худшем случае могут работать за <tex>O(n)</tex> времени | ||
| + | '''Достоинства''': | ||
| + | * Одно из лучших асимптотических времен работы для всех операций | ||
| + | == См. также == | ||
| + | * [[Приоритетные очереди]] | ||
| + | * [[Двоичная куча]] | ||
| + | * [[Биномиальная куча]] | ||
| + | * [[Левосторонняя куча]] | ||
| + | * [[Тонкая куча]] | ||
| + | * [[Толстая куча на избыточном счетчике]] | ||
| + | * [[Куча Бродала-Окасаки]] | ||
| + | == Примечания == | ||
| + | <references/> | ||
| + | == Источники информации == | ||
* Томас Кормен, Чарльз Лейзерсон, Рональд Ривест, Клиффорд Штайн — Алгоритмы: построение и анализ. — М.: Издательский дом «Вильямс», 2005. — С. 1296. — ISBN 5-8459-0857-4 | * Томас Кормен, Чарльз Лейзерсон, Рональд Ривест, Клиффорд Штайн — Алгоритмы: построение и анализ. — М.: Издательский дом «Вильямс», 2005. — С. 1296. — ISBN 5-8459-0857-4 | ||
| − | * [ | + | * [[wikipedia:en:Числа Фибоначчи|Числа Фибоначчи {{---}} Википедия]] |
| − | * [ | + | * [[wikipedia:en:Fibonacci heap|Фибоначчиева куча {{---}} Википедия]] |
| + | * [https://www.cs.usfca.edu/~galles/visualization/FibonacciHeap.html Fibonacci heap visualization] | ||
* [http://www.intuit.ru/department/algorithms/dscm/7/2.html Фибоначчиевы кучи — INTUIT.ru] | * [http://www.intuit.ru/department/algorithms/dscm/7/2.html Фибоначчиевы кучи — INTUIT.ru] | ||
| − | * [http:// | + | * [http://www.cs.duke.edu/courses/fall05/cps230/L-11.pdf Fibonacci Heaps {{---}} Duke University] |
| − | * [ | + | * [https://www.cs.princeton.edu/~wayne/teaching/fibonacci-heap.pdf Fibonacci Heaps {{---}} Princeton University] |
| − | [[Категория: | + | [[Категория: Алгоритмы и структуры данных]] |
| + | [[Категория: Приоритетные очереди]] | ||
Текущая версия на 19:39, 4 сентября 2022
Фибоначчиева куча (англ. Fibonacci heap) — структура данных, отвечающая интерфейсу приоритетная очередь. Эта структура данных имеет меньшую амортизированную сложность, чем такие приоритетные очереди как биномиальная куча и двоичная куча. Изначально эта структура данных была разработана Майклом Фридманом[1] и Робертом Тарьяном[2] при работе по улучшению асимптотической сложности алгоритма Дейкстры. Свое название Фибоначчиева куча получила из-за использования некоторых свойств чисел Фибоначчи[3] в потенциальном анализе этой реализации.
Содержание
Структура
Фибоначчиева куча — набор из подвешенных деревьев удовлетворяющих свойству: каждый предок не больше своих детей(если дерево на минимум). Это означает, что минимум всей кучи это один из корней этих деревьев. Одно из главных преимуществ Фибоначчиевой кучи — гибкость её структуры из-за того, что на деревья не наложены никакие ограничения по форме. Например, Фибоначчиева куча может состоять хоть из деревьев в каждом из которых по одному элементу. Такая гибкость позволяет выполнять некоторые операции лениво, оставляя работу более поздним операциям. Далее будут даны некоторые определения, которые понадобятся в дальнейшем.
| Определение: |
| Степень вершины (англ. degree) — количество детей данной вершины. Далее будем обозначать как , где это вершина. |
| Определение: |
| Степень кучи (англ. degree) — наибольшая степень вершины этой кучи. Далее будем обозначать как , где это куча. |
Реализация
Для возможности быстрого удаления элемента из произвольного места и объединением с другим списком будем хранить их в циклическом двусвязном списке. Также будем хранить и все уровни поддерева. Исходя из этого структура каждого узла будет выглядеть вот так.
struct Node int key // ключ Node parent // указатель на родительский узел Node child // указатель на один из дочерних узлов Node left // указатель на левый узел того же предка Node right // указатель на правый узел того же предка int degree // степень вершины boolean mark // был ли удален в процессе изменения ключа ребенок этой вершины)
Также стоит упомянуть, что нам нужен указатель только на одного ребенка, поскольку остальные хранятся в двусвязном списке с ним. Для доступа ко всей куче нам тоже нужен всего один элемент, поэтому разумно хранить именно указатель на минимум кучи (он обязательно один из корней), а для получения размера за константное время будем хранить размер кучи отдельно.
struct fibonacciHeap int size // текущее количество узлов Node min // указатель на корень дерева с минимальным ключом
Cоздание кучи
Инициализация кучи.
function buildHeap:
min
size = 0
Вставка элемента
Данная операция вставляет новый элемент в список корней правее минимума и при необходимости меняет указатель на минимум кучи.
function insert(x: int): Node newNode // создаем новый узел newNode.key = x // инициализируем ключ нового узла if size = 0 // если куче нет элементов, то только что добавленный минимальный min = newNode min.left = newNode min.right = newNode else // иначе аккуратно меняем указатели в списке, чтобы не перепутать указатели Node prevRight = min.right min.right = newNode newNode.left = min newNode.right = prevRight prevRight.left = newNode if newNode.key < min.key min = newNode // меняем указатель на минимум, если надо newNode.parent size++ // не забываем увеличить переменную size
Получение минимального элемента
Получение минимума всей кучи.
int getMin: return min.key
Соедининение двух куч
Для сливания двух Фибоначчиевых куч необходимо просто объединить их корневые списки, а также обновить минимум новой кучи, если понадобится. Вынесем в вспомогательную функцию логику, объединяющую два списка вершины, которых подаются ей в качестве аргументов.
function unionLists(first: Node, second: Node):
Node L = first.left // аккуратно меняем указатели местами указатели
Node R = second.right
second.right = first
first.left = second
L.right = R
R.left = L
Сливаем два корневых списка в один и обновляем минимум, если нужно.
function merge(that: fibonacciHeap): if that.size = 0 // если вторая куча пуста, нечего добавлять return if size = 0 // если наша куча пуста, то результатом будет вторая куча min = that.min size = that.size else unionLists(min, that.min) // объединяем два корневых списка size += that.size if min or (that.min and that.min < min) // если минимум кучи изменился, то надо обновить указатель min = that.min
Удаление минимального элемента
Первая рассматриваемая операция, в ходе которой значительно меняется структура кучи. Здесь используется вспомогательная процедура , благодаря которой собственно и достигается желанная амортизированная оценка. В данном случае не рассматривается и считается нарушением предусловий
int deleteMin: Node prevMin = min unionLists(min, min.child) // список детей min объединяем с корневым Node L = min.left // аккуратно удаляем min из списка Node R = min.right L.right = R R.left = L if prevMin.right = prevMin // отдельно рассмотрим случай с одним элементом min return min = min.right // пока что перекинем указатель min на правого сына, а далее consolidate() скорректирует min в процессе выполнения consolidate() size-- return prevMin.key
Прорежение деревьев
Данная процедура принимает кучу и преобразует ее таким образом, что в корневом списке остается не более вершин.
Для этого возьмем массив списков указателей на корни деревьев , где — максимальная степень вершины в текущем корневом списке.
Затем происходит процесс, аналогичный слиянию биномиальных куч: добавляем поочередно каждый корень, смотря на его степень. Пусть она равна . Если в соответствующей ячейке еще нету вершины, записываем текущую вершину туда. Иначе подвешиваем одно дерево к другому, и пытаемся также добавить дерево, степень корня которого уже равна . Продолжаем, пока не найдем свободную ячейку. Подвешиваем мы его следующим образом: в корневой список добавляем корень минимальный из тех двух, а корень другого добавляем в список детей корневой вершины. Чтобы лучше понять этот процесс лучше воспользоваться визуализатором
function consolidate: A = Node[] A[min.degree] = min // создаем массив и инициализируем его min Node current = min.right while A[current.degree] current // пока элементы массива меняются if A[current.degree] // если ячейка пустая, то положим в нее текущий элемент A[current.degree] = current current = current.right else // иначе подвесим к меньшему из текущего корня и того, который лежит в ячейке другой Node conflict = A[current.degree] Node addTo, adding if conflict.key < current.key addTo = conflict adding = current else addTo = current adding = conflict unionLists(addTo.child, adding) adding.parent = addTo addTo.degree++ current = addTo if min.key > current.key // обновляем минимум, если нужно min = current
Пример
Изначально добавляем в нашу кучу элементов . После этого выполним операцию извлечения минимума:
- Удалим минимальный элемент из циклического корневого списка и заведем массив для дальнейшего прорежения.
- Начнем процесс протяжения с первого элемента — . Его степень равна поэтому запишем его адрес в нулевую ячейку массива.
- Следующий элемент тоже имеет степень . Возникает конфликт, который решается подвешиванием к меньшему корню большего. То есть к подвешиваем и увеличиваем степень на . В итоге степень равна . Записываем адрес по индексу в массив.
- Делаем тоже самое, что и на предыдущих итерациях, но теперь объединяем и
- Теперь у нас два элемента со степенью в корневом списке. Объединим их подвесив к меньшему корню — , больший — . Теперь степень равна , запишем на позицию массива обновленное значение.
- Ну и наконец аналогично объедений последние два элемента.
Уменьшение значения элемента
Основная идея: хотим, чтобы учетная стоимость данной операции была . Было бы хорошо, чтобы вершина не всплывала до корня, и тогда дерево не придется сильно перестраивать. Для этого при удобном случае будем вырезать поддерево полностью и перемещать его в корневой список. Итак, сам алгоритм:
- Проверяем, если новое значение ключа все же не меньше значения ключа родителя, то все хорошо, и мы выходим.
- Иначе, вырезаем дерево с текущей вершиной в корневой список, и производим каскадное вырезание родителя.
function decreaseKey(x: Node, newValue: int): if newValue > x.parent.key // если после изменения структура дерева сохранится, то меняем и выходим x.key = newValue return Node parent = x.parent // иначе вызываем cut и cascadingCut cut(x) cascadingCut(parent)
Вырезание
При вырезании вершины мы удаляем ее из списка детей своего родителя, уменьшаем степень ее родителя () и снимаем пометку с текущей вершины ().
function cut(x: Node) Node L = x.left Node R = x.right R.left = L // аккуратно удаляем текущую вершину L.right = R x.parent.degree-- if x.parent.child = x // чтобы родитель не потерял ссылку на сыновей проверяем: if x.right = x. // если узел который мы вырезаем содержится в родителе, то меняем его на соседний x.parent.child // иначе у родителя больше нет детей else x.parent.child = x.right x.right = x x.left = x x.parent unionLists(min, x) // вставляем наше поддерево в корневой список
Каскадное вырезание
Перед вызовом каскадного вырезания нам известно, удаляли ли ребенка у этой вершины. Если у вершины до этого не удаляли дочерний узел (), то мы помечаем эту вершину () и прекращаем выполнение операции. В противном случае применяем операцию для текущей вершины и запускаем каскадное вырезание от родителя.
function cascadingCut(x: Node) while x.mark = true // пока у нас помеченые вершины вырезаем их cut(x) x = x.parent x.mark = true // последнюю вершину нужно пометить — у нее удаляли ребенка
Пример
Рисунок иллюстрирует пример каскадного вырезания:
- Изначально, куча состояла из фибоначчиевых деревьев. У вершины с ключом отсутствует ребенок.
- Уменьшаем ключ до и делаем операцию этого дерева. Получаем кучу с деревьями и новым минимумом. Но у вершины с ключом был удален второй ребенок, поэтому запускам операцию для этой вершины: вырезаем ее, помещаем в корневой список и помечаем ее родителя.
- У вершины с ключом удален лишь один ребенок, поэтому операция от нее не запускается. В итоге, получаем кучу, состоящую из фибоначчиевых деревьев.
Удаление элемента
Удаление вершины реализуется через уменьшение ее ключа до и последующим извлечением минимума.
function delete(x: Node)
decreaseKey(x, )
deleteMin()
Время работы
Потенциал
Для анализа производительности операций введем потенциал для фибоначчиевой кучи как , где — количество элементов в корневом списке кучи, а — количество вершин, у которых удален один ребенок (то есть вершин с пометкой ). Договоримся, что единицы потенциала достаточно для оплаты константного количества работы.
Cоздание кучи
Очевидно, что реальное время работы — .
Вставка элемента
Для оценки амортизированной стоимости операции рассмотрим исходную кучу и получившуюся в результате вставки нового элемента кучу . и . Следовательно, увеличение потенциала составляет . Так как реальное время работы составляет , то амортизированная стоимость данной операции также равна .
Получение минимального элемента
Истинное время работы — .
Соедининение двух куч
Реальное время работы — . Амортизированное время работы также , поскольку, при объединении двух куч в одну, потенциалы обеих куч суммируются, итоговая сумма потенциалов не изменяется, .
Удаление минимального элемента
Для доказательства времени работы этого алгоритма нам понадобится доказать несколько вспомогательных утверждений.
| Лемма: |
Для всех целых
, где — -ое число Фибоначчи, определяемое формулой: |
| Доказательство: |
|
Докажем лемму по индукции: при , что действительно верно. По индукции предполагаем, что . Тогда |
| Лемма: |
Фибоначчиево дерево порядка содержит не менее вершин. |
| Доказательство: |
|
Докажем это утверждение по индукции. Пусть — минимальный размер фибоначчиева дерева порядка . При . При . Предположим по индукции, что для всех . Пусть в нашем дереве удалено поддерево порядка . Тогда
Но по предыдущей лемме : . Следовательно, |
| Лемма: |
, где |
| Доказательство: |
|
Для начала докажем, что Используем для этого математическую индукцию. При , что верно. При , что также верно. По индукции предполагаем, что и . Тогда
Подставив вместо его значение, нетрудно убедится, что Поскольку , то выполняются неравенства . Таким образом, -ое число Фибоначчи равно , округленному до ближайшего целого числа. Следовательно, . |
| Лемма: |
Максимальная степень произвольной вершины в фибоначчиевой куче с вершинами равна |
| Доказательство: |
|
Пусть — произвольная вершина в фибоначчиевой куче с вершинами, и пусть — степень вершины . Тогда по доказанному выше в дереве, корень которого , содержится не менее вершин, что в свою очередь по лемме равно . То есть
Логарифмируя по основанию , получаем Таким образом, максимальная степень произвольной вершины равна . |
Итоговая асимптотика операции , учитывая и вспомогательную функцию , время работы которой доказывается ниже, равно: . По доказанной выше лемме .
Учетная стоимость равна . Докажем это:
Изначально в корневом списке было не более вершин, поскольку он состоит из исходного списка корней с узлами, минус извлеченный узел и плюс дочерние узлы, количество которых не превышает . В ходе операции мы сделали слияний деревьев. Потенциал перед извлечением минимума равен , а после не превышает , поскольку в корневом списке остается не более узлов, а количество помеченных узлов не изменяется. Таким образом, амортизированная стоимость не превосходит
Поскольку мы договорились, что можем масштабировать единицу потенциала таким образом, чтобы покрывать константное количество работы, то итоговая амортизационная оценка —
Уменьшение значения элемента
Докажем, что амортизированное время работы операции есть . Поскольку в процедуре нет циклов, ее время работы определяется лишь количеством рекурсивных вызовов каскадного вырезания.
Пусть мы вызвали процедуру каскадного вырезания подверглось раз. Так как реальное время работы каждой итерации составляет , то реальное время работы операции — .
Рассмотрим, как изменится потенциал в результате выполнения данной операции. Пусть — фибоначчиева куча до вызова . Тогда после итераций операции вершин с пометкой стало как минимум на меньше, потому что каждый вызов каскадного вырезания, за исключением последнего, уменьшает количество помеченных вершин на одну, и в результате последнего вызова одну вершину мы можем пометить. В корневом списке прибавилось новых деревьев ( дерево за счет каскадного вырезания и еще одно из-за самого первого вызова операции ).
В итоге, изменение потенциала составляет: . Следовательно, амортизированная стоимость не превышает . Но поскольку мы можем соответствующим образом масштабировать единицы потенциала, то амортизированная стоимость операции равна .
Удаление элемента
Амортизированное время работы: .
Поскольку ранее мы показали, что , то соответствующие оценки доказаны.
Итоговая таблица
| Операция | Амортизированная сложность |
|---|---|
Недостатки и достоинства
Недостатки:
- Большое потребление памяти на узел(минимум 21 байт)
- Большая константа времени работы, что делает ее малоприменимой для реальных задач
- Некоторые операции в худшем случае могут работать за времени
Достоинства:
- Одно из лучших асимптотических времен работы для всех операций
См. также
- Приоритетные очереди
- Двоичная куча
- Биномиальная куча
- Левосторонняя куча
- Тонкая куча
- Толстая куча на избыточном счетчике
- Куча Бродала-Окасаки
Примечания
Источники информации
- Томас Кормен, Чарльз Лейзерсон, Рональд Ривест, Клиффорд Штайн — Алгоритмы: построение и анализ. — М.: Издательский дом «Вильямс», 2005. — С. 1296. — ISBN 5-8459-0857-4
- Числа Фибоначчи — Википедия
- Фибоначчиева куча — Википедия
- Fibonacci heap visualization
- Фибоначчиевы кучи — INTUIT.ru
- Fibonacci Heaps — Duke University
- Fibonacci Heaps — Princeton University