Красно-черное дерево — различия между версиями
Ministr (обсуждение | вклад) (→Вставка элемента) |
м (rollbackEdits.php mass rollback) |
||
| (не показано 148 промежуточных версий 22 участников) | |||
| Строка 1: | Строка 1: | ||
| − | + | '''Красно-чёрное дерево''' (англ. ''red-black tree'') {{---}} двоичное дерево поиска, в котором баланс осуществляется на основе "цвета" узла дерева, который принимает только два значения: "красный" (англ. ''red'') и "чёрный" (англ. ''black''). | |
| − | При этом все листья дерева являются фиктивными и не содержат данных. | + | [[Файл:RBT.jpg|350px|thumb|Пример красно-чёрного дерева.]] |
| + | При этом все листья дерева являются фиктивными и не содержат данных, но относятся к дереву и являются чёрными. | ||
| + | |||
| + | Для экономии памяти фиктивные листья можно сделать одним общим фиктивным листом. | ||
== Свойства == | == Свойства == | ||
| − | # | + | ===Оригинальные=== |
| − | # | + | Красно-чёрным называется бинарное поисковое дерево, у которого каждому узлу сопоставлен дополнительный атрибут {{---}} цвет и для которого выполняются следующие свойства: |
| − | # | + | # Каждый узел промаркирован красным или чёрным цветом |
| − | # | + | # Корень и конечные узлы (листья) дерева {{---}} чёрные |
| + | # У красного узла родительский узел {{---}} чёрный | ||
| + | # Все простые пути из любого узла x до листьев содержат одинаковое количество чёрных узлов | ||
| + | # Чёрный узел может иметь чёрного родителя | ||
| + | [[Файл:konspv2.jpg|350px|thumb|Ослабленное красно-чёрное дерево.]] | ||
| + | |||
| + | Определим ослабленное красно-чёрное дерево как красно-чёрное дерево, корень которого может быть как чёрным, так и красным. Докажем, что при таком условии не будут выполняться и некоторые другие свойства красно-черных деревьев. При добавлении вершины около корня могут возникнуть повороты, и корневая вершина перейдет в какое-то поддерево. Из-за этого может возникнуть ситуация, в которой подряд будут идти две красные вершины. То же самое может произойти из-за перекрашиваний возле корня. Если мы продолжим вставлять элементы подобным образом, свойства дерева перестанут выполняться, и оно перестанет быть сбалансированным. Таким образом, время выполнения некоторых операций ухудшится. | ||
| + | |||
| + | Перед тем, как перейдем к примеру, договоримся, что мы разрешим в ослабленном красно-чёрном дереве при первом добавлении вершин (обеих, правой и левой) к красному корню делать их черными (немного модифицированный алгоритм вставки). Предыдущее условие можно заменить на другое, позволяющее корню иметь красных детей. | ||
| + | |||
| + | Рассмотрим пример справа. Получим такое дерево добавляя ключи в следующем порядке: $10$, $6$, $45$, $4$, $8$. На примере можно видеть, что после добавления вершины с ключом <tex>0</tex> и соответствующих перекрашиваний вершина с ключом <tex>6</tex> становится красной с красным родителем. Дальше добавим <tex>5</tex>. Так как мы добавляем к черной вершине, все свойства дерева сохраняются без перекрашиваний. Но добавим после этого <tex>(-3)</tex>. Тогда вершина с ключом <tex>4</tex> станет красной (<tex>0</tex> и <tex>5</tex> {{---}} черными) и у нас образуются три красные вершины подряд. Продолжая добавлять вершины таким образом, мы можем сделать сильно разбалансированное дерево. | ||
| + | |||
| + | ===Альтернативные=== | ||
| + | В книге Кормена "Алгоритмы: построение и анализ" дается немного иное определение красно-черного дерева, а именно: | ||
| + | |||
| + | Двоичное дерево поиска является красно-чёрным, если обладает следующими свойствами: | ||
| + | # Каждая вершина {{---}} либо красная, либо черная | ||
| + | # Каждый лист {{---}} черный | ||
| + | # Если вершина красная, оба ее ребенка черные | ||
| + | # Все пути, идущие от корня к листьям, содержат одинаковое количество черных вершин | ||
| + | |||
| + | То, что только черная вершина может иметь красных детей, совместно с <tex>4</tex>-ым свойством говорит о том, что корень дерева должен быть черным, а значит определения можно считать эквивалентными. | ||
== Высота красно-черного дерева == | == Высота красно-черного дерева == | ||
| − | + | {{Определение | |
| + | |definition=Будем называть '''чёрной высотой''' (англ. ''black-height'') вершины <tex>x</tex> число чёрных вершин на пути из <tex>x</tex> в лист. | ||
| + | }} | ||
| + | |||
| + | {{Лемма | ||
| + | |statement= В красно-черном дереве с черной высотой <tex>hb</tex> количество внутренних вершин не менее <tex>2^{hb-1}-1</tex>. | ||
| + | |proof= | ||
| + | Докажем по индукции по обычной высоте $h(x)$, что поддерево любого узла <tex>x</tex> с черной высотой <tex>hb(x)</tex> содержит не менее <tex>2^{hb(x)-1} - 1</tex> внутренних узлов. | ||
| + | Здесь $h(x)$ {{---}} кратчайшее расстояние от вершины $x$ до какого-то из листьев. | ||
| + | |||
| + | '''База индукции:''' | ||
| + | |||
| + | Если высота узла <tex>x</tex> равна <tex>1</tex>, то <tex>x</tex> {{---}} это лист, <tex>hb(x) = 1</tex>, <tex>2^{1-1} - 1 = 0</tex>. | ||
| − | ''' | + | '''Переход:''' |
| − | + | Так как любая внутренняя вершина (вершина, у которой высота положительна) имеет двух потомков, то применим предположение индукции к ним {{---}} их высоты на единицу меньше высоты $x$. | |
| − | + | Тогда черные высоты детей могут быть $hb(x)$ или $hb(x)-1$ {{---}} если потомок красный или черный соответственно. | |
| − | <tex>N >= 2^{h/2}-1</tex> | + | Тогда по предположению индукции в каждом из поддеревьев не менее $2^{hb(x)-2}-1$ вершин. Тогда всего в поддереве не менее $2\cdot(2^{hb(x)-2}-1)+1 = 2^{hb(x)-1}-1$ вершин ($+1$ {{---}} мы учли еще саму вершину $x$). |
| + | |||
| + | Переход доказан. | ||
| + | Теперь, если мы рассмотрим корень всего дерева в качестве $x$, то получится, что всего вершин в дереве не менее $2^{hb-1}-1$. | ||
| + | |||
| + | Следовательно, утверждение верно и для всего дерева. | ||
| + | }} | ||
| + | |||
| + | {{Теорема | ||
| + | |statement=Красно-чёрное дерево с <tex>N</tex> ключами имеет высоту <tex>h = O(\log N)</tex>. | ||
| + | |proof= | ||
| + | Рассмотрим красно-чёрное дерево с высотой <tex>h</tex>. Так как у красной вершины чёрные дети (по свойству $3$) количество красных вершин не больше $\dfrac{h}{2}$. | ||
| + | Тогда чёрных вершин не меньше, чем <tex>\dfrac{h}{2} - 1</tex>. | ||
| + | |||
| + | По доказанной лемме, для количества внутренних вершин в дереве <tex>N</tex> выполняется неравенство: | ||
| + | |||
| + | <tex>N \geqslant 2^{h/2}-1</tex> | ||
Прологарифмировав неравенство, имеем: | Прологарифмировав неравенство, имеем: | ||
| − | <tex>\log(N+1) | + | <tex>\log(N+1) \geqslant \dfrac{h}{2}</tex> |
| − | |||
| − | |||
| − | <tex> | + | <tex>2\log(N+1) \geqslant h</tex> |
| − | + | <tex>h \leqslant 2\log(N+1)</tex> | |
| − | + | }} | |
== Операции == | == Операции == | ||
| + | Узел, с которым мы работаем, на картинках имеет имя <tex>x</tex>. | ||
=== Вставка элемента === | === Вставка элемента === | ||
| − | Каждый элемент вставляется вместо листа, поэтому для выбора места вставки идём от корня до тех пор, пока указатель на следующего сына не станет nil( | + | Каждый элемент вставляется вместо листа, поэтому для выбора места вставки идём от корня до тех пор, пока указатель на следующего сына не станет <tex>nil</tex> (то есть этот сын {{---}} лист). Вставляем вместо него новый элемент с нулевыми потомками и красным цветом. Теперь проверяем балансировку. Если отец нового элемента черный, то никакое из свойств дерева не нарушено. Если же он красный, то нарушается свойство <tex>3</tex>, для исправления достаточно рассмотреть два случая: |
| + | # "Дядя" этого узла тоже красный. Тогда, чтобы сохранить свойства <tex>3</tex> и <tex>4</tex>, просто перекрашиваем "отца" и "дядю" в чёрный цвет, а "деда" {{---}} в красный. В таком случае черная высота в этом поддереве одинакова для всех листьев и у всех красных вершин "отцы" черные. Проверяем, не нарушена ли балансировка. Если в результате этих перекрашиваний мы дойдём до корня, то в нём в любом случае ставим чёрный цвет, чтобы дерево удовлетворяло свойству <tex>2</tex>. [[Файл:Untitled-1.png|200px]] | ||
| + | # "Дядя" чёрный. Если выполнить только перекрашивание, то может нарушиться постоянство чёрной высоты дерева по всем ветвям. Поэтому выполняем поворот. Если добавляемый узел был правым потомком, то необходимо сначала выполнить левое вращение, которое сделает его левым потомком. Таким образом, свойство <tex>3</tex> и постоянство черной высоты сохраняются. | ||
| − | + | [[Файл:Untitled-2.png|250px|]] | |
| − | + | '''Псевдокод:''' | |
| + | '''func''' insert(key) | ||
| + | Node t = Node(key, red, ''nil'', ''nil'') <font color=green>// конструктор, в который передаем ключ, цвет, левого и правого ребенка </font> | ||
| + | '''if''' дерево пустое | ||
| + | root = t | ||
| + | t.parent = ''nil'' | ||
| + | '''else''' | ||
| + | Node p = root | ||
| + | Node q = ''nil'' | ||
| + | '''while''' p != ''nil'' <font color=green>// спускаемся вниз, пока не дойдем до подходящего листа </font> | ||
| + | q = p | ||
| + | '''if''' p.key < t.key | ||
| + | p = p.right | ||
| + | '''else''' | ||
| + | p = p.left | ||
| + | t.parent = q | ||
| + | <font color=green>// добавляем новый элемент красного цвета </font> | ||
| + | '''if''' q.key < t.key | ||
| + | q.right = t | ||
| + | '''else''' | ||
| + | q.left = t | ||
| + | fixInsertion(t) <font color=green>// проверяем, не нарушены ли свойства красно-черного дерева </font> | ||
| − | + | '''func''' fixInsertion(t: '''Node''') | |
| − | + | '''if''' t {{---}} корень | |
| − | + | t = black | |
| + | '''return''' | ||
| + | <font color=green>// далее все предки упоминаются относительно t </font> | ||
| + | '''while''' "отец" красный <font color=green>// нарушается свойство <tex>3</tex> </font> | ||
| + | '''if''' "отец" {{---}} левый ребенок | ||
| + | '''if''' есть красный "дядя" | ||
| + | parent = black | ||
| + | uncle = black | ||
| + | grandfather = red | ||
| + | t = grandfather | ||
| + | '''else''' | ||
| + | '''if''' t {{---}} правый сын | ||
| + | t = parent | ||
| + | leftRotate(t) | ||
| + | parent = black | ||
| + | grandfather = red | ||
| + | rightRotate(grandfather) | ||
| + | '''else''' <font color=green>// "отец" {{---}} правый ребенок </font> | ||
| + | '''if''' есть красный "дядя" | ||
| + | parent = black | ||
| + | uncle = black | ||
| + | grandfather = red | ||
| + | t = grandfather | ||
| + | '''else''' <font color=green>// нет "дяди" </font> | ||
| + | '''if''' t {{---}} левый ребенок | ||
| + | t = t.parent | ||
| + | rightRotate(t) | ||
| + | parent = black | ||
| + | grandfather = red | ||
| + | leftRotate(grandfather) | ||
| + | root = black <font color=green>// восстанавливаем свойство корня </font> | ||
=== Удаление вершины === | === Удаление вершины === | ||
При удалении вершины могут возникнуть три случая в зависимости от количества её детей: | При удалении вершины могут возникнуть три случая в зависимости от количества её детей: | ||
| − | + | * Если у вершины нет детей, то изменяем указатель на неё у родителя на <tex>nil</tex>. | |
| − | + | * Если у неё только один ребёнок, то делаем у родителя ссылку на него вместо этой вершины. | |
| − | + | * Если же имеются оба ребёнка, то находим вершину со следующим значением ключа. У такой вершины нет левого ребёнка (так как такая вершина находится в правом поддереве исходной вершины и она самая левая в нем, иначе бы мы взяли ее левого ребенка. Иными словами сначала мы переходим в правое поддерево, а после спускаемся вниз в левое до тех пор, пока у вершины есть левый ребенок). Удаляем уже эту вершину описанным во втором пункте способом, скопировав её ключ в изначальную вершину. | |
| − | Проверим балансировку дерева. | + | Проверим балансировку дерева. Так как при удалении красной вершины свойства дерева не нарушаются, то восстановление балансировки потребуется только при удалении чёрной. Рассмотрим ребёнка удалённой вершины. |
| − | + | * Если брат этого ребёнка красный, то делаем вращение вокруг ребра между отцом и братом, тогда брат становится родителем отца. Красим его в чёрный, а отца {{---}} в красный цвет, сохраняя таким образом черную высоту дерева. Хотя все пути по-прежнему содержат одинаковое количество чёрных узлов, сейчас <tex>x</tex> имеет чёрного брата и красного отца. Таким образом, мы можем перейти к следующему шагу. | |
| + | *: | ||
| + | *:[[Файл:Untitled-3.png|400px|]] | ||
| + | *: | ||
| + | * Если брат текущей вершины был чёрным, то получаем три случая: | ||
| + | ** Оба ребёнка у брата чёрные. Красим брата в красный цвет и рассматриваем далее отца вершины. Делаем его черным, это не повлияет на количество чёрных узлов на путях, проходящих через <tex>b</tex>, но добавит один к числу чёрных узлов на путях, проходящих через <tex>x</tex>, восстанавливая тем самым влиянние удаленного чёрного узла. Таким образом, после удаления вершины черная глубина от отца этой вершины до всех листьев в этом поддереве будет одинаковой. | ||
| + | **: | ||
| + | **:[[Файл:Untitled-4.png|400px|]] | ||
| + | **: | ||
| + | ** Если у брата правый ребёнок чёрный, а левый красный, то перекрашиваем брата и его левого сына и делаем вращение. Все пути по-прежнему содержат одинаковое количество чёрных узлов, но теперь у <tex>x</tex> есть чёрный брат с красным правым потомком, и мы переходим к следующему случаю. Ни <tex>x</tex>, ни его отец не влияют на эту трансформацию. | ||
| + | **: | ||
| + | **:[[Файл:Untitled-5.png|400px|]] | ||
| + | **: | ||
| + | ** Если у брата правый ребёнок красный, то перекрашиваем брата в цвет отца, его ребёнка и отца {{---}} в чёрный, делаем вращение. Поддерево по-прежнему имеет тот же цвет корня, поэтому свойство <tex>3</tex> и <tex>4</tex> не нарушаются. Но у <tex>x</tex> теперь появился дополнительный чёрный предок: либо <tex>a</tex> стал чёрным, или он и был чёрным и <tex>b</tex> был добавлен в качестве чёрного дедушки. Таким образом, проходящие через <tex>x</tex> пути проходят через один дополнительный чёрный узел. Выходим из алгоритма. | ||
| + | **: | ||
| + | **: [[Файл:Untitled-6.png|400px|]] | ||
| − | + | Продолжаем тот же алгоритм, пока текущая вершина чёрная и мы не дошли до корня дерева. | |
| + | Из рассмотренных случаев ясно, что при удалении выполняется не более трёх вращений. | ||
| − | + | '''Псевдокод:''' | |
| − | + | '''func''' delete(key) | |
| + | Node p = root | ||
| + | <font color=green>// находим узел с ключом key</font> | ||
| + | '''while''' p.key != key | ||
| + | '''if''' p.key < key | ||
| + | p = p.right | ||
| + | '''else''' | ||
| + | p = p.left | ||
| + | '''if''' у p нет детей | ||
| + | '''if''' p {{---}} корень | ||
| + | root = ''nil'' | ||
| + | '''else''' | ||
| + | ссылку на p у "отца" меняем на ''nil'' | ||
| + | '''return''' | ||
| + | Node y = ''nil'' | ||
| + | Node q = ''nil'' | ||
| + | '''if''' один ребенок | ||
| + | ссылку на у от "отца" меняем на ребенка y | ||
| + | '''else''' | ||
| + | <font color=green>// два ребенка</font> | ||
| + | y = вершина, со следующим значением ключа <font color=green>// у нее нет левого ребенка </font> | ||
| + | '''if''' y имеет правого ребенка | ||
| + | y.right.parent = y.parent | ||
| + | '''if''' y {{---}} корень | ||
| + | root = y.right | ||
| + | '''else''' | ||
| + | у родителя ссылку на y меняем на ссылку на первого ребенка y | ||
| + | '''if''' y != p | ||
| + | p.colour = y.colour | ||
| + | p.key = y.key | ||
| + | '''if''' y.colour == black | ||
| + | <font color=green>// при удалении черной вершины могла быть нарушена балансировка</font> | ||
| + | fixDeleting(q) | ||
| + | |||
| − | + | '''func''' fixDeleting(p: '''Node''') | |
| + | <font color=green>// далее родственные связи относительно p</font> | ||
| + | '''while''' p {{---}} черный узел и не корень | ||
| + | '''if''' p {{---}} левый ребенок | ||
| + | '''if''' "брат" красный | ||
| + | brother = black | ||
| + | parent = red | ||
| + | leftRotate(parent) | ||
| + | '''if''' у "брата" черные дети <font color=green>// случай <tex>1:</tex> "брат" красный с черными детьми</font> | ||
| + | brother = red | ||
| + | '''else''' | ||
| + | '''if''' правый ребенок "брата" черный <font color=green>// случай, рассматриваемый во втором подпункте:</font> | ||
| + | brother.left = black <font color=green>// "брат" красный с черными правым ребенком</font> | ||
| + | brother = red | ||
| + | rightRotate(brother) | ||
| + | brother.colour = parent.colour <font color=green>// случай, рассматриваемый в последнем подпункте</font> | ||
| + | parent = black | ||
| + | brother.right = black | ||
| + | leftRotate(parent) | ||
| + | p = root | ||
| + | '''else''' <font color=green>// p {{---}} правый ребенок</font> | ||
| + | <font color=green>// все случаи аналогичны тому, что рассмотрено выше</font> | ||
| + | '''if''' "брат" красный | ||
| + | brother = black | ||
| + | parent = red | ||
| + | rightRotate(p.parent) | ||
| + | '''if''' у "брата" черные дети | ||
| + | brother = red | ||
| + | '''else''' | ||
| + | '''if''' левый ребенок "брата" черный | ||
| + | brother.right = black | ||
| + | brother = red | ||
| + | leftRotate(brother); | ||
| + | brother = parent | ||
| + | parent = black | ||
| + | brother.left = black | ||
| + | rightRotate(p.parent) | ||
| + | p = root | ||
| + | p = black | ||
| + | root = black | ||
| − | + | === Объединение красно-чёрных деревьев === | |
| + | Объединение двух красно-чёрных деревьев <tex>T_{1}</tex> и <tex>T_{2}</tex> по ключу <tex>k</tex> возвращает дерево с элементами из $T_2$, $T_1$ и $k$. Требование: ключ $k$ {{---}} разделяющий. То есть $\forall k_1\in T_1, k_2 \in T_2: k_1\leqslant k\leqslant k_2$. | ||
| − | + | Если оба дерева имеют одинаковую черную высоту, то результатом будет дерево с черным корнем $k$, левым и правым поддеревьями $k_1$ и $k_2$ соответствено. | |
| − | + | Теперь пусть у $T_1$ черная высота больше (иначе аналогично). | |
| − | + | * Находим в дереве $T_1$ вершину $y$ на черной высоте, как у дерева $T_2$ вершину с максимальным ключом. Это делается несложно (особенно если мы знаем черную высоту дерева): спускаемся вниз, поддерживая текущую черную высоту. | |
| + | *:Идем вправо. Когда высота станет равной высоте $T_2$, остановимся. | ||
| + | *:Заметим, что черная высота $T_2\geqslant 2$. Поэтому в дереве $T_1$ мы не будем ниже, чем $2$. Пусть мы не можем повернуть направо (сын нулевой), тогда наша высота $2$ (если мы в черной вершине) или $1$ (если в красной). Второго случая быть не может, ибо высота $T_2\geqslant 2$, а в первом случае мы должны были завершить алгоритм, когда пришли в эту вершину. | ||
| + | *:Очевидно, мы окажемся в черной вершине (ибо следующий шаг даст высоту меньше). Очевидно, мы оказались на нужной высоте. | ||
| + | *:Теперь пусть мы попали не туда. То есть существует путь от корня до другой вершины. Посмотрим на то место, где мы не туда пошли. Если мы пошли вправо, а надо бы влево, то $x$ имеет больший ключ (по свойству дерева поиска). А если пошли влево, а не вправо, значит правого сына и нет (точнее, есть, но он нулевой), значит в правом поддереве вообще нет вершин. | ||
| + | *:Более того, все вершины с высотами меньше $y$, которые имеют ключ больше $y$, будут находиться в поддереве $y$. Действительно, мы всегда идем вправо. Инвариант алгоритма на каждом шаге {{---}} в поддереве текущей вершины содержатся все вершины, ключ которых больше текущего. Проверяется очевидно. | ||
| + | *:Еще поймем, как будем хранить черную высоту дерева. Изначально она нулевая (в пустом дереве). Далее просто поддерживаем ее при операциях вставки и удаления. | ||
| + | * Объединим поддерево. $k$ будет корнем, левым и правым сыновьями будут $T_y$ и $T_2$ соответственно. | ||
| + | *:Покажем, что свойства дерева поиска не нарушены. | ||
| + | *:Так как все ключи поддерева $y$ не более $k$ и все ключи $T_2$ не менее $k$, то в новом поддереве с корнем $k$ свойства выполняются. | ||
| + | *:Так как $k$ больше любого ключа из $T_1$, то выполняется и для всего дерева. | ||
| + | * Красим $k$ в красный цвет. Тогда свойство $4$ будет выполнено. Далее поднимаемся вверх, как во вставке операциях, поворотами исправляя нарушение правила $3$. | ||
| + | * В конце корень красим в черный, если до этого был красный (это всегда можно сделать, ничего не нарушив). | ||
| − | + | '''Псевдокод:''' | |
| + | '''func''' join(T_1, T_2, k) | ||
| + | '''if''' черные высоты равны | ||
| + | return Node(k, black, T_1, T_2) | ||
| + | '''if''' высота T_1 больше | ||
| + | T' = joinToRight(T_1, T_2, k) | ||
| + | T'.color = black | ||
| + | return T' | ||
| + | '''else''' | ||
| + | T' = joinToLeft(T_1, T_2, k) | ||
| + | T'.color = black | ||
| + | return T' | ||
| + | |||
| + | '''func''' joinToRight(T_1, T_2, k) | ||
| + | Y = find(T_1, bh(T_2)) | ||
| + | T' = Node(k, red, Y, T_2) | ||
| + | '''while''' нарушение | ||
| + | действуем как во вставке | ||
| + | return T' | ||
| + | |||
| + | '''func''' find(T, h) | ||
| + | curBH = bh(T) | ||
| + | curV = T | ||
| + | '''while''' curBH != h | ||
| + | curV = curV.right | ||
| + | '''if''' curV.color == black | ||
| + | --curBH | ||
| + | return curV | ||
| − | === | + | Сложность: $\mathcal{O}(T_1.h-T_2.h)=\mathcal{O}(\log(n))$ |
| − | + | ||
| − | + | === Разрезание красно-чёрного дерева === | |
| − | + | Разрезание дерева по ключу $k$ вернет два дерева, ключи первого меньше $k$, а второго {{---}} не меньше. | |
| + | |||
| + | Пройдем вниз как во время поиска. Все левые поддеревья вершин пути, корень которых не в пути, будут в первом поддереве. Аналогично правые {{---}} в правом. | ||
| + | Теперь поднимаемся и последовательно сливаем деревья справа и слева с ответами. | ||
| + | |||
| + | За счет того, что функция '''$join$''' работает за разницу высот, и мы объединяем снизу, то, благодаря телескопическому эффекту на работу времени будут влиять только крайние слагаемые, которые порядка глубины дерева. | ||
| + | |||
| + | '''Псевдокод''' | ||
| + | '''func''' split(T, k) | ||
| + | '''if''' T = nil | ||
| + | return $\langle$nil, nil$\rangle$ | ||
| + | '''if''' k < T.key | ||
| + | $\langle$L',R'$\rangle$ = split(L,k) | ||
| + | return $\langle$L',join(R',T.key,R)$\rangle$ | ||
| + | '''else''' | ||
| + | $\langle$L',R'$\rangle$ = split(R,k) | ||
| + | return $\langle$join(L,T.key,L'),R)$\rangle$ | ||
| + | |||
| + | Сложность: $\mathcal{O}(\log(n))$ | ||
| + | |||
| + | Точно такой же алгоритм в разрезании AVL деревьев. Оно и понятно {{---}} нам нужна лишь корректная функция '''$join$''', работающая за разницу высот. | ||
| + | |||
| + | == Преимущества красно-чёрных деревьев == | ||
| + | #Самое главное преимущество красно-черных деревьев в том, что при вставке выполняется не более <tex>O(1)</tex> вращений. Это важно, например, в алгоритме построения [[Динамическая выпуклая оболочка (достаточно log^2 на добавление/удаление)|динамической выпуклой оболочки]]. Ещё важно, что примерно половина вставок и удалений произойдут задаром. | ||
| + | #Процедуру балансировки практически всегда можно выполнять параллельно с процедурами поиска, так как алгоритм поиска не зависит от атрибута цвета узлов. | ||
| + | #Сбалансированность этих деревьев хуже, чем у [[АВЛ-дерево | АВЛ]], но работа по поддержанию сбалансированности в красно-чёрных деревьях обычно эффективнее. Для балансировки красно-чёрного дерева производится минимальная работа по сравнению с АВЛ-деревьями. | ||
| + | #Использует всего $1$ бит дополнительной памяти для хранения цвета вершины. Но на самом деле в современных вычислительных системах память выделяется кратно байтам, поэтому это не является преимуществом относительно, например, АВЛ-дерева, которое хранит $2$ бита. Однако есть реализации красно-чёрного дерева, которые хранят значение цвета в бите. Пример {{---}} Boost Multiindex. В этой реализации уменьшается потребление памяти красно-чёрным деревом, так как бит цвета хранится не в отдельной переменной, а в одном из указателей узла дерева. | ||
| + | |||
| + | Красно-чёрные деревья являются наиболее активно используемыми на практике самобалансирующимися деревьями поиска. В частности, ассоциативные контейнеры библиотеки STL(map, set, multiset, multimap) основаны на красно-чёрных деревьях. TreeMap в Java тоже реализован на основе красно-чёрных деревьев. | ||
| + | |||
| + | == Связь с [[2-3_дерево | 2-3 и 2-4 деревьями]] == | ||
| + | |||
| + | === Изоморфизм деревьев === | ||
| + | |||
| + | Красно-черные деревья изоморфны [[B-дерево | B-деревьям]] $4$ порядка. Реализация B-деревьев трудна на практике, поэтому для них был придуман аналог, называемый симметричным бинарным B-деревом<ref>[http://rflinux.blogspot.ru/2011/10/red-black-trees.html Абстрактные типы данных {{---}} Красно-чёрные деревья (Red black trees)]</ref>. Особенностью симметричных бинарных B-деревьев является наличие горизонтальных и вертикальных связей. Вертикальные связи отделяют друг от друга разные узлы, а горизонтальные соединяют элементы, хранящиеся в одном узле B-дерева. Для различения вертикальных и горизонтальных связей вводится новый атрибут узла {{---}} цвет. Только один из элементов узла в B-дереве красится в черный цвет. Горизонтальные связи ведут из черного узла в красный узел, а вертикальные могут вести из любого узла в черный. | ||
| + | |||
| + | [[Файл:Rbtree.png|750px|]] | ||
| + | |||
| + | === Корректность сопоставления деревьев === | ||
| + | |||
| + | Сопоставив таким образом цвета узлам дерева, можно проверить, что полученное дерево удовлетворяет всем свойствам красно-черного дерева. | ||
| + | {{Утверждение | ||
| + | |statement= | ||
| + | У красного узла родитель не может быть красного цвета. | ||
| + | |proof= | ||
| + | В узле 2-4 дерева содержится не более трех элементов, один из которых обязательно красится в черный при переходе к симметричному бинарному B-дереву. Тогда оставшиеся красные элементы, если они есть, подвешиваются к черному. Из этих элементов могут идти ребра в следующий узел 2-4 дерева. В этом узле обязательно есть черная вершина, в нее и направляется ребро. Оставшиеся элементы узла, если они есть, подвешиваются к черной вершине аналогично первому узлу. Таким образом, ребро из красной вершины никогда не попадает в красную, значит у красного элемента родитель не может быть красным. | ||
| + | }} | ||
| + | {{Утверждение | ||
| + | |statement= | ||
| + | Число черных узлов на любом пути от листа до вершины одинаково. | ||
| + | |proof= | ||
| + | В B-дереве глубина всех листьев одинакова, следовательно, одинаково и количество внутренних узлов на каждом пути. Мы сопоставляем чёрный цвет одному элементу внутреннего узла B-дерева. Значит, количество чёрных элементов на любом пути от листа до вершины одинаково. | ||
| + | }} | ||
| + | {{Утверждение | ||
| + | |statement= | ||
| + | Корень дерева {{---}} черный. | ||
| + | |proof= | ||
| + | Если в корне один элемент, то он {{---}} чёрный. Если же в корне несколько элементов, то заметим, что один элемент окрашен в чёрный цвет, остальные {{---}} в красный. Горизонтальные связи, соединяющие элементы внутри одного узнала, ведут из чёрного элемента в красный, следовательно, красные элементы будут подвешены к чёрному. Он и выбирается в качестве корня симметричного бинарного B-дерева. | ||
| + | }} | ||
| + | |||
| + | === Сопоставление операций в деревьях === | ||
| + | |||
| + | Все операции, совершаемые в B-дереве, сопоставляются операциям в красно-черном дереве. Для этого достаточно доказать, что изменение узла в B-дереве соответствует повороту в красно-черном дереве. | ||
| + | {{Утверждение | ||
| + | |statement= | ||
| + | Изменение узла в B-дереве соответствует повороту в красно-черном дереве. | ||
| + | |proof= | ||
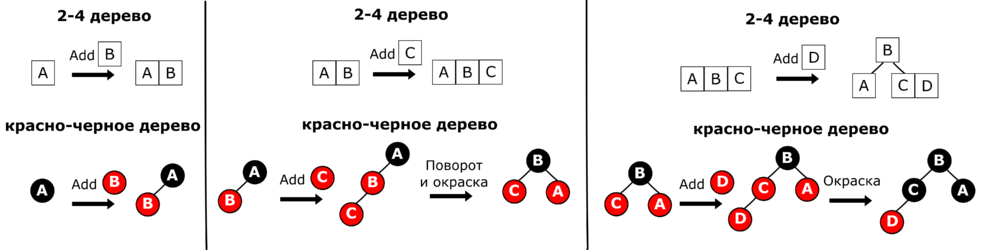
| + | В 2-4 дереве изменение узла необходимо при добавлении к нему элемента. Рассмотрим, как будет меняться структура B-дерева и, соответственно, красно-черного дерева при добавлении элемента: | ||
| + | |||
| + | * Если в узле содержался один элемент, то происходит добавление второго элемента, соответствующее добавлению красного элемента в красно-черное дерево. | ||
| + | |||
| + | * Если в узле содержалось два элемента, то происходит добавление третьего элемента, что соответствует повороту и перекрашиванию вершин в красно-черном дереве. | ||
| + | |||
| + | * Если в узле содержалось три элемента, то один из элементов узла становится самостоятельным узлом, к которому подвешиваются узел из пары элементов и узел из одного элемента. Эта операция соответствует перекрашиванию яруса красно-черного дерева из красного в черный цвет. | ||
| + | |||
| + | [[Файл:Rbtree2.png|1000px|]] | ||
| + | |||
| + | При удалении элемента из узла B-дерева совершаются аналогичные процессы поворота и окраски вершин в красно-черном дереве, только в обратном направлении. Так как все операции в 2-4 дереве происходят за счет изменения узлов, то они эквивалентны соответствующим операциям в красно-черном дереве. | ||
| + | }} | ||
| + | |||
| + | {{Теорема | ||
| + | |statement= | ||
| + | Приведенное выше сопоставление B-деревьев и красно-черных деревьев является изоморфизмом. | ||
| + | |proof= | ||
| + | Доказательство следует непосредственно из приведенных выше утверждений. | ||
| + | }} | ||
| + | |||
| + | ==См. также== | ||
| + | |||
| + | * [[Дерево поиска, наивная реализация|Дерево поиска, наивная реализация]] | ||
| + | * [[АВЛ-дерево|АВЛ-дерево]] | ||
| + | * [[2-3 дерево|2-3 дерево]] | ||
| + | |||
| + | == Примечания == | ||
| + | <references/> | ||
| + | |||
| + | ==Источники информации== | ||
| − | + | * [http://ru.wikipedia.org/wiki/%CA%F0%E0%F1%ED%EE-%F7%B8%F0%ED%EE%E5_%E4%E5%F0%E5%E2%EE Википедия {{---}} Красно-чёрное дерево] | |
| + | * [http://algolist.manual.ru/ds/rbtree.php AlgoList {{---}} Красно-черные деревья] | ||
| + | * [http://lectures.stargeo.ru/alg/algorithms.htm#_Toc241931998 Lectures.stargeo {{---}} Конспект лекций] | ||
| + | * [http://nord.org.ua/static/course/algo_2009/lecture10.pdf Курс kiev-clrs {{---}} Лекция 10. Красно-чёрные деревья] | ||
| + | * [http://rain.ifmo.ru/cat/view.php/vis/trees/red-black-2002 Визуализатор] | ||
| + | * [http://rflinux.blogspot.ru/2011/10/red-black-trees.html Абстрактные типы данных {{---}} Красно-чёрные деревья (Red black trees)] | ||
| − | |||
| − | + | [[Категория:Дискретная математика и алгоритмы]] | |
| − | + | [[Категория:Деревья поиска]] | |
| − | |||
| − | |||
Текущая версия на 19:17, 4 сентября 2022
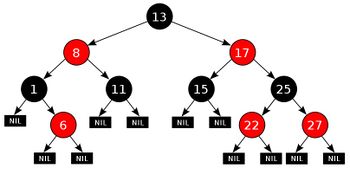
Красно-чёрное дерево (англ. red-black tree) — двоичное дерево поиска, в котором баланс осуществляется на основе "цвета" узла дерева, который принимает только два значения: "красный" (англ. red) и "чёрный" (англ. black).
При этом все листья дерева являются фиктивными и не содержат данных, но относятся к дереву и являются чёрными.
Для экономии памяти фиктивные листья можно сделать одним общим фиктивным листом.
Свойства
Оригинальные
Красно-чёрным называется бинарное поисковое дерево, у которого каждому узлу сопоставлен дополнительный атрибут — цвет и для которого выполняются следующие свойства:
- Каждый узел промаркирован красным или чёрным цветом
- Корень и конечные узлы (листья) дерева — чёрные
- У красного узла родительский узел — чёрный
- Все простые пути из любого узла x до листьев содержат одинаковое количество чёрных узлов
- Чёрный узел может иметь чёрного родителя
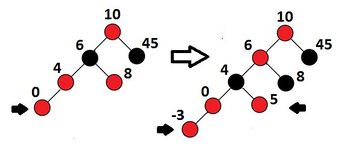
Определим ослабленное красно-чёрное дерево как красно-чёрное дерево, корень которого может быть как чёрным, так и красным. Докажем, что при таком условии не будут выполняться и некоторые другие свойства красно-черных деревьев. При добавлении вершины около корня могут возникнуть повороты, и корневая вершина перейдет в какое-то поддерево. Из-за этого может возникнуть ситуация, в которой подряд будут идти две красные вершины. То же самое может произойти из-за перекрашиваний возле корня. Если мы продолжим вставлять элементы подобным образом, свойства дерева перестанут выполняться, и оно перестанет быть сбалансированным. Таким образом, время выполнения некоторых операций ухудшится.
Перед тем, как перейдем к примеру, договоримся, что мы разрешим в ослабленном красно-чёрном дереве при первом добавлении вершин (обеих, правой и левой) к красному корню делать их черными (немного модифицированный алгоритм вставки). Предыдущее условие можно заменить на другое, позволяющее корню иметь красных детей.
Рассмотрим пример справа. Получим такое дерево добавляя ключи в следующем порядке: $10$, $6$, $45$, $4$, $8$. На примере можно видеть, что после добавления вершины с ключом и соответствующих перекрашиваний вершина с ключом становится красной с красным родителем. Дальше добавим . Так как мы добавляем к черной вершине, все свойства дерева сохраняются без перекрашиваний. Но добавим после этого . Тогда вершина с ключом станет красной ( и — черными) и у нас образуются три красные вершины подряд. Продолжая добавлять вершины таким образом, мы можем сделать сильно разбалансированное дерево.
Альтернативные
В книге Кормена "Алгоритмы: построение и анализ" дается немного иное определение красно-черного дерева, а именно:
Двоичное дерево поиска является красно-чёрным, если обладает следующими свойствами:
- Каждая вершина — либо красная, либо черная
- Каждый лист — черный
- Если вершина красная, оба ее ребенка черные
- Все пути, идущие от корня к листьям, содержат одинаковое количество черных вершин
То, что только черная вершина может иметь красных детей, совместно с -ым свойством говорит о том, что корень дерева должен быть черным, а значит определения можно считать эквивалентными.
Высота красно-черного дерева
| Определение: |
| Будем называть чёрной высотой (англ. black-height) вершины число чёрных вершин на пути из в лист. |
| Лемма: |
В красно-черном дереве с черной высотой количество внутренних вершин не менее . |
| Доказательство: |
|
Докажем по индукции по обычной высоте $h(x)$, что поддерево любого узла с черной высотой содержит не менее внутренних узлов. Здесь $h(x)$ — кратчайшее расстояние от вершины $x$ до какого-то из листьев. База индукции: Если высота узла равна , то — это лист, , . Переход: Так как любая внутренняя вершина (вершина, у которой высота положительна) имеет двух потомков, то применим предположение индукции к ним — их высоты на единицу меньше высоты $x$. Тогда черные высоты детей могут быть $hb(x)$ или $hb(x)-1$ — если потомок красный или черный соответственно. Тогда по предположению индукции в каждом из поддеревьев не менее $2^{hb(x)-2}-1$ вершин. Тогда всего в поддереве не менее $2\cdot(2^{hb(x)-2}-1)+1 = 2^{hb(x)-1}-1$ вершин ($+1$ — мы учли еще саму вершину $x$). Переход доказан. Теперь, если мы рассмотрим корень всего дерева в качестве $x$, то получится, что всего вершин в дереве не менее $2^{hb-1}-1$. Следовательно, утверждение верно и для всего дерева. |
| Теорема: |
Красно-чёрное дерево с ключами имеет высоту . |
| Доказательство: |
|
Рассмотрим красно-чёрное дерево с высотой . Так как у красной вершины чёрные дети (по свойству $3$) количество красных вершин не больше $\dfrac{h}{2}$. Тогда чёрных вершин не меньше, чем . По доказанной лемме, для количества внутренних вершин в дереве выполняется неравенство:
Прологарифмировав неравенство, имеем:
|
Операции
Узел, с которым мы работаем, на картинках имеет имя .
Вставка элемента
Каждый элемент вставляется вместо листа, поэтому для выбора места вставки идём от корня до тех пор, пока указатель на следующего сына не станет (то есть этот сын — лист). Вставляем вместо него новый элемент с нулевыми потомками и красным цветом. Теперь проверяем балансировку. Если отец нового элемента черный, то никакое из свойств дерева не нарушено. Если же он красный, то нарушается свойство , для исправления достаточно рассмотреть два случая:
- "Дядя" этого узла тоже красный. Тогда, чтобы сохранить свойства и , просто перекрашиваем "отца" и "дядю" в чёрный цвет, а "деда" — в красный. В таком случае черная высота в этом поддереве одинакова для всех листьев и у всех красных вершин "отцы" черные. Проверяем, не нарушена ли балансировка. Если в результате этих перекрашиваний мы дойдём до корня, то в нём в любом случае ставим чёрный цвет, чтобы дерево удовлетворяло свойству .
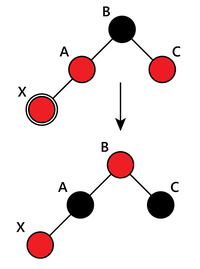
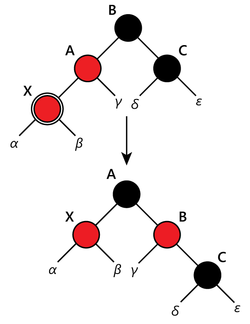
- "Дядя" чёрный. Если выполнить только перекрашивание, то может нарушиться постоянство чёрной высоты дерева по всем ветвям. Поэтому выполняем поворот. Если добавляемый узел был правым потомком, то необходимо сначала выполнить левое вращение, которое сделает его левым потомком. Таким образом, свойство и постоянство черной высоты сохраняются.
Псевдокод:
func insert(key)
Node t = Node(key, red, nil, nil) // конструктор, в который передаем ключ, цвет, левого и правого ребенка
if дерево пустое
root = t
t.parent = nil
else
Node p = root
Node q = nil
while p != nil // спускаемся вниз, пока не дойдем до подходящего листа
q = p
if p.key < t.key
p = p.right
else
p = p.left
t.parent = q
// добавляем новый элемент красного цвета
if q.key < t.key
q.right = t
else
q.left = t
fixInsertion(t) // проверяем, не нарушены ли свойства красно-черного дерева
func fixInsertion(t: Node)
if t — корень
t = black
return
// далее все предки упоминаются относительно t
while "отец" красный // нарушается свойство
if "отец" — левый ребенок
if есть красный "дядя"
parent = black
uncle = black
grandfather = red
t = grandfather
else
if t — правый сын
t = parent
leftRotate(t)
parent = black
grandfather = red
rightRotate(grandfather)
else // "отец" — правый ребенок
if есть красный "дядя"
parent = black
uncle = black
grandfather = red
t = grandfather
else // нет "дяди"
if t — левый ребенок
t = t.parent
rightRotate(t)
parent = black
grandfather = red
leftRotate(grandfather)
root = black // восстанавливаем свойство корня
Удаление вершины
При удалении вершины могут возникнуть три случая в зависимости от количества её детей:
- Если у вершины нет детей, то изменяем указатель на неё у родителя на .
- Если у неё только один ребёнок, то делаем у родителя ссылку на него вместо этой вершины.
- Если же имеются оба ребёнка, то находим вершину со следующим значением ключа. У такой вершины нет левого ребёнка (так как такая вершина находится в правом поддереве исходной вершины и она самая левая в нем, иначе бы мы взяли ее левого ребенка. Иными словами сначала мы переходим в правое поддерево, а после спускаемся вниз в левое до тех пор, пока у вершины есть левый ребенок). Удаляем уже эту вершину описанным во втором пункте способом, скопировав её ключ в изначальную вершину.
Проверим балансировку дерева. Так как при удалении красной вершины свойства дерева не нарушаются, то восстановление балансировки потребуется только при удалении чёрной. Рассмотрим ребёнка удалённой вершины.
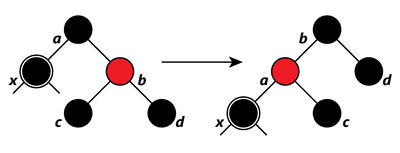
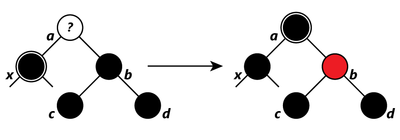
- Если брат этого ребёнка красный, то делаем вращение вокруг ребра между отцом и братом, тогда брат становится родителем отца. Красим его в чёрный, а отца — в красный цвет, сохраняя таким образом черную высоту дерева. Хотя все пути по-прежнему содержат одинаковое количество чёрных узлов, сейчас имеет чёрного брата и красного отца. Таким образом, мы можем перейти к следующему шагу.
- Если брат текущей вершины был чёрным, то получаем три случая:
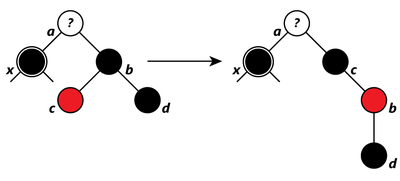
- Оба ребёнка у брата чёрные. Красим брата в красный цвет и рассматриваем далее отца вершины. Делаем его черным, это не повлияет на количество чёрных узлов на путях, проходящих через , но добавит один к числу чёрных узлов на путях, проходящих через , восстанавливая тем самым влиянние удаленного чёрного узла. Таким образом, после удаления вершины черная глубина от отца этой вершины до всех листьев в этом поддереве будет одинаковой.
- Если у брата правый ребёнок чёрный, а левый красный, то перекрашиваем брата и его левого сына и делаем вращение. Все пути по-прежнему содержат одинаковое количество чёрных узлов, но теперь у есть чёрный брат с красным правым потомком, и мы переходим к следующему случаю. Ни , ни его отец не влияют на эту трансформацию.
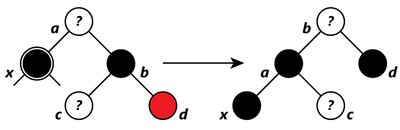
- Если у брата правый ребёнок красный, то перекрашиваем брата в цвет отца, его ребёнка и отца — в чёрный, делаем вращение. Поддерево по-прежнему имеет тот же цвет корня, поэтому свойство и не нарушаются. Но у теперь появился дополнительный чёрный предок: либо стал чёрным, или он и был чёрным и был добавлен в качестве чёрного дедушки. Таким образом, проходящие через пути проходят через один дополнительный чёрный узел. Выходим из алгоритма.
Продолжаем тот же алгоритм, пока текущая вершина чёрная и мы не дошли до корня дерева. Из рассмотренных случаев ясно, что при удалении выполняется не более трёх вращений.
Псевдокод:
func delete(key)
Node p = root
// находим узел с ключом key
while p.key != key
if p.key < key
p = p.right
else
p = p.left
if у p нет детей
if p — корень
root = nil
else
ссылку на p у "отца" меняем на nil
return
Node y = nil
Node q = nil
if один ребенок
ссылку на у от "отца" меняем на ребенка y
else
// два ребенка
y = вершина, со следующим значением ключа // у нее нет левого ребенка
if y имеет правого ребенка
y.right.parent = y.parent
if y — корень
root = y.right
else
у родителя ссылку на y меняем на ссылку на первого ребенка y
if y != p
p.colour = y.colour
p.key = y.key
if y.colour == black
// при удалении черной вершины могла быть нарушена балансировка
fixDeleting(q)
func fixDeleting(p: Node)
// далее родственные связи относительно p
while p — черный узел и не корень
if p — левый ребенок
if "брат" красный
brother = black
parent = red
leftRotate(parent)
if у "брата" черные дети // случай "брат" красный с черными детьми
brother = red
else
if правый ребенок "брата" черный // случай, рассматриваемый во втором подпункте:
brother.left = black // "брат" красный с черными правым ребенком
brother = red
rightRotate(brother)
brother.colour = parent.colour // случай, рассматриваемый в последнем подпункте
parent = black
brother.right = black
leftRotate(parent)
p = root
else // p — правый ребенок
// все случаи аналогичны тому, что рассмотрено выше
if "брат" красный
brother = black
parent = red
rightRotate(p.parent)
if у "брата" черные дети
brother = red
else
if левый ребенок "брата" черный
brother.right = black
brother = red
leftRotate(brother);
brother = parent
parent = black
brother.left = black
rightRotate(p.parent)
p = root
p = black
root = black
Объединение красно-чёрных деревьев
Объединение двух красно-чёрных деревьев и по ключу возвращает дерево с элементами из $T_2$, $T_1$ и $k$. Требование: ключ $k$ — разделяющий. То есть $\forall k_1\in T_1, k_2 \in T_2: k_1\leqslant k\leqslant k_2$.
Если оба дерева имеют одинаковую черную высоту, то результатом будет дерево с черным корнем $k$, левым и правым поддеревьями $k_1$ и $k_2$ соответствено.
Теперь пусть у $T_1$ черная высота больше (иначе аналогично).
- Находим в дереве $T_1$ вершину $y$ на черной высоте, как у дерева $T_2$ вершину с максимальным ключом. Это делается несложно (особенно если мы знаем черную высоту дерева): спускаемся вниз, поддерживая текущую черную высоту.
- Идем вправо. Когда высота станет равной высоте $T_2$, остановимся.
- Заметим, что черная высота $T_2\geqslant 2$. Поэтому в дереве $T_1$ мы не будем ниже, чем $2$. Пусть мы не можем повернуть направо (сын нулевой), тогда наша высота $2$ (если мы в черной вершине) или $1$ (если в красной). Второго случая быть не может, ибо высота $T_2\geqslant 2$, а в первом случае мы должны были завершить алгоритм, когда пришли в эту вершину.
- Очевидно, мы окажемся в черной вершине (ибо следующий шаг даст высоту меньше). Очевидно, мы оказались на нужной высоте.
- Теперь пусть мы попали не туда. То есть существует путь от корня до другой вершины. Посмотрим на то место, где мы не туда пошли. Если мы пошли вправо, а надо бы влево, то $x$ имеет больший ключ (по свойству дерева поиска). А если пошли влево, а не вправо, значит правого сына и нет (точнее, есть, но он нулевой), значит в правом поддереве вообще нет вершин.
- Более того, все вершины с высотами меньше $y$, которые имеют ключ больше $y$, будут находиться в поддереве $y$. Действительно, мы всегда идем вправо. Инвариант алгоритма на каждом шаге — в поддереве текущей вершины содержатся все вершины, ключ которых больше текущего. Проверяется очевидно.
- Еще поймем, как будем хранить черную высоту дерева. Изначально она нулевая (в пустом дереве). Далее просто поддерживаем ее при операциях вставки и удаления.
- Объединим поддерево. $k$ будет корнем, левым и правым сыновьями будут $T_y$ и $T_2$ соответственно.
- Покажем, что свойства дерева поиска не нарушены.
- Так как все ключи поддерева $y$ не более $k$ и все ключи $T_2$ не менее $k$, то в новом поддереве с корнем $k$ свойства выполняются.
- Так как $k$ больше любого ключа из $T_1$, то выполняется и для всего дерева.
- Красим $k$ в красный цвет. Тогда свойство $4$ будет выполнено. Далее поднимаемся вверх, как во вставке операциях, поворотами исправляя нарушение правила $3$.
- В конце корень красим в черный, если до этого был красный (это всегда можно сделать, ничего не нарушив).
Псевдокод:
func join(T_1, T_2, k)
if черные высоты равны
return Node(k, black, T_1, T_2)
if высота T_1 больше
T' = joinToRight(T_1, T_2, k)
T'.color = black
return T'
else
T' = joinToLeft(T_1, T_2, k)
T'.color = black
return T'
func joinToRight(T_1, T_2, k)
Y = find(T_1, bh(T_2))
T' = Node(k, red, Y, T_2)
while нарушение
действуем как во вставке
return T'
func find(T, h)
curBH = bh(T)
curV = T
while curBH != h
curV = curV.right
if curV.color == black
--curBH
return curV
Сложность: $\mathcal{O}(T_1.h-T_2.h)=\mathcal{O}(\log(n))$
Разрезание красно-чёрного дерева
Разрезание дерева по ключу $k$ вернет два дерева, ключи первого меньше $k$, а второго — не меньше.
Пройдем вниз как во время поиска. Все левые поддеревья вершин пути, корень которых не в пути, будут в первом поддереве. Аналогично правые — в правом. Теперь поднимаемся и последовательно сливаем деревья справа и слева с ответами.
За счет того, что функция $join$ работает за разницу высот, и мы объединяем снизу, то, благодаря телескопическому эффекту на работу времени будут влиять только крайние слагаемые, которые порядка глубины дерева.
Псевдокод
func split(T, k)
if T = nil
return $\langle$nil, nil$\rangle$
if k < T.key
$\langle$L',R'$\rangle$ = split(L,k)
return $\langle$L',join(R',T.key,R)$\rangle$
else
$\langle$L',R'$\rangle$ = split(R,k)
return $\langle$join(L,T.key,L'),R)$\rangle$
Сложность: $\mathcal{O}(\log(n))$
Точно такой же алгоритм в разрезании AVL деревьев. Оно и понятно — нам нужна лишь корректная функция $join$, работающая за разницу высот.
Преимущества красно-чёрных деревьев
- Самое главное преимущество красно-черных деревьев в том, что при вставке выполняется не более вращений. Это важно, например, в алгоритме построения динамической выпуклой оболочки. Ещё важно, что примерно половина вставок и удалений произойдут задаром.
- Процедуру балансировки практически всегда можно выполнять параллельно с процедурами поиска, так как алгоритм поиска не зависит от атрибута цвета узлов.
- Сбалансированность этих деревьев хуже, чем у АВЛ, но работа по поддержанию сбалансированности в красно-чёрных деревьях обычно эффективнее. Для балансировки красно-чёрного дерева производится минимальная работа по сравнению с АВЛ-деревьями.
- Использует всего $1$ бит дополнительной памяти для хранения цвета вершины. Но на самом деле в современных вычислительных системах память выделяется кратно байтам, поэтому это не является преимуществом относительно, например, АВЛ-дерева, которое хранит $2$ бита. Однако есть реализации красно-чёрного дерева, которые хранят значение цвета в бите. Пример — Boost Multiindex. В этой реализации уменьшается потребление памяти красно-чёрным деревом, так как бит цвета хранится не в отдельной переменной, а в одном из указателей узла дерева.
Красно-чёрные деревья являются наиболее активно используемыми на практике самобалансирующимися деревьями поиска. В частности, ассоциативные контейнеры библиотеки STL(map, set, multiset, multimap) основаны на красно-чёрных деревьях. TreeMap в Java тоже реализован на основе красно-чёрных деревьев.
Связь с 2-3 и 2-4 деревьями
Изоморфизм деревьев
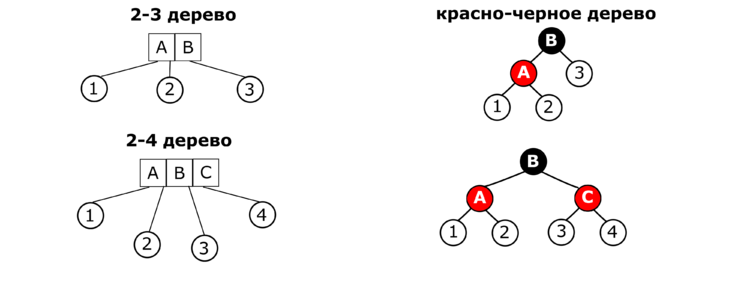
Красно-черные деревья изоморфны B-деревьям $4$ порядка. Реализация B-деревьев трудна на практике, поэтому для них был придуман аналог, называемый симметричным бинарным B-деревом[1]. Особенностью симметричных бинарных B-деревьев является наличие горизонтальных и вертикальных связей. Вертикальные связи отделяют друг от друга разные узлы, а горизонтальные соединяют элементы, хранящиеся в одном узле B-дерева. Для различения вертикальных и горизонтальных связей вводится новый атрибут узла — цвет. Только один из элементов узла в B-дереве красится в черный цвет. Горизонтальные связи ведут из черного узла в красный узел, а вертикальные могут вести из любого узла в черный.
Корректность сопоставления деревьев
Сопоставив таким образом цвета узлам дерева, можно проверить, что полученное дерево удовлетворяет всем свойствам красно-черного дерева.
| Утверждение: |
У красного узла родитель не может быть красного цвета. |
| В узле 2-4 дерева содержится не более трех элементов, один из которых обязательно красится в черный при переходе к симметричному бинарному B-дереву. Тогда оставшиеся красные элементы, если они есть, подвешиваются к черному. Из этих элементов могут идти ребра в следующий узел 2-4 дерева. В этом узле обязательно есть черная вершина, в нее и направляется ребро. Оставшиеся элементы узла, если они есть, подвешиваются к черной вершине аналогично первому узлу. Таким образом, ребро из красной вершины никогда не попадает в красную, значит у красного элемента родитель не может быть красным. |
| Утверждение: |
Число черных узлов на любом пути от листа до вершины одинаково. |
| В B-дереве глубина всех листьев одинакова, следовательно, одинаково и количество внутренних узлов на каждом пути. Мы сопоставляем чёрный цвет одному элементу внутреннего узла B-дерева. Значит, количество чёрных элементов на любом пути от листа до вершины одинаково. |
| Утверждение: |
Корень дерева — черный. |
| Если в корне один элемент, то он — чёрный. Если же в корне несколько элементов, то заметим, что один элемент окрашен в чёрный цвет, остальные — в красный. Горизонтальные связи, соединяющие элементы внутри одного узнала, ведут из чёрного элемента в красный, следовательно, красные элементы будут подвешены к чёрному. Он и выбирается в качестве корня симметричного бинарного B-дерева. |
Сопоставление операций в деревьях
Все операции, совершаемые в B-дереве, сопоставляются операциям в красно-черном дереве. Для этого достаточно доказать, что изменение узла в B-дереве соответствует повороту в красно-черном дереве.
| Утверждение: |
Изменение узла в B-дереве соответствует повороту в красно-черном дереве. |
|
В 2-4 дереве изменение узла необходимо при добавлении к нему элемента. Рассмотрим, как будет меняться структура B-дерева и, соответственно, красно-черного дерева при добавлении элемента:
|
| Теорема: |
Приведенное выше сопоставление B-деревьев и красно-черных деревьев является изоморфизмом. |
| Доказательство: |
| Доказательство следует непосредственно из приведенных выше утверждений. |