Карманная сортировка — различия между версиями
м (rollbackEdits.php mass rollback) |
|||
| (не показано 50 промежуточных версий 7 участников) | |||
| Строка 1: | Строка 1: | ||
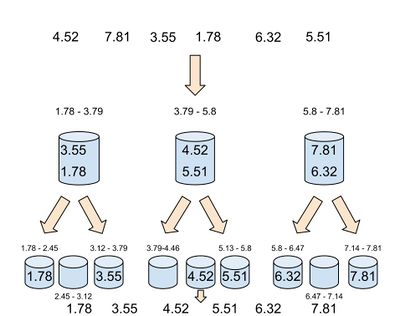
| + | [[Файл:Bucket-sort-example1.jpg|right|400px|thumb|Пример работы рекурсивного Bucketsort.]] | ||
| + | '''Карманная сортировка''' (англ. ''Bucket sort'') {{---}} алгоритм [[Сортировки|сортировки]], основанный на предположении о равномерном распределении входных данных. | ||
| + | == Алгоритм сортировки == | ||
| + | === Принцип работы === | ||
| + | Для карманной сортировки нужно разбить элементы массива входных данных на <tex>k</tex> блоков (карманов, корзин). Далее каждый из таких блоков сортируется либо другой сортировкой, либо рекурсивно тем же методом разбиения. После сортировок внутри каждых блоков данные записываются в массив в порядке разбиения на блоки. При этом нужно учитывать, что данная сортировка работает только в том случае, если разбиение на блоки производится таким образом, чтобы элементы каждого следующего блока были больше предыдущего. | ||
| + | |||
| + | Карманная сортировка сильно деградирует при большом количестве мало отличных элементов (большинство элементов попадёт в одну корзину). Поэтому такой тип сортировки использовать, когда велика вероятность того, что числа редко повторяются (например, последовательность случайных чисел). | ||
| + | |||
| + | === Реализация === | ||
| + | Существует несколько разных реализаций карманной сортировки. | ||
| + | |||
| + | Рассмотрим рекурсивную и нерекурсивную реализации. | ||
| + | ==== Рекурсивный bucket sort ==== | ||
| + | Рассмотрим код работы рекурсивной реализации карманной сортировки. | ||
| − | ''' | + | На вход подаются вещественные числа. |
| − | == | + | '''double[]''' bucketSort ('''double[]''' array, '''double''' minElement, '''double''' maxElement) |
| − | === | + | '''if''' array.length < 2 '''or''' minElement == maxElement |
| − | + | '''return''' array; | |
| − | + | range = maxElement - minElement | |
| − | + | '''for''' i = 0 '''to''' array.length - 1 | |
| − | + | index = int(array[i] * numBuckets / range) | |
| − | === | + | добавим array[i] в конец buckets[index] |
| − | + | minBucktes[index] = '''minimum'''(buckets[index], array[i]) | |
| − | + | maxBuckets[index] = '''maximum'''(buckets[index], array[i]) | |
| − | + | '''for''' i = 0 '''to''' numBuckets - 1 | |
| − | + | buckets[i] = bucketSort(buckets[i], minBucktes[i], maxBuckets[i]) | |
| − | + | '''for''' i = 0 '''to''' numBuckets - 1 | |
| − | + | '''for''' k = 0 '''to''' buckets[i].length - 1 | |
| − | + | добавим buckets[i][k] в конец answer | |
| − | + | '''return''' answer | |
| − | + | ||
| − | + | ==== Нерекурсивная реализация ==== | |
| − | + | '''double[]''' bucketSort('''double[]''' array) | |
| − | + | minElement = Infinum | |
| − | + | maxElement = -Infinum | |
| − | buckets[i] = | + | '''for''' i = 0 '''to''' array.length - 1 |
| − | + | minElement = '''minimum'''(minElement, array[i]) | |
| − | + | maxElement = '''maximum'''(maxElement, array[i]) | |
| − | for k = 0 to buckets[i].length | + | range = maxElement - minElement |
| − | + | '''for''' i = 0 '''to''' array.length - 1 | |
| − | + | index = int(array[i] * numBuckets / range) | |
| − | + | добавим array[i] в конец buckets[index] | |
| + | '''for''' i = 0 '''to''' numBuckets - 1 | ||
| + | buckets[i] = sort(buckets[i]) | ||
| + | '''for''' i = 0 '''to''' numBuckets - 1 | ||
| + | '''for''' k = 0 '''to''' buckets[i].length - 1 | ||
| + | добавим buckets[i][k] в конец answer | ||
| + | '''return''' answer | ||
| + | |||
| + | ==Асимптотика== | ||
| + | Пусть <tex>n</tex> {{---}} количество элементов в массиве, <tex>k</tex> {{---}} количество блоков для разбиения. | ||
| + | |||
| + | <tex> n_i </tex> {{---}} случайная величина, обозначающая количество элементов попавших в <tex> i </tex>-ый карман. | ||
| + | |||
| + | <tex> T(n) = \Theta(n) + \sum\limits_{i = 1}^k O(n_i</tex> <tex> \log n_i) + \Theta(k)</tex>, где <tex> T(n) </tex> время работы алгоритма карманной сортировки. | ||
| − | + | <tex> E[n_i] = \dfrac {n}{k} </tex> | |
| − | </ | ||
| − | |||
| − | |||
| + | То есть, если <tex> n \sim k \Rightarrow E[T(n)] = \Theta(n) </tex> | ||
| − | == | + | Если, <tex> n = o(k) \Rightarrow E[T(n)] = \Theta(k)</tex> |
| + | Из приведенных выше формул, видно, что в среднем "карманная сортировка" работает за линейное время. | ||
| + | ==Источники информации== | ||
| + | * [http://en.wikipedia.org/wiki/Bucket_sort Wikipedia — Bucket sort] | ||
| + | * [http://ru.wikipedia.org/wiki/%D0%91%D0%BB%D0%BE%D1%87%D0%BD%D0%B0%D1%8F_%D1%81%D0%BE%D1%80%D1%82%D0%B8%D1%80%D0%BE%D0%B2%D0%BA%D0%B0 Википедия — Блочная сортировка] | ||
| + | |||
| + | * [http://www.google.ru/url?sa=t&rct=j&q=&esrc=s&source=web&cd=10&ved=0CI0BEBYwCQ&url=http%3A%2F%2Fcs.iupui.edu%2F~xkzou%2Fteaching%2FCS580%2FSortinginlineartime.ppt&ei=d7fUT8WWIs3S4QSkkPT-Ag&usg=AFQjCNEUbmlVNhSgrJKV9-QjPBwU6U0obQ&sig2=3yaysrpuwVjmyhjBCpyBeQ Презентация о линейных сортировках] | ||
| + | * [https://www-927.ibm.com/ibm/cas/hspc/student/algorithms/BucketSort.html Описание алгоритма с реализацией рекурсивной версии на языке Java] | ||
[[Категория: Дискретная математика и алгоритмы]] | [[Категория: Дискретная математика и алгоритмы]] | ||
[[Категория: Сортировки]] | [[Категория: Сортировки]] | ||
| + | [[Категория: Другие сортировки]] | ||
Текущая версия на 19:15, 4 сентября 2022
Карманная сортировка (англ. Bucket sort) — алгоритм сортировки, основанный на предположении о равномерном распределении входных данных.
Содержание
Алгоритм сортировки
Принцип работы
Для карманной сортировки нужно разбить элементы массива входных данных на блоков (карманов, корзин). Далее каждый из таких блоков сортируется либо другой сортировкой, либо рекурсивно тем же методом разбиения. После сортировок внутри каждых блоков данные записываются в массив в порядке разбиения на блоки. При этом нужно учитывать, что данная сортировка работает только в том случае, если разбиение на блоки производится таким образом, чтобы элементы каждого следующего блока были больше предыдущего.
Карманная сортировка сильно деградирует при большом количестве мало отличных элементов (большинство элементов попадёт в одну корзину). Поэтому такой тип сортировки использовать, когда велика вероятность того, что числа редко повторяются (например, последовательность случайных чисел).
Реализация
Существует несколько разных реализаций карманной сортировки.
Рассмотрим рекурсивную и нерекурсивную реализации.
Рекурсивный bucket sort
Рассмотрим код работы рекурсивной реализации карманной сортировки.
На вход подаются вещественные числа.
double[] bucketSort (double[] array, double minElement, double maxElement)
if array.length < 2 or minElement == maxElement
return array;
range = maxElement - minElement
for i = 0 to array.length - 1
index = int(array[i] * numBuckets / range)
добавим array[i] в конец buckets[index]
minBucktes[index] = minimum(buckets[index], array[i])
maxBuckets[index] = maximum(buckets[index], array[i])
for i = 0 to numBuckets - 1
buckets[i] = bucketSort(buckets[i], minBucktes[i], maxBuckets[i])
for i = 0 to numBuckets - 1
for k = 0 to buckets[i].length - 1
добавим buckets[i][k] в конец answer
return answer
Нерекурсивная реализация
double[] bucketSort(double[] array)
minElement = Infinum
maxElement = -Infinum
for i = 0 to array.length - 1
minElement = minimum(minElement, array[i])
maxElement = maximum(maxElement, array[i])
range = maxElement - minElement
for i = 0 to array.length - 1
index = int(array[i] * numBuckets / range)
добавим array[i] в конец buckets[index]
for i = 0 to numBuckets - 1
buckets[i] = sort(buckets[i])
for i = 0 to numBuckets - 1
for k = 0 to buckets[i].length - 1
добавим buckets[i][k] в конец answer
return answer
Асимптотика
Пусть — количество элементов в массиве, — количество блоков для разбиения.
— случайная величина, обозначающая количество элементов попавших в -ый карман.
, где время работы алгоритма карманной сортировки.
То есть, если
Если,
Из приведенных выше формул, видно, что в среднем "карманная сортировка" работает за линейное время.