Алгоритм Киркпатрика детализации триангуляции — различия между версиями
Smolcoder (обсуждение | вклад) (→Псевдокод) |
м (rollbackEdits.php mass rollback) |
||
| (не показано 10 промежуточных версий 6 участников) | |||
| Строка 1: | Строка 1: | ||
==Мотивация== | ==Мотивация== | ||
| − | Существует ли метод локализации со временем поиска за <tex>O(\log n)</tex>, использующий менее чем квадратичную память? Эта задача оставалась не решенной довольно долго. Но все же была решена Липтоном и Тарьяном в 1977-1980 гг. Но их метод оказался | + | Существует ли метод локализации со временем поиска за <tex>O(\log n)</tex>, использующий менее чем квадратичную память? Эта задача оставалась не решенной довольно долго. Но все же была решена Липтоном и Тарьяном в 1977-1980 гг. Но их метод оказался настолько громоздким, а оценки времени его эффективности содержат слишком большую константу, что сами авторы не считали этот метод практичным, но его существование заставляет думать, что может найтись практичный алгоритм с временной оценкой <tex>O(\log n)</tex> и линейной памятью. |
Недавно Киркпатриком был предложен оптимальный метод, дающий ответ на ожидания Липтона и Тарьяна, {{---}} детализация триангуляции. | Недавно Киркпатриком был предложен оптимальный метод, дающий ответ на ожидания Липтона и Тарьяна, {{---}} детализация триангуляции. | ||
| Строка 6: | Строка 6: | ||
==Описание алгоритма== | ==Описание алгоритма== | ||
===Предобработка=== | ===Предобработка=== | ||
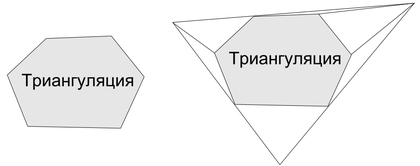
| − | <wikitex>[[Файл:кирк1.png|right| | + | <wikitex>[[Файл:кирк1.png|right|420px|thumb|Триангуляция в охватывающем треугольнике.]]Пусть планарный N-вершинный граф задает триангуляцию нашего многоугольника (если это не так, то воспользуемся методом триангуляции многоугольника за время $O (n \log n)$. Напомним, что триангуляция на множестве вершин $V$ есть планарный граф с не более чем $3 |V| - 6$ ребрами ([[Формула_Эйлера |формула Эйлера]]). Для удобства описания алгоритма поместим нашу триангуляцию в охватывающий треугольник и построим триангуляцию области между нашими объектами. После этого преобразования все триангуляции будут обладать тремя границами и ровно $3 |V| - 6$ ребрами. |
</wikitex> | </wikitex> | ||
| − | |||
===Структура данных=== | ===Структура данных=== | ||
| Строка 28: | Строка 27: | ||
Для ясности удобно изобразить $T$ в рассмотренном виде, то есть помещая его узлы в горизонтальные строки, каждая из | Для ясности удобно изобразить $T$ в рассмотренном виде, то есть помещая его узлы в горизонтальные строки, каждая из | ||
| − | которых соответствует какой-нибудь триангуляции. Последовательность триангуляций и соответствующая ей структура $T$ показаны на рисунке. Кружком обведены вершины, которые удалены на данном шаге. | + | которых соответствует какой-нибудь триангуляции. Последовательность триангуляций и соответствующая ей структура $T$ показаны на рисунке. Треугольники пронумерованы в порядке их появления. Кружком обведены вершины, которые удалены на данном шаге. </wikitex> |
====Выбор множества удаляемых вершин==== | ====Выбор множества удаляемых вершин==== | ||
| − | Как уже упоминалось, от выбора множества | + | <wikitex>Как уже упоминалось, от выбора множества вершин триангуляции, которые будут удалены при построении $S_i$ по $S_{i-1}$ существенно зависит эффективность метода. Предположим, что можно выбрать это множество так, чтобы выполнялись следующие ''свойства'' ($N_i$ обозначает число вершин в $S_i$): |
'''Свойство 1'''. $N_i = a_i N_{i-1}$, где $a_i \le a < 1$ для $i = 2,\dots , h(N)$. | '''Свойство 1'''. $N_i = a_i N_{i-1}$, где $a_i \le a < 1$ для $i = 2,\dots , h(N)$. | ||
'''Свойство 2'''. Каждый треугольник $R_i \in S_i$ пересекается не более чем с $H$ треугольниками из $S_{i-1}$ и наоборот. | '''Свойство 2'''. Каждый треугольник $R_i \in S_i$ пересекается не более чем с $H$ треугольниками из $S_{i-1}$ и наоборот. | ||
| − | Первое свойство немедленно влечет за собой следствие, что $h(N) \le \left \lceil \log_{1/a}N \right \rceil = O(log N)$, поскольку при переходе от $S_{i-1} к $S_i$ удаляется по меньшей мере фиксированная доля вершин. | + | Первое свойство немедленно влечет за собой следствие, что $h(N) \le \left \lceil \log_{1/a}N \right \rceil = O(log N)$, поскольку при переходе от $S_{i-1}$ к $S_i$ удаляется по меньшей мере фиксированная доля вершин. |
Также из этих свойств следует, что память для $T$ равна $O(N)$. Действительно, заметим, что эта память используется для хранения узлов и указателей на их потомков. Из [[Формула_Эйлера|теоремы Эйлера]] о плоских графах следует, что $S_i$ содержит $F_i < 2N_i$ треугольников. Число узлов в $T$, представляющих треугольники из $S_i$, не превосходит $F_i$ (только те треугольники, которые действительно принадлежат $S_i$, появляются на соответствующем «ярусе» $T$). Отсюда следует, что общее число узлов в $T$ меньше, чем | Также из этих свойств следует, что память для $T$ равна $O(N)$. Действительно, заметим, что эта память используется для хранения узлов и указателей на их потомков. Из [[Формула_Эйлера|теоремы Эйлера]] о плоских графах следует, что $S_i$ содержит $F_i < 2N_i$ треугольников. Число узлов в $T$, представляющих треугольники из $S_i$, не превосходит $F_i$ (только те треугольники, которые действительно принадлежат $S_i$, появляются на соответствующем «ярусе» $T$). Отсюда следует, что общее число узлов в $T$ меньше, чем | ||
| Строка 50: | Строка 49: | ||
'''1. ''' Для проверки первого свойства воспользуемся некоторыми особенностями плоских графов. Из [[Формула_Эйлера | формулы Эйлера]] для плоских графов, в частном случае триангуляции, ограниченной тремя ребрами, следует, что число вершин $N$ и число ребер $e$ связаны соотношением | '''1. ''' Для проверки первого свойства воспользуемся некоторыми особенностями плоских графов. Из [[Формула_Эйлера | формулы Эйлера]] для плоских графов, в частном случае триангуляции, ограниченной тремя ребрами, следует, что число вершин $N$ и число ребер $e$ связаны соотношением | ||
$e = 3N - 6$. | $e = 3N - 6$. | ||
| − | Пока в триангнуляции есть внутренние вершины (в противном случае задача тривиальна), степень каждой из трех граничных вершин меньше трех. Поскольку существует $3N - 6$ ребер, а каждое ребро инцидентно двум вершинам, то сумма степеней всех вершин меньше $6N$. Отсюда сразу следует, что не менее $ \frac{N}{2}$ вершин имеет степень меньше 12. Следовательно, пусть $K = 12$. Пусть также $v$ {{---}} число выбранных вершин. Поскольку каждой из них инцидентно не более $K-1 = 11$ ребер, а три граничные вершины не выбираются, то мы имеем | + | Пока в триангнуляции есть внутренние вершины (в противном случае задача тривиальна), степень каждой из трех граничных вершин не меньше трех. Поскольку существует $3N - 6$ ребер, а каждое ребро инцидентно двум вершинам, то сумма степеней всех вершин меньше $6N$. Отсюда сразу следует, что не менее $ \frac{N}{2}$ вершин имеет степень меньше 12. Следовательно, пусть $K = 12$. Пусть также $v$ {{---}} число выбранных вершин. Поскольку каждой из них инцидентно не более $K-1 = 11$ ребер, а три граничные вершины не выбираются, то мы имеем |
$v \ge \left \lfloor \frac{1}{12}(\frac{N}{2} - 3) \right \rfloor $. | $v \ge \left \lfloor \frac{1}{12}(\frac{N}{2} - 3) \right \rfloor $. | ||
Следовательно, $a \cong 1 - \frac{1}{24} < 0,959 < 1$, что доказывает справедливость свойства 1. | Следовательно, $a \cong 1 - \frac{1}{24} < 0,959 < 1$, что доказывает справедливость свойства 1. | ||
| Строка 61: | Строка 60: | ||
</wikitex> | </wikitex> | ||
====Псевдокод==== | ====Псевдокод==== | ||
| − | <wikitex>Пусть все потомки узла $u$ из $T$ собраны в список successors(u), а triangle(u) обозначает треугольник, соответствующий узлу $u$. Тогда алгоритм поиска может выглядеть следующим образом: | + | <wikitex>Пусть все потомки узла $u$ из $T$ собраны в список successors(u), а triangle(u) обозначает треугольник, соответствующий узлу $u$. Тогда алгоритм поиска может выглядеть следующим образом: </wikitex> |
procedure localization(z) | procedure localization(z) | ||
if (z not in triangle(root)) | if (z not in triangle(root)) | ||
| Строка 74: | Строка 73: | ||
==Источники== | ==Источники== | ||
* Препарата Ф., Шеймос М. Вычислительная геометрия: Введение: Пер. с англ. {{---}} М.: Мир, 1989. {{---}} 478 с. {{---}} ISBN 5-03-001041-6 | * Препарата Ф., Шеймос М. Вычислительная геометрия: Введение: Пер. с англ. {{---}} М.: Мир, 1989. {{---}} 478 с. {{---}} ISBN 5-03-001041-6 | ||
| + | |||
| + | [[Категория: Вычислительная геометрия]] | ||
Текущая версия на 19:38, 4 сентября 2022
Содержание
Мотивация
Существует ли метод локализации со временем поиска за , использующий менее чем квадратичную память? Эта задача оставалась не решенной довольно долго. Но все же была решена Липтоном и Тарьяном в 1977-1980 гг. Но их метод оказался настолько громоздким, а оценки времени его эффективности содержат слишком большую константу, что сами авторы не считали этот метод практичным, но его существование заставляет думать, что может найтись практичный алгоритм с временной оценкой и линейной памятью.
Недавно Киркпатриком был предложен оптимальный метод, дающий ответ на ожидания Липтона и Тарьяна, — детализация триангуляции.
Описание алгоритма
Предобработка
<wikitex>Пусть планарный N-вершинный граф задает триангуляцию нашего многоугольника (если это не так, то воспользуемся методом триангуляции многоугольника за время $O (n \log n)$. Напомним, что триангуляция на множестве вершин $V$ есть планарный граф с не более чем $3 |V| - 6$ ребрами (формула Эйлера). Для удобства описания алгоритма поместим нашу триангуляцию в охватывающий треугольник и построим триангуляцию области между нашими объектами. После этого преобразования все триангуляции будут обладать тремя границами и ровно $3 |V| - 6$ ребрами.</wikitex>
Структура данных
<wikitex>Итак, имеется N-вершинная триангуляция $G$, и пусть строится последовательность триангуляций $S_1, S_2, \dots, S_{h(N)}$, где $S_1 = G$, а $S_i$ получается из $S_{i - 1}$ по следующим правилам:
- Шаг 1. Удалим некоторое количество неграничных и независимых (попарно несмежных друг с другом) вершин и инцидентные им ребра (от выбора этого множества напрямую зависит оптимальность алгоритма).
- Шаг 2. Построить триангуляцию получившихся в результате шага 1 многоугольников.
Таким образом $S_{h(N)}$ состоит из одного треугольника. Заметим, что все триангуляции имеют одну общую границу, так как удаляются только внутренние узлы. Далее, будем обозначать все треугольники как $R$, а также будем говорить, что треугольник $R_ij$ принадлежит триангуляции $S_i$, если он был создан на шаге (2) при построении этой триангуляции.
Теперь построим структуру данных $T$ для поиска. Эта структура представляет собой направленный ацикличный граф, вершинами которого будут наши треугольники. Определим эту структуру следующим образом: из треугольника $R_k$ будет вести ребро в треугольник $R_j$, если при построении $S_i$ из $S_{i-1}$ мы имеем
- $R_j$ удалятся из $S_{i - 1}$ на шаге (1)
- $R_k$ создается в $S_{i}$ на шаге (2)
- $R_j \cap R_k \ne \varnothing $
Очевидно, что треугольники из $S_1$ (и только они) не имеют исходящих ребер.
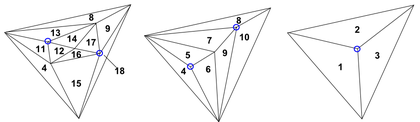
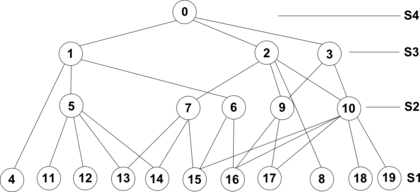
Для ясности удобно изобразить $T$ в рассмотренном виде, то есть помещая его узлы в горизонтальные строки, каждая из которых соответствует какой-нибудь триангуляции. Последовательность триангуляций и соответствующая ей структура $T$ показаны на рисунке. Треугольники пронумерованы в порядке их появления. Кружком обведены вершины, которые удалены на данном шаге. </wikitex>
Выбор множества удаляемых вершин
<wikitex>Как уже упоминалось, от выбора множества вершин триангуляции, которые будут удалены при построении $S_i$ по $S_{i-1}$ существенно зависит эффективность метода. Предположим, что можно выбрать это множество так, чтобы выполнялись следующие свойства ($N_i$ обозначает число вершин в $S_i$):
Свойство 1. $N_i = a_i N_{i-1}$, где $a_i \le a < 1$ для $i = 2,\dots , h(N)$.
Свойство 2. Каждый треугольник $R_i \in S_i$ пересекается не более чем с $H$ треугольниками из $S_{i-1}$ и наоборот. Первое свойство немедленно влечет за собой следствие, что $h(N) \le \left \lceil \log_{1/a}N \right \rceil = O(log N)$, поскольку при переходе от $S_{i-1}$ к $S_i$ удаляется по меньшей мере фиксированная доля вершин.
Также из этих свойств следует, что память для $T$ равна $O(N)$. Действительно, заметим, что эта память используется для хранения узлов и указателей на их потомков. Из теоремы Эйлера о плоских графах следует, что $S_i$ содержит $F_i < 2N_i$ треугольников. Число узлов в $T$, представляющих треугольники из $S_i$, не превосходит $F_i$ (только те треугольники, которые действительно принадлежат $S_i$, появляются на соответствующем «ярусе» $T$). Отсюда следует, что общее число узлов в $T$ меньше, чем $2(N_1 + N_2 + \dots + N_{h(N)}) \le 2N_1(1 + a + a^2 + \dots + a^{h(N) - 1}) < \frac{2N}{1 - a}$. Что касается памяти, используемой под указатели, то по свойству 2 каждый узел имеет не более $H$ указателей, поэтому не более $\frac{2NH}{1-a}$ указателей появится в $T$. Это доказывает последнее утверждение.
Покажем теперь, что критерий выбора множества удаляемых вершин, удовлетворяющий вышеописанным свойствам, существует.
| Теорема (критерий выбора множества удаляемых вершин): |
Если на шаге (1) построения последовательности триангуляции удалять несмежные вершины со степенью меньше некоторого целого (будет указано позже) числа $K$, то свойства, описанные выше, будут выполнены. |
| Доказательство: |
|
1. Для проверки первого свойства воспользуемся некоторыми особенностями плоских графов. Из формулы Эйлера для плоских графов, в частном случае триангуляции, ограниченной тремя ребрами, следует, что число вершин $N$ и число ребер $e$ связаны соотношением $e = 3N - 6$. Пока в триангнуляции есть внутренние вершины (в противном случае задача тривиальна), степень каждой из трех граничных вершин не меньше трех. Поскольку существует $3N - 6$ ребер, а каждое ребро инцидентно двум вершинам, то сумма степеней всех вершин меньше $6N$. Отсюда сразу следует, что не менее $ \frac{N}{2}$ вершин имеет степень меньше 12. Следовательно, пусть $K = 12$. Пусть также $v$ — число выбранных вершин. Поскольку каждой из них инцидентно не более $K-1 = 11$ ребер, а три граничные вершины не выбираются, то мы имеем $v \ge \left \lfloor \frac{1}{12}(\frac{N}{2} - 3) \right \rfloor $. Следовательно, $a \cong 1 - \frac{1}{24} < 0,959 < 1$, что доказывает справедливость свойства 1. 2. Выполнение второго свойства обеспечивается тривиально. Поскольку удаление вершины со степенью меньше $K$ приводит к образованию многоугольника с числом ребер менее $K$, то каждый из удаленных треугольников пересекает не более $K - 2 = H$ новых треугольников. |
Поиск
<wikitex>После построения структуры легко понять, как в ней происходит поиск. Элементарной операцией здесь является определение принадлежности треугольнику. Очевидно, что она выполняется константное время. Сначала мы локализуемся в треугольнике $S_1$. После этого мы строим путь от корневой вершины до листа следующим образом: находясь в какой-либо вершине $z$, просмотрим всех ее детей на принадлежность точки соответствующему треугольнику и, так как точка может находиться лишь в одном треугольнике конкретной триангуляции, перейдем в эту вершину, и продолжим поиск. Этот поиск также можно рассматривать как последовательную локализацию в триангуляциях $S_1, \dots, S_{h(N)}$, откуда и происходит название самого метода. </wikitex>
Псевдокод
<wikitex>Пусть все потомки узла $u$ из $T$ собраны в список successors(u), а triangle(u) обозначает треугольник, соответствующий узлу $u$. Тогда алгоритм поиска может выглядеть следующим образом: </wikitex>
procedure localization(z)
if (z not in triangle(root))
z in infinite region
else
u = root
while (successors(u) != null)
for (v in successors(u))
if (z in triangle(v))
u = v
return u
Источники
- Препарата Ф., Шеймос М. Вычислительная геометрия: Введение: Пер. с англ. — М.: Мир, 1989. — 478 с. — ISBN 5-03-001041-6