Алгоритм Ху-Таккера — различия между версиями
Kris (обсуждение | вклад) м |
м (rollbackEdits.php mass rollback) |
||
| (не показано 39 промежуточных версий 5 участников) | |||
| Строка 1: | Строка 1: | ||
| − | '''''Алгоритм | + | '''''Алгоритм Ху–Таккера''''' (англ. ''Hu–Tucker Algorithm'') {{---}} алгоритм построения оптимального алфавитного дерева. |
| − | ''Алфавитное дерево'' - дерево в котором при просмотре листьев слева направо символы идут в алфавитном порядке и код последующего лексикографически больше предыдущего. | + | {{Определение |
| − | + | |definition= | |
| + | '''Алфавитное дерево''' (англ. ''Alphabetical tree'') {{---}} дерево в котором при просмотре листьев слева направо символы идут в алфавитном порядке, и код последующего лексикографически больше предыдущего. | ||
| + | }} | ||
{{Определение | {{Определение | ||
|definition= | |definition= | ||
| − | Пусть <tex>A=\{a_{1},a_{2},...,a_{n}\}</tex> — алфавит из n различных символов, <tex>W=\{w_{1},w_{2},...,w_{n}\}</tex> — соответствующий ему набор весов. Тогда алгоритм выбора набора бинарных кодов <tex>C=\{c_{1},c_{2},...,c_{n}\}</tex>, такой, что: | + | Пусть <tex>A=\{a_{1},a_{2},...,a_{n}\}</tex> — алфавит из <tex>n</tex> различных символов, <tex>W=\{w_{1},w_{2},...,w_{n}\}</tex> — соответствующий ему набор весов. Тогда алгоритм выбора набора бинарных кодов <tex>C=\{c_{1},c_{2},...,c_{n}\}</tex>, такой, что: |
| − | + | *<tex>c_{i}</tex> не является префиксом для <tex>c_{j}</tex>, при <tex>i \ne j</tex>, | |
| − | + | *для всех <tex>a_{i}<a_{j}</tex> выполнено <tex>c_{i}<c_{j}</tex>, | |
| − | + | *при удовлетворенности условия <tex>2</tex>, <tex>\sum\limits_{i \in [1, n]} w_{i}\cdot |c_{i}|</tex> минимальна (<tex>|c_{i}|</tex> — длина кода <tex>c_{i}</tex>) | |
| − | называется ''алгоритмом | + | называется '''алгоритмом Ху–Таккера'''. |
}} | }} | ||
| + | |||
== Алгоритм == | == Алгоритм == | ||
| − | |||
| − | 1. ''Комбинирование''. По данной последовательности из n вершин строим последовательность из <tex>n-1</tex> вершины, комбинируя минимальную совместимую пару и заменяя ее левую вершину вершиной с весом <tex> w = w_{l} + w_{r} </tex> и удаляя правую. Эта процедура повторяется до тех пор пока не останется одна вершина. | + | === Алгоритм Ху–Таккера === |
| − | + | * Начало. | |
| − | + | * '''Шаг 0.''' ''Введем следующие понятия''. | |
| − | + | **Две вершины называются совместимой парой (англ. ''compatible pair''), если они соседние или если между ними нет вершин алфавита. | |
| − | + | **Две вершины называются минимальной парой, когда их суммарный вес наименьший из всех. При равенстве весов выбирается пара с самой левой вершиной, из всех таких та, у которой правый узел расположен левее. | |
| + | **Минимальной совместимой парой называется наименьшая пара из всех совместимых. | ||
| + | * '''Шаг 1.''' Изначально мы имеем только алфавит (и соответствующие веса), отсортированный лексикографически. | ||
| + | * '''Шаг 2.''' ''Комбинирование'' (англ. ''Combining''). По данной последовательности из <tex>n</tex> вершин строим последовательность из <tex>n-1</tex> вершины, комбинируя минимальную совместимую пару и заменяя ее левую вершину вершиной с весом <tex> w = w_{l} + w_{r} </tex> и удаляя правую. Эта процедура повторяется до тех пор, пока не останется одна вершина. | ||
| + | * '''Шаг 3.''' ''Определение уровней''. Находим номер уровня <tex>l_{i}</tex> каждого листа относительно корня. | ||
| + | * '''Шаг 4.''' ''Перестройка''. После того, как номера уровней <tex>l_{1}, l_{2}, ..., l_{n}</tex> всех листьев определены, просматриваем последовательность слева направо и находим самый левый номер максимального уровня, скажем, <tex>l_{i}=q</tex>. Тогда и <tex>l_{i+1}=q</tex> (в последовательности <tex>l_{1}, l_{2}, ..., l_{n}</tex> максимальные номера уровней всегда располагаются рядом). Создаем вершину уровня <tex>q-1</tex> вместо вершин уровня <tex>q</tex>. Другими словами, последовательность уровней <tex>l_{1}, l_{2}, ..., l_{q}, l_{q}, ..., l_{n}</tex> заменяется на <tex>l_{1}, l_{2}, ..., l_{q}-1, ..., l_{n}</tex>. Повторяем этот процесс до тех пор пока не останется одна вершина с уровнем <tex>0</tex>. | ||
| + | * Конец. | ||
Заметим, что перестройку легко можно организовать с помощью следующего стекового алгоритма. | Заметим, что перестройку легко можно организовать с помощью следующего стекового алгоритма. | ||
| − | + | === Стековый алгоритм перестройки === | |
| − | Шаг 0. Стек пуст. | + | * Начало. |
| − | + | * '''Шаг 0.''' [[Стек]] пуст. | |
| − | Шаг 1. Если значение двух верхних элементов различно или в стеке всего один элемент перейти к шагу 2, иначе шагу 3. | + | * '''Шаг 1.''' Если значение двух верхних элементов различно или в стеке всего один элемент перейти к шагу <tex>2</tex>, иначе к шагу <tex>3</tex>. |
| − | + | * '''Шаг 2.''' Поместить следующий элемент <tex>l_{i}</tex> на вершину стека. Перейти к шагу <tex>1</tex>. | |
| − | Шаг 2. Поместить следующий элемент | + | * '''Шаг 3.''' Удалить <tex>2</tex> верхних элемента стека, поместить в стек элемент со значением меньшим на единицу, чем удаленные. Если значение нового элемента равно нулю {{---}} остановиться, иначе перейти к шагу <tex>1</tex>. |
| − | + | * Конец. | |
| − | Шаг 3. Удалить 2 верхних элемента стека, поместить в стек элемент со значением меньшим на единицу, чем удаленные | ||
==Пример== | ==Пример== | ||
| − | + | Для примера возьмем алфавит <tex>A= \{a,b,c,d,e,f,t,g,h,i,j\} </tex>, а набор весов <tex>W= \{8,6,2,3,4,7,11,9,8,1,3\} </tex>. | |
| − | Для примера возьмем алфавит <tex>A= \{ | ||
| − | Выполним | + | Выполним второй шаг алгоритма. |
| − | Объединим сначала <tex>i 1</tex> и <tex>j 3</tex>, получим вершину с весом <tex>ij 4</tex>, затем <tex>c 2</tex> и <tex>d 3</tex> на вершину веса <tex>cd 5</tex>, и т.д. пока не останется одна вершина. | + | Объединим сначала <tex>w_{i}=1</tex> и <tex>w_{j}=3</tex>, получим вершину с весом <tex>w_{ij}=4</tex>, затем <tex>w_{c}=2</tex> и <tex>w_{d}=3</tex> на вершину веса <tex>w_{cd}=5</tex>, и т.д. пока не останется одна вершина. |
| + | [[Файл:Hu-Taker_eps1.gif|300px]] | ||
| + | Выполним третий шаг. | ||
| + | Определим уровни для каждого листа <tex>L= \{3,3,5,5,4,3,3,3,3,4,4\} </tex>. | ||
| + | [[Файл:Hu-Taker Layer2.png|300px]] | ||
| + | Выполним четвертый шаг, воспользовавшись стековым алгоритмом, и получим необходимое дерево. | ||
| + | [[Файл:Hu-Taker_eps3.gif|300px]][[Файл:Hu Takker eps3.png |300px]] | ||
| + | Осталось только назначить код для каждого символа. Это делается аналогично [[Алгоритм Хаффмана|коду Хаффмана]]: левым ребрам назначается <tex>0</tex>, а правым <tex>1</tex>. | ||
| + | == Обоснование алгоритма Ху–Таккера == | ||
| + | Далее последовательностью–впадиной будем называть последовательность вида <tex>w_{1} > ... > w_{t} < ... < w_{n}</tex>. | ||
| + | Для обоснования воспользуемся несколькими леммами. | ||
| + | {{Лемма | ||
| + | |id=lemma1 | ||
| + | |about=1 | ||
| + | |statement= | ||
| + | Если последовательность весов монотонно не убывает или монотонно убывает, то стоимости деревьев Хаффмана и Ху–Таккера совпадают. Более того, существует дерево Хаффмана, удовлетворяющее требованию алфавитности (см. упражнения к разделу 2.3.4–5 вт.1 книги Д. Кнута Искусство программирования для ЭВМ). | ||
| + | }} | ||
| + | {{Лемма | ||
| + | |id=lemma2 | ||
| + | |about=2 | ||
| + | |statement= | ||
| + | Если последовательность весов является впадиной, то стоимости деревьев Хаффмана и Ху–Таккера равны. Более того, существует дерево Хаффмана, удовлетворяющее требованию алфавитности (см. книгу Т.Ч.Ху и М.Т.Шинг Комбинаторные алгоритмы {{---}} леммы 7 и 8 в разделе 5.8). | ||
| + | }} | ||
| + | {{Лемма | ||
| + | |id=lemma3 | ||
| + | |about=3 | ||
| + | |statement= | ||
| + | Если последовательность весов является впадиной, то новые вершины, создаваемые в фазе <tex>1</tex> алгоритма Ху–Таккера, образуют очередь с монотонно возрастающими весами. Потомки каждой из этих новых вершин могут быть соединены в алфавитное бинарное дерево (англ. ''Alphabetical binary tree''), удовлетворяющее условию: если <tex>w_{i} \leqslant w_{j}</tex>, то <tex>l_{j} \leqslant l_{i}</tex>. | ||
| + | }} | ||
| + | Заметим, что в последовательности-впадине две наименьших вершины всегда совместимы. Поэтому в алгоритме Хаффмана будут комбинироваться те же пары, что и в фазе <tex>1</tex> алгоритма Ху–Таккера. Для удобства введем две вершины алфавита <tex>w_{L}</tex> и <tex>w_{R}</tex> веса <tex>\infty</tex>, расположенных соответственно в начале и в конце последовательности. Тогда последовательность весов <tex>w_{1} < w_{2} < ... < w_{t} > w_{t+1} > ... > w_{n}</tex> можно рассматривать как последовательность состоящую из двух впадин: <tex>w_{L} > w_{1} < w_{2} < ... < w_{t} > w_{t+1} > ... > w_{n} < w_{R}</tex>. | ||
| + | Вершину <tex>t</tex> назовем горой между двумя впадинами. | ||
| + | Из [[#lemma3|леммы 3]] следует, что можно образовать две отдельных [[Очередь | очереди]] {{---}} одну для каждой впадины. Из-за горы вершины из разных впадин не совместимы между собой. Когда наименьшие новые вершины(полученные в результате слияния) во впадинах станут достаточно большими, гора будет наконец скомбинирована. С этого момента все новые вершины станут совместимыми. Получается слияние двух очередей. По существу, фаза <tex>1</tex> в алгоритме Ху–Таккера подобна слиянию нескольких очередей, а произвольную последовательность весов можно рассматривать как соединение нескольких впадин. | ||
| + | Чтобы понять, почему последовательность уровней может быть соединена в алфавитное дерево на третьем шаге алгоритма, достаточно рассмотреть два случая: | ||
| + | *Комбинируются две вершины из одной впадины. | ||
| + | *Комбинируются две вершины <tex>a</tex> и <tex>e</tex> из разных впадин. Пусть при этом между <tex>a</tex> и <tex>e</tex> расположены новые вершины <tex>b,c,d</tex> {{---}} каждая из них имеет двух сыновей, скажем, <tex>b1</tex> и <tex>b2</tex>, <tex>c1</tex> и <tex>c2</tex>, <tex>d1</tex> и <tex>d2</tex> {{---}} когда комбинируются <tex>a</tex> и <tex>e</tex>, мы в действительности создаем общего отца для <tex>a</tex> и <tex>b1</tex>. После этого общего отца получают <tex>b2</tex> и <tex>c1</tex>, затем <tex>c2</tex> и <tex>d1</tex>. Наконец, общего отца получают <tex>d2</tex> и <tex>e</tex>. | ||
| + | Заметим, что это лишь обоснование, а не строгое доказательство, его задача {{---}} дать понимание правдивости алгоритма. | ||
| − | + | == Корректность алгоритма Ху–Таккера == | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| + | Как пишет Д. Кнут короткого доказательства алгоритма не известно, и вероятно оно никогда не будет найдено. Для доказательства своего алгоритма Ху и Таккеру потребовалось <tex>3</tex> теоремы и <tex>2</tex> леммы (См. книгу Т.Ч.Ху и М.Т.Шинг Комбинаторные алгоритмы {{---}} стр.172). | ||
| + | == Сложность алгоритма == | ||
| + | Для реализации данного алгоритма потребуется <tex>O(n)</tex> памяти и <tex>O(n \log n)</tex> времени на построение дерева. | ||
| + | Разберем оценку. Для доказательства такой оценки времени введем понятие ''локально минимальной совместимой пары'' (л.м.с.п), пара <tex>(w_{l},w_{r})</tex> является л.м.с.п, когда выполнены следующие условия <tex>w_{r}<w_{i}</tex> для всех вершин <tex>i</tex> совместимых с <tex>l</tex> и <tex>w_{l} \leqslant w_{j}</tex> для всех вершин <tex>j</tex> совместимых с <tex>r</tex>. Также докажем следующую лемму: | ||
| + | {{Лемма | ||
| + | |id=lemma1 | ||
| + | |about=1 | ||
| + | |statement= | ||
| + | Пусть <tex>a</tex> {{---}} любая вершина в последовательности, состоящей из вершин алфавита и вершин, образованных в результате комбинации, <tex>w_{i}</tex> {{---}} вес наименьшей вершины <tex>i</tex>, совместимой с <tex>a</tex>. Если в результате комбинирования некоторой л.м.с.п. какая-нибудь новая вершина <tex>d</tex> становится совместимой с <tex>a</tex>, то <tex>w_{i}<w_{d}</tex>. В частности, в последовательности вершин будет оставаться л.м.с.п., пока комбинируются другие л.м.с.п. | ||
| + | Из этой леммы следует, что дерево, получаемое комбинированием л.м.с.п., не зависит от того, в каком порядке они комбинируются. | ||
| + | |proof= | ||
| + | Рассмотрим произвольную вершину <tex>a</tex> и предположим, что вес наименьшей вершины, совместимой с <tex>a</tex>, равен <tex>w_{i}</tex>. | ||
| + | Пусть комбинируется л.м.с.п. <tex>(b, c)</tex>, причем <tex>a</tex> ближе к <tex>b</tex>. Тогда между <tex>a</tex> и <tex>b</tex> нет вершин алфавита и хотя бы одна из <tex>b</tex>, <tex>c</tex> должна быть вершиной алфавита, иначе при слиянии <tex>(b, c)</tex> не появилось бы новых вершин (кроме <tex>bc</tex>), совместимых с <tex>a</tex>. | ||
| + | |||
| + | Заметим, что <tex>w_{i}</tex> может находиться в любой стороне от <tex>a</tex>. Если вершина <tex>w_{i}</tex> лежит справа от <tex>a</tex>, то она не вершина алфавита. Пусть <tex>d</tex> {{---}} вершина, которая становится совместимой с <tex>a</tex> после слияния <tex>(b, c)</tex> (она может быть как алфавитной так и слитой). Тогда <tex>d</tex> должна быть совместима с <tex>c</tex> в исходной последовательности и в силу локальной минимальности пары <tex>(b, c)</tex> имеем <tex>w_{b} \leqslant w_{d}</tex>. | ||
| + | Но <tex>w_{i}<w_{b}</tex>, так как <tex>b</tex> совместима с <tex>a</tex> в исходной последовательности, а <tex>w_{i}</tex> является наименьшим совместимым с <tex>a</tex> весом. Поэтому <tex>w_{i} \leqslant w_{b} \leqslant w_{d}</tex>. | ||
| + | Мы доказали, что вес наименьшей вершины, совместимой с любой вершиной, не может уменьшиться. Отсюда следует, что любая л.м.с.п. <tex>(x, y)</tex> останется л.м.с.п. после слияния другой л.м.с.п., потому что <tex>x</tex> останется наименьшей вершиной, совместимой с <tex>y</tex>, и наоборот. | ||
| + | }} | ||
| − | + | Теперь согласно этой лемме нам не придется искать минимально совместимую пару, что весьма долго. Достаточно лишь находить л.м.с.п., при этом не важно, в каком порядке комбинировать л.м.с.п. По этому нам необходимо иметь массив размера <tex>n</tex>, из которого мы будем удалять л.м.с.п и создавать новую вершину. На нем легко будет осуществлять поиск л.м.с.п. А так же необходим массив размера <tex>2n</tex> для реализации следующего шага, хранящий дерево. Второй шаг легко осуществить проходом по дереву, имея сохраненное дерево. Третий шаг, реализованный стековым алгоритмом, работает за <tex>2n</tex> времени и требует <tex>4n</tex> памяти <tex>n</tex> на стек, <tex>n</tex> на хранения уровней вершин и <tex>2n</tex> на хранение итогового дерева. Итак, общая оценка как раз получается <tex>O(n)</tex> памяти и <tex>O(n \log n)</tex> времени. | |
| − | [[ | + | == См. также == |
| + | * [[Алгоритм Хаффмана]] | ||
| + | * [[Избыточное кодирование, код Хэмминга]] | ||
| + | * [[Стек]] | ||
| + | * [[Очередь]] | ||
| − | + | == Источники информации == | |
| + | * ''Т.Ч.Ху, М.Т.Шинг'' Комбинаторные алгоритмы. — стр. 166. — ISBN 5-85746-761-6 | ||
| + | * ''Дональд Кнут'' Искусство программирования, том 3. Сортировка и поиск — 824 с. — ISBN 5-8459-0082-4 | ||
| − | |||
| − | + | [[Категория: Дискретная математика и алгоритмы]] | |
| − | + | [[Категория: Алгоритмы сжатия ]] | |
| − | |||
| − | |||
Текущая версия на 19:33, 4 сентября 2022
Алгоритм Ху–Таккера (англ. Hu–Tucker Algorithm) — алгоритм построения оптимального алфавитного дерева.
| Определение: |
| Алфавитное дерево (англ. Alphabetical tree) — дерево в котором при просмотре листьев слева направо символы идут в алфавитном порядке, и код последующего лексикографически больше предыдущего. |
| Определение: |
Пусть — алфавит из различных символов, — соответствующий ему набор весов. Тогда алгоритм выбора набора бинарных кодов , такой, что:
|
Алгоритм
Алгоритм Ху–Таккера
- Начало.
- Шаг 0. Введем следующие понятия.
- Две вершины называются совместимой парой (англ. compatible pair), если они соседние или если между ними нет вершин алфавита.
- Две вершины называются минимальной парой, когда их суммарный вес наименьший из всех. При равенстве весов выбирается пара с самой левой вершиной, из всех таких та, у которой правый узел расположен левее.
- Минимальной совместимой парой называется наименьшая пара из всех совместимых.
- Шаг 1. Изначально мы имеем только алфавит (и соответствующие веса), отсортированный лексикографически.
- Шаг 2. Комбинирование (англ. Combining). По данной последовательности из вершин строим последовательность из вершины, комбинируя минимальную совместимую пару и заменяя ее левую вершину вершиной с весом и удаляя правую. Эта процедура повторяется до тех пор, пока не останется одна вершина.
- Шаг 3. Определение уровней. Находим номер уровня каждого листа относительно корня.
- Шаг 4. Перестройка. После того, как номера уровней всех листьев определены, просматриваем последовательность слева направо и находим самый левый номер максимального уровня, скажем, . Тогда и (в последовательности максимальные номера уровней всегда располагаются рядом). Создаем вершину уровня вместо вершин уровня . Другими словами, последовательность уровней заменяется на . Повторяем этот процесс до тех пор пока не останется одна вершина с уровнем .
- Конец.
Заметим, что перестройку легко можно организовать с помощью следующего стекового алгоритма.
Стековый алгоритм перестройки
- Начало.
- Шаг 0. Стек пуст.
- Шаг 1. Если значение двух верхних элементов различно или в стеке всего один элемент перейти к шагу , иначе к шагу .
- Шаг 2. Поместить следующий элемент на вершину стека. Перейти к шагу .
- Шаг 3. Удалить верхних элемента стека, поместить в стек элемент со значением меньшим на единицу, чем удаленные. Если значение нового элемента равно нулю — остановиться, иначе перейти к шагу .
- Конец.
Пример
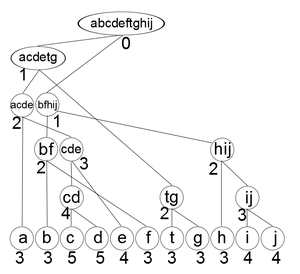
Для примера возьмем алфавит , а набор весов .
Выполним второй шаг алгоритма.
Объединим сначала и , получим вершину с весом , затем и на вершину веса , и т.д. пока не останется одна вершина.
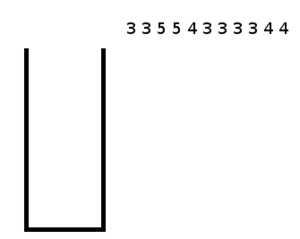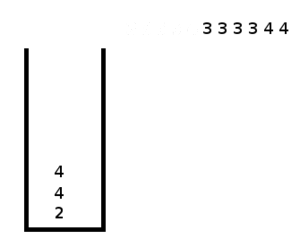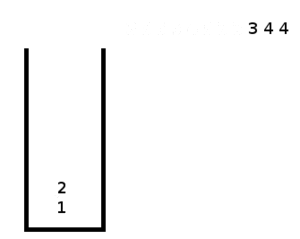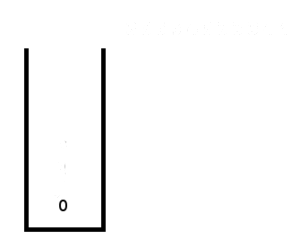
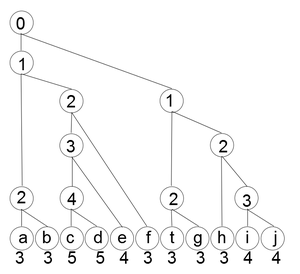
Выполним третий шаг. Определим уровни для каждого листа .
Выполним четвертый шаг, воспользовавшись стековым алгоритмом, и получим необходимое дерево.
Осталось только назначить код для каждого символа. Это делается аналогично коду Хаффмана: левым ребрам назначается , а правым .
Обоснование алгоритма Ху–Таккера
Далее последовательностью–впадиной будем называть последовательность вида .
Для обоснования воспользуемся несколькими леммами.
| Лемма (1): |
Если последовательность весов монотонно не убывает или монотонно убывает, то стоимости деревьев Хаффмана и Ху–Таккера совпадают. Более того, существует дерево Хаффмана, удовлетворяющее требованию алфавитности (см. упражнения к разделу 2.3.4–5 вт.1 книги Д. Кнута Искусство программирования для ЭВМ). |
| Лемма (2): |
Если последовательность весов является впадиной, то стоимости деревьев Хаффмана и Ху–Таккера равны. Более того, существует дерево Хаффмана, удовлетворяющее требованию алфавитности (см. книгу Т.Ч.Ху и М.Т.Шинг Комбинаторные алгоритмы — леммы 7 и 8 в разделе 5.8). |
| Лемма (3): |
Если последовательность весов является впадиной, то новые вершины, создаваемые в фазе алгоритма Ху–Таккера, образуют очередь с монотонно возрастающими весами. Потомки каждой из этих новых вершин могут быть соединены в алфавитное бинарное дерево (англ. Alphabetical binary tree), удовлетворяющее условию: если , то . |
Заметим, что в последовательности-впадине две наименьших вершины всегда совместимы. Поэтому в алгоритме Хаффмана будут комбинироваться те же пары, что и в фазе алгоритма Ху–Таккера. Для удобства введем две вершины алфавита и веса , расположенных соответственно в начале и в конце последовательности. Тогда последовательность весов можно рассматривать как последовательность состоящую из двух впадин: .
Вершину назовем горой между двумя впадинами.
Из леммы 3 следует, что можно образовать две отдельных очереди — одну для каждой впадины. Из-за горы вершины из разных впадин не совместимы между собой. Когда наименьшие новые вершины(полученные в результате слияния) во впадинах станут достаточно большими, гора будет наконец скомбинирована. С этого момента все новые вершины станут совместимыми. Получается слияние двух очередей. По существу, фаза в алгоритме Ху–Таккера подобна слиянию нескольких очередей, а произвольную последовательность весов можно рассматривать как соединение нескольких впадин.
Чтобы понять, почему последовательность уровней может быть соединена в алфавитное дерево на третьем шаге алгоритма, достаточно рассмотреть два случая:
- Комбинируются две вершины из одной впадины.
- Комбинируются две вершины и из разных впадин. Пусть при этом между и расположены новые вершины — каждая из них имеет двух сыновей, скажем, и , и , и — когда комбинируются и , мы в действительности создаем общего отца для и . После этого общего отца получают и , затем и . Наконец, общего отца получают и .
Заметим, что это лишь обоснование, а не строгое доказательство, его задача — дать понимание правдивости алгоритма.
Корректность алгоритма Ху–Таккера
Как пишет Д. Кнут короткого доказательства алгоритма не известно, и вероятно оно никогда не будет найдено. Для доказательства своего алгоритма Ху и Таккеру потребовалось теоремы и леммы (См. книгу Т.Ч.Ху и М.Т.Шинг Комбинаторные алгоритмы — стр.172).
Сложность алгоритма
Для реализации данного алгоритма потребуется памяти и времени на построение дерева.
Разберем оценку. Для доказательства такой оценки времени введем понятие локально минимальной совместимой пары (л.м.с.п), пара является л.м.с.п, когда выполнены следующие условия для всех вершин совместимых с и для всех вершин совместимых с . Также докажем следующую лемму:
| Лемма (1): |
Пусть — любая вершина в последовательности, состоящей из вершин алфавита и вершин, образованных в результате комбинации, — вес наименьшей вершины , совместимой с . Если в результате комбинирования некоторой л.м.с.п. какая-нибудь новая вершина становится совместимой с , то . В частности, в последовательности вершин будет оставаться л.м.с.п., пока комбинируются другие л.м.с.п.
|
| Доказательство: |
|
Рассмотрим произвольную вершину и предположим, что вес наименьшей вершины, совместимой с , равен . Пусть комбинируется л.м.с.п. , причем ближе к . Тогда между и нет вершин алфавита и хотя бы одна из , должна быть вершиной алфавита, иначе при слиянии не появилось бы новых вершин (кроме ), совместимых с . Заметим, что может находиться в любой стороне от . Если вершина лежит справа от , то она не вершина алфавита. Пусть — вершина, которая становится совместимой с после слияния (она может быть как алфавитной так и слитой). Тогда должна быть совместима с в исходной последовательности и в силу локальной минимальности пары имеем . Но , так как совместима с в исходной последовательности, а является наименьшим совместимым с весом. Поэтому . Мы доказали, что вес наименьшей вершины, совместимой с любой вершиной, не может уменьшиться. Отсюда следует, что любая л.м.с.п. останется л.м.с.п. после слияния другой л.м.с.п., потому что останется наименьшей вершиной, совместимой с , и наоборот. |
Теперь согласно этой лемме нам не придется искать минимально совместимую пару, что весьма долго. Достаточно лишь находить л.м.с.п., при этом не важно, в каком порядке комбинировать л.м.с.п. По этому нам необходимо иметь массив размера , из которого мы будем удалять л.м.с.п и создавать новую вершину. На нем легко будет осуществлять поиск л.м.с.п. А так же необходим массив размера для реализации следующего шага, хранящий дерево. Второй шаг легко осуществить проходом по дереву, имея сохраненное дерево. Третий шаг, реализованный стековым алгоритмом, работает за времени и требует памяти на стек, на хранения уровней вершин и на хранение итогового дерева. Итак, общая оценка как раз получается памяти и времени.
См. также
Источники информации
- Т.Ч.Ху, М.Т.Шинг Комбинаторные алгоритмы. — стр. 166. — ISBN 5-85746-761-6
- Дональд Кнут Искусство программирования, том 3. Сортировка и поиск — 824 с. — ISBN 5-8459-0082-4