Meet-in-the-middle — различия между версиями
Dronov (обсуждение | вклад) |
м (rollbackEdits.php mass rollback) |
||
| (не показаны 64 промежуточные версии 9 участников) | |||
| Строка 1: | Строка 1: | ||
{{Определение | {{Определение | ||
|definition= | |definition= | ||
| − | '''Meet-in-the-middle'' | + | '''Встреча в середине''' (англ. ''Meet-in-the-middle'') — это метод решения уравнения вида <tex> f({x}) = g({y}) </tex>, где <tex> x \in {X} </tex> и <tex> y \in {Y} </tex>, который работает за время <tex> O(F(X) + Y \times G_X(y))</tex>, где <tex> F(X) </tex> {{---}} время построения множества <tex> X </tex>, <tex> G_X(y) </tex> {{---}} время поиска элемента <tex> x </tex> в множестве <tex> X </tex>, удовлетворяющее решению при заданном <tex> y </tex>, или проверка, что такого <tex> x </tex> не существует. |
}} | }} | ||
| − | '''Meet-in-the-middle''' разбивает задачу пополам и решает всю задачу через частичный расчет половинок. Он работает следующим образом : переберем все возможные значения <tex> {x} </tex> и запишем пару значений <tex> ({x},{f({x})}) </tex> в | + | '''Meet-in-the-middle''' разбивает задачу пополам и решает всю задачу через частичный расчет половинок. Он работает следующим образом: переберем все возможные значения <tex> {x} </tex> и запишем пару значений <tex> ({x},{f({x})}) </tex> в множество. Затем будем перебирать всевозможные значения <tex> y </tex>, для каждого из них будем вычислять <tex> g(y) </tex>, которое мы будем искать в нашем множестве. Если в качестве множества использовать отсортированный массив, а в качестве функции поиска {{---}} [[Целочисленный двоичный поиск | бинарный поиск]], то время работы нашего алгоритма составляет <tex> {O(X\log{X})} </tex> на сортировку, и <tex> {O(Y\log{X})} </tex> на двоичный поиск, что дает в сумме <tex>{O((X + Y)\log{X}})</tex>. |
| − | == Задача о | + | |
| − | Дан массив целых чисел <tex>{A}</tex>. Требуется найти любые | + | == Задача о нахождении четырех чисел с суммой равной нулю == |
| + | Дан массив целых чисел <tex>{A}</tex>. Требуется найти любые <tex> 4 </tex> числа, сумма которых равна <tex> 0 </tex> (одинаковые элементы могут быть использованы несколько раз). | ||
Например : <tex> {A} = ({2,3,1,0,-4,-1}) </tex>. Решением данной задачи является, например, четверка чисел <tex> 3 + 1 + 0 - 4 = 0</tex> или <tex> 0 + 0 + 0 + 0 = 0</tex>. | Например : <tex> {A} = ({2,3,1,0,-4,-1}) </tex>. Решением данной задачи является, например, четверка чисел <tex> 3 + 1 + 0 - 4 = 0</tex> или <tex> 0 + 0 + 0 + 0 = 0</tex>. | ||
| Строка 14: | Строка 15: | ||
=== Реализация === | === Реализация === | ||
| − | // sum | + | <font color=darkgreen>// sum — массив сумм a + b, cnt — счетчик массива sum</font> |
| − | for a = 0 | + | '''function''' findsum('''int['''N''']''' A): String |
| − | + | '''for''' a = 0..N - 1 | |
| − | + | '''for''' b = 0..N - 1 | |
| − | + | sum[cnt].res = A[a] + A[b] | |
| − | + | sum[cnt].a = a | |
| − | + | sum[cnt].b = b | |
| − | + | cnt++ | |
| − | + | sort(sum, key = "res") <font color=darkgreen>// сортируем sum по полю res </font> | |
| − | + | '''for''' c = 0..N - 1 | |
| − | + | '''for''' d = 0..N - 1 | |
| − | + | '''if''' сумма - (A[c] + A[d]) есть в массив sum | |
| − | + | index = индекс суммы -(A[c] + A[d]) | |
| − | + | '''return''' (sum[index].a, sum[index].b, A[c], A[d]) | |
| − | + | '''return''' "No solution" | |
| − | |||
Итоговое время работы <tex> {O(N^2\log{N}}) </tex>. | Итоговое время работы <tex> {O(N^2\log{N}}) </tex>. | ||
| + | Если вместо отсортированного массива использовать [[Хеш-таблица | хэш-таблицу]], то задачу можно будет решить за время <tex> O(N^2) </tex>. | ||
== Задача о рюкзаке == | == Задача о рюкзаке == | ||
| − | Классической задачей является задача о наиболее эффективной упаковке рюкзака. Каждый предмет характеризуется весом (<tex> {w_{i} \ | + | Классической задачей является задача о наиболее эффективной упаковке рюкзака. Каждый предмет характеризуется весом (<tex> {w_{i} \leqslant 10^{9}} </tex> ) и ценностью (<tex>{cost_{i} \leqslant 10^{9}} </tex>). В рюкзак, ограниченный по весу, необходимо набрать вещей с максимальной суммарной стоимостью. Для ее решения изначальное множество вещей N разбивается на два равных(или примерно равных) подмножества, для которых за приемлемое время можно перебрать все варианты и подсчитать суммарный вес и стоимость, а затем для каждого из них найти группу вещей из первого подмножества с максимальной стоимостью, укладывающуюся в ограничение по весу рюкзака. Сложность алгоритма <tex>O({2^{\frac{N}{2}}}\times{N})</tex>. Память <tex> O({2^{\frac{N}{2}}})</tex>. |
| + | |||
| + | === Алгоритм === | ||
| + | Разделим наше множество на две части. Подсчитаем все подмножества из первой части и будем хранить их в массиве <tex>\mathtt{first}</tex>. Отсортируем массив <tex>\mathtt{first}</tex> по весу. Далее пройдемся по этому массиву и оставим только те подмножества, для которых не существует другого подмножества с меньшим весом и большей стоимостью. Очевидно, что подмножества, для которых существует другое, более легкое и одновременно более ценное подмножество, можно удалять. | ||
| + | Таким образом в массиве <tex>\mathtt{first}</tex> мы имеем подмножества, отсортированные не только по весу, но и по стоимости. Тогда начнем перебирать все возможные комбинации вещей из второй половины и находить бинарным поиском удовлетворяющие нам подмножества из первой половины, хранящиеся в массиве <tex>\mathtt{first}</tex>. | ||
=== Реализация === | === Реализация === | ||
| − | + | <font color=darkgreen>// N — количество всех вещей, w[N] — массив весов всех вещей, cost[N] — массив стоимостей всех вещей, R — ограничение по весу рюкзака.</font> | |
| − | + | '''function''' knapsack('''int['''N''']''' w, '''int['''N''']''' cost, '''int''' R): '''int''' | |
| + | sn = N / 2 | ||
| + | fn = N - sn | ||
| + | '''for''' mask = 0..2 ** sn - 1 | ||
| + | '''for''' j = 0..sn | ||
| + | '''if''' j-ый бит mask == 1 | ||
| + | first[i].w += w[j] | ||
| + | first[i].c += cost[j] | ||
| + | sort(first, key = "w") <font color=darkgreen>// сортируем first по весу </font> | ||
| + | '''for''' i = 0..2 ** sn - 1 | ||
| + | '''if''' существует такое подмножество с индексом j, что first[j].w <tex> \leqslant </tex> first[i].w '''and''' first[j].c <tex> \geqslant </tex> first[i].c | ||
| + | удалим множество с индексом i из массива first | ||
| + | '''for''' mask = 0..2 ** fn - 1 | ||
| + | '''for''' j = 0..fn | ||
| + | '''if''' j-ый бит mask == 1 | ||
| + | curw += w[j + sn] | ||
| + | curcost += cost[j + sn] | ||
| + | index = позиция, найденная бинарным поиском в массиве first, подмножества с максимальным весом, не превыщающим R - curv | ||
| + | '''if''' first[index].w <tex> \leqslant </tex> R - curw '''and''' first[index].c + curcost <tex> > </tex> ans | ||
| + | ans = first[index].c + curcost | ||
| + | '''return''' ans | ||
| + | |||
| + | Итоговое время работы <tex> {O({2^{\frac{N}{2}}}\times({N}+\log{2^{\frac{N}{2}}}))} = O({2^{\frac{N}{2}}}\times{N}) </tex>. | ||
| − | + | == Задача о количестве полных подграфов в графе == | |
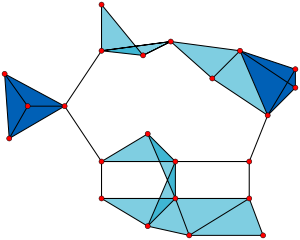
| − | + | [[Файл:cliques.png|450px|thumb|right|Граф с 23 × 1-вершинными кликами (сами вершины), | |
| − | + | 42 × 2-вершинными кликами (отрезки), | |
| − | + | 19 × 3-вершинными кликами (светло-синие и тёмно-синие треугольники) и | |
| − | + | 2 × 4-вершинными кликами (тёмно-синие зоны). Всего 86 клик.]] | |
| − | + | Дан граф <tex>G</tex>, в котором <tex>N</tex> вершин. Требуется подсчитать количество [[Основные_определения_теории_графов#Часто используемые графы | клик]]. | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | Наивное решение — перебор всех возможных подграфов и проверка для каждого, что он является кликой, сложность — <tex>O(2^N \times N^2)</tex> | |
| + | |||
| + | Этот алгоритм можно улучшить до <tex>O(2^N \times N)</tex>. Для этого нужно в функции перебора хранить маску вершин, которые мы ещё можем добавить. Поддерживая эту маску, можно добавлять только «нужные» вершины, и тогда не нужно будет в конце проверять подграф на то что он — клика. Добавлять вершину можно за <tex>O(1)</tex>, используя [[Побитовые_операции#Побитовое И | побитовое И]] текущей маски и строчки матрицы смежности добавляемой вершины. | ||
| + | |||
| + | ===Алгоритм решения=== | ||
| + | Разбиваем граф <tex>G</tex> на <tex>2</tex> графа <tex>{G}_1</tex> и <tex>{G}_2</tex> по <tex>\dfrac{N}{2}</tex> вершин. Находим за <tex>O(2^{\frac{N}{2}})</tex> все клики в каждом из них. | ||
| + | |||
| + | Теперь надо узнать для каждой клики графа <tex>{G}_1</tex> количество клик графа <tex>{G}_2</tex>, таких, что их объединение — клика. Их сумма и есть итоговый ответ. | ||
| + | |||
| + | Для одной клики <tex>K</tex> графа <tex>{G}_1</tex> может быть несколько подходящих клик в <tex>{G}_2</tex>. О клике <tex>K</tex> мы ''"знаем"'' только маску вершин графа <tex>{G}_2</tex>, которые ещё можно добавить. Для каждой такой маски в <tex>{G}_2</tex> нужно предподсчитать ответ. | ||
| + | С помощью динамического программирования предподсчитаем для каждой маски вершин графа <tex>{G}_2</tex> количество клик, вершины которых являются подмножеством выбранной маски. Количество состояний — <tex>2^{\frac{N}{2}}</tex>. Количество переходов:<tex>N</tex> . Асимптотика — <tex>O(2^{\frac{N}{2}} \times N)</tex>. | ||
| + | |||
| + | Для каждой клики <tex>K</tex> (в том числе и пустой) графа <tex>{G}_1</tex> прибавим к глобальному ответу предподсчитанное количество клик, которые можно добавить к <tex>K</tex> (в том числе и пустых). Асимптотика: <tex>O(2^{\frac{N}{2}})</tex>. | ||
| + | |||
| + | Итоговая сложность: <tex>O(2^{\frac{N}{2}} \times N)</tex> | ||
== Задача о нахождении кратчайшего расстояния между двумя вершинами в графе == | == Задача о нахождении кратчайшего расстояния между двумя вершинами в графе == | ||
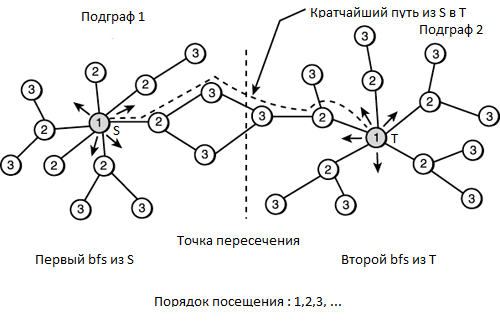
[[Файл:bfs.png|600px|thumb|right|Нахождение кратчайшего расстояния между двумя вершинами]] | [[Файл:bfs.png|600px|thumb|right|Нахождение кратчайшего расстояния между двумя вершинами]] | ||
| − | Еще одна задача, решаемая '''Meet-in-the-middle''' — это нахождение кратчайшего расстояния между двумя вершинами, зная начальное состояние, конечное состояние и то, что длина оптимального пути не превышает | + | Еще одна задача, решаемая '''Meet-in-the-middle''' — это нахождение кратчайшего расстояния между двумя вершинами, зная начальное состояние, конечное состояние и то, что длина оптимального пути не превышает <tex> N </tex>. |
| − | Стандартным подходом для решения данной задачи, является применение алгоритма [[Обход в ширину|обхода в ширину]]. Пусть из каждого состояния у нас есть | + | Стандартным подходом для решения данной задачи, является применение алгоритма [[Обход в ширину|обхода в ширину]]. Пусть из каждого состояния у нас есть <tex> K </tex> переходов, тогда бы мы сгенерировали <tex> {K^{N}} </tex> состояний. Асимптотика данного решения составила бы <tex> {O({K^{N}})} </tex>. '''Meet-in-the-middle''' помогает снизить асимптотику до <tex> {O({K^{\frac{N}{2}}})} </tex>. <br> |
=== Алгоритм решения === | === Алгоритм решения === | ||
| − | 1. Сгенерируем ''' | + | 1. Сгенерируем '''BFS'''-ом все состояния, доступные из начала и конца за <tex> {\dfrac{N}{2}} </tex> или меньше ходов. |
2. Найдем состояния, которые достижимы из начала и из конца. | 2. Найдем состояния, которые достижимы из начала и из конца. | ||
| Строка 80: | Строка 103: | ||
| − | Таким образом, ''' | + | Таким образом, '''BFS-ом''' из двух концов, мы сгенерируем максимум <tex> {O({K^{\frac{N}{2}}})} </tex> состояний. |
== См. также == | == См. также == | ||
| Строка 86: | Строка 109: | ||
* [[Целочисленный двоичный поиск]] | * [[Целочисленный двоичный поиск]] | ||
| − | == | + | ==Источники информации== |
| − | *[http://infoarena.ro/blog/meet-in-the-middle Meet-in-the-middle] | + | *[http://infoarena.ro/blog/meet-in-the-middle infoarena.ro — Meet-in-the-middle] |
| − | *[http://g6prog.narod.ru/dpl.ps Лекции по информатике(36 страница)] | + | *[http://g6prog.narod.ru/dpl.ps g6prog.narod.ru — Лекции по информатике (36 страница)] |
| + | *[https://en.wikipedia.org/wiki/Clique_(graph_theory) wikipedia.org — Clique] | ||
[[Категория: Дискретная математика и алгоритмы]] | [[Категория: Дискретная математика и алгоритмы]] | ||
[[Категория: Динамическое программирование ]] | [[Категория: Динамическое программирование ]] | ||
| + | |||
| + | [[Категория: Классические задачи динамического программирования ]] | ||
Текущая версия на 19:31, 4 сентября 2022
| Определение: |
| Встреча в середине (англ. Meet-in-the-middle) — это метод решения уравнения вида , где и , который работает за время , где — время построения множества , — время поиска элемента в множестве , удовлетворяющее решению при заданном , или проверка, что такого не существует. |
Meet-in-the-middle разбивает задачу пополам и решает всю задачу через частичный расчет половинок. Он работает следующим образом: переберем все возможные значения и запишем пару значений в множество. Затем будем перебирать всевозможные значения , для каждого из них будем вычислять , которое мы будем искать в нашем множестве. Если в качестве множества использовать отсортированный массив, а в качестве функции поиска — бинарный поиск, то время работы нашего алгоритма составляет на сортировку, и на двоичный поиск, что дает в сумме .
Содержание
Задача о нахождении четырех чисел с суммой равной нулю
Дан массив целых чисел . Требуется найти любые числа, сумма которых равна (одинаковые элементы могут быть использованы несколько раз).
Например : . Решением данной задачи является, например, четверка чисел или .
Наивный алгоритм заключается в переборе всевозможных комбинаций чисел. Это решение работает за . Теперь, с помощью Meet-in-the-middle мы можем сократить время работы до .
Для этого заметим, что сумму можно записать как . Мы будем хранить все пар сумм в массиве , который мы отсортируем. Далее перебираем все пар сумм и проверяем бинарным поиском, есть ли сумма в массиве .
Реализация
// sum — массив сумм a + b, cnt — счетчик массива sum
function findsum(int[N] A): String
for a = 0..N - 1
for b = 0..N - 1
sum[cnt].res = A[a] + A[b]
sum[cnt].a = a
sum[cnt].b = b
cnt++
sort(sum, key = "res") // сортируем sum по полю res
for c = 0..N - 1
for d = 0..N - 1
if сумма - (A[c] + A[d]) есть в массив sum
index = индекс суммы -(A[c] + A[d])
return (sum[index].a, sum[index].b, A[c], A[d])
return "No solution"
Итоговое время работы .
Если вместо отсортированного массива использовать хэш-таблицу, то задачу можно будет решить за время .
Задача о рюкзаке
Классической задачей является задача о наиболее эффективной упаковке рюкзака. Каждый предмет характеризуется весом ( ) и ценностью (). В рюкзак, ограниченный по весу, необходимо набрать вещей с максимальной суммарной стоимостью. Для ее решения изначальное множество вещей N разбивается на два равных(или примерно равных) подмножества, для которых за приемлемое время можно перебрать все варианты и подсчитать суммарный вес и стоимость, а затем для каждого из них найти группу вещей из первого подмножества с максимальной стоимостью, укладывающуюся в ограничение по весу рюкзака. Сложность алгоритма . Память .
Алгоритм
Разделим наше множество на две части. Подсчитаем все подмножества из первой части и будем хранить их в массиве . Отсортируем массив по весу. Далее пройдемся по этому массиву и оставим только те подмножества, для которых не существует другого подмножества с меньшим весом и большей стоимостью. Очевидно, что подмножества, для которых существует другое, более легкое и одновременно более ценное подмножество, можно удалять. Таким образом в массиве мы имеем подмножества, отсортированные не только по весу, но и по стоимости. Тогда начнем перебирать все возможные комбинации вещей из второй половины и находить бинарным поиском удовлетворяющие нам подмножества из первой половины, хранящиеся в массиве .
Реализация
// N — количество всех вещей, w[N] — массив весов всех вещей, cost[N] — массив стоимостей всех вещей, R — ограничение по весу рюкзака.
function knapsack(int[N] w, int[N] cost, int R): int
sn = N / 2
fn = N - sn
for mask = 0..2 ** sn - 1
for j = 0..sn
if j-ый бит mask == 1
first[i].w += w[j]
first[i].c += cost[j]
sort(first, key = "w") // сортируем first по весу
for i = 0..2 ** sn - 1
if существует такое подмножество с индексом j, что first[j].w first[i].w and first[j].c first[i].c
удалим множество с индексом i из массива first
for mask = 0..2 ** fn - 1
for j = 0..fn
if j-ый бит mask == 1
curw += w[j + sn]
curcost += cost[j + sn]
index = позиция, найденная бинарным поиском в массиве first, подмножества с максимальным весом, не превыщающим R - curv
if first[index].w R - curw and first[index].c + curcost ans
ans = first[index].c + curcost
return ans
Итоговое время работы .
Задача о количестве полных подграфов в графе
Дан граф , в котором вершин. Требуется подсчитать количество клик.
Наивное решение — перебор всех возможных подграфов и проверка для каждого, что он является кликой, сложность —
Этот алгоритм можно улучшить до . Для этого нужно в функции перебора хранить маску вершин, которые мы ещё можем добавить. Поддерживая эту маску, можно добавлять только «нужные» вершины, и тогда не нужно будет в конце проверять подграф на то что он — клика. Добавлять вершину можно за , используя побитовое И текущей маски и строчки матрицы смежности добавляемой вершины.
Алгоритм решения
Разбиваем граф на графа и по вершин. Находим за все клики в каждом из них.
Теперь надо узнать для каждой клики графа количество клик графа , таких, что их объединение — клика. Их сумма и есть итоговый ответ.
Для одной клики графа может быть несколько подходящих клик в . О клике мы "знаем" только маску вершин графа , которые ещё можно добавить. Для каждой такой маски в нужно предподсчитать ответ. С помощью динамического программирования предподсчитаем для каждой маски вершин графа количество клик, вершины которых являются подмножеством выбранной маски. Количество состояний — . Количество переходов: . Асимптотика — .
Для каждой клики (в том числе и пустой) графа прибавим к глобальному ответу предподсчитанное количество клик, которые можно добавить к (в том числе и пустых). Асимптотика: .
Итоговая сложность:
Задача о нахождении кратчайшего расстояния между двумя вершинами в графе
Еще одна задача, решаемая Meet-in-the-middle — это нахождение кратчайшего расстояния между двумя вершинами, зная начальное состояние, конечное состояние и то, что длина оптимального пути не превышает .
Стандартным подходом для решения данной задачи, является применение алгоритма обхода в ширину. Пусть из каждого состояния у нас есть переходов, тогда бы мы сгенерировали состояний. Асимптотика данного решения составила бы . Meet-in-the-middle помогает снизить асимптотику до .
Алгоритм решения
1. Сгенерируем BFS-ом все состояния, доступные из начала и конца за или меньше ходов.
2. Найдем состояния, которые достижимы из начала и из конца.
3. Найдем среди них наилучшее по сумме длин путей.
Таким образом, BFS-ом из двух концов, мы сгенерируем максимум состояний.