Задача о наибольшей подпоследовательности-палиндроме — различия между версиями
(→Псевдокод) |
м (rollbackEdits.php mass rollback) |
||
| (не показано 38 промежуточных версий 6 участников) | |||
| Строка 1: | Строка 1: | ||
| − | + | {{Определение|definition='''Палиндромом''' (англ. <i>Palindrome</i>) называется строка, которая одинаково читается как слева направо, так и справа налево.}} | |
| + | {{Определение|definition='''Подпоследовательностью-палиндромом данной строки''' (англ. <i>Largest Palindromic Subsequence</i>) называется последовательность символов из данной строки, не обязательно идущих подряд, являющаяся палиндромом. }} | ||
| + | Например, '''''HELOLEH''''' является подпоследовательностью-палиндромом строки '''''HTEOLFEOLEH'''''. | ||
| − | = | + | {{Задача |
| + | |definition = | ||
| + | Задача о '''наибольшей подпоследовательности-палиндроме''' {{---}} это задача о поиске наибольшей подпоследовательности, которую можно получить вычеркиванием некоторых букв из данной последовательности таким образом, что оставшаяся подпоследовательность будет палиндромом. | ||
| + | }} | ||
| − | {{ | + | == Решение == |
| + | Обозначим данную последовательность через <tex>S</tex>, а ее элементы {{---}} через <tex>S[i], 0 \leqslant i \leqslant n - 1</tex>, где <tex>n</tex> {{---}} длина строки <tex>S</tex>. Будем рассматривать возможные подпоследовательности данной последовательности с <tex>i - </tex>го по <tex>j - </tex>ый символ включительно, обозначив её как <tex>S(i, j)</tex>. Длины максимальных подпалиндромов для данной последовательности будем записывать в двумерный массив <tex>L</tex>: <tex>L[i][j]</tex> {{---}} длина максимальной подпоследовательности-палиндрома, который можно получить из последовательности <tex>S(i, j)</tex>. | ||
| − | {{ | + | Начнем решать задачу с простых подпоследовательностей. Для последовательности из одного элемента (то есть подпоследовательности вида <tex>S(i, i)</tex>) ответ очевиден {{---}} ничего вычеркивать не надо, такая строка будет искомой подпоследовательностью-палиндромом. Для последовательности из двух элементов <tex>S(i, i + 1)</tex> возможны два варианта: если элементы равны, то мы имеем подпоследовательность-палиндром, ничего вычеркивать не надо. Если же элементы не равны, то вычеркиваем любой. |
| − | + | Пусть теперь нам дана подпоследовательность <tex>S(i, j)</tex>. Если <tex>S[i]</tex> и <tex>S[j]</tex> элементы подпоследовательности не совпадают, то один из них нужно вычеркнуть. Тогда у нас останется подпоследовательность <tex>S(i, j - 1)</tex> или <tex>S(i + 1, j)</tex> {{---}} то есть мы сведем задачу к подзадаче: <tex>L[i][j] = \max(L[i][j - 1], L[i + 1][j])</tex>. Если же первый и последний элементы равны, то мы можем оставить оба, но необходимо знать решение задачи <tex>S(i + 1, j - 1):L[i][j] = L[i + 1][j - 1] + 2</tex>. Таким образом получаем следующее рекуррентное соотношение: | |
| − | + | ||
| − | + | <tex> | |
| − | + | L[i][j] = | |
| − | + | \begin{cases} | |
| + | 1, & i = j\\ | ||
| + | 0, & i > j\\ | ||
| + | L[i + 1][j - 1] + 2, & s[i] = s[j] \\ | ||
| + | \max(L[i][j - 1], L[i + 1][j]), & s[i] \neq s[j] | ||
| + | \end{cases} | ||
| + | </tex> | ||
| − | |||
| − | |||
| − | |||
=== Асимптотика === | === Асимптотика === | ||
| − | Каждый элемент массива мы вычисляем 1 раз за <tex>O(1)</tex> обращаясь к уже вычисленным элементам. Так как размер массива <tex>n \times n</tex>, то алгоритм работает за <tex>O(n^2)</tex> | + | Каждый элемент массива мы вычисляем <tex>1</tex> раз за <tex>O(1)</tex> обращаясь к уже вычисленным элементам. Так как размер массива <tex>n \times n</tex>, то алгоритм работает за <tex>O(n^2)</tex> |
== Пример == | == Пример == | ||
| − | Рассмотрим решение на примере последовательности '''''ABACCBA'''''. Первым делом заполняем диагональ массива единицами, они будут соответствовать подпоследовательностями <tex>S(i, i)</tex> из одного элемента. Затем начинаем рассматривать подпоследовательности длины два. Во всех подпоследовательностях, кроме <tex>S(4 | + | Рассмотрим решение на примере последовательности '''''ABACCBA'''''. Первым делом заполняем диагональ массива единицами, они будут соответствовать подпоследовательностями <tex>S(i, i)</tex> из одного элемента. Затем начинаем рассматривать подпоследовательности длины два. Во всех подпоследовательностях, кроме <tex>S(3, 4)</tex>, элементы различны, поэтому в соответствующие ячейки запишем <tex>1</tex>, а в <tex>L[3][4]</tex> {{---}} <tex>2</tex>. |
| + | |||
| + | Получается, что мы будем заполнять массив по диагоналям, начиная с главной диагонали. Для подпоследовательностей длины <tex>3</tex> получаются следующие значения: в подпоследовательности '''''ABA''''' первый и последний элемент равны, поэтому <tex>L[0][2] = L[1][1] + 2</tex>. В остальных подпоследовательностях первый и последний элементы различны. | ||
| − | |||
| − | '''''BAC''''': <tex>L[ | + | '''''BAC''''': <tex>L[1][3] = \max(L[1][2], L[2][3]) = 1</tex> |
| − | '''''ACC''''': <tex>L[ | + | '''''ACC''''': <tex>L[2][4] = \max(L[2][3], L[3][4]) = 2</tex> |
| − | '''''CCB''''': <tex>L[ | + | '''''CCB''''': <tex>L[3][5] = \max(L[3][4], L[4][5]) = 2</tex> |
| − | '''''CBA''''': <tex>L[ | + | '''''CBA''''': <tex>L[4][6] = \max(L[4][5], L[5][6]) = 1</tex> |
| − | Продолжая далее аналогичные рассуждения, заполним все ячейки | + | Продолжая далее аналогичные рассуждения, заполним все ячейки над диагональю и в ячейке <tex>L[0][6]</tex> получим ответ {{---}} <tex>6</tex>. |
| − | Если же в задаче необходимо вывести не длину, а саму подпоследовательность-палиндром, то дополнительно к массиву длин мы должны построить массив переходов | + | Если же в задаче необходимо вывести не длину, а саму подпоследовательность-палиндром, то дополнительно к массиву длин мы должны построить массив переходов {{---}} для каждой ячейки запомнить, какой из случаев был реализован. |
| + | |||
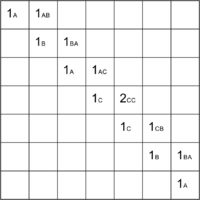
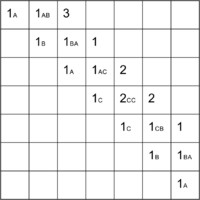
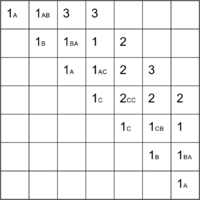
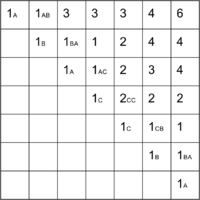
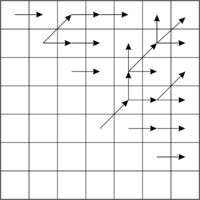
| + | Последовательность заполнения массива и массив переходов см. на изображениях ниже. | ||
| + | |||
| + | [[Файл:Palindrome11.png|200px|Заполнение массива длин (1)]] | ||
| + | [[Файл:Palindrome12.png|200px|Заполнение массива длин (2)]] | ||
| + | [[Файл:Palindrome13.png|200px|Заполнение массива длин (3)]] | ||
| + | [[Файл:Palindrome14.png|200px|Заполнение массива длин (4)]] | ||
| + | [[Файл:Palindrome15.png|200px|Массив переходов]] | ||
== Псевдокод == | == Псевдокод == | ||
Перед вызовом процедуры заполняем <tex>L[][]</tex> начальными значениями: <tex>L[i][j] = 1</tex> если <tex>i=j</tex>, <tex>L[i][j] = 0</tex>, если <tex>i>j</tex>, в остальных случаях <tex>L[i][j]=-1</tex>. | Перед вызовом процедуры заполняем <tex>L[][]</tex> начальными значениями: <tex>L[i][j] = 1</tex> если <tex>i=j</tex>, <tex>L[i][j] = 0</tex>, если <tex>i>j</tex>, в остальных случаях <tex>L[i][j]=-1</tex>. | ||
| − | При | + | При первом вызове функции в качестве аргументов передаем индексы первого и последнего элементов исходной строки. Например для строки длиной <tex> N </tex> вызов функции будет иметь следующий вид: <tex> \mathrm{palSubSeq(0, N - 1)}</tex>. Искомая же длина будет записана в ячейке <tex>L[0][N-1]</tex>. |
| − | <code> | + | |
| − | ''' | + | '''Функция для вычисления длины палиндрома''': |
| − | '''if''' L[ | + | *Границы исходной последовательности: <tex> \mathtt{left, right}</tex> |
| − | + | <code style = "display: inline-block;"> | |
| − | + | '''int''' palSubSeq(left: '''int''', right: '''int'''): | |
| − | + | '''if''' L[left][right] == -1 | |
| − | + | '''if''' s[left] == s[right] | |
| − | '''if''' | + | L[left][right] = palSubSeq(left + 1, right - 1) + 2 |
| − | + | '''else''' | |
| + | L[left][right] = max(palSubSeq(left + 1, right), palSubSeq(left, right - 1)) | ||
| + | '''return''' L[left][right] | ||
| + | </code> | ||
| + | '''Процедура для построения искомого палиндрома''': | ||
| + | *Границы исходной последовательности: <tex> \mathtt{left, right}</tex> | ||
| + | *Границы искомой подпоследовательности-палиндрома, где правой границей будет длина найденного палиндрома: <tex> \mathtt{palLeft, palRight}</tex> | ||
| + | <code style = "display: inline-block;"> | ||
| + | <font color=green>// palindrome {{---}} массив символов, где в palindrome[i] содержится символ искомой последовательности-палиндрома</font> | ||
| + | palChars(left: '''int''', right: '''int''', palLeft: '''int''', palRight: '''int'''): | ||
| + | '''while''' left <tex>\leqslant </tex> right | ||
| + | '''if''' left == right '''and''' L[left][right] == 1 | ||
| + | palindrome[palLeft++] = S[left++] | ||
'''else''' | '''else''' | ||
| − | + | '''if''' S[left] == S[right] | |
| − | + | palindrome[palLeft++] = S[left++] | |
| − | + | palindrome[palRight--] = S[right--] | |
| − | + | '''else''' | |
| − | + | '''if''' L[left + 1][right] <tex> > </tex> L[left][right - 1] | |
| − | + | left++ | |
| + | '''else''' | ||
| + | right-- | ||
</code> | </code> | ||
| − | |||
| − | |||
| − | |||
| − | |||
== См. также == | == См. также == | ||
* [[Задача о наибольшей общей подпоследовательности]] | * [[Задача о наибольшей общей подпоследовательности]] | ||
* [[Задача о наибольшей возрастающей подпоследовательности]] | * [[Задача о наибольшей возрастающей подпоследовательности]] | ||
| + | * [[Задача о наибольшей общей палиндромной подпоследовательности]] | ||
| + | |||
| + | ==Источники информации== | ||
| + | * [[wikipedia:ru:Палиндром|Википедия {{---}} Палиндром]] | ||
| + | * [[wikipedia:Palindrome|Wikipedia {{---}} Palindrome]] | ||
| + | * [http://wcipeg.com/wiki/Longest_palindromic_subsequence Wikipedia {{---}} Longest palindromic subsequence] | ||
[[Категория:Дискретная математика и алгоритмы]] | [[Категория:Дискретная математика и алгоритмы]] | ||
[[Категория:Динамическое программирование]] | [[Категория:Динамическое программирование]] | ||
Текущая версия на 19:42, 4 сентября 2022
| Определение: |
| Палиндромом (англ. Palindrome) называется строка, которая одинаково читается как слева направо, так и справа налево. |
| Определение: |
| Подпоследовательностью-палиндромом данной строки (англ. Largest Palindromic Subsequence) называется последовательность символов из данной строки, не обязательно идущих подряд, являющаяся палиндромом. |
Например, HELOLEH является подпоследовательностью-палиндромом строки HTEOLFEOLEH.
| Задача: |
| Задача о наибольшей подпоследовательности-палиндроме — это задача о поиске наибольшей подпоследовательности, которую можно получить вычеркиванием некоторых букв из данной последовательности таким образом, что оставшаяся подпоследовательность будет палиндромом. |
Решение
Обозначим данную последовательность через , а ее элементы — через , где — длина строки . Будем рассматривать возможные подпоследовательности данной последовательности с го по ый символ включительно, обозначив её как . Длины максимальных подпалиндромов для данной последовательности будем записывать в двумерный массив : — длина максимальной подпоследовательности-палиндрома, который можно получить из последовательности .
Начнем решать задачу с простых подпоследовательностей. Для последовательности из одного элемента (то есть подпоследовательности вида ) ответ очевиден — ничего вычеркивать не надо, такая строка будет искомой подпоследовательностью-палиндромом. Для последовательности из двух элементов возможны два варианта: если элементы равны, то мы имеем подпоследовательность-палиндром, ничего вычеркивать не надо. Если же элементы не равны, то вычеркиваем любой.
Пусть теперь нам дана подпоследовательность . Если и элементы подпоследовательности не совпадают, то один из них нужно вычеркнуть. Тогда у нас останется подпоследовательность или — то есть мы сведем задачу к подзадаче: . Если же первый и последний элементы равны, то мы можем оставить оба, но необходимо знать решение задачи . Таким образом получаем следующее рекуррентное соотношение:
Асимптотика
Каждый элемент массива мы вычисляем раз за обращаясь к уже вычисленным элементам. Так как размер массива , то алгоритм работает за
Пример
Рассмотрим решение на примере последовательности ABACCBA. Первым делом заполняем диагональ массива единицами, они будут соответствовать подпоследовательностями из одного элемента. Затем начинаем рассматривать подпоследовательности длины два. Во всех подпоследовательностях, кроме , элементы различны, поэтому в соответствующие ячейки запишем , а в — .
Получается, что мы будем заполнять массив по диагоналям, начиная с главной диагонали. Для подпоследовательностей длины получаются следующие значения: в подпоследовательности ABA первый и последний элемент равны, поэтому . В остальных подпоследовательностях первый и последний элементы различны.
BAC:
ACC:
CCB:
CBA:
Продолжая далее аналогичные рассуждения, заполним все ячейки над диагональю и в ячейке получим ответ — .
Если же в задаче необходимо вывести не длину, а саму подпоследовательность-палиндром, то дополнительно к массиву длин мы должны построить массив переходов — для каждой ячейки запомнить, какой из случаев был реализован.
Последовательность заполнения массива и массив переходов см. на изображениях ниже.
Псевдокод
Перед вызовом процедуры заполняем начальными значениями: если , , если , в остальных случаях . При первом вызове функции в качестве аргументов передаем индексы первого и последнего элементов исходной строки. Например для строки длиной вызов функции будет иметь следующий вид: . Искомая же длина будет записана в ячейке .
Функция для вычисления длины палиндрома:
- Границы исходной последовательности:
int palSubSeq(left: int, right: int):
if L[left][right] == -1
if s[left] == s[right]
L[left][right] = palSubSeq(left + 1, right - 1) + 2
else
L[left][right] = max(palSubSeq(left + 1, right), palSubSeq(left, right - 1))
return L[left][right]
Процедура для построения искомого палиндрома:
- Границы исходной последовательности:
- Границы искомой подпоследовательности-палиндрома, где правой границей будет длина найденного палиндрома:
// palindrome — массив символов, где в palindrome[i] содержится символ искомой последовательности-палиндрома palChars(left: int, right: int, palLeft: int, palRight: int): while left right if left == right and L[left][right] == 1 palindrome[palLeft++] = S[left++] else if S[left] == S[right] palindrome[palLeft++] = S[left++] palindrome[palRight--] = S[right--] else if L[left + 1][right] L[left][right - 1] left++ else right--
См. также
- Задача о наибольшей общей подпоследовательности
- Задача о наибольшей возрастающей подпоследовательности
- Задача о наибольшей общей палиндромной подпоследовательности