Задача об ожерельях — различия между версиями
Korektur (обсуждение | вклад) (Новая страница: «{{Определение |definition= Требуется посчитать количество ожерелий из <tex>n</tex> бусинок, каждая ...») |
м (rollbackEdits.php mass rollback) |
||
| (не показано 57 промежуточных версий 15 участников) | |||
| Строка 1: | Строка 1: | ||
| − | {{ | + | {{Задача |
|definition= | |definition= | ||
Требуется посчитать количество ожерелий из <tex>n</tex> бусинок, каждая из которых может быть покрашена в один из <tex> k </tex> цветов. При сравнении двух ожерелий их можно поворачивать, но не переворачивать (т.е. разрешается сделать циклический сдвиг).}} | Требуется посчитать количество ожерелий из <tex>n</tex> бусинок, каждая из которых может быть покрашена в один из <tex> k </tex> цветов. При сравнении двух ожерелий их можно поворачивать, но не переворачивать (т.е. разрешается сделать циклический сдвиг).}} | ||
| − | Решение этой задачи опирается на лемму | + | Решение этой задачи опирается на [[Лемма Бёрнсайда и Теорема Пойа|лемму Бёрнсайда и теорему Пойа]]. |
| − | {{ | + | == Алгоритм решения задачи про ожерелья == |
| − | + | ||
| − | + | Пусть нам даны бусинки <tex>k</tex> различных цветов, а ожерелье должно состоять из <tex>n</tex> бусинок. | |
| − | }} | + | |
| − | + | Для решения воспользуемся формулой из теоремы Пойа. | |
| + | |||
| + | |||
| + | <tex>|C| =</tex> <tex> \dfrac{1} {|G|}</tex><tex>\sum\limits_{l \in G} k^{P(l)}</tex> | ||
| + | |||
| + | По условию, перестановкой инвариантной данной будет любая перестановка, полученная из данной циклическим сдвигом. | ||
| + | Очевидно, что для каждой перестановки длины <tex>n</tex> существует ровно <tex>n - 1</tex> инвариантная перестановка, то есть всего инвариантных перестановок в каждом классе <tex>n</tex>, теперь найдем <tex>P(i)</tex>. Заметим, что в <tex>i</tex>-ой перестановке на <tex>l</tex>-ой позиции стоит элемент <tex>(i + l)\bmod n</tex>. Также, заметим, что элемент <tex>a</tex> переходит в элемент <tex>a + in</tex>, где <tex>i = 1, 2, \ldots k</tex>. Из этого следует, что длина цикла для <tex>i</tex>-ой перестановки равна <tex> \dfrac{\mathrm{lcm}(n, i)}{i} = \dfrac{n}{\mathrm{gcd}(i,n)}</tex>, где <tex>\mathrm{gcd}(i, n)</tex> {{---}} [[Наибольший общий делитель|НОД<tex>(i, n)</tex>]], <tex>\mathrm{lcm}(i, n)</tex> {{---}} [[Наименьшее общее кратное|НОК<tex>(i, n)</tex>]]. Откуда следует что: | ||
| + | |||
| + | <tex>|C| =</tex> <tex> \dfrac{1} {n}</tex><tex>\sum\limits_{i = 1}^{n} k^{\mathrm{gcd}(i,n)}</tex>. | ||
| + | |||
| + | |||
| + | где <tex>|C|</tex> {{---}} кол-во различных ожерелий,которые можно составить из <tex>n</tex> бусинок <tex>k</tex> различных цветов. | ||
| + | |||
| − | {{ | + | Если раскраски ожерелья одинаковые, то они принадлежат одной [[Орбита|орбите]], т.е. одна получается из другой некоторым преобразованием симметрии. Неподвижные точки поворота есть только у тождественного поворота и их <tex>n</tex> штук. Тогда, по [[Лемма Бёрнсайда и Теорема Пойа|лемме Бёрнсайда]], число орбит равняется <tex>\dfrac{n}{p}=\operatorname{gcd}(n,i)</tex>, где <tex>p</tex> минимальное число такое, что <tex>ip</tex> делится на <tex>n</tex>, и число их раскрасок <tex>N_i=k^{\operatorname{gcd}(n,i)}</tex>. Сумма же инвариантных раскрасок для всех поворотов: <tex>S=\sum\limits_{i=1}^{n}N_i=\sum\limits_{i=1}^{n}k^{\operatorname{gcd}(n,i)}</tex>. В последней сумме <tex>\varphi(n)</tex> слагаемых <tex>(\varphi(n)</tex> {{---}} [[Функция Эйлера|функция Эйлера]]<tex>)</tex>, для которых <tex>\operatorname{gcd}(n,i)=1</tex>. Если же <tex>\operatorname{gcd}(n,i)=q</tex>, то <tex>\operatorname{gcd}\left(\dfrac{n}{q},\dfrac{i}{q}\right)=1</tex>. Чтобы определить количество таких <tex>i</tex>, меньших <tex>n</tex>, нужно перебрать числа вида <tex>i=lq,\,0\leqslant l\leqslant \dfrac{n}{q}</tex> и проверять их на условие <tex>1=\operatorname{gcd}\left(\dfrac{n}{q},\dfrac{i}{q}\right)=\operatorname{gcd}\left(\dfrac{n}{q},l\right)</tex>. Таких чисел, очевидно, <tex>\varphi\left(\dfrac{n}{q}\right)</tex> (по определению <tex>\varphi(n)</tex>). Поэтому сумму можно заменить: <tex>S=\sum\limits_{i=1}^{n}k^{\operatorname{gcd}(n,i)}=\sum\limits_{q|n}\varphi\left(\dfrac{n}{q}\right)k^q</tex>. |
| − | | | ||
| − | |||
| − | }} | ||
| − | == | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | <tex> C = | + | Тогда <tex>|C| =</tex> <tex> \dfrac{1} {n}</tex><tex>\sum\limits_{q|n}\varphi\left(\dfrac{n}{q}\right)k^q</tex>. |
| − | |||
| − | |||
| − | <tex>\sum\limits_{ | ||
| + | == Алгоритм решения задачи про ожерелья с отражениями== | ||
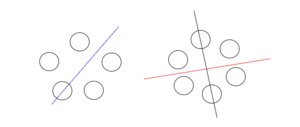
| − | < | + | [[Файл:axis_of_braclets.png|300px|thumb|right|Слева пример оси для нечётного случая. Справа для чётного.]] |
| + | Пусть теперь ожерелья считаются одинаковыми, если они не только переходят друг в друга поворотом, но и отражением относительно некоторой оси (ось может проходить через две противоположные бусинки или через две противоположные пустоты в чётном случае и через бусинку и пустоту напротив неё в нечётном случае). Такие ожерелья называются bracelets <ref>[https://en.wikipedia.org/wiki/Necklace_(combinatorics) Necklace (combinatorics)]</ref>. | ||
| + | Будем пользоваться [[Лемма Бёрнсайда и Теорема Пойа|леммой Бёрнсайда]]. | ||
| + | Разберём два случая. | ||
| + | Для начала покажем, что в качестве операций требуется рассматривать только повороты и отражения. | ||
| + | * Поворот и отражение {{---}} отражение. | ||
| + | Занумеруем наши бусинки по часовой стрелке. Поворот и отражение не меняют порядка (в каком-то направлении бусинки занумерованы по порядку). Нетрудно понять, что отражение меняет направление обхода наших бусинок и не меняет порядка. Если мы сначала сделаем поворот, а потом отразим относительно какой-нибудь оси, то мы то самое же можем получить и обыкновенным отражением относительно какой-то оси. Такая ось найдётся, потому что всегда можно выбрать ось, что поставит первую бусинку на своё изначальное место, поменяв направление обхода (если перебирать все оси подряд, начиная с оси, проходящей через нужную нам бусинку, то изначально она останется на своём месте, потом сместится на одно место, потом на два и.т.д.). Поэтому поворот и отражение не добавляет нам новой операции. | ||
| − | + | * Отражение и поворот {{---}} отражение. | |
| + | Аналогичные рассуждения. | ||
| + | * Отражение и отражение {{---}} поворот. | ||
| + | Тут мы дважды меняем направление обхода, но не меняем порядка. Поэтому данная операция заменяется обычным поворотом. | ||
| − | + | Пусть число бусинок нечётное, тогда мы имеем <tex>n</tex> осей, проходящих через каждую бусинку. Рассмотрим одну ось. Возьмём половину бусинок с одной стороны от оси и ту бусинку, через которую проходит данная ось. Мы можем окрасить их в произвольные цвета, а остальная половина по ним однозначно восстановится. Таким образом количество неподвижных точек для одной оси будет <tex>k^{\frac{n + 1}{2}}</tex>. | |
| + | Операций в группе будет в два раза больше, чем было: <tex>2n</tex> (<tex>n</tex> сдвигов и <tex>n</tex> отражений). | ||
| − | + | По Лемме Бёрнсайда: | |
| + | <tex> |B| = </tex> <tex>\dfrac{1} {|G|}</tex><tex>\sum\limits_{k \in G}I(k)</tex> | ||
| − | + | <tex> |G| = 2n</tex>. Первые <tex>n</tex> операций {{---}} повороты, и сумма количества их неподвижных точек, делённая на <tex>2n</tex>, принимает значение <tex>\dfrac{|C|} {2}</tex>, где <tex>|C|</tex> - количество ожерелий из <tex>n</tex> бусинок <tex>k</tex> различных цветов без отражений (задача выше) т.к. деление в задаче без отражений происходило на <tex>n</tex>, а здесь на <tex>2n</tex>. Следующие <tex>n</tex> операций {{---}} отражения. У каждой такой операции <tex>k^{\frac{n + 1}{2}}</tex> неподвижных точек. Поэтому сумма получается <tex>k^{\frac{n + 1}{2}}n</tex>. | |
| − | <tex>C | + | <tex>|B| = \dfrac{|C|}{2} + \dfrac{1}{2n}k^{\dfrac{n + 1}{2}}n = \dfrac{|C|}{2} + \dfrac{1}{2}k^{\dfrac{n + 1}{2}} </tex><tex> = \dfrac{1} {2n}\sum\limits_{q|n}\varphi\left(\dfrac{n}{q}\right)k^q + \dfrac{1}{2}k^{\dfrac{n + 1}{2}} </tex> |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| + | Разберём теперь чётный случай. | ||
| + | Тут мы имеем <tex>\frac{n}{2}</tex> осей, проходящих через пустоты между бусинками (ось можно провести через пустоту после каждой бусинки, но половина из них будет повторяться). В таких вот случаях можно выбрать по <tex>\frac{n}{2}</tex> бусинок и дать им произвольные цвета. Остальная половина восстановится по ним. Таким образом для данных осей количество неподвижных точек будет <tex>k^{\frac{n}{2}}</tex>. | ||
| + | Ещё у нас есть <tex>\frac{n}{2}</tex> осей, проходящих через бусинки. В данных случаях мы можем выбрать по <tex>\frac{n}{2} + 1</tex> бусинок (бусинки на оси и все по одну какую-то сторону от неё). То есть будет <tex>k^{\frac{n}{2} + 1}</tex> неподвижных точек. Операций также <tex>2n</tex>. | ||
| − | + | По Лемме Бёрнсайда: | |
| − | |||
| − | |||
| − | == | + | <tex>|B| = \dfrac{|C|}{2} + \dfrac{1}{2n}\left(\dfrac{n}{2}k^{\frac{n}{2}} + \dfrac{n}{2}k^{\frac{n}{2} + 1}\right)</tex> <tex>= \dfrac{|C|}{2} + \dfrac{1}{4}k^{\frac{n}{2}}(k + 1) = \dfrac{1} {2n}\sum\limits_{q|n}\varphi\left(\dfrac{n}{q}\right)k^q + \dfrac{1}{4}k^{\frac{n}{2}}(k+1)</tex> |
| − | + | == См. также == | |
| + | * [[Лемма Бёрнсайда и Теорема Пойа]] | ||
| + | * [[Функция Эйлера]] | ||
| − | + | == Примечания == | |
| + | <references/> | ||
| + | == Источники информации == | ||
| + | * [https://ru.wikipedia.org/wiki/%D0%A2%D0%B5%D0%BE%D1%80%D0%B5%D0%BC%D0%B0_%D0%A0%D0%B5%D0%B4%D1%84%D0%B8%D0%BB%D0%B4%D0%B0_%E2%80%94_%D0%9F%D0%BE%D0%B9%D0%B0#.D0.97.D0.B0.D0.B4.D0.B0.D1.87.D0.B0_.D0.BE_.D0.BA.D0.BE.D0.BB.D0.B8.D1.87.D0.B5.D1.81.D1.82.D0.B2.D0.B5_.D0.BE.D0.B6.D0.B5.D1.80.D0.B5.D0.BB.D0.B8.D0.B9 Википедия {{---}} Теорема Редфилда — Пойа, Задача о количестве ожерелий] | ||
| + | * [http://e-maxx.ru/algo/necklace_colouring MAXimal::algo::Ожерелья] | ||
| − | |||
| − | + | [[Категория: Дискретная математика и алгоритмы]] | |
| + | [[Категория: Комбинаторика]] | ||
| + | [[Категория: Теория групп]] | ||
Текущая версия на 19:42, 4 сентября 2022
| Задача: |
| Требуется посчитать количество ожерелий из бусинок, каждая из которых может быть покрашена в один из цветов. При сравнении двух ожерелий их можно поворачивать, но не переворачивать (т.е. разрешается сделать циклический сдвиг). |
Решение этой задачи опирается на лемму Бёрнсайда и теорему Пойа.
Алгоритм решения задачи про ожерелья
Пусть нам даны бусинки различных цветов, а ожерелье должно состоять из бусинок.
Для решения воспользуемся формулой из теоремы Пойа.
По условию, перестановкой инвариантной данной будет любая перестановка, полученная из данной циклическим сдвигом. Очевидно, что для каждой перестановки длины существует ровно инвариантная перестановка, то есть всего инвариантных перестановок в каждом классе , теперь найдем . Заметим, что в -ой перестановке на -ой позиции стоит элемент . Также, заметим, что элемент переходит в элемент , где . Из этого следует, что длина цикла для -ой перестановки равна , где — НОД, — НОК. Откуда следует что:
.
где — кол-во различных ожерелий,которые можно составить из бусинок различных цветов.
Если раскраски ожерелья одинаковые, то они принадлежат одной орбите, т.е. одна получается из другой некоторым преобразованием симметрии. Неподвижные точки поворота есть только у тождественного поворота и их штук. Тогда, по лемме Бёрнсайда, число орбит равняется , где минимальное число такое, что делится на , и число их раскрасок . Сумма же инвариантных раскрасок для всех поворотов: . В последней сумме слагаемых — функция Эйлера, для которых . Если же , то . Чтобы определить количество таких , меньших , нужно перебрать числа вида и проверять их на условие . Таких чисел, очевидно, (по определению ). Поэтому сумму можно заменить: .
Тогда .
Алгоритм решения задачи про ожерелья с отражениями
Пусть теперь ожерелья считаются одинаковыми, если они не только переходят друг в друга поворотом, но и отражением относительно некоторой оси (ось может проходить через две противоположные бусинки или через две противоположные пустоты в чётном случае и через бусинку и пустоту напротив неё в нечётном случае). Такие ожерелья называются bracelets [1]. Будем пользоваться леммой Бёрнсайда. Разберём два случая.
Для начала покажем, что в качестве операций требуется рассматривать только повороты и отражения.
- Поворот и отражение — отражение.
Занумеруем наши бусинки по часовой стрелке. Поворот и отражение не меняют порядка (в каком-то направлении бусинки занумерованы по порядку). Нетрудно понять, что отражение меняет направление обхода наших бусинок и не меняет порядка. Если мы сначала сделаем поворот, а потом отразим относительно какой-нибудь оси, то мы то самое же можем получить и обыкновенным отражением относительно какой-то оси. Такая ось найдётся, потому что всегда можно выбрать ось, что поставит первую бусинку на своё изначальное место, поменяв направление обхода (если перебирать все оси подряд, начиная с оси, проходящей через нужную нам бусинку, то изначально она останется на своём месте, потом сместится на одно место, потом на два и.т.д.). Поэтому поворот и отражение не добавляет нам новой операции.
- Отражение и поворот — отражение.
Аналогичные рассуждения.
- Отражение и отражение — поворот.
Тут мы дважды меняем направление обхода, но не меняем порядка. Поэтому данная операция заменяется обычным поворотом.
Пусть число бусинок нечётное, тогда мы имеем осей, проходящих через каждую бусинку. Рассмотрим одну ось. Возьмём половину бусинок с одной стороны от оси и ту бусинку, через которую проходит данная ось. Мы можем окрасить их в произвольные цвета, а остальная половина по ним однозначно восстановится. Таким образом количество неподвижных точек для одной оси будет . Операций в группе будет в два раза больше, чем было: ( сдвигов и отражений).
По Лемме Бёрнсайда:
. Первые операций — повороты, и сумма количества их неподвижных точек, делённая на , принимает значение , где - количество ожерелий из бусинок различных цветов без отражений (задача выше) т.к. деление в задаче без отражений происходило на , а здесь на . Следующие операций — отражения. У каждой такой операции неподвижных точек. Поэтому сумма получается .
Разберём теперь чётный случай.
Тут мы имеем осей, проходящих через пустоты между бусинками (ось можно провести через пустоту после каждой бусинки, но половина из них будет повторяться). В таких вот случаях можно выбрать по бусинок и дать им произвольные цвета. Остальная половина восстановится по ним. Таким образом для данных осей количество неподвижных точек будет .
Ещё у нас есть осей, проходящих через бусинки. В данных случаях мы можем выбрать по бусинок (бусинки на оси и все по одну какую-то сторону от неё). То есть будет неподвижных точек. Операций также .
По Лемме Бёрнсайда: