Матрица смежности графа — различия между версиями
(Добавлены категории) |
м (rollbackEdits.php mass rollback) |
||
| (не показана 51 промежуточная версия 7 участников) | |||
| Строка 1: | Строка 1: | ||
| − | + | __NOTOC__ | |
| − | '''Матрицей смежности''' (англ. Adjacency matrix) <tex>A=||\alpha_{i,j}||</tex> | + | {{Определение |
| + | |definition ='''Матрицей смежности''' ''(англ. Adjacency matrix)'' <tex>A=||\alpha_{i,j}||</tex> невзвешенного графа <tex>G=(V,E)</tex> называется матрица <tex>A_{[V\times{}V]}</tex>, в которой <tex>\alpha_{i,j}</tex> — количество рёбер, соединяющих вершины <tex>v_i</tex> и <tex>v_j</tex>, причём при <tex>i=j</tex> каждую петлю учитываем дважды, если граф не является ориентированным, и один раз, если граф ориентирован. | ||
| + | }} | ||
| − | === | + | {{Определение |
| + | |definition ='''Матрицей смежности''' ''(англ. Adjacency matrix)'' <tex>A=||\alpha_{i,j}||</tex> взвешенного графа <tex>G=(V,E)</tex> называется матрица <tex>A_{[V\times{}V]}</tex>, в которой <tex>\alpha_{i,j}</tex> — вес ребра, соединяющего вершины <tex>v_i</tex> и <tex>v_j</tex>. | ||
| + | }} | ||
| + | |||
| + | ====Примеры матриц смежности:==== | ||
{| border="1" cellpadding="5" cellspacing="0" style="text-align:center" | {| border="1" cellpadding="5" cellspacing="0" style="text-align:center" | ||
| − | !style="background:#f2f2f2"| | + | !style="background:#f2f2f2"|Взвешенность графа |
| + | !style="background:#f2f2f2"|Вид графа | ||
!style="background:#f2f2f2"|Матрица смежности | !style="background:#f2f2f2"|Матрица смежности | ||
|- | |- | ||
| − | |style="background:#f9f9f9"|[[Файл: | + | !style="background:#f2f2f2"|Не взвешенный граф |
| + | |style="background:#f9f9f9"|[[Файл: Adjacency matrix.png|180px]] | ||
|style="background:#f9f9f9"|<tex>\begin{pmatrix} | |style="background:#f9f9f9"|<tex>\begin{pmatrix} | ||
0 & 1 & 0 & 0 & 1\\ | 0 & 1 & 0 & 0 & 1\\ | ||
| Строка 14: | Строка 22: | ||
0 & 1 & 1 & 0 & 1\\ | 0 & 1 & 1 & 0 & 1\\ | ||
1 & 1 & 0 & 1 & 0\\ | 1 & 1 & 0 & 1 & 0\\ | ||
| + | \end{pmatrix}</tex> | ||
| + | |- | ||
| + | !style="background:#f2f2f2"|Взвешенный граф | ||
| + | !style="background:#f9f9f9"|[[Файл:weighted_graph.png|180px]] | ||
| + | |style="background:#f9f9f9"|<tex>\begin{pmatrix} | ||
| + | 0 & 40 & \infty & \infty & 18\\ | ||
| + | 40 & 0 & 22 & 6 & 15\\ | ||
| + | \infty & 22 & 0 & 14 & \infty \\ | ||
| + | \infty & 6 & 14 & 0 & 20\\ | ||
| + | 18 & 15 & \infty & 20 & 0 \\ | ||
\end{pmatrix}</tex> | \end{pmatrix}</tex> | ||
|} | |} | ||
| + | |||
| + | ==Оценка памяти и времени работы== | ||
| + | |||
| + | Матрица смежности занимает <tex>O(|V|^2)</tex> памяти. За <tex>O(1)</tex> можно определить вес ребра или его наличие между любыми двумя вершинами. Такой способ хранения графа хорошо подходит для плотных графов, в которых число рёбер между различными парами вершин <tex>\Omega(|V|^2)</tex>. | ||
== Свойства == | == Свойства == | ||
| − | Для графов без петель и кратных рёбер матрица смежности бинарна (состоит из нулей и единиц) | + | {{Утверждение |
| + | |statement=Для графов без петель и кратных рёбер матрица смежности бинарна (состоит из нулей и единиц). | ||
| + | }} | ||
| + | {{Утверждение | ||
| + | |statement=Для графов без петель и кратных рёбер главная диагональ матрицы смежности целиком состоит из нулей. | ||
| + | }} | ||
| + | |||
| + | {{Утверждение | ||
| + | |about=о сумме элементов строки матрицы смежности для ориентированного графа | ||
| + | |statement=Сумма элементов <tex>i</tex>-й строки равна <tex>deg^- v_i</tex>, то есть <tex>\sum\limits_{j=1}^{n}\alpha_{i,j} = deg^- v_i</tex>. | ||
| + | Аналогично сумма элементов <tex>j</tex>-го стоблца равна <tex>deg^+ v_j</tex>, то есть <tex>\sum\limits_{i=1}^{n}\alpha_{i,j} = deg^+ v_j</tex>. | ||
| + | }} | ||
| + | |||
| + | |||
| + | {{Утверждение | ||
| + | |about=о сумме элементов строки матрицы смежности для неориентированного графа | ||
| + | |statement=Матрица смежности является симметричной. | ||
| + | |proof= | ||
| + | Сумма элементов <tex>i</tex>-й строки равна <tex>deg \; v_i</tex>, то есть <tex>\sum\limits_{j=1}^{n}\alpha_{i,j} = deg \; v_i</tex>. Вследствие симметричности суммы элементов <tex>i</tex>-й строки и <tex>i</tex>-го столбца равны. | ||
| + | }} | ||
| + | |||
| − | |||
| − | |||
| − | |||
| − | === | + | {{Теорема |
| − | + | |about=о поиске количества путей заданной длины с помощью матрицы смежности ориентированного графа | |
| + | |statement= Пусть <tex>A_{[V\times{}V]}=\alpha_{i,j}</tex> — [[Матрица смежности графа|матрица смежности]] [[Основные определения: граф, ребро, вершина, степень, петля, путь, цикл|ориентированного графа]] <tex>G=(V,E)</tex> без петель и <tex>A^l=\gamma_{i,j}</tex>, где <tex>l\in\mathbb{N}</tex>. Тогда <tex>\gamma_{i,j}</tex> равно количеству путей <tex>v_i\leadsto{}v_j</tex> длины <tex>l</tex>. | ||
| − | + | |proof=Утверждение очевидно при <tex>l = 1</tex>. Пусть <tex>l > 1</tex>, и утверждение верно для <tex>l - 1</tex>. Тогда <tex>A^{l-1}=\varepsilon_{i,j}</tex>, где <tex>\varepsilon_{i,j}</tex> равно количеству путей <tex>v_i\leadsto{}v_j</tex> длины <tex>l-1</tex>. Следовательно, | |
| + | : <tex>\gamma_{i,j}=\sum\limits_{s=1}^{n}{\varepsilon_{i,s}\alpha_{s,j}}</tex> | ||
| + | равно числу путей <tex>v_i\leadsto{}v_j</tex> длины <tex>l</tex>, так как каждый такой маршрут состоит из путей <tex>v_i\leadsto{}v_s</tex> длины <tex>l-1</tex> и ребра, ведущего из предпоследней вершины <tex>v_s</tex> пути в его последнюю вершину <tex>v_j</tex>. | ||
| + | }} | ||
== См. также == | == См. также == | ||
| − | |||
* [[Матрица инцидентности графа]] | * [[Матрица инцидентности графа]] | ||
| − | == | + | |
| − | * Харари Фрэнк '''Теория графов''' | + | == Источники информации == |
| + | * Харари Фрэнк '''Теория графов''' Пер. с англ. и предисл. В. П. Козырева. Под ред. Г.П.Гаврилова. Изд. 2-е. — М.: Едиториал УРСС, 2003. — 296 с. — ISBN 5-354-00301-6 | ||
* Асанов М. О., Баранский В. А., Расин В. В. '''Дискретная математика: графы, матроиды, алгоритмы''' — НИЦ РХД, 2001. — 288 с. — ISBN 5-93972-076-5 | * Асанов М. О., Баранский В. А., Расин В. В. '''Дискретная математика: графы, матроиды, алгоритмы''' — НИЦ РХД, 2001. — 288 с. — ISBN 5-93972-076-5 | ||
| + | |||
[[Категория: Алгоритмы и структуры данных]] | [[Категория: Алгоритмы и структуры данных]] | ||
[[Категория: Основные определения теории графов]] | [[Категория: Основные определения теории графов]] | ||
Текущая версия на 19:20, 4 сентября 2022
| Определение: |
| Матрицей смежности (англ. Adjacency matrix) невзвешенного графа называется матрица , в которой — количество рёбер, соединяющих вершины и , причём при каждую петлю учитываем дважды, если граф не является ориентированным, и один раз, если граф ориентирован. |
| Определение: |
| Матрицей смежности (англ. Adjacency matrix) взвешенного графа называется матрица , в которой — вес ребра, соединяющего вершины и . |
Примеры матриц смежности:
| Взвешенность графа | Вид графа | Матрица смежности |
|---|---|---|
| Не взвешенный граф | 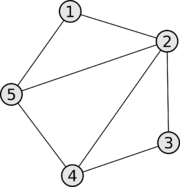
|
|
| Взвешенный граф | 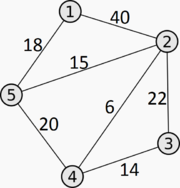
|
Оценка памяти и времени работы
Матрица смежности занимает памяти. За можно определить вес ребра или его наличие между любыми двумя вершинами. Такой способ хранения графа хорошо подходит для плотных графов, в которых число рёбер между различными парами вершин .
Свойства
| Утверждение: |
Для графов без петель и кратных рёбер матрица смежности бинарна (состоит из нулей и единиц). |
| Утверждение: |
Для графов без петель и кратных рёбер главная диагональ матрицы смежности целиком состоит из нулей. |
| Утверждение (о сумме элементов строки матрицы смежности для ориентированного графа): |
Сумма элементов -й строки равна , то есть .
Аналогично сумма элементов -го стоблца равна , то есть . |
| Утверждение (о сумме элементов строки матрицы смежности для неориентированного графа): |
Матрица смежности является симметричной. |
| Сумма элементов -й строки равна , то есть . Вследствие симметричности суммы элементов -й строки и -го столбца равны. |
| Теорема (о поиске количества путей заданной длины с помощью матрицы смежности ориентированного графа): |
Пусть — матрица смежности ориентированного графа без петель и , где . Тогда равно количеству путей длины . |
| Доказательство: |
|
Утверждение очевидно при . Пусть , и утверждение верно для . Тогда , где равно количеству путей длины . Следовательно, |
См. также
Источники информации
- Харари Фрэнк Теория графов Пер. с англ. и предисл. В. П. Козырева. Под ред. Г.П.Гаврилова. Изд. 2-е. — М.: Едиториал УРСС, 2003. — 296 с. — ISBN 5-354-00301-6
- Асанов М. О., Баранский В. А., Расин В. В. Дискретная математика: графы, матроиды, алгоритмы — НИЦ РХД, 2001. — 288 с. — ISBN 5-93972-076-5