Пересечение прямоугольника с множеством прямоугольников (PST) — различия между версиями
(Новая страница: «== Определение == Priority Search Tree позволяет решать следующую задачу. Даны <tex>n</tex> точек, а такж...») |
м (rollbackEdits.php mass rollback) |
||
| (не показано 7 промежуточных версий 4 участников) | |||
| Строка 1: | Строка 1: | ||
| + | [[Категория: Вычислительная геометрия]] | ||
== Определение == | == Определение == | ||
Priority Search Tree позволяет решать следующую задачу. Даны <tex>n</tex> точек, а также запросы. Каждый запрос характеризуется отрезком по одной координате <tex>[y_1, y_2]</tex>, а также числом <tex>x_q</tex> по другой координате. Для каждого запроса структура возвращает все точки, которые находятся в отрезке <tex>[y_1, y_2]</tex> по одной координате, и имеют другую координату не больше <tex>x_q</tex>. На каждый запрос дерево отвечает за <tex>O(\log\,n + k)</tex>, где <tex>k</tex> {{---}} количество точек в ответе. | Priority Search Tree позволяет решать следующую задачу. Даны <tex>n</tex> точек, а также запросы. Каждый запрос характеризуется отрезком по одной координате <tex>[y_1, y_2]</tex>, а также числом <tex>x_q</tex> по другой координате. Для каждого запроса структура возвращает все точки, которые находятся в отрезке <tex>[y_1, y_2]</tex> по одной координате, и имеют другую координату не больше <tex>x_q</tex>. На каждый запрос дерево отвечает за <tex>O(\log\,n + k)</tex>, где <tex>k</tex> {{---}} количество точек в ответе. | ||
| Строка 35: | Строка 36: | ||
Тут все сложнее. Представим, что мы ищем <tex>y_1</tex> и <tex>y_2</tex> (из запроса) в PST как в обычном дереве поиска по <tex>y</tex>. Рассмотрим все точки, которые лежат между двумя путями поиска. Среди них рассмотрим точки с <tex>x <= x_q</tex>. Ровно эти точки и есть ответ. Разобьем все вершины на три группы. Первая {{---}} вершины, которые лежат хотя бы на одном из двух путей. Их <tex>O(\log\,n)</tex>. Вторая {{---}} вершины, которые находятся между двумя путями. Третья {{---}} все остальные. Время обработки вершин первой группы не превышает <tex>O(\log\,n)</tex>. Как только мы зашли в вершину третей группы, сразу поймем, что отрезок по <tex>y</tex> не пересекается с запросом и выйдем. А зайти в них мы можем только из вершин, которые лежат на двух путях (а их <tex>O(\log\,n)</tex>). Отлично! Зайдя в вершину второй группы, мы либо ее добавим в ответ и продолжим, либо выйдем, так как единственная причина, почему корень не подошел {{---}} его <tex>x</tex> слишком большой, а, значит, и все вершины поддерева не подходят. В итоге их обработка занимает <tex>O(k)</tex>. В сумме все хорошо! | Тут все сложнее. Представим, что мы ищем <tex>y_1</tex> и <tex>y_2</tex> (из запроса) в PST как в обычном дереве поиска по <tex>y</tex>. Рассмотрим все точки, которые лежат между двумя путями поиска. Среди них рассмотрим точки с <tex>x <= x_q</tex>. Ровно эти точки и есть ответ. Разобьем все вершины на три группы. Первая {{---}} вершины, которые лежат хотя бы на одном из двух путей. Их <tex>O(\log\,n)</tex>. Вторая {{---}} вершины, которые находятся между двумя путями. Третья {{---}} все остальные. Время обработки вершин первой группы не превышает <tex>O(\log\,n)</tex>. Как только мы зашли в вершину третей группы, сразу поймем, что отрезок по <tex>y</tex> не пересекается с запросом и выйдем. А зайти в них мы можем только из вершин, которые лежат на двух путях (а их <tex>O(\log\,n)</tex>). Отлично! Зайдя в вершину второй группы, мы либо ее добавим в ответ и продолжим, либо выйдем, так как единственная причина, почему корень не подошел {{---}} его <tex>x</tex> слишком большой, а, значит, и все вершины поддерева не подходят. В итоге их обработка занимает <tex>O(k)</tex>. В сумме все хорошо! | ||
}} | }} | ||
| − | == | + | == Псевдокод == |
<code> | <code> | ||
struct PST | struct PST | ||
| Строка 70: | Строка 71: | ||
req(tree->up, y1, y2, x_max, ans) | req(tree->up, y1, y2, x_max, ans) | ||
</code> | </code> | ||
| + | |||
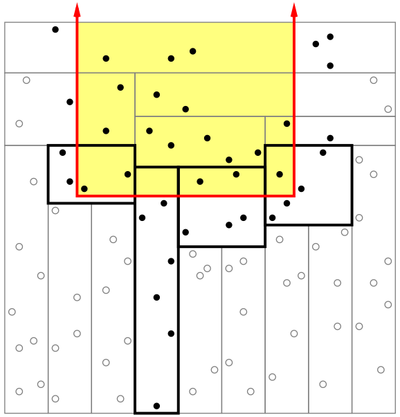
| + | == Причем тут пересечение прямоугольника с множеством прямоугольников? == | ||
| + | [[Файл:PSTVIEW.png|400px|thumb|left]] | ||
| + | Задача решается следующим образом. Будем находить ответ тремя разными способами, а их объединение и будет настоящим ответом. Будем считать, что объединение множеств можно делать за <tex>O(n)</tex>, где <tex>n</tex> {{---}} суммарное количество элементов в них. | ||
| + | |||
| + | '''Первый способ.''' Найдем все прямоугольники, в которых прямоугольник из запроса лежит полностью. Для этого нужно решать такую задачу. Дано множество прямоугольников, для заданной точки найти все прямоугольники, в которых она лежит. Это точно можно решать за <tex>O(\log^2\,n+answer)</tex> с помощью двухмерного [[Дерево интервалов (interval_tree) и пересечение точки с множеством интервалов | дерева интервалов]]. А может можно и проще. | ||
| + | |||
| + | '''Второй способ.''' Найдем все прямоугольники, которые полностью лежат внутри заданного в запросе. Для этого воспользуемся [[Перечисление_точек_в_произвольном_прямоугольнике_за_n_*_log_%5E(d_-_1)_n_(range_tree) | range tree]]. Просто для каждого прямоугольника добавим в range tree его левый верхний угол. Задав запрос в виде нашего прямоугольника, мы получим то, что и нужно. | ||
| + | |||
| + | '''Третий способ.''' Найдем все прямоугольники, хотя бы одна сторона которого пересекает заданный в запросе. Для этого воспользуемся [[Пересечение_прямоугольника_с_множеством_непересекающихся_отрезков_(segment_tree) | деревом отрезков]]. В структуру добавим все стороны всех прямоугольников и зададим запрос в виде нашего прямоугольника. | ||
| + | |||
| + | Утверждается, что все прямоугольники, которые нам нужны {{---}} объединение ответов, полученных тремя способами. Оценивать асимтотику всего этого мне совсем не хочется, но, наверное, это <tex>O(\log^2\,n+answer)</tex> времени на запрос. <tex>O(n\log\,n)</tex> памяти из-за range tree и <tex>O(n\log^2\,n)</tex> на построение. Но, возможно, я что-то забыл или что-то можно сделать более эффективно. | ||
Текущая версия на 19:39, 4 сентября 2022
Содержание
Определение
Priority Search Tree позволяет решать следующую задачу. Даны точек, а также запросы. Каждый запрос характеризуется отрезком по одной координате , а также числом по другой координате. Для каждого запроса структура возвращает все точки, которые находятся в отрезке по одной координате, и имеют другую координату не больше . На каждый запрос дерево отвечает за , где — количество точек в ответе.
Как строится?
Дерево строится рекурсивно. Выберем точку с наименьшей -координатой (если таких несколько, то из них выберем с наименьшим ). Все остальные точки отсортируем по и разобьем на две равные (количество может отличаться на один) части. Далее будем считать, что все точки первой части имеют координату меньше всех точек второй части (с одинаковыми поступаем как обычно — сравниваем по ). Для каждого из двух множеств, если оно не пусто, построим дерево рекурсивно.
| Теорема: |
PST занимает памяти. |
| Доказательство: |
| Каждая точка будет корнем ровно одного дерева. Количество деревьев не превышает количества точек. В сумме . |
| Теорема: |
Максимальная глубина PST . |
| Доказательство: |
| При рекурсивном вызове количество точек уменьшается как минимум в два раза. |
| Теорема: |
Построение PST работает за времени. |
| Доказательство: |
| Необходимо отсортировать точки по — для этого необходимо . Построение каждого дерева требует , где — количество точек в дереве, чтобы найти минимальную по точку, а также для построения новых списков точек для сыновей. На каждом уровне точек, уровней , значит, в сумме тоже . |
Как отвечать на запрос?
Если корня больше , то никакие точки дерева не могут быть в ответе. Будем хранить также минимальную и максимальную по точки, которые лежат в поддереве. Тогда, если отрезок запроса по не пересекается с отрезком по всех точек поддерева, то также никакие точки из дерева не должны быть добавлены в ответ. Если корень дерева лежит в нужном интервале, добавим его в ответ. Вызовем рекурсивно поиск ответа для двух сыновей.
| Теорема: |
Будет получен правильный ответ на запрос. |
| Доказательство: |
| Вроде бы очевидно. |
| Теорема: |
Ответ на запрос работает за , где — размер ответа. |
| Доказательство: |
| Тут все сложнее. Представим, что мы ищем и (из запроса) в PST как в обычном дереве поиска по . Рассмотрим все точки, которые лежат между двумя путями поиска. Среди них рассмотрим точки с . Ровно эти точки и есть ответ. Разобьем все вершины на три группы. Первая — вершины, которые лежат хотя бы на одном из двух путей. Их . Вторая — вершины, которые находятся между двумя путями. Третья — все остальные. Время обработки вершин первой группы не превышает . Как только мы зашли в вершину третей группы, сразу поймем, что отрезок по не пересекается с запросом и выйдем. А зайти в них мы можем только из вершин, которые лежат на двух путях (а их ). Отлично! Зайдя в вершину второй группы, мы либо ее добавим в ответ и продолжим, либо выйдем, так как единственная причина, почему корень не подошел — его слишком большой, а, значит, и все вершины поддерева не подходят. В итоге их обработка занимает . В сумме все хорошо! |
Псевдокод
struct PST point root point min_y, max_y PST *down, *up
// pts sorted by y
PST * build_PST(vector<point> pts)
if (pts.size() == 0)
return NULL
min_y = max_ y = root = min_element(pts) // by x
remove_element(pts, root)
int mid = pts.size() / 2
vector<point> down_pts = pts[0..mid]
vector<point> up_pts = pts[mid+1..pts.size() - 1]
down = build_PST(down_pts)
up = build_PST(up_pts)
if (down != NULL)
min_y = min(min_y, down->min_y)
if (up != NULL)
max_y = max(max_y, up->max_y)
void req(PST * tree, int y1, int y2, int x_max, vector<point> & ans)
if (tree == NULL)
return
if (x_max < tree->root.x)
return
if (y1 > tree->max_y || y2 < tree->min_y)
return
if (tree->root in [y1..y2]x[-inf;x_max])
answer.push_back(tree->root)
req(tree->down, y1, y2, x_max, ans)
req(tree->up, y1, y2, x_max, ans)
Причем тут пересечение прямоугольника с множеством прямоугольников?
Задача решается следующим образом. Будем находить ответ тремя разными способами, а их объединение и будет настоящим ответом. Будем считать, что объединение множеств можно делать за , где — суммарное количество элементов в них.
Первый способ. Найдем все прямоугольники, в которых прямоугольник из запроса лежит полностью. Для этого нужно решать такую задачу. Дано множество прямоугольников, для заданной точки найти все прямоугольники, в которых она лежит. Это точно можно решать за с помощью двухмерного дерева интервалов. А может можно и проще.
Второй способ. Найдем все прямоугольники, которые полностью лежат внутри заданного в запросе. Для этого воспользуемся range tree. Просто для каждого прямоугольника добавим в range tree его левый верхний угол. Задав запрос в виде нашего прямоугольника, мы получим то, что и нужно.
Третий способ. Найдем все прямоугольники, хотя бы одна сторона которого пересекает заданный в запросе. Для этого воспользуемся деревом отрезков. В структуру добавим все стороны всех прямоугольников и зададим запрос в виде нашего прямоугольника.
Утверждается, что все прямоугольники, которые нам нужны — объединение ответов, полученных тремя способами. Оценивать асимтотику всего этого мне совсем не хочется, но, наверное, это времени на запрос. памяти из-за range tree и на построение. Но, возможно, я что-то забыл или что-то можно сделать более эффективно.