Выпуклая оболочка в n-мерном пространстве — различия между версиями
м (rollbackEdits.php mass rollback) |
|||
| (не показано 6 промежуточных версий 4 участников) | |||
| Строка 5: | Строка 5: | ||
Выберем любые две точки <tex>p_1</tex> и <tex>p_2</tex>. Далее из оставшихся выберем точку <tex>p_3</tex>, которая не лежит на прямой, образованной точками <tex>p_1</tex> и <tex>p_2</tex>. После этого выберем точку <tex>p_4</tex>, которая не лежит на плоскости, образованной точками <tex>p_1, p_2</tex> и <tex>p_3</tex>. Если этого сделать не получилось, то запустим алгоритм для поиска выпуклой оболочки на плоскости. | Выберем любые две точки <tex>p_1</tex> и <tex>p_2</tex>. Далее из оставшихся выберем точку <tex>p_3</tex>, которая не лежит на прямой, образованной точками <tex>p_1</tex> и <tex>p_2</tex>. После этого выберем точку <tex>p_4</tex>, которая не лежит на плоскости, образованной точками <tex>p_1, p_2</tex> и <tex>p_3</tex>. Если этого сделать не получилось, то запустим алгоритм для поиска выпуклой оболочки на плоскости. | ||
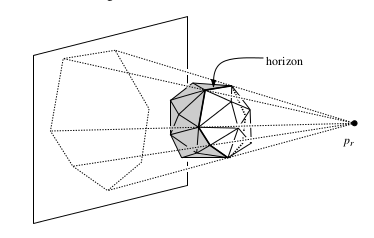
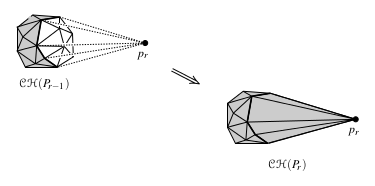
| − | Так мы получили тетраэдр <tex>p_1 p_2 p_3 p_4</tex>, который является выпуклой оболочкой этих четырёх точек. Сделаем random shuffle оставшихся точек <tex>p_5, ..., p_n</tex> и будем добавлять их по одной в выпуклую оболочку. Если <tex>p_i</tex> внутри или на границах выпуклой оболочки, то выпуклая оболочка не меняется на этом шаге. Иначе из имеющейся выпуклой оболочки надо удалить все видимые из данной точки грани и добавить новые — из точки до каждого ребра, образующего horizon (см. картинки; на них белые грани видны из точки <tex>p_r</tex>). После этого нужно смержить соседние грани, которые получились | + | Так мы получили тетраэдр <tex>p_1 p_2 p_3 p_4</tex>, который является выпуклой оболочкой этих четырёх точек. Сделаем random shuffle оставшихся точек <tex>p_5, ..., p_n</tex> и будем добавлять их по одной в выпуклую оболочку. Если <tex>p_i</tex> внутри или на границах выпуклой оболочки, то выпуклая оболочка не меняется на этом шаге. Иначе из имеющейся выпуклой оболочки надо удалить все видимые из данной точки грани и добавить новые — из точки до каждого ребра, образующего horizon (см. картинки; на них белые грани видны из точки <tex>p_r</tex>). После этого нужно смержить соседние грани, которые получились компланарными. |
[[Файл:3dconvexhullhorizon.png]] [[Файл:3dconvexhulladd.png]] | [[Файл:3dconvexhullhorizon.png]] [[Файл:3dconvexhulladd.png]] | ||
| Строка 14: | Строка 14: | ||
Для выяснения, какие грани видны из точки, будем хранить двудольный граф <tex>G</tex>, называемый conflict graph, в одной доле которого будут точки, которые ещё не добавлены в выпуклую оболочку, а в другой — имеющиеся на данный момент грани выпуклой оболочки. Ребро между точкой <tex>p</tex> и гранью <tex>f</tex> в этом графе означает, что из <tex>p</tex> видна <tex>f</tex>, то есть они находятся в конфликте (in conflict): они не могут сосуществовать в выпуклой оболочке. | Для выяснения, какие грани видны из точки, будем хранить двудольный граф <tex>G</tex>, называемый conflict graph, в одной доле которого будут точки, которые ещё не добавлены в выпуклую оболочку, а в другой — имеющиеся на данный момент грани выпуклой оболочки. Ребро между точкой <tex>p</tex> и гранью <tex>f</tex> в этом графе означает, что из <tex>p</tex> видна <tex>f</tex>, то есть они находятся в конфликте (in conflict): они не могут сосуществовать в выпуклой оболочке. | ||
| − | Инициализация графа для тетраэдра тривиальна: для каждой точки определяем, какие грани видны из неё. Далее на каждом шаге после добавления точки <tex>p_r</tex> удалим из графа соответствующие удаляемым из выпуклой оболочки граням вершины и инцидентные им рёбра: просто удаляем все достижимые из <tex>p_r</tex> вершины. Также удалим вершину, соответствующую <tex>p_r</tex>. Далее добавляем новые грани выпуклой оболочки. Необходимо найти их конфликты. Сами грани представляют из себя треугольники, если, конечно, они не были смержены с уже имеющимися гранями. Во втором случае новая грань находится в конфликте с теми же точками, что и старая грань, т.к. смерженные грани | + | Инициализация графа для тетраэдра тривиальна: для каждой точки определяем, какие грани видны из неё. Далее на каждом шаге после добавления точки <tex>p_r</tex> удалим из графа соответствующие удаляемым из выпуклой оболочки граням вершины и инцидентные им рёбра: просто удаляем все достижимые из <tex>p_r</tex> вершины. Также удалим вершину, соответствующую <tex>p_r</tex>. Далее добавляем новые грани выпуклой оболочки. Необходимо найти их конфликты. Сами грани представляют из себя треугольники, если, конечно, они не были смержены с уже имеющимися гранями. Во втором случае новая грань находится в конфликте с теми же точками, что и старая грань, т.к. смерженные грани компланарны. |
[[Файл:3dconvexhullconflictlist.png|200px|thumb|left]] | [[Файл:3dconvexhullconflictlist.png|200px|thumb|left]] | ||
| Строка 22: | Строка 22: | ||
{{Лемма | {{Лемма | ||
|id=lemma1 | |id=lemma1 | ||
| + | |about=1 | ||
|statement= | |statement= | ||
Пусть <tex>P</tex> — выпуклый многогранник с <tex>n</tex> вершинами. Тогда число его рёбер не превосходит <tex>3n - 6</tex>, а число его граней — <tex>2n - 4</tex>. | Пусть <tex>P</tex> — выпуклый многогранник с <tex>n</tex> вершинами. Тогда число его рёбер не превосходит <tex>3n - 6</tex>, а число его граней — <tex>2n - 4</tex>. | ||
|proof= | |proof= | ||
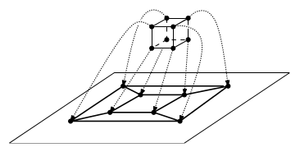
[[Файл:3dconvexhullprojection.png|300px|thumb|right|Верхняя грань куба спроецировалась на внешнюю грань графа]] | [[Файл:3dconvexhullprojection.png|300px|thumb|right|Верхняя грань куба спроецировалась на внешнюю грань графа]] | ||
| − | «Спроецируем» многогранник на плоскость, как на картинке. Получили планарный граф, по формуле Эйлера имеем <tex>n - n_e + n_f = 2</tex>, где <tex>n_e</tex> — число рёбер, <tex>n_f</tex> — число граней. Каждая грань нашего графа имеет по меньшей мере 3 ребра, каждое ребро инцидентно двум граням, поэтому имеем <tex>2 n_e \geqslant 3 n_f</tex>. Тогда получаем <tex>n_f \leqslant 2n - 4</tex>, и, подставив это в формулу Эйлера, <tex>n_e \leqslant 3n - 6</tex>. | + | «Спроецируем» многогранник на плоскость, как на картинке (будем считать общеизвестным фактом, что выпуклый многогранник планарен). Получили планарный граф, по формуле Эйлера имеем <tex>n - n_e + n_f = 2</tex>, где <tex>n_e</tex> — число рёбер, <tex>n_f</tex> — число граней. Каждая грань нашего графа имеет по меньшей мере 3 ребра, каждое ребро инцидентно двум граням, поэтому имеем <tex>2 n_e \geqslant 3 n_f</tex> (если не удаётся это понять, можно представить двудольный граф, где слева грани, а справа рёбра. Из каждого ребра исходит ровно 2 вершины, а в каждую грань входит хотя бы 3). Тогда получаем <tex>n_f \leqslant 2n - 4</tex>, и, подставив это в формулу Эйлера, <tex>n_e \leqslant 3n - 6</tex>. |
| + | }} | ||
| + | |||
| + | {{Лемма | ||
| + | |id=lemma2 | ||
| + | |about=2 | ||
| + | |statement= | ||
| + | Ожидаемое число граней, создаваемое нашим алгоритмом, не превосходит <tex>6n - 20</tex>. | ||
| + | |proof= | ||
| + | Рассмотрим добавление точки <tex>p_r</tex>. Все грани, добавленные на этом шаге алгоритма, инцидентны этой точке, равно как и добавленные рёбра. Обозначим число инцидентных точке <tex>p_i</tex> рёбер (степень вершины; оно же число инцидентных точек) в выпуклой оболочке <tex>r</tex> точек как <tex>k_{i, r}</tex>. | ||
| + | |||
| + | По [[#lemma1|лемме 1]] у многогранника с <tex>r</tex> веришнами не больше <tex>3r - 6</tex> рёбер. Значит, сумма степеней вершин многогранника не больше <tex>6r - 12</tex>. Значит, средняя степень вершины равна <tex>6 - 12/r</tex>. Точки берутся в случайном порядке, поэтому можно считать, что ожидаемая степень вершины <tex>p_r</tex> равна <tex>6 - 12/r</tex>. Это рассуждение верно только для <tex>r > 4</tex>, так как первые четыре точки фиксированы, их суммарная степень равна <tex>12</tex>. Посчитаем математическое ожидание <tex>k_r</tex>: | ||
| + | |||
| + | <tex>E(k_{r, r}) = \frac{1}{r - 4} \sum_{i = 5}^{r} k_{i, r} \leqslant \frac{1}{r - 4} ( \sum_{i = 1}^{r} k_{i, r} - 12 ) \leqslant \frac{6r - 12 - 12}{r - 4} = 6</tex>. | ||
| + | |||
| + | Ожидаемое число граней — это число граней в начальном тетраэдре (4 — ваш К.О.) плюс ожидаемое общее число созданных граней при добавлении точек. Поэтому искомое число равно <tex>4 + \sum_{r = 5}^{n} E(k_{r, r}) \leqslant 4 + 6(n - 4) = 6n - 20</tex>. | ||
| + | }} | ||
| + | |||
| + | {{Теорема | ||
| + | |statement= | ||
| + | Время работы алгоритма — <tex>O(n \log n)</tex>. | ||
| + | |proof= | ||
| + | Шаги перед добавлением точек можно сделать за <tex>O(n \log n)</tex>. Очередной шаг требует константного времени, если <tex>m_r</tex> — число конфликтных граней для добавляемой точки — равно нулю (то есть когда точка внутри или на границах имеющейся выпуклой оболочки). Иначе этот шаг требует <tex>O(m_r)</tex> времени плюс время на удаление видимых рёбер (удалить ребро можно не больше одного раза, поэтому можно считать, что этот шаг лишь изменит константу во времени создания новых рёбер) и изменение графа конфликтов. | ||
| + | |||
| + | Заметим, что <tex>m_r</tex> — число граней, удалённых на очередном шаге алгоритма, поэтому по [[#lemma2|лемме 2]] <tex>E(\sum_{r = 5}^{n} m_r) = O(n)</tex>. | ||
| + | |||
| + | При изменении графа конфликтов на шаге <tex>r</tex> требуется время, равное сумме числа конфликтных точек для смежных граней каждого ребра на horizon. Это меньше либо равно числу всех конфликтных точек для всех граней. Утверждается, что оно равно <tex>O(n \log n)</tex>, и это надо как-то доказать (в де Берге есть, надо разобраться и дополнить), и тогда теорема доказана. | ||
}} | }} | ||
Текущая версия на 19:23, 4 сентября 2022
| Конспект написан не до конца, но основные вещи уже есть. |
Рассмотрим трёхмерный случай. -мерный сводится к трёхмерному.
Суть алгоритма
Выберем любые две точки и . Далее из оставшихся выберем точку , которая не лежит на прямой, образованной точками и . После этого выберем точку , которая не лежит на плоскости, образованной точками и . Если этого сделать не получилось, то запустим алгоритм для поиска выпуклой оболочки на плоскости.
Так мы получили тетраэдр , который является выпуклой оболочкой этих четырёх точек. Сделаем random shuffle оставшихся точек и будем добавлять их по одной в выпуклую оболочку. Если внутри или на границах выпуклой оболочки, то выпуклая оболочка не меняется на этом шаге. Иначе из имеющейся выпуклой оболочки надо удалить все видимые из данной точки грани и добавить новые — из точки до каждого ребра, образующего horizon (см. картинки; на них белые грани видны из точки ). После этого нужно смержить соседние грани, которые получились компланарными.
Детали реализации
Будем хранить выпуклую оболочку в виде DCEL.
Для выяснения, какие грани видны из точки, будем хранить двудольный граф , называемый conflict graph, в одной доле которого будут точки, которые ещё не добавлены в выпуклую оболочку, а в другой — имеющиеся на данный момент грани выпуклой оболочки. Ребро между точкой и гранью в этом графе означает, что из видна , то есть они находятся в конфликте (in conflict): они не могут сосуществовать в выпуклой оболочке.
Инициализация графа для тетраэдра тривиальна: для каждой точки определяем, какие грани видны из неё. Далее на каждом шаге после добавления точки удалим из графа соответствующие удаляемым из выпуклой оболочки граням вершины и инцидентные им рёбра: просто удаляем все достижимые из вершины. Также удалим вершину, соответствующую . Далее добавляем новые грани выпуклой оболочки. Необходимо найти их конфликты. Сами грани представляют из себя треугольники, если, конечно, они не были смержены с уже имеющимися гранями. Во втором случае новая грань находится в конфликте с теми же точками, что и старая грань, т.к. смерженные грани компланарны.
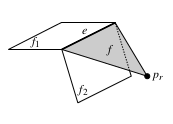
Перейдём к первому случаю. Пусть мы добавили точку и рассматриваем грань . — ребро, принадлежащее horizon, — грани, пересечение которых образовывало в старой оболочке. Пусть — ещё не добавленная точка, из которой видно , тогда из неё видно и ребро , причём как в новой, так и в старой выпуклой оболочке (так как новая включает в себя старую). Но это возможно, только если из видно или . Значит, точки, с которыми у есть конфликт — это только какие-то из точек, у которых есть конфликт у и .
Время работы
| Лемма (1): |
Пусть — выпуклый многогранник с вершинами. Тогда число его рёбер не превосходит , а число его граней — . |
| Доказательство: |
| «Спроецируем» многогранник на плоскость, как на картинке (будем считать общеизвестным фактом, что выпуклый многогранник планарен). Получили планарный граф, по формуле Эйлера имеем , где — число рёбер, — число граней. Каждая грань нашего графа имеет по меньшей мере 3 ребра, каждое ребро инцидентно двум граням, поэтому имеем (если не удаётся это понять, можно представить двудольный граф, где слева грани, а справа рёбра. Из каждого ребра исходит ровно 2 вершины, а в каждую грань входит хотя бы 3). Тогда получаем , и, подставив это в формулу Эйлера, . |
| Лемма (2): |
Ожидаемое число граней, создаваемое нашим алгоритмом, не превосходит . |
| Доказательство: |
|
Рассмотрим добавление точки . Все грани, добавленные на этом шаге алгоритма, инцидентны этой точке, равно как и добавленные рёбра. Обозначим число инцидентных точке рёбер (степень вершины; оно же число инцидентных точек) в выпуклой оболочке точек как . По лемме 1 у многогранника с веришнами не больше рёбер. Значит, сумма степеней вершин многогранника не больше . Значит, средняя степень вершины равна . Точки берутся в случайном порядке, поэтому можно считать, что ожидаемая степень вершины равна . Это рассуждение верно только для , так как первые четыре точки фиксированы, их суммарная степень равна . Посчитаем математическое ожидание : . Ожидаемое число граней — это число граней в начальном тетраэдре (4 — ваш К.О.) плюс ожидаемое общее число созданных граней при добавлении точек. Поэтому искомое число равно . |
| Теорема: |
Время работы алгоритма — . |
| Доказательство: |
|
Шаги перед добавлением точек можно сделать за . Очередной шаг требует константного времени, если — число конфликтных граней для добавляемой точки — равно нулю (то есть когда точка внутри или на границах имеющейся выпуклой оболочки). Иначе этот шаг требует времени плюс время на удаление видимых рёбер (удалить ребро можно не больше одного раза, поэтому можно считать, что этот шаг лишь изменит константу во времени создания новых рёбер) и изменение графа конфликтов. Заметим, что — число граней, удалённых на очередном шаге алгоритма, поэтому по лемме 2 . При изменении графа конфликтов на шаге требуется время, равное сумме числа конфликтных точек для смежных граней каждого ребра на horizon. Это меньше либо равно числу всех конфликтных точек для всех граней. Утверждается, что оно равно , и это надо как-то доказать (в де Берге есть, надо разобраться и дополнить), и тогда теорема доказана. |