Link-Cut Tree — различия между версиями
Lena (обсуждение | вклад) (→min(v)) |
м (rollbackEdits.php mass rollback) |
||
| (не показано 100 промежуточных версий 10 участников) | |||
| Строка 1: | Строка 1: | ||
| − | ''' | + | '''Динамические деревья''' (англ.''dynamic tree'') используются в двух областях: [[Определение сети, потока|потоки]] и динамические графы. |
| − | * '''min(v)''' - искать минимум на пути от вершины до корня | + | В первом случае динамические деревья позволяют построить эффективные алгоритмы для задачи о поиске максимального потока. |
| − | * '''add(v, c)''' - прибавлять константу на пути от вершины до корня | + | В динамическом графе периодически происходят изменения: появляются и исчезают ребра, меняются их веса. Нужно быстро обрабатывать изменения, а также уметь [[Отношение связности, компоненты связности | проверять связность]], [[Алгоритмы на деревьях|искать диаметр]]. Динамические деревья являются инструментом, который позволяет легко решать эти задачи. Динамические деревья особенно эффективны, когда нужно работать с большими деревьями и большим количеством запросов '''link''' и '''cut'''. |
| − | * '''link(u,w)''' - подвешивать одно дерево на другое | + | |
| − | * '''cut(v)''' - отрезать дерево с корнем в вершине v. | + | '''Link-cut tree''' {{---}} это структура данных, которая хранит [[Дерево, эквивалентные определения |лес деревьев]] и позволяет выполнять следующие операции: |
| − | Среднее время выполнения каждой операции - <tex>O(log | + | * '''<tex>\mathrm{min(v)}</tex>''' {{---}} искать минимум на пути от вершины до корня, |
| + | * '''<tex>\mathrm{add(v, c)}</tex>''' {{---}} прибавлять константу на пути от вершины до корня, | ||
| + | * '''<tex>\mathrm{link(u, w)}</tex>''' {{---}} подвешивать одно дерево на другое, | ||
| + | * '''<tex>\mathrm{cut(v)}</tex>''' {{---}} отрезать дерево с корнем в вершине <tex>\mathrm{v}</tex>. | ||
| + | Среднее время выполнения каждой операции {{---}} <tex>O(\log n)</tex>. Эта структура данных была придумана Робертом Тарьяном и Даниелем Слейтером в 1982 году. | ||
==Решение задачи в частном случае== | ==Решение задачи в частном случае== | ||
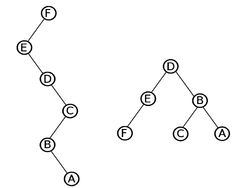
| − | Сначала | + | Сначала рассмотрим частный случай, в котором все деревья {{---}} это пути, и мы хотим уметь: |
| − | + | ||
| + | [[Файл:Path_to_tree.png|250px|thumb|right|Пример построения дерева для пути]] | ||
| + | * '''<tex>\mathrm{add(v, c)}</tex>''' и '''<tex>\mathrm{min(v)}</tex>''' {{---}} прибавлять константу и искать минимум на некотором суффиксе (то есть на пути от вершины до корня), | ||
| + | * '''<tex>\mathrm{cut(v)}</tex>''' {{---}} разбить один путь на два, | ||
| + | * '''<tex>\mathrm{link(v, u)}</tex>''' {{---}} подвешивать голову одного пути к хвосту другого. | ||
| + | |||
| + | Если бы не последние две операции, то можно было бы применить [[Несогласованные поддеревья. Реализация массового обновления|дерево отрезков]], сложив в него вершины в том порядке в котором они идут в пути. Но непонятно, как сливать или разрезать деревья отрезков. Эту задачу можно решить при помощи [[Декартово дерево по неявному ключу|декартового дерева по неявному ключу]]. Также, если использовать какие-нибудь сливаемые деревья, то <tex>\mathrm{link}</tex> и <tex> \mathrm{cut}</tex> реализуются просто. Осталось научиться искать минимум и прибавлять константу на пути. Для этого, как и в деревьях отрезков, будем хранить дополнительные значения в вершинах. | ||
| + | В качестве сливаемых деревьев выберем [[Splay-дерево|splay-деревья]], в которых ключи выбираются равными глубине вершины. | ||
| + | |||
| + | Тогда операции <tex>\mathrm{cut}</tex> будет соответствовать <tex>\mathrm{split}</tex>. | ||
| + | |||
| + | <tex>\mathrm{link(path1, path2)}</tex> соединяет голову первого пути с хвостом второго. Используем функцию <tex>\mathrm{merge(path2, path1)}</tex>, которая вызовет <tex>\mathrm{splay}</tex> от хвоста второго пути и сделает первый путь правым ребенком корня <tex>\mathrm{path2}</tex>, то есть теперь <tex>\mathrm{path1}</tex> находится ниже, чем <tex>\mathrm{path2}</tex>. | ||
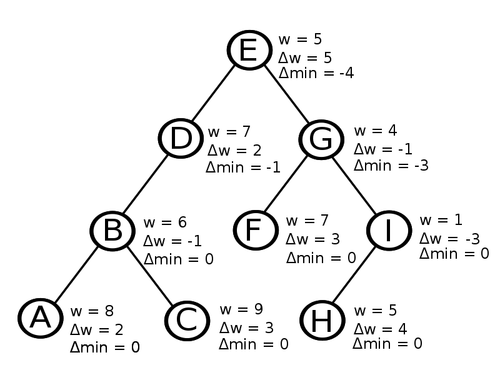
Чтобы прибавлять заданное число на пути от вершины до корня, будем в каждой вершине хранить величину <tex>\Delta w</tex>, которая равна разнице между весом вершины и весом её родителя. Для корня это значение равно весу самого корня. Поэтому вес вершины определятся следующим образом: | Чтобы прибавлять заданное число на пути от вершины до корня, будем в каждой вершине хранить величину <tex>\Delta w</tex>, которая равна разнице между весом вершины и весом её родителя. Для корня это значение равно весу самого корня. Поэтому вес вершины определятся следующим образом: | ||
| − | <tex>w(u) = \ | + | <tex>w(u) = \displaystyle \sum_v^{} \Delta w(v)</tex>, где <tex> v </tex> {{---}} все предки вершины <tex> u </tex>. |
| − | При прибавлении <tex>\alpha</tex> на пути от вершины <tex>v</tex> до корня, сначала вызывается <tex>splay(v)</tex>, после чего в левом поддереве находятся вершины, которые лежат на пути к корню. Затем надо прибавить <tex>\alpha</tex> к <tex>\Delta w(v)</tex> и, чтобы сохранить веса вершин, которые находятся ниже в пути, вычесть <tex>\alpha</tex> от <tex>\Delta w(right(v))</tex>. | + | При прибавлении <tex>\alpha</tex> на пути от вершины <tex>v</tex> до корня, сначала вызывается <tex>\mathrm{splay(v)}</tex>, после чего в левом поддереве находятся вершины, которые лежат на пути к корню. Затем надо прибавить <tex>\alpha</tex> к <tex>\Delta w(v)</tex> и, чтобы сохранить веса вершин, которые находятся ниже в пути, вычесть <tex>\alpha</tex> от <tex>\Delta w(right(v))</tex>. |
| − | |||
| − | |||
| − | <tex>min | + | Для реализации <tex>\min</tex> будем хранить минимум уже для всего поддерева. Чтобы искать минимум от вершины <tex>v</tex>, надо вызвать <tex>\mathrm{splay(v)}</tex> и сравнить её вес с минимумом левого поддерева, в котором теперь находятся все вершины пути кроме <tex>v</tex>. Определим <tex>\Delta \min (v)</tex> таким образом, чтобы сохранялся следующий инвариант: <tex>\min (v) = \Delta \min (v) + w(v) </tex>. Пусть <tex>l</tex> и <tex>r</tex> дети <tex>v</tex>, тогда |
| − | <tex>\ | + | <tex>\min (v) = \min \{w(v), \min(l), \min(r)\}</tex> |
| − | |||
| − | |||
| − | |||
| − | + | <tex>\Delta \min(v) = \min(v) - w(v) \\ | |
| + | = \min\{w(v) - w(v), \min(l) - w(v), \min(r) - w(v)\} \\ | ||
| + | = \min\{0, \ (\Delta \min(l) + w(l)) - w(v), \ (\Delta \min(r) + w(r)) - w(v)\} \\ | ||
| + | = \min\{0, \ \Delta \min(l) + \Delta w(l), \ \Delta \min(r) + \Delta w(r)\}</tex> | ||
| + | |||
| + | [[Файл:Linkcut_weights.png|500px]] | ||
==Link-cut tree== | ==Link-cut tree== | ||
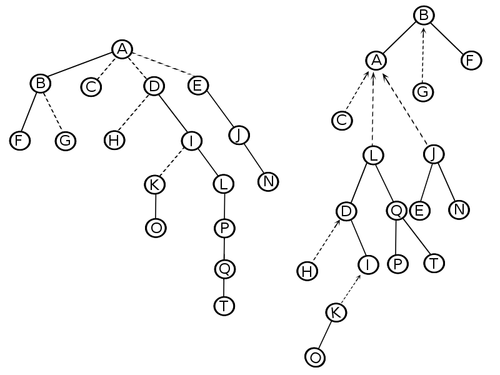
| − | Чтобы обобщить, разобьем дерево на множество непересекающихся путей. Каждое ребро обозначим либо | + | Чтобы обобщить, разобьем дерево на множество непересекающихся путей. Каждое ребро обозначим либо сплошным, либо пунктирным. Все пути в link-cut дереве хранятся в виде splay-деревьев. Корень каждого splay-дерева хранит указатель на вершину-родителя. В дальнейшем будем называть этот указатель <tex>pathparent</tex>. |
[[Файл:Linkcut_paths.png|500px||center|Разбиение дерева на пути]] | [[Файл:Linkcut_paths.png|500px||center|Разбиение дерева на пути]] | ||
===expose(u)=== | ===expose(u)=== | ||
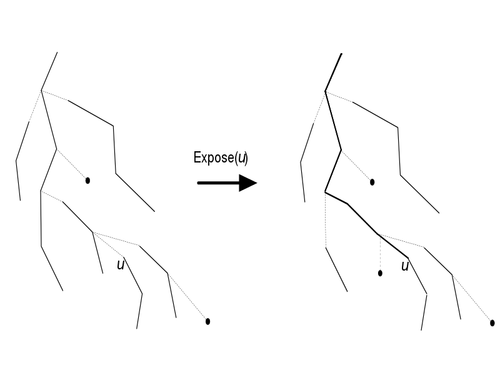
| − | Ключевая операция в link-cut-деревьях {{---}} <tex>expose(u)</tex>. После её выполнения <tex>u</tex> лежит на одном пути с корнем link-cut дерева и при этом становится корнем в splay-дереве получившегося пути. | + | Ключевая операция в link-cut-деревьях {{---}} <tex>\mathrm{expose(u)}</tex>. После её выполнения <tex>u</tex> лежит на одном пути с корнем link-cut дерева и при этом становится корнем в splay-дереве получившегося пути. Для этого она поднимается вверх по link-cut дереву, и если какой-нибудь путь пересекает путь от <tex>u</tex> до корня, то она его отрезает, разъединяя splay-дерево и делая соответствующее сплошное ребро пунктирным ребром. |
[[Файл:Linkcut_expose.png|500px||center|Разбиение дерева на пути]] | [[Файл:Linkcut_expose.png|500px||center|Разбиение дерева на пути]] | ||
| − | '''expose(u | + | '''function''' expose(u: '''tree'''): |
splay(u) | splay(u) | ||
| − | v < | + | v <tex>=</tex> u |
| − | while | + | '''while''' v <tex> \ne </tex> root |
| − | p < | + | p <tex>=</tex> pathparent(v) <font color=green>//получаем указатель на ближайшую вершину пути, пересекающего путь от u до корня</font> |
splay(p) <font color=green>//теперь в правом поддереве p находятся вершины пути, которые находятся ниже чем p в link-cut-дереве,</font> | splay(p) <font color=green>//теперь в правом поддереве p находятся вершины пути, которые находятся ниже чем p в link-cut-дереве,</font> | ||
| − | parent(right(p)) < | + | parent(right(p)) <tex>=</tex> null <font color=green>//поэтому правое поддерево p делаем новым путем</font> |
| − | pathparent(right(p)) < | + | pathparent(right(p)) <tex>=</tex> p |
| − | right(p) < | + | right(p) <tex>=</tex> v <font color=green>//объединяем оставшийся и построенный пути</font> |
| − | + | <tex>\vartriangle</tex>w(v) -= <tex>\vartriangle</tex>w(p) | |
| − | + | <tex>\vartriangle</tex>min(p) <tex>=</tex> min{0, <tex>\vartriangle</tex>min(left(p)) + <tex>\vartriangle</tex>w(left(p)), <tex>\vartriangle</tex>min(right(p)) + <tex>\vartriangle</tex>w(right(p))} | |
| − | pathparent(v) < | + | pathparent(v) <tex>=</tex> null |
| − | v < | + | v <tex>=</tex> p |
splay(u) | splay(u) | ||
===add(v, c)=== | ===add(v, c)=== | ||
| − | Чтобы прибавить константу на пути от <tex>v</tex> до корня link-cut-дерева вызовем <tex>expose(v)</tex>, что построит запрашиваемый путь в виде splay-дерева, в котором <tex>v</tex> - корень, и в левом поддереве находятся вершины, которые находятся выше чем <tex>v</tex> в link-cut-дереве (то есть все вершины пути без <tex>v</tex>), а в правом - те, что ниже. Тогда прибавим <tex>c</tex> к <tex>\Delta w(v)</tex> и вычтем константу от правого ребенка <tex>v</tex>, чтобы скомпенсировать разницу и сохранить инвариант. | + | Чтобы прибавить константу на пути от <tex>v</tex> до корня link-cut-дерева вызовем <tex>\mathrm{expose(v)}</tex>, что построит запрашиваемый путь в виде splay-дерева, в котором <tex>v</tex> {{---}} корень, и в левом поддереве находятся вершины, которые находятся выше чем <tex>v</tex> в link-cut-дереве (то есть все вершины пути без <tex>v</tex>), а в правом {{---}} те, что ниже. Тогда прибавим <tex>c</tex> к <tex>\Delta w(v)</tex> и вычтем константу от правого ребенка <tex>v</tex>, чтобы скомпенсировать разницу и сохранить инвариант. |
| − | add(v, c) | + | '''function''' add(v: '''tree''', c: '''int'''): |
expose(v) | expose(v) | ||
| − | + | <tex>\vartriangle</tex>w(v) += c | |
| − | + | <tex>\vartriangle</tex>w(right(v)) -= c | |
| + | |||
===min(v)=== | ===min(v)=== | ||
| − | Построим splay-дерево для пути и сравним | + | Построим splay-дерево для пути и сравним вес корня <tex>v</tex> c минимумом в левом поддереве: |
| − | '''min(v)''' | + | '''function''' min(v: '''tree'''): '''int''' |
expose(v) | expose(v) | ||
| − | if | + | '''if''' <tex>\vartriangle</tex>min(left(v)) + <tex>\vartriangle</tex>w(left(v)) < <tex>\vartriangle</tex>w(v) |
| − | + | '''return''' <tex>\vartriangle</tex>min(left(v)) + <tex>\vartriangle</tex>w(left(v)) | |
| − | return | + | '''else''' |
| − | else | + | '''return''' <tex>\vartriangle</tex>w(v) |
| − | return | ||
===link(v, u)=== | ===link(v, u)=== | ||
| − | Если <tex>v</tex> - корень, а <tex>u</tex> - вершина в другом дереве, то <tex>link(v, u)</tex> соединяет два дерева добавлением ребра <tex>(v, u)</tex>, причем <tex> | + | Если <tex>v</tex> {{---}} корень, а <tex>u</tex> {{---}} вершина в другом дереве, то <tex>\mathrm{link(v, u)}</tex> соединяет два дерева добавлением ребра <tex>(v, u)</tex>, причем <tex>v</tex> становится родителем <tex>u</tex>. |
| − | '''link(v, u)''' | + | '''function''' link(v: '''tree''', u: '''tree'''): '''tree''' |
| − | expose(v) <font color=green> //теперь v - корень в splay-дереве пути и не имеет левого ребенка(так как ключ равен глубине в link-cut дереве)</font> | + | expose(v) <font color=green> //теперь v {{---}} корень в splay-дереве пути и не имеет левого ребенка(так как ключ равен глубине в link-cut дереве)</font> |
expose(u) | expose(u) | ||
| − | + | <tex>\vartriangle</tex>w(u) -= <tex>\vartriangle</tex>w(v) <font color=green>//чтобы сделать u родителем v в link-cut дереве 1. делаем путь, содержащий u, левым ребенком v в splay-дереве</font> | |
| − | parent(u) < | + | parent(u) <tex>=</tex> v <font color=green>// 2. обновляем <tex>\vartriangle</tex>w, <tex>\vartriangle</tex>min</font> |
| − | left(v) < | + | left(v) <tex>=</tex> u |
| − | + | <tex>\vartriangle</tex>min(v) <tex>=</tex> min{0, <tex>\vartriangle</tex>min(u) + <tex>\vartriangle</tex>w(u), <tex>\vartriangle</tex>min(right(v)) + <tex>\vartriangle</tex>w((right(v)))} | |
| + | '''return''' v | ||
===cut(v)=== | ===cut(v)=== | ||
| − | Отрезает дерево с корнем <tex>v</tex>. После вызова <tex>expose(v) | + | Отрезает дерево с корнем <tex>v</tex>. После вызова <tex>\mathrm{expose(v)}</tex> вершина <tex>v</tex> станет корнем splay-дерева, и в правом поддереве будут содержаться все вершины, которые были ниже <tex>v</tex> в link-cut дереве, а в левом {{---}} те что выше. Обнулив указатель на левого ребенка <tex>v</tex> и на родителя в левом поддереве, получим требуемое. |
| − | '''cut(v | + | '''function''' cut(v: '''tree'''): |
expose(v) | expose(v) | ||
| − | + | <tex>\vartriangle</tex>w(left(v)) += <tex>\vartriangle</tex>w(v) | |
| − | + | <tex>\vartriangle</tex>min(v) <tex>=</tex> min{0, <tex>\vartriangle</tex>min(right(v)) + <tex>\vartriangle</tex>w(right(v))} | |
| − | left(v) < | + | parent(left(v)) <tex>=</tex> null |
| − | + | left(v) <tex>=</tex> null | |
==Оценка времени работы== | ==Оценка времени работы== | ||
| − | Назовем ребро из <tex>u</tex> в её родителя <tex>v</tex> тяжелым, если количество детей <tex>u</tex> <tex>d(u) > \ | + | Назовем ребро из <tex>u</tex> в её родителя <tex>v</tex> тяжелым, если количество детей <tex>u</tex> равное <tex>d(u) > \dfrac{1}{2} d(v)</tex>. |
{{Лемма | {{Лемма | ||
|id = Lemma1 | |id = Lemma1 | ||
| − | |statement= На пути от вершины до корня не больше <tex>log | + | |statement= На пути от вершины до корня не больше <tex>\log n</tex> легких ребер. |
| + | |||
| + | |proof = Пусть <tex>m</tex> {{---}} количество вершин в дереве с корнем в вершине, в которой мы сейчас находимся. Поднимаясь по легкому ребру, <tex>m</tex> увеличивается в два раза, поэтому, пройдя больше <tex>\log n</tex> легких ребер, получим <tex>m > n</tex>. Значит, в дереве не больше <tex>\log n</tex> легких ребер. | ||
| + | }} | ||
| − | Операция <tex>u</tex> осуществляется с помощью последовательности преобразований | + | Операция <tex>\mathrm{expose(u)}</tex> осуществляется с помощью последовательности преобразований пунктирного ребра в сплошное ребро и другого сплошного ребра в пунктирное ребро. Обозначим количество таких преобразований за <tex>M</tex>. Найдем количество преобразований сделанных в течение <tex>\mathrm{expose(u)}</tex>. Пусть <tex>H</tex> {{---}} множество всех тяжелых ребер, <tex>L</tex> {{---}} все легкие ребра, <tex>S \rightarrow D</tex> {{---}} множество сплошных ребер, преобразованных в пунктирные в течение одного <tex>\mathrm{expose}</tex>, <tex>D \rightarrow S</tex> {{---}} множество пунктирных ребер, преобразованных в сплошные. |
<tex>M = |\{D \rightarrow S\}| = |\{L \cap D \rightarrow S\}| + |\{H \cap D \rightarrow S\}|</tex> | <tex>M = |\{D \rightarrow S\}| = |\{L \cap D \rightarrow S\}| + |\{H \cap D \rightarrow S\}|</tex> | ||
| − | По лемме, количество легких | + | По лемме, количество легких пунктирных ребер, преобразованных в сплошные, будет не больше, чем <tex>\log n</tex>. |
| − | Обозначим за <tex>F</tex> лес деревьев, в которых каждое ребро либо | + | Обозначим за <tex>F</tex> лес деревьев, в которых каждое ребро либо сплошное, либо пунктирное, a <tex>F'</tex> {{---}} лес, получившийся из <tex>F</tex> после одного вызова <tex>\mathrm{expose}</tex>. Определим потенциал <tex>\Phi _{a}(F) = n - 1 - |\{H \cap solid-edges\}|</tex>, <tex>\Delta \Phi _{a}</tex> {{---}} увеличение <tex>\Phi _{a}</tex> после одной операции <tex>\mathrm{expose}</tex>. |
{{Лемма | {{Лемма | ||
| Строка 112: | Строка 131: | ||
= M + |H \cap S \rightarrow D| - |H \cap D \rightarrow S| \\ | = M + |H \cap S \rightarrow D| - |H \cap D \rightarrow S| \\ | ||
\leqslant M + |L \cap D \rightarrow S| - |H \cap D \rightarrow S| \\ | \leqslant M + |L \cap D \rightarrow S| - |H \cap D \rightarrow S| \\ | ||
| − | = 2 \ | + | = 2 \cdot |L \cap D \rightarrow S| \\ |
| − | =2 \ | + | =2 \cdot \log n |
</tex> | </tex> | ||
}} | }} | ||
| − | Теперь проанализируем <tex>M</tex>. Используя тот факт, что начальное значение <tex>\Phi _{a}</tex> не превосходит <tex>n - 1</tex>, приходим к тому, что для деревьев с <tex>n</tex> вершинами, по крайней мере за <tex>n - 1</tex> операцию <tex>expose</tex>, среднее <tex>M</tex> на одну операцию будет не больше, чем <tex>1 + 2\log n</tex> | + | Теперь проанализируем <tex>M</tex>. Используя тот факт, что начальное значение <tex>\Phi _{a}</tex> не превосходит <tex>n - 1</tex>, приходим к тому, что для деревьев с <tex>n</tex> вершинами, по крайней мере за <tex>n - 1</tex> операцию <tex>\mathrm{expose}</tex>, среднее <tex>M</tex> на одну операцию будет не больше, чем <tex>1 + 2\log n</tex>. |
| + | |||
| + | Докажем, что [[Амортизационный анализ|амортизационная стоимость операции]] <tex>\mathrm{expose}</tex> равна <tex>O(\log n)</tex>. | ||
| + | |||
| + | Пусть <tex>s(v)</tex> {{---}} количество вершин в поддеревьях <tex>v</tex> ( здесь имеется в виду splay-дерево пути, который строится в ходе выполнения <tex>\mathrm{expose}</tex>), <tex>r(v) = \log s(v)</tex>. По [[Splay-дерево#Lemma1|лемме]] стоимость ''i''-той операции <tex>\mathrm{splay}</tex> не превосходит <tex>1 + 3 \cdot (r(t) - r(v))</tex>. Это приводит к тому, что амортизационная стоимость <tex>\mathrm{expose}</tex> ограничена следующим значением: | ||
| + | |||
| + | <tex>3 \cdot \log n - 3 \cdot \log (s(v)) + M</tex> | ||
| + | |||
| + | Здесь <tex>M = O(\log n)</tex>, поэтому амортизационная стоимость <tex>\mathrm{expose}</tex> равна <tex>O(\log n)</tex>. | ||
| + | |||
| + | ==Применение== | ||
| + | ===LCA=== | ||
| + | C помощью link-cut-дерева можно найти наименьшего общего предка: | ||
| + | '''function''' lca(u: '''tree''', v: '''tree'''): '''tree''' | ||
| + | expose(u) | ||
| + | expose(v) | ||
| + | '''return''' pathparent(splay(u)) | ||
| + | |||
| + | Первый вызов <tex>\mathrm{expose}</tex> построит путь от <tex>u</tex> до корня. Второй пересечет этот путь в наименьшем общем предке, поэтому в splay-дереве, которому принадлежит <tex>u</tex>, хранится указатель <tex>pathparent</tex> на <tex>\mathrm{lca}</tex>, после <tex>\mathrm{splay}(u)</tex> он будет находиться в <tex>u</tex>. | ||
| − | + | ==См. также== | |
| + | * [[Метод двоичного подъема]] | ||
| + | * [[Алгоритм Тарьяна поиска LCA за O(1) в оффлайн]] | ||
| + | * [[Алгоритм Шибера-Вишкина]] | ||
| − | + | ==Источники информации== | |
| + | * [http://www.lektorium.tv/lecture/14464 А.С. Станкевич, "Дополнительные главы алгоритмов"] | ||
| + | * [https://sites.google.com/site/indy256/algo/link-cut-tree-lca Реализация LCA на link-cut дереве] | ||
| + | * [http://www.cs.cmu.edu/~sleator/papers/dynamic-trees.pdf D. Sleator and R. Tarjan, "A Data Structure for Dynamic Trees"] | ||
| + | * [http://compgeom.cs.uiuc.edu/~jeffe/teaching/datastructures/2006/notes/07-linkcut.pdf Jeff Erickson. Lecture 7. Link-Cut Trees] | ||
| + | * [http://planarity.org/Klein_splay_trees_and_link-cut_trees.pdf Optimization Algorithms for Planar Graphs. Splay trees and link-cut trees] | ||
| + | * [http://en.wikipedia.org/wiki/Link/cut_tree Wikipedia {{---}} Link/cut tree] | ||
| − | |||
| − | + | [[Категория: Алгоритмы и структуры данных]] | |
| + | [[Категория: Задача о наименьшем общем предке]] | ||
Текущая версия на 19:05, 4 сентября 2022
Динамические деревья (англ.dynamic tree) используются в двух областях: потоки и динамические графы. В первом случае динамические деревья позволяют построить эффективные алгоритмы для задачи о поиске максимального потока. В динамическом графе периодически происходят изменения: появляются и исчезают ребра, меняются их веса. Нужно быстро обрабатывать изменения, а также уметь проверять связность, искать диаметр. Динамические деревья являются инструментом, который позволяет легко решать эти задачи. Динамические деревья особенно эффективны, когда нужно работать с большими деревьями и большим количеством запросов link и cut.
Link-cut tree — это структура данных, которая хранит лес деревьев и позволяет выполнять следующие операции:
- — искать минимум на пути от вершины до корня,
- — прибавлять константу на пути от вершины до корня,
- — подвешивать одно дерево на другое,
- — отрезать дерево с корнем в вершине .
Среднее время выполнения каждой операции — . Эта структура данных была придумана Робертом Тарьяном и Даниелем Слейтером в 1982 году.
Содержание
Решение задачи в частном случае
Сначала рассмотрим частный случай, в котором все деревья — это пути, и мы хотим уметь:
- и — прибавлять константу и искать минимум на некотором суффиксе (то есть на пути от вершины до корня),
- — разбить один путь на два,
- — подвешивать голову одного пути к хвосту другого.
Если бы не последние две операции, то можно было бы применить дерево отрезков, сложив в него вершины в том порядке в котором они идут в пути. Но непонятно, как сливать или разрезать деревья отрезков. Эту задачу можно решить при помощи декартового дерева по неявному ключу. Также, если использовать какие-нибудь сливаемые деревья, то и реализуются просто. Осталось научиться искать минимум и прибавлять константу на пути. Для этого, как и в деревьях отрезков, будем хранить дополнительные значения в вершинах. В качестве сливаемых деревьев выберем splay-деревья, в которых ключи выбираются равными глубине вершины.
Тогда операции будет соответствовать .
соединяет голову первого пути с хвостом второго. Используем функцию , которая вызовет от хвоста второго пути и сделает первый путь правым ребенком корня , то есть теперь находится ниже, чем .
Чтобы прибавлять заданное число на пути от вершины до корня, будем в каждой вершине хранить величину , которая равна разнице между весом вершины и весом её родителя. Для корня это значение равно весу самого корня. Поэтому вес вершины определятся следующим образом:
, где — все предки вершины .
При прибавлении на пути от вершины до корня, сначала вызывается , после чего в левом поддереве находятся вершины, которые лежат на пути к корню. Затем надо прибавить к и, чтобы сохранить веса вершин, которые находятся ниже в пути, вычесть от .
Для реализации будем хранить минимум уже для всего поддерева. Чтобы искать минимум от вершины , надо вызвать и сравнить её вес с минимумом левого поддерева, в котором теперь находятся все вершины пути кроме . Определим таким образом, чтобы сохранялся следующий инвариант: . Пусть и дети , тогда
Link-cut tree
Чтобы обобщить, разобьем дерево на множество непересекающихся путей. Каждое ребро обозначим либо сплошным, либо пунктирным. Все пути в link-cut дереве хранятся в виде splay-деревьев. Корень каждого splay-дерева хранит указатель на вершину-родителя. В дальнейшем будем называть этот указатель .
expose(u)
Ключевая операция в link-cut-деревьях — . После её выполнения лежит на одном пути с корнем link-cut дерева и при этом становится корнем в splay-дереве получившегося пути. Для этого она поднимается вверх по link-cut дереву, и если какой-нибудь путь пересекает путь от до корня, то она его отрезает, разъединяя splay-дерево и делая соответствующее сплошное ребро пунктирным ребром.
function expose(u: tree):
splay(u)
v u
while v root
p pathparent(v) //получаем указатель на ближайшую вершину пути, пересекающего путь от u до корня
splay(p) //теперь в правом поддереве p находятся вершины пути, которые находятся ниже чем p в link-cut-дереве,
parent(right(p)) null //поэтому правое поддерево p делаем новым путем
pathparent(right(p)) p
right(p) v //объединяем оставшийся и построенный пути
w(v) -= w(p)
min(p) min{0, min(left(p)) + w(left(p)), min(right(p)) + w(right(p))}
pathparent(v) null
v p
splay(u)
add(v, c)
Чтобы прибавить константу на пути от до корня link-cut-дерева вызовем , что построит запрашиваемый путь в виде splay-дерева, в котором — корень, и в левом поддереве находятся вершины, которые находятся выше чем в link-cut-дереве (то есть все вершины пути без ), а в правом — те, что ниже. Тогда прибавим к и вычтем константу от правого ребенка , чтобы скомпенсировать разницу и сохранить инвариант.
function add(v: tree, c: int):
expose(v)
w(v) += c
w(right(v)) -= c
min(v)
Построим splay-дерево для пути и сравним вес корня c минимумом в левом поддереве:
function min(v: tree): int
expose(v)
if min(left(v)) + w(left(v)) < w(v)
return min(left(v)) + w(left(v))
else
return w(v)
link(v, u)
Если — корень, а — вершина в другом дереве, то соединяет два дерева добавлением ребра , причем становится родителем .
function link(v: tree, u: tree): tree
expose(v) //теперь v — корень в splay-дереве пути и не имеет левого ребенка(так как ключ равен глубине в link-cut дереве)
expose(u)
w(u) -= w(v) //чтобы сделать u родителем v в link-cut дереве 1. делаем путь, содержащий u, левым ребенком v в splay-дереве
parent(u) v // 2. обновляем w, min
left(v) u
min(v) min{0, min(u) + w(u), min(right(v)) + w((right(v)))}
return v
cut(v)
Отрезает дерево с корнем . После вызова вершина станет корнем splay-дерева, и в правом поддереве будут содержаться все вершины, которые были ниже в link-cut дереве, а в левом — те что выше. Обнулив указатель на левого ребенка и на родителя в левом поддереве, получим требуемое.
function cut(v: tree):
expose(v)
w(left(v)) += w(v)
min(v) min{0, min(right(v)) + w(right(v))}
parent(left(v)) null
left(v) null
Оценка времени работы
Назовем ребро из в её родителя тяжелым, если количество детей равное .
| Лемма: |
На пути от вершины до корня не больше легких ребер. |
| Доказательство: |
| Пусть — количество вершин в дереве с корнем в вершине, в которой мы сейчас находимся. Поднимаясь по легкому ребру, увеличивается в два раза, поэтому, пройдя больше легких ребер, получим . Значит, в дереве не больше легких ребер. |
Операция осуществляется с помощью последовательности преобразований пунктирного ребра в сплошное ребро и другого сплошного ребра в пунктирное ребро. Обозначим количество таких преобразований за . Найдем количество преобразований сделанных в течение . Пусть — множество всех тяжелых ребер, — все легкие ребра, — множество сплошных ребер, преобразованных в пунктирные в течение одного , — множество пунктирных ребер, преобразованных в сплошные.
По лемме, количество легких пунктирных ребер, преобразованных в сплошные, будет не больше, чем .
Обозначим за лес деревьев, в которых каждое ребро либо сплошное, либо пунктирное, a — лес, получившийся из после одного вызова . Определим потенциал , — увеличение после одной операции .
| Лемма: |
| Доказательство: |
Теперь проанализируем . Используя тот факт, что начальное значение не превосходит , приходим к тому, что для деревьев с вершинами, по крайней мере за операцию , среднее на одну операцию будет не больше, чем .
Докажем, что амортизационная стоимость операции равна .
Пусть — количество вершин в поддеревьях ( здесь имеется в виду splay-дерево пути, который строится в ходе выполнения ), . По лемме стоимость i-той операции не превосходит . Это приводит к тому, что амортизационная стоимость ограничена следующим значением:
Здесь , поэтому амортизационная стоимость равна .
Применение
LCA
C помощью link-cut-дерева можно найти наименьшего общего предка:
function lca(u: tree, v: tree): tree
expose(u)
expose(v)
return pathparent(splay(u))
Первый вызов построит путь от до корня. Второй пересечет этот путь в наименьшем общем предке, поэтому в splay-дереве, которому принадлежит , хранится указатель на , после он будет находиться в .