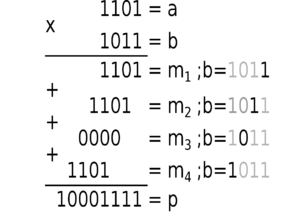Матричный умножитель — различия между версиями
м (rollbackEdits.php mass rollback) |
|||
| (не показано 96 промежуточных версий 9 участников) | |||
| Строка 1: | Строка 1: | ||
| − | == | + | == Принцип работы == |
| + | ==== Умножение в бинарной системе ==== | ||
| + | [[Файл:mult_bin.png|300px|right|thumb|''Умножение в столбик'']] | ||
| − | Матричный умножитель - | + | Умножение в бинарной системе счисления происходит точно так же, как в десятичной {{---}} по схеме ''умножения столбиком''. |
| + | Если множимое {{---}} <tex>k</tex> разрядное, а множитель {{---}} <tex>n</tex> разрядный, то для формирования произведения требуется вычислить <tex>n</tex> частичных произведений и сложить их между собой. | ||
| + | |||
| + | ===== Вычисление частичных произведений ===== | ||
| + | В бинарной системе для вычисления частичного произведения можно воспользоваться логическими элементами <tex>\&</tex> {{---}} конъюнкторами. | ||
| + | Каждое частичное произведение <tex>(m_i)</tex> {{---}} это результат выполнения <tex>k</tex> логических операции <tex>\&</tex> ( между текущим <tex>i</tex>, где <tex>i=1..n</tex>, разрядом множителя и всеми <tex>k</tex> разрядами множимого) и сдвига результата логической операции влево на число разрядов, соответствующее весу текущего разряда множителя. Матричный умножитель вычисляет частичные произведения по формуле: | ||
| + | |||
| + | <tex>m_i = 2^{i - 1} (a \& b_i), (i=1..n)</tex> | ||
| + | |||
| + | ===== Суммирование частичных произведений ===== | ||
| + | На этом этапе происходит сложение всех частичных произведений <tex> m </tex>. | ||
| + | |||
| + | ==== Схема ==== | ||
| + | [[Файл:Mult_3.png|700px|right|thumb|Схема матричного умножителя]] | ||
| + | Принципиальная схема умножителя, реализующая алгоритм двоичного умножения в столбик для двух четырёх {{---}} разрядных чисел приведена на рисунке. | ||
| + | Формирование частичных произведений осуществляется посредством логических элементов <tex>\&</tex>. | ||
| + | Полные одноразрядные сумматоры обеспечивают формирование разрядов результата. | ||
| + | Разрядность результата {{---}} <tex>l</tex> определяется разрядностью множителя {{---}} <tex>n</tex> и множимого {{---}} <tex>k</tex>: | ||
| + | |||
| + | <tex> l=n+k </tex>. | ||
| − | |||
| − | + | Все конъюнкторы работают параллельно. | |
| + | Полные одноразрядные сумматоры обеспечивают поразрядное сложение результатов конъюнкций и переносов из предыдущих разрядов сумматора. | ||
| + | В приведенной схеме использованы четырех разрядные сумматоры с последовательным переносом. | ||
| + | Время выполнения операции умножения определяется временем распространения переносов до выходного разряда <tex> p8 </tex>. | ||
| − | ==== | + | ==== '''Матричный умножитель''' ==== |
| − | + | Если внимательно посмотреть на схему '''матричного умножителя''' (англ. ''binary multiplier''), то можно увидеть, что она образует матрицу, сформированную проводниками, по которым передаются разряды числа <tex>A</tex> и числа <tex>B</tex>. В точках пересечения этих проводников находятся логические элементы <tex>\&</tex>. Именно по этой причине умножители, реализованные по данной схеме, получили название матричных умножителей. | |
| − | <tex> | ||
| − | |||
| − | |||
| − | |||
==Схемная сложность== | ==Схемная сложность== | ||
| − | Частичные произведения вычисляются за n шагов | + | Частичные произведения вычисляются за <tex>n</tex> шагов. Сложение с вычислением переносов включает <tex>n - 1</tex> шаг. Последнее сложение можно выполнить за <tex>O(\log n)</tex>. |
| − | В итоге суммарное время работы: < | + | |
| − | O(n) + O(n) + O(log n) = O(n) < | + | В итоге суммарное время работы: |
| − | + | ||
| + | <tex>O(n) + O(n) + O(\log n) = O(n) </tex> | ||
| + | |||
| + | Время работы схемы можно сократить, если сумматоры располагать не последовательно друг за другом, как это предполагается алгоритмом, приведенным на первом рисунке (общая схема), а суммировать частичные произведения попарно, затем суммировать пары частичных произведений и т.д. В этом случае время выполнения операции умножения значительно сократится. | ||
| − | == | + | Особенно заметен выигрыш в быстродействии при построении многоразрядных умножителей, однако ничего не бывает бесплатно. В обмен на быстродействие придётся заплатить увеличением разрядности сумматоров, а значит сложностью схемы. |
| + | |||
| + | Есть и более быстрые способы умножения двух чисел, например умножение с помощью [[дерево Уоллеса|дерева Уоллеса]], которое работает <tex>O(\log n)</tex>. | ||
| + | |||
| + | == См. также == | ||
| + | *[[Дерево Уоллеса]] | ||
| + | *[[Двоичный каскадный сумматор]] | ||
| + | |||
| + | == Источники информации == | ||
| + | * [http://bookfi.net/book/556972 Е. Угрюмов "Цифровая схемотехника" 2001г.] | ||
| + | |||
| + | * [http://bookfi.net/book/532753 Дк. Ф. Уэйкерли "Проектирование цифровых устройств, том 1." 2002г.] | ||
| + | |||
| + | * [http://bookfi.net/book/637011 М.И. Богданович "Цифровые интегральные микросхемы" 1996г.] | ||
| + | |||
| + | * [http://library.espec.ws/section6/article46.html Схема умножителя] | ||
* ''[http://ru.wikipedia.org/wiki/Кормен Кормен Т.], [http://ru.wikipedia.org/wiki/Лейзерсон,_Чарльз_Эрик Лейзерсон Ч.], [http://ru.wikipedia.org/wiki/Ривест,_Рональд_Линн Ривест Р.]''. Алгоритмы: построение и анализ = Introduction to Algorithms / Пер. с англ. под ред. А. Шеня. — М.: МЦНМО, 2000. — 960 с. — ISBN 5-900916-37-5 | * ''[http://ru.wikipedia.org/wiki/Кормен Кормен Т.], [http://ru.wikipedia.org/wiki/Лейзерсон,_Чарльз_Эрик Лейзерсон Ч.], [http://ru.wikipedia.org/wiki/Ривест,_Рональд_Линн Ривест Р.]''. Алгоритмы: построение и анализ = Introduction to Algorithms / Пер. с англ. под ред. А. Шеня. — М.: МЦНМО, 2000. — 960 с. — ISBN 5-900916-37-5 | ||
| + | |||
| + | [[Категория: Дискретная математика и алгоритмы]] | ||
| + | |||
| + | [[Категория: Схемы из функциональных элементов ]] | ||
Текущая версия на 19:27, 4 сентября 2022
Содержание
Принцип работы
Умножение в бинарной системе
Умножение в бинарной системе счисления происходит точно так же, как в десятичной — по схеме умножения столбиком. Если множимое — разрядное, а множитель — разрядный, то для формирования произведения требуется вычислить частичных произведений и сложить их между собой.
Вычисление частичных произведений
В бинарной системе для вычисления частичного произведения можно воспользоваться логическими элементами — конъюнкторами. Каждое частичное произведение — это результат выполнения логических операции ( между текущим , где , разрядом множителя и всеми разрядами множимого) и сдвига результата логической операции влево на число разрядов, соответствующее весу текущего разряда множителя. Матричный умножитель вычисляет частичные произведения по формуле:
Суммирование частичных произведений
На этом этапе происходит сложение всех частичных произведений .
Схема
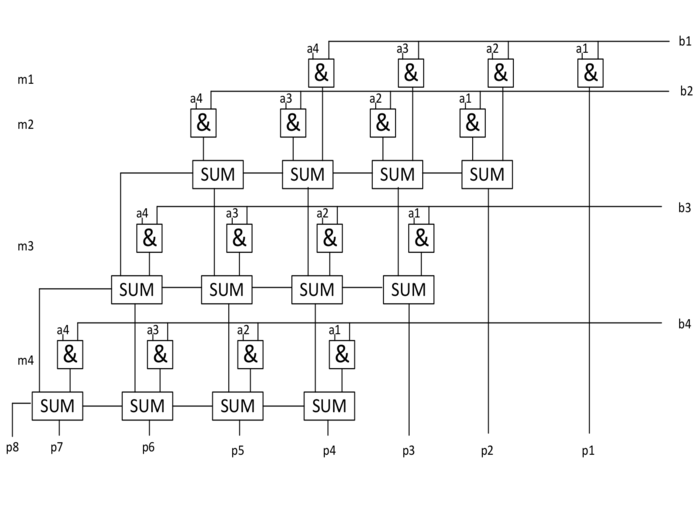
Принципиальная схема умножителя, реализующая алгоритм двоичного умножения в столбик для двух четырёх — разрядных чисел приведена на рисунке. Формирование частичных произведений осуществляется посредством логических элементов . Полные одноразрядные сумматоры обеспечивают формирование разрядов результата. Разрядность результата — определяется разрядностью множителя — и множимого — :
.
Все конъюнкторы работают параллельно.
Полные одноразрядные сумматоры обеспечивают поразрядное сложение результатов конъюнкций и переносов из предыдущих разрядов сумматора.
В приведенной схеме использованы четырех разрядные сумматоры с последовательным переносом.
Время выполнения операции умножения определяется временем распространения переносов до выходного разряда .
Матричный умножитель
Если внимательно посмотреть на схему матричного умножителя (англ. binary multiplier), то можно увидеть, что она образует матрицу, сформированную проводниками, по которым передаются разряды числа и числа . В точках пересечения этих проводников находятся логические элементы . Именно по этой причине умножители, реализованные по данной схеме, получили название матричных умножителей.
Схемная сложность
Частичные произведения вычисляются за шагов. Сложение с вычислением переносов включает шаг. Последнее сложение можно выполнить за .
В итоге суммарное время работы:
Время работы схемы можно сократить, если сумматоры располагать не последовательно друг за другом, как это предполагается алгоритмом, приведенным на первом рисунке (общая схема), а суммировать частичные произведения попарно, затем суммировать пары частичных произведений и т.д. В этом случае время выполнения операции умножения значительно сократится.
Особенно заметен выигрыш в быстродействии при построении многоразрядных умножителей, однако ничего не бывает бесплатно. В обмен на быстродействие придётся заплатить увеличением разрядности сумматоров, а значит сложностью схемы.
Есть и более быстрые способы умножения двух чисел, например умножение с помощью дерева Уоллеса, которое работает .
См. также
Источники информации
- Кормен Т., Лейзерсон Ч., Ривест Р.. Алгоритмы: построение и анализ = Introduction to Algorithms / Пер. с англ. под ред. А. Шеня. — М.: МЦНМО, 2000. — 960 с. — ISBN 5-900916-37-5