Straight skeleton — различия между версиями
Shersh (обсуждение | вклад) (→Алгоритм с изпользованием SLAV) |
м (rollbackEdits.php mass rollback) |
||
| (не показаны 92 промежуточные версии 3 участников) | |||
| Строка 1: | Строка 1: | ||
| − | + | Структура <tex>\mathrm{straight}\ \mathrm{skeleton}</tex> была придумана Oswin Aichholzer. Она используется в различных практических задачах (проектирование крыш для зданий), для доказательства некоторых теорем<ref>[http://en.wikipedia.org/wiki/Fold-and-cut_theorem Wikipedia {{---}} Fold-and-cut theorem]</ref>, в обработке изображений {{---}} эрозия и дилатация, но самое главное {{---}} можно оффсетить полигоны и упрощать их. | |
== Топологические свойства == | == Топологические свойства == | ||
| − | {{ | + | Далее будет дано процедурное определение <tex>\mathrm{straight}\ \mathrm{skeleton}</tex>. |
| − | |||
| − | |||
| − | |||
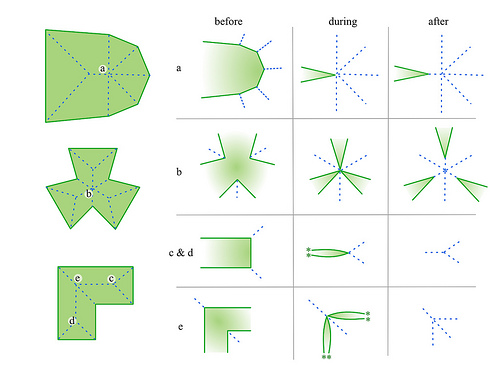
| − | + | Можно представить, будто все стороны многоугольника параллельно двигаются внутрь с одинаковой постоянной скоростью, то есть многоугольник как бы сжимается внутрь. Тогда {{Acronym | вершины будут двигаться вдоль биссектрис внутренних углов | Очевидный факт}}, а точки пересечения биссектрис будут являться точками, в которых рёбра полностью сократятся (выродятся в точку). В каждый момент времени от начала движения рёбер получается слоистая структура (рис 1.). На рис. 2 синим цветом выделен <tex> \mathrm{straight}\ \mathrm{skeleton} </tex> {{---}} множество отрезков, образованных точками пересечения при движении сторон полигона. Эта структура напоминает построение крыши для дома (рис. 3), и, в самом деле, скелетон применяется для решения подобных задач: по стенам здания необходимо спроектировать его крышу. | |
{| cellpadding="3" style="margin-left: auto; margin-right: auto;" | {| cellpadding="3" style="margin-left: auto; margin-right: auto;" | ||
| Строка 16: | Строка 13: | ||
[[Файл:Straight_roof.png|500px|center|thumb|Проектирование крыши здания по готовым стенам]] | [[Файл:Straight_roof.png|500px|center|thumb|Проектирование крыши здания по готовым стенам]] | ||
| − | + | Процесс стягивания многоугольника продолжается до тех пор, пока все рёбра не сожмутся в точку, то есть пока меняется число вершин в стянутом многоугольнике, и таким образом появляются новые вершины <tex> \mathrm{straight}\ \mathrm{skeleton} </tex>. Существуют два типа изменений, в ходе которых они образуются: | |
* <tex> Edge\ event </tex> {{---}} данное изменение происходит, когда сторона многоугольника полностью стягивается, делая соседние стороны инцидентными. | * <tex> Edge\ event </tex> {{---}} данное изменение происходит, когда сторона многоугольника полностью стягивается, делая соседние стороны инцидентными. | ||
| − | * <tex> Split\ event </tex> {{---}} происходит, когда ребро разбивается на два новых ребра, исходящих из точки преломления старого. Такое событие происходит на биссектрисе вогнутой вершины многоугольника. И тогда стягиваемая многоугольником область может | + | * <tex> Split\ event </tex> {{---}} происходит, когда ребро разбивается на два новых ребра, исходящих из точки преломления старого. Такое событие происходит на биссектрисе вогнутой вершины многоугольника. И тогда стягиваемая многоугольником область может разбиваться на две непересекающиеся многоугольные области. |
| − | На рисунке <tex>edge\ event'</tex>ы | + | На рисунке <tex>edge\ event'</tex>ы отмечены зелёными окружностями, а <tex>split\ event'</tex>ы {{---}} красными квадратами. |
[[Файл:skeleton_event_example.jpg|400px]] | [[Файл:skeleton_event_example.jpg|400px]] | ||
| − | Таким образом, | + | Таким образом, можно предъявить соответствие между элементами <tex> \mathrm{straight}\ \mathrm{skeleton} </tex> и происходящими событиями: |
| + | * внутренние вершины {{---}} <tex> event' </tex>ы, | ||
| + | * листья {{---}} вершины исходного многоугольника, | ||
| + | * грани {{---}} области многоугольника, заметаемые сторонами многоугольника в процессе стягивания, | ||
| + | * дуги {{---}} соединяют либо две внутренние вершины, либо внутреннюю вершину с листом. | ||
Стоит также отметить, что в общем случае <tex> split\ event'</tex>ы могут быть нетривиальными. На рисунке ниже в случае <tex> (c) </tex> в вершине <tex> p </tex> совпали <tex>split\ event</tex> из вершины <tex> u </tex> и ребра <tex> e </tex> и <tex> edge\ event</tex> ребра <tex> uv </tex>, а в случае <tex> (d) </tex> совпали два <tex> split\ event'</tex>а вершин <tex> u_1 </tex> и <tex> u_2 </tex>. Случаи <tex> (a) </tex> и <tex> (b) </tex> {{---}} простые <tex> edge </tex> и <tex> split\ event'</tex>ы. | Стоит также отметить, что в общем случае <tex> split\ event'</tex>ы могут быть нетривиальными. На рисунке ниже в случае <tex> (c) </tex> в вершине <tex> p </tex> совпали <tex>split\ event</tex> из вершины <tex> u </tex> и ребра <tex> e </tex> и <tex> edge\ event</tex> ребра <tex> uv </tex>, а в случае <tex> (d) </tex> совпали два <tex> split\ event'</tex>а вершин <tex> u_1 </tex> и <tex> u_2 </tex>. Случаи <tex> (a) </tex> и <tex> (b) </tex> {{---}} простые <tex> edge </tex> и <tex> split\ event'</tex>ы. | ||
| Строка 30: | Строка 31: | ||
[[Файл:Event_example.png]] | [[Файл:Event_example.png]] | ||
| − | Задача построения такого <tex> \mathrm{straight}\ \mathrm{skeleton} </tex> является частным случаем задачи построения <tex> \mathrm{weighted}\ \mathrm{straight}\ \mathrm{skeleton} </tex>, где каждому ребру можно задавать ''вес'', то есть скорость движения ребра. И эта скорость может быть даже отрицательной. | + | Задача построения такого <tex> \mathrm{straight}\ \mathrm{skeleton} </tex> является частным случаем задачи построения <tex> \mathrm{weighted}\ \mathrm{straight}\ \mathrm{skeleton} </tex>, где каждому ребру можно задавать ''вес'', то есть скорость движения ребра. И эта скорость может быть даже отрицательной. Но задача построения <tex>\mathrm{WSS}</tex> является в общем случае неопределённой. В процессе её решения возникают неоднозначности<ref>[http://twak.blogspot.ru/2009/05/ambiguous-weighted-skeleton.html Ambiguous weighted skeleton]</ref>. Задача <tex> \mathrm{weighted}\ \mathrm{straight}\ \mathrm{skeleton} </tex> является более сложной, и здесь рассматриваться не будет. |
| + | |||
| + | Алгоритм построения <tex> \mathrm{straight}\ \mathrm{skeleton} </tex> можно модифицировать, чтобы ''волновой фронт'' шёл от полигона. То есть сначала можно построить <tex> \mathrm{straight}\ \mathrm{skeleton} </tex>, тем самым упростив структуру полигона и сделав его более "гладким", а затем распространить волну в обратную сторону. | ||
== Свойства Straight skeleton == | == Свойства Straight skeleton == | ||
| − | Из процесса построения <tex> \mathrm{straight}\ \mathrm{skeleton} </tex> следует, что он является [[Укладка графа на плоскости#defplanar | планарным графом]]. Ранее уже упоминалось, что он также является [[Дерево, эквивалентные определения#tree |деревом]]. Будем обозначать <tex> \mathrm{straight}\ \mathrm{skeleton} </tex> простого полигона без самопересечений <tex> P </tex>, в котором <tex> n </tex> вершин, как <tex> S(P) </tex>. Тогда | + | Из процесса построения <tex> \mathrm{straight}\ \mathrm{skeleton} </tex> следует, что он является [[Укладка графа на плоскости#defplanar | планарным графом]]. Ранее уже упоминалось, что он также является [[Дерево, эквивалентные определения#tree |деревом]]. Будем обозначать <tex> \mathrm{straight}\ \mathrm{skeleton} </tex> простого полигона без самопересечений <tex> P </tex>, в котором <tex> n </tex> вершин, как <tex> S(P) </tex>. Тогда справедлива следующая лемма: |
{{Лемма | {{Лемма | ||
|id = lemma1 | |id = lemma1 | ||
|about=1 | |about=1 | ||
| − | |statement=<tex> S(P) </tex> является деревом, содержит <tex> n </tex> граней, не более <tex> n - 2 </tex> | + | |statement=<tex> S(P) </tex> является деревом, содержит <tex> n </tex> граней, не более <tex> n - 2 </tex> внутренних вершин и не более <tex> 2 n - 3 </tex> рёбер. |
|proof= | |proof= | ||
| + | |||
| + | [[Файл:skeleton_lemma.png]] | ||
| + | |||
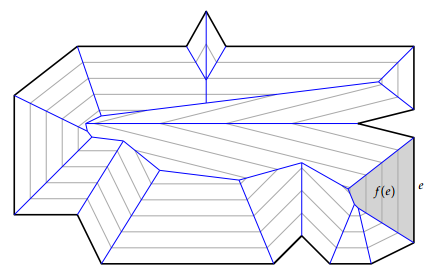
Каждая грань <tex> f(e) </tex> начинает образовываться во время стягивания ребра <tex> e </tex>, и даже если на ребре произошёл <tex> split\ event </tex>, сама грань не могла разделиться. Построение грани <tex> f(e) </tex> завершается, когда ребро <tex> e </tex> полностью стягивается. И это ребро дальше не может появиться снова, поэтому граней в <tex> S(P) </tex> столько, сколько сторон в многоугольнике, то есть ровно <tex> n </tex>. | Каждая грань <tex> f(e) </tex> начинает образовываться во время стягивания ребра <tex> e </tex>, и даже если на ребре произошёл <tex> split\ event </tex>, сама грань не могла разделиться. Построение грани <tex> f(e) </tex> завершается, когда ребро <tex> e </tex> полностью стягивается. И это ребро дальше не может появиться снова, поэтому граней в <tex> S(P) </tex> столько, сколько сторон в многоугольнике, то есть ровно <tex> n </tex>. | ||
| − | То, что <tex> S(P) </tex> является деревом, легко доказывается по индукции. База | + | То, что <tex> S(P) </tex> является деревом, легко доказывается по индукции числа вершин в многоугольнике. |
| + | |||
| + | '''База:''' многоугольник является треугольником, в его <tex> \mathrm{straight}\ \mathrm{skeleton} </tex> будет одна внутренняя вершина {{---}} точка пересечения биссектрис, листьями будут вершины треугольника. Такой граф, очевидно, будет деревом. | ||
| + | |||
| + | '''Переход:''' пусть для всех многоугольников с количеством вершин меньше <tex>k\ S(P)</tex> будет деревом. Рассмотрим самый первый <tex>event</tex> в многоугольнике из <tex>k</tex> вершин. | ||
| + | * Если это <tex>edge\ event</tex>, то появится новая вершина, которую мы соединим с инцидентными ребру вершинами, а также с какой-то вершиной <tex>\mathrm{straight}\ \mathrm{skeleton} </tex> полигона из <tex>k - 1</tex> вершин. Получившийся граф будет деревом. | ||
| + | * Если это <tex>split\ event</tex>, то новая вершина соединяется с одной вершиной исходного полигона и с двумя вершинами <tex>\mathrm{straight}\ \mathrm{skeleton} </tex> для полигонов, в которых меньше <tex> k </tex> вершин. В этом случае также получаем дерево. | ||
| + | |||
Внутренние вершины в <tex> \mathrm{straight}\ \mathrm{skeleton} </tex> имеют [[Основные определения теории графов#def_graph_degree_1 | степень]] не меньше <tex> 3 </tex> {{---}} простой перебор всех случаев <tex> event'</tex>ов (степень будет больше, если в одной вершине совпало несколько событий). Так как <tex> S(P) </tex> имеет <tex>n</tex> листьев, то внутренних вершин будет не больше <tex> n - 2 </tex>, а так как <tex> S(P) </tex> является деревом, то рёбер у него будет не более <tex> 2 n - 3 </tex>. | Внутренние вершины в <tex> \mathrm{straight}\ \mathrm{skeleton} </tex> имеют [[Основные определения теории графов#def_graph_degree_1 | степень]] не меньше <tex> 3 </tex> {{---}} простой перебор всех случаев <tex> event'</tex>ов (степень будет больше, если в одной вершине совпало несколько событий). Так как <tex> S(P) </tex> имеет <tex>n</tex> листьев, то внутренних вершин будет не больше <tex> n - 2 </tex>, а так как <tex> S(P) </tex> является деревом, то рёбер у него будет не более <tex> 2 n - 3 </tex>. | ||
}} | }} | ||
| − | + | Ещё один пример: | |
[[Файл:Skeleton_example1.png|500px]] | [[Файл:Skeleton_example1.png|500px]] | ||
== Алгоритм с изпользованием SLAV == | == Алгоритм с изпользованием SLAV == | ||
| − | Далее будет описан алгоритм, придуманный Petr Felkel, который строит <tex> \mathrm{straight}\ \mathrm{skeleton} </tex> за время <tex> \mathcal{O}( | + | Далее будет описан алгоритм, придуманный Petr Felkel, который строит <tex> \mathrm{straight}\ \mathrm{skeleton} </tex> за время <tex> \mathcal{O}(n^2 \log n)</tex>, где <tex> n </tex> {{---}} общее число вершин в полигоне. В оригинальной статье этому алгоритму даётся асимптотическая оценка <tex> \mathcal{O}(nm + n \log n)</tex>, или просто <tex> \mathcal{O}(n^2)</tex>, где <tex> m </tex> {{---}} число невыпуклых вершин в полигоне. Однако в статье содержатся ошибки, поэтому данная в ней оценка неверна. |
| − | Сначала алгоритм будет рассмотрен на простом случае {{---}} выпуклом многоугольнике, {{---}} а потом на невыпуклом | + | Сначала алгоритм будет рассмотрен на простом случае {{---}} выпуклом многоугольнике, {{---}} а потом на невыпуклом. |
=== Выпуклый полигон === | === Выпуклый полигон === | ||
| − | В случае выпуклого многоугольника возникают только <tex> edge\ event'</tex>ы по определению. | + | В случае выпуклого многоугольника возникают только <tex> edge\ event'</tex>ы по определению. Объяснить алгоритм можно простым образом: найдём точки пересечения биссектрис многоугольника для каждой вершины со всеми соседними вершинами, возьмём такую точку, в которой произойдёт самый первый <tex> edge\ event</tex>, добавим полученную вершину в <tex> \mathrm{straight}\ \mathrm{skeleton} </tex>, соединим её с вершинами ребра, которое исчезло в процессе текущего <tex> edge\ event'</tex>а, а потом перестроим полигон, создав новую вершину и подвинув все остальные вдоль биссектрис на одинаковое расстояние. Будем продолжать этот процесс до тех пор, пока многоугольник не превратится в треугольник. |
| − | Теперь реализуем этот алгоритм более эффективно. Для этого мы будем использовать специальную структуру данных {{---}} <tex> \mathrm{SLAV}</tex> (set of circular lists of active vertices). Эта структура хранит цикл всех вершин для внешней грани, а | + | Теперь реализуем этот алгоритм более эффективно. Для этого мы будем использовать специальную структуру данных {{---}} <tex> \mathrm{SLAV}</tex> (set of circular lists of active vertices). Эта структура хранит цикл всех вершин для внешней грани, а также цикл для каждой дырки многоугольника и для всех многоугольников, возникающих в процессе построения <tex> S(P) </tex>. В данном случае у нас будет просто <tex> \mathrm{LAV}</tex> {{---}} [[Список#Циклический список | циклический список]] всех вершин многоугольника. |
[[Файл:skeleton_lav.jpg]] | [[Файл:skeleton_lav.jpg]] | ||
| − | В таком списке частично найденного <tex> \mathrm{straight}\ \mathrm{skeleton} </tex> вершины имеют указатели на следующую и предыдущую | + | В таком списке частично найденного <tex> \mathrm{straight}\ \mathrm{skeleton} </tex> вершины имеют указатели на следующую и предыдущую вершины в порядке обхода контура, а также указатели на инцидентные рёбра. |
==== Алгоритм для выпуклых полигонов ==== | ==== Алгоритм для выпуклых полигонов ==== | ||
| − | Далее считаем, что полигон представлен рёбрами вдоль движения по контуру | + | Далее считаем, что полигон представлен рёбрами, направленными вдоль движения по контуру против часовой стрелки. |
'''Шаг 1.''' Инициализация: | '''Шаг 1.''' Инициализация: | ||
| − | :<tex>(a)</tex> Поместим все вершины многоугольника <tex> V_1, V_2 \dots V_n </tex> в двусвязный циклический список в порядке обхода вдоль контура. Все вершины в <tex> \mathrm{LAV}</tex> считаются активными | + | :<tex>(a)</tex> Поместим все вершины многоугольника <tex> V_1, V_2 \dots V_n </tex> в двусвязный циклический список в порядке обхода вдоль контура. Все вершины в <tex> \mathrm{LAV}</tex> сейчас считаются активными. |
:<tex>(b)</tex> Для каждой вершины <tex> V_i </tex> в <tex> \mathrm{LAV}</tex> добавим указатели на инцидентные рёбра <tex> e_{i-1} = V_{i-1}V_i</tex> и <tex> e_i = V_i V_{i+1}</tex>, а также найдём луч биссектрисы <tex> b_i </tex>. | :<tex>(b)</tex> Для каждой вершины <tex> V_i </tex> в <tex> \mathrm{LAV}</tex> добавим указатели на инцидентные рёбра <tex> e_{i-1} = V_{i-1}V_i</tex> и <tex> e_i = V_i V_{i+1}</tex>, а также найдём луч биссектрисы <tex> b_i </tex>. | ||
| − | :<tex>(c)</tex> Для каждой вершины <tex> V_i </tex> найдём ближайшее пересечение биссектрисы <tex> b_i </tex> с | + | :<tex>(c)</tex> Для каждой вершины <tex> V_i </tex> найдём ближайшее пересечение биссектрисы <tex> b_i </tex> с биссектрисами <tex> b_{i-1} </tex> и <tex> b_{i+1} </tex>. Если это пересечение существует, то поместим его в [[Двоичная куча | приоритетную очередь]] согласно <tex> L(e_i) </tex> {{---}} расстоянию от точки пересечения до одного из рёбер, инцидентных вершине <tex> V_i </tex>. Для каждой точки пересечения <tex> I_i </tex> будем ещё хранить два указателя на вершины <tex> V_a </tex> и <tex> V_b </tex> {{---}} начала лучей биссектрис, которые пересекаются в точке <tex> I_i </tex>. Эти указатели понадобятся в будущем, когда нужно будет определять соответствующие вершинам рёбра <tex> e_a, e_b </tex> (см. рисунок ниже). |
| − | '''Шаг 2.''' Следующие действия выполняются в цикле, пока приоритетная очередь не | + | '''Шаг 2.''' Следующие действия выполняются в цикле, пока приоритетная очередь не пуста: |
:<tex>(a)</tex> Извлечём точку пересечения <tex> I </tex> из приоритетной очереди. | :<tex>(a)</tex> Извлечём точку пересечения <tex> I </tex> из приоритетной очереди. | ||
| − | :<tex>(b)</tex> Если вершины <tex> V_a </tex> и <tex> V_b </tex>, соответствующие данной точке пересечения помечены как обработанные, то переходим к следующей итерации цикла шага 2. Это означает, что ребро между данными вершинами полностью стянулось (обработанные вершины и стянутые рёбра помечены крестом на рисунке ниже). | + | :<tex>(b)</tex> Если вершины <tex> V_a </tex> и <tex> V_b </tex>, соответствующие данной точке пересечения, помечены как обработанные, то переходим к следующей итерации цикла шага 2. Это означает, что ребро между данными вершинами полностью стянулось (обработанные вершины и стянутые рёбра помечены крестом на рисунке ниже). Эту проверку необходимо делать из-за того, что мы могли поместить в очередь обработанные вершины в момент получения новых <tex>event'</tex>ов. |
| − | :<tex>(c)</tex> Если осталось всего три вершины <tex> V_a, V_b, V_c </tex>, то добавим в <tex> \mathrm{straight}\ \mathrm{skeleton} </tex> рёбра <tex> IV_a, IV_b, IV_c </tex>. В случае выпуклого многоугольника в этом месте можно завершить алгоритм. Но в общем случае нужно будет перейти к началу цикла | + | :<tex>(c)</tex> Если осталось всего три вершины <tex> V_a, V_b, V_c </tex>, то добавим в <tex> \mathrm{straight}\ \mathrm{skeleton} </tex> рёбра <tex> IV_a, IV_b, IV_c </tex>. В случае выпуклого многоугольника в этом месте можно завершить алгоритм. Но в общем случае нужно будет снова перейти к началу цикла. |
:<tex>(d)</tex> Добавим в <tex> \mathrm{straight}\ \mathrm{skeleton} </tex> рёбра <tex> IV_a, IV_b </tex>. | :<tex>(d)</tex> Добавим в <tex> \mathrm{straight}\ \mathrm{skeleton} </tex> рёбра <tex> IV_a, IV_b </tex>. | ||
:<tex>(e)</tex> Теперь необходимо модифицировать <tex> \mathrm{LAV}</tex> (детали на рисунке ниже): | :<tex>(e)</tex> Теперь необходимо модифицировать <tex> \mathrm{LAV}</tex> (детали на рисунке ниже): | ||
::* пометим вершины <tex> V_a </tex> и <tex> V_b </tex> как обработанные (напомню, что они обозначаются крестом на рисунке к данному алгоритму), | ::* пометим вершины <tex> V_a </tex> и <tex> V_b </tex> как обработанные (напомню, что они обозначаются крестом на рисунке к данному алгоритму), | ||
::* создадим новую вершину <tex> V </tex> в точке пересечения <tex> I </tex> (отмечена квадратиком на рисунке), | ::* создадим новую вершину <tex> V </tex> в точке пересечения <tex> I </tex> (отмечена квадратиком на рисунке), | ||
| − | ::* добавим вершину <tex> V </tex> в <tex> \mathrm{LAV}</tex>, то есть между | + | ::* добавим вершину <tex> V </tex> в <tex> \mathrm{LAV}</tex>, то есть между предыдущим к <tex> V_a </tex> и следующим к <tex> V_b </tex> узлами, |
::* добавим вершине <tex> V </tex> указатели на соответствующие рёбра <tex> e_a </tex> и <tex> e_b </tex>. | ::* добавим вершине <tex> V </tex> указатели на соответствующие рёбра <tex> e_a </tex> и <tex> e_b </tex>. | ||
:<tex>(f)</tex> Посчитаем дополнительные величины для вершины <tex> V </tex>: | :<tex>(f)</tex> Посчитаем дополнительные величины для вершины <tex> V </tex>: | ||
::* луч биссектрисы <tex> b </tex> между рёбрами <tex> e_a </tex> и <tex> e_b </tex>, | ::* луч биссектрисы <tex> b </tex> между рёбрами <tex> e_a </tex> и <tex> e_b </tex>, | ||
| − | ::* точки пересечения | + | ::* точки пересечения биссектрисы <tex>b</tex> с биссектрисами вершин, соседних к <tex> V </tex> в <tex> \mathrm{LAV}</tex>, как в шаге <tex> 1c </tex>, |
| − | ::* сохраним ближайшие точки пересечения в приоритетной очереди. | + | ::* сохраним ближайшие точки пересечения в приоритетной очереди. Ключом точки пересечения в приоритетной очереди будет расстояние <tex> L(e_i) </tex> до стянутого ребра <tex> e_i </tex>. |
[[Файл:skeleton_convex_example.png|600px]] | [[Файл:skeleton_convex_example.png|600px]] | ||
| − | |||
| − | |||
В этом случае асимптотика алгоритма составляет <tex> \mathcal{O}(n \log n)</tex>, так как на каждой итерации цикла нам нужно положить константное число элементов в очередь, а итераций цикла не больше <tex> n </tex>. | В этом случае асимптотика алгоритма составляет <tex> \mathcal{O}(n \log n)</tex>, так как на каждой итерации цикла нам нужно положить константное число элементов в очередь, а итераций цикла не больше <tex> n </tex>. | ||
==== Частные случаи ==== | ==== Частные случаи ==== | ||
| − | Частным случаем в алгоритме может быть совпадение нескольких <tex> edge\ event'</tex>ов в одной точке. Эти совпадения добавляются в шагах <tex> 1c </tex> и <tex> 2f </tex>, но могут быть относительно легко обработаны в шаге <tex> 2b </tex>. | + | Частным случаем в алгоритме может быть совпадение нескольких <tex> edge\ event'</tex>ов в одной точке. Эти совпадения добавляются в шагах <tex> 1c </tex> и <tex> 2f </tex>, так как точки пересечения добавляются только в них, но могут быть относительно легко обработаны в шаге <tex> 2b </tex>. Или мы можем считать, что между <tex> edge\ event'</tex>ами в одной точке будут рёбра нулевого веса в полученном <tex> S(P) </tex>, а затем можно просто избавиться от лишних вершин в результирующей структуре. |
| + | |||
| + | Также может случиться, что какие-то рёбра не стянулись в итоге в одну вершину, а слились. Такое возможно, если какие-то стороны полигона были изначально параллельны (этот случай легко увидеть на прямоугольнике, не являющемся квадратом). С этим частным случаем можно разобраться в шаге <tex> 2c </tex>, проверив, не совпала ли одна из трёх вершин с другой. В выпуклом многоугольнике слияние двух рёбер может произойти только один раз (что неправда для невыпуклого многоугольника), поэтому с таким случаем несложно разобраться. | ||
| − | |||
=== Невыпуклый полигон === | === Невыпуклый полигон === | ||
Основной принцип для невыпуклых полигонов такой же. Только с вершиной ещё хранится дополнительный атрибут, обозначающий событие, которое в ней произошло: <tex> edge\ event</tex> или <tex> split\ event</tex>. | Основной принцип для невыпуклых полигонов такой же. Только с вершиной ещё хранится дополнительный атрибут, обозначающий событие, которое в ней произошло: <tex> edge\ event</tex> или <tex> split\ event</tex>. | ||
| + | |||
| + | Если представить процесс стягивания многоугольника, как будто у нас уже построена для него крыша, а мы двигаем вверх некоторую заметающую плоскость, где пересечение крыши и плоскости будет обозначать текущий слой, то можно заметить, что область полигона разбивается на несколько частей. Каждой части будет соответствовать свой <tex> \mathrm{LAV}</tex>, отсюда нам и нужен <tex> \mathrm{SLAV}</tex>. | ||
[[Файл:skeleton_split_event_example.png|400px]] | [[Файл:skeleton_split_event_example.png|400px]] | ||
| − | Наличие невыпуклой вершины может привести (а может и не привести) к разделению внутренней области. Невыпуклая вершина может | + | Наличие невыпуклой вершины может привести (а может и не привести) к разделению внутренней области. Невыпуклая вершина может участвовать в обычном <tex> edge\ event'</tex>е (точка <tex> A </tex> на рисунке выше). <tex> Edge\ event'</tex>ы в случае невыпуклогого многоугольника обрабатываются так же, как и в алгоритме с выпуклым многоугольником. |
Посмотрим теперь, что делать с точкой <tex> B </tex>, в которой возникает <tex> split\ event</tex>. | Посмотрим теперь, что делать с точкой <tex> B </tex>, в которой возникает <tex> split\ event</tex>. | ||
| Строка 109: | Строка 123: | ||
[[Файл:skeleton_b_point_coord.png|500px]] | [[Файл:skeleton_b_point_coord.png|500px]] | ||
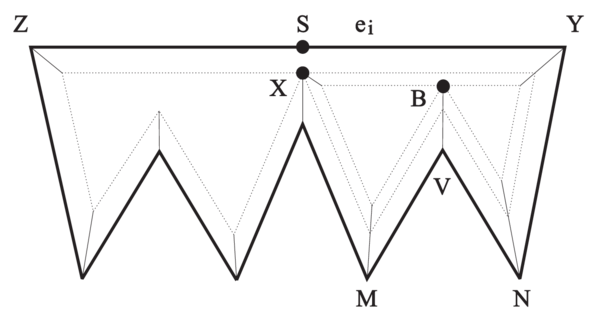
| − | В простейшем случае точка <tex> B </tex> появляется, когда "волновой фронт" распространения движения рёбер от невыпуклой вершины натыкается на встречный фронт противолежащего ребра. В такой момент возникает <tex> split\ event</tex>. Поэтому точка <tex> B </tex> может быть изначально охарактеризована | + | В простейшем случае точка <tex> B </tex> появляется, когда "волновой фронт" распространения движения рёбер от невыпуклой вершины натыкается на встречный фронт противолежащего ребра. В такой момент возникает <tex> split\ event</tex>. Поэтому точка <tex> B </tex> может быть изначально охарактеризована как точка, находящаяся на одном расстоянии от противолежащего ребра и прямых, содержащих рёбра невыпуклой вершины. Задача состоит в том, чтобы найти это самое противолежащее ребро (случай <tex> a) </tex> на рисунке выше). Но как показывает случай <tex> b) </tex>, простой тест на пересечение ребра и биссектрисы невыпуклой вершины (то есть невыпуклая вершина как бы врезается в противолежащее ребро) не может быть использован (в этом случае луч биссектрисы пересекает сразу два ребра, непонятно, с каким из них произойдёт <tex> split\ event</tex>). Поэтому необходимо проверять, что точка <tex> B </tex> лежит в треугольнике, ограниченном противолежащим ребром и биссектрисами <tex> b_i </tex> и <tex> b_{i+1} </tex>, идущими из вершин, инцидентных противолежащему ребру <tex> e_i </tex> (этот треугольник может быть "бесконечным"). |
| − | + | Координаты возможной точки кандидата <tex> B_i </tex> вычисляются следующим образом: это точка пересечения биссектрисы вершины <tex> V </tex> и биссектрисы угла, который образуется в точке пересечения прямой, содержащей одно из рёбер, инцидентных <tex> V </tex>, и прямой, содержащей противолежащее ребро <tex> e_i </tex>. Все такие точки пересечения <tex> B_i </tex> нужно поместить в приоритетную очередь. | |
| − | + | [[Файл:Skeleton_felkel_contr.png]] | |
| − | ''' | + | '''Замечание:''' в оригинальной статье авторы предлагают класть в приоритетную очередь ближайшую из таких точек <tex> B_i </tex>, но тогда алгоритм будет работать некорректно (см. контрпример на рисунке выше). По алгоритму в очередь добавится <tex> split\ event</tex> <tex> p_e </tex> для вершины <tex> v </tex> и ребра <tex> e </tex>, но на самом деле этот <tex> split\ event</tex> произойдёт с ребром <tex>e'</tex> для данной вершины. |
==== Работа с LAV в момент возникновения split event'a ==== | ==== Работа с LAV в момент возникновения split event'a ==== | ||
[[Файл:skeleton_lav_managing.png|600px]] | [[Файл:skeleton_lav_managing.png|600px]] | ||
| − | Когда происходит работа с точкой <tex> B\ split\ event'</tex>а, | + | Когда происходит работа с точкой <tex> B\ split\ event'</tex>а, необходимо разбить соответствующий полигон на две части, что соответствует разделению <tex> \mathrm{LAV} </tex> данного полигона на два списка. И в каждый новый список нужно вставить копию вершины <tex> V </tex>, образующейся в точке пересечения <tex> I </tex>. Обе вершины <tex> V_1 </tex> и <tex> V_2 </tex> указывают на разделяющее ребро <tex> e_i </tex> (см. рисунок выше). |
| − | + | ||
==== Частный случай множественных split event'ов на одном ребре ==== | ==== Частный случай множественных split event'ов на одном ребре ==== | ||
[[Файл:skeleton_collide_edge.jpg]] | [[Файл:skeleton_collide_edge.jpg]] | ||
| − | Уже должно было стать понятно, что алгоритм не строит промежуточного представления <tex> \mathrm{straight}\ \mathrm{skeleton}</tex>, а работает исключительно с рёбрами исходного полигона. Это приводит к ситуации (см. рисунок выше), когда одно ребро является общим для нескольких новых полигонов в промежуточном представлении (то есть одно ребро | + | Уже должно было стать понятно, что алгоритм не строит промежуточного представления <tex> \mathrm{straight}\ \mathrm{skeleton}</tex>, а работает исключительно с рёбрами исходного полигона. Это приводит к ситуации (см. рисунок выше), когда одно ребро является общим для нескольких новых полигонов в промежуточном представлении (то есть одно ребро разбивается несколько раз), образовавшихся после разделения старого полигона. В случае, когда ребро уже разбито, и происходит следующий за ним <tex>event</tex>, необходимо правильно определить концы противолежащего ребра (то есть вершины/узлы, которые активны в текущем уровне конструирования крыши, как например вершины <tex> X </tex> и <tex> Y </tex> на рисунке ниже). |
| − | + | [[Файл:skeleton_multi_edge.png|600px]] | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | Например, в данном случае ребро <tex> SY </tex> является частью ребра <tex> e_i = ZY </tex>, которое стягивается и должно теперь указывать на вершину <tex> X </tex>. Когда произойдёт следующее событие в точке пересечения <tex> B </tex>, нам необходимо правильно указать ребро новой вершине в этой точке в <tex> \mathrm{LAV} </tex>. Реальный конец ребра <tex> e_i </tex> {{---}} точка <tex> Z </tex>, но мы хотим указать на ребро <tex> XY </tex>. Это необходимо для поддержания корректности структуры <tex> \mathrm{SLAV} </tex>. | |
| − | + | Чтобы решить эту проблему, следует хранить <tex>split\ event</tex> как <tex>3</tex> вершины {{---}} невыпуклая вершина и две вершины противолежащего ребра. Дополнительно нужно хранить [[Хеш-таблица | ассоциативный массив]] из пары вершин в ребро для этих вершин. Тогда в момент разделения ребра <tex>ZY</tex> необходимо удалить это ребро из ассоциативного массива и поместить туда два новых ребра <tex>ZX</tex> и <tex>XY</tex>, которые будут ссылаться на исходное ребро <tex> e_i </tex>. | |
| + | |||
| + | Но в очереди могло быть событие по трём вершинам исходного ребра, а после разделения этого ребра уже нет (например, такое может произойти, если с ребром одновременно сталкивается несколько невыпуклых вершин, лежащих на параллельной этому ребру прямой). Посмотрев в ассоциативный массив, можно обнаружить, что такой пары вершин нет. Однако нам нужно всё же получить по ребру требуемую пару вершин. Для этого можно хранить ещё один ассоциативный массив из пар в рёбра, только из него уже не удалять старые пары. Тогда станет возможным получение по паре вершин ребра, а потом по ребру можно будет получить все актуальные пары вершин, соответствующих этому ребру, и добавить <tex>split\ event</tex> с нужной парой вершин. | ||
==== Алгоритм для невыпуклых полигонов ==== | ==== Алгоритм для невыпуклых полигонов ==== | ||
| Строка 141: | Строка 153: | ||
:<tex>(a)</tex> Положим все вершины в <tex> \mathrm{LAV}</tex>, как это делается в алгоритме для выпуклых многоугольников, а потом <tex> \mathrm{LAV}</tex> поместим в <tex> \mathrm{SLAV}</tex>. | :<tex>(a)</tex> Положим все вершины в <tex> \mathrm{LAV}</tex>, как это делается в алгоритме для выпуклых многоугольников, а потом <tex> \mathrm{LAV}</tex> поместим в <tex> \mathrm{SLAV}</tex>. | ||
:<tex>(b)</tex> Найдём биссектрисы как в случае с выпуклым многоугольником. | :<tex>(b)</tex> Найдём биссектрисы как в случае с выпуклым многоугольником. | ||
| − | :<tex>(c)</tex> Для каждой биссектрисы выпуклой вершины найдём ближайшую точку пересечения с биссектрисой соседней вершины, а для невыпуклых вершин найдём также точки пересечения с противолежащими рёбрами (как это описывалось раньше) | + | :<tex>(c)</tex> Для каждой биссектрисы выпуклой вершины найдём ближайшую точку пересечения с биссектрисой соседней вершины, а для невыпуклых вершин найдём также точки пересечения с противолежащими рёбрами (как это описывалось раньше) и положим в приоритетную очередь ближайшую точку пересечения <tex> I </tex>. Будем также с этой точкой хранить её тип {{---}} <tex> edge\ event</tex> или <tex> split\ event</tex>. |
'''Шаг 2.''' Пока очередь не пуста: | '''Шаг 2.''' Пока очередь не пуста: | ||
| − | :<tex>(a)</tex> Извлечём точку пересечения <tex> I </tex> из приоритетной очереди. Если она имеет тип <tex> edge\ event</tex>, то её надо обработать так же, как в шагах <tex> 2b-2f</tex> алгоритма для | + | :<tex>(a)</tex> Извлечём точку пересечения <tex> I </tex> из приоритетной очереди. Если она имеет тип <tex> edge\ event</tex>, то её надо обработать так же, как в шагах <tex> 2b-2f</tex> алгоритма для выпуклых полигонов. Иначе выполнять шаги ниже. |
| − | :<tex>(b)</tex> Если точка пересечения указывает на уже обработанные вершины, то продолжить со следующей итерации цикла шага 2, как в случае с выпуклым полигоном. | + | :<tex>(b)</tex> Если точка пересечения указывает на уже обработанные вершины, то продолжить со следующей итерации цикла шага 2, как в случае с выпуклым полигоном. По этой причине мы не будем обрабатывать лишние <tex> split\ event'</tex>ы, хотя вполне могли их добавить в очередь. |
| − | :<tex>(c)</tex> Нужно сделать примерно то же самое, что и шаге <tex>2c</tex> алгоритма для выпуклых многоугольников. Только на этом цикл не завершается, а продолжается с новой итерации, так как многоугольник мог разделиться на несколько частей, и, возможно, мы обработали лишь один | + | :<tex>(c)</tex> Нужно сделать примерно то же самое, что и шаге <tex>2c</tex> алгоритма для выпуклых многоугольников. Только на этом цикл не завершается, а продолжается с новой итерации, так как многоугольник мог разделиться на несколько частей, и, возможно, мы обработали лишь один подполигон и не последний. |
:<tex>(d)</tex> Добавим в <tex> \mathrm{straight}\ \mathrm{skeleton} </tex> ребро <tex> IV </tex>, где точка <tex> I </tex> указывает на вершину <tex> V </tex>. Для <tex> split\ event'</tex>ов точки пересечения указывают ровно на одну вершину в <tex> \mathrm{SLAV}</tex>. | :<tex>(d)</tex> Добавим в <tex> \mathrm{straight}\ \mathrm{skeleton} </tex> ребро <tex> IV </tex>, где точка <tex> I </tex> указывает на вершину <tex> V </tex>. Для <tex> split\ event'</tex>ов точки пересечения указывают ровно на одну вершину в <tex> \mathrm{SLAV}</tex>. | ||
:<tex>(e)</tex> Модифицируем теперь <tex> \mathrm{SLAV}</tex>: | :<tex>(e)</tex> Модифицируем теперь <tex> \mathrm{SLAV}</tex>: | ||
| Строка 151: | Строка 163: | ||
::* создадим две новые вершины <tex> V_1 </tex> и <tex> V_2 </tex> с одинаковыми координатами точки пересечения <tex> I </tex>, | ::* создадим две новые вершины <tex> V_1 </tex> и <tex> V_2 </tex> с одинаковыми координатами точки пересечения <tex> I </tex>, | ||
::* найдём для каждой вершины <tex> V_1 </tex> и <tex> V_2 </tex> противолежащее ребро в своём подпалигоне, | ::* найдём для каждой вершины <tex> V_1 </tex> и <tex> V_2 </tex> противолежащее ребро в своём подпалигоне, | ||
| − | ::* разделим <tex> \mathrm{LAV}</tex> с вершиной <tex> V </tex> на две части (как показано на рисунке выше), вставим в части вершины <tex> V_1 </tex> и <tex> V_2 </tex>, а затем обе части добавим в <tex> \mathrm{SLAV}</tex>. Вершина <tex> V_1 </tex> будет следующей для предыдующего к <tex> V </tex> | + | ::* разделим <tex> \mathrm{LAV}</tex> с вершиной <tex> V </tex> на две части (как показано на рисунке выше), вставим в части вершины <tex> V_1 </tex> и <tex> V_2 </tex>, а затем обе части добавим в <tex> \mathrm{SLAV}</tex>. Вершина <tex> V_1 </tex> будет следующей для предыдующего к <tex> V </tex> узла в <tex> \mathrm{LAV}</tex> и предыдущей для конца противолежащего ребра. Аналогично для вершины <tex> V_2 </tex>, |
| − | ::* | + | ::* удалим из ассоциативного массива пару вершин ребра <tex> e_i </tex> и поместим две новых пары, в одной из которых будет вершина <tex> V_1 </tex> и конец ребра <tex> e_i </tex>, а в другом {{---}} начало <tex> e_i </tex> и вершина <tex> V_2 </tex>, |
| + | ::* добавим указатели на соответствующие рёбра вершинам <tex> V_1 </tex> и <tex> V_2 </tex>. | ||
:<tex>(f)</tex> Для обеих вершин <tex> V_1 </tex> и <tex> V_2 </tex>: | :<tex>(f)</tex> Для обеих вершин <tex> V_1 </tex> и <tex> V_2 </tex>: | ||
| − | ::* найдём биссектрисы между рёбрами, на которые эти вершины | + | ::* найдём биссектрисы между рёбрами, на которые эти вершины указывают в шаге <tex>2e</tex>, |
| − | ::* найдём | + | ::* найдём все события точек пересечения как в шаге <tex> 1c </tex> (тут могут получиться события обоих типов), |
| − | ::* сохраним | + | ::* сохраним точки пересечения, отвечающие найденным событиям, в приоритетной очереди. |
| − | Обработка | + | Обработка <tex> edge\ event'</tex>ов выполняется с такой же асимптотикой, как и в алгоритме для выпуклых полигонов. Но из-за того, что в очередь кладутся всевозможные точки, в которых произошли <tex> split\ event'</tex>ы, в ней может оказаться <tex>\mathcal{O}(n^2)</tex> элементов. Хотя обработка <tex> split\ event'</tex>а может занять линейное время от числа вершин (если новая вершина в точке пересечения осталась невыпуклой), это произойдёт только для <tex> split\ event'</tex>ов, которые создают новые вершины <tex> S(P) </tex>, а их <tex>\mathcal{O}(n)</tex> по доказанной [[#lemma1 | лемме]]. Остальные <tex> split\ event'</tex>ы обработаются за <tex>\mathcal{O}(1)</tex> в шаге <tex> 2b </tex>, поэтому итоговая асимптотика составит <tex>\mathcal{O}(n^2 \log n)</tex>. |
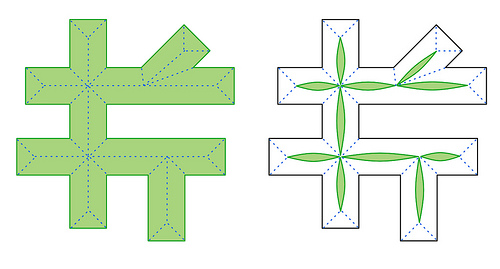
| − | ==== Случай полигонов с | + | ==== Случай полигонов с дырками ==== |
| − | Данный алгоритм может работать и с многоугольниками, содержащими | + | Данный алгоритм может работать и с многоугольниками, содержащими дырки, если они ориентированы по часовой стрелке, чтобы внутренняя область многоугольника лежала слева от рёбер. И в самом начале алгоритма каждый замкнутый контур помещается в свой <tex> \mathrm{LAV} </tex> в множестве <tex> \mathrm{SLAV} </tex>. |
[[Файл:skeleton_hole_example.png|500px]] | [[Файл:skeleton_hole_example.png|500px]] | ||
| Строка 169: | Строка 182: | ||
==== Особенности реализации и другие частные случаи ==== | ==== Особенности реализации и другие частные случаи ==== | ||
| − | {{ | + | Приведённый здесь алгоритм плох тем (кроме того, что медленно работает), что является довольно общим и не рассматривает возникающие на практике сложные частные случаи. Он будет работать на произвольных случайных полигонах, в которых возникают только простые события (картинка ниже) {{---}} в точке <tex> a </tex> произошёл <tex> edge\ event </tex>, в точке <tex> b </tex> {{---}} <tex> split\ event </tex>, а точки <tex> c </tex> и <tex> d </tex> уже внутри треугольников, и с ними разобраться просто. |
| − | {{ | + | |
| + | [[Файл:skeleton_simple_event_example.jpg]] | ||
| + | |||
| + | Но на практике может возникнуть что-то менее тривиальное (картинка ниже): совпадение многих <tex> edge\ event'</tex>ов в одной точке, многих <tex> split\ event'</tex>ов, или даже в одной точке могут одновременно произойти события двух типов, а также многократное наложение параллельных рёбер друг на друга. | ||
| + | |||
| + | [[Файл:skeleton_complex_event_example.jpg]] | ||
| + | |||
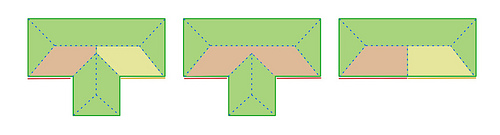
| + | ===== Параллельные противоположные рёбра ===== | ||
| + | С точками <tex> c </tex> и <tex> d </tex> необходимо разбираться следующим образом: как только параллельные рёбра становятся соседними перед событием, нужно проверить, что после произошедшего события они соединятся потом в одно ребро. Если в <tex> \mathrm{LAV} </tex> осталось только два параллельных ребра, то мы удаляем их из <tex> \mathrm{SLAV} </tex>. | ||
| + | |||
| + | Ещё примеры не для слабонервных. | ||
| + | |||
| + | [[Файл:skeleton_parallel_edges.jpg|300px]] | ||
| + | |||
| + | [[Файл:skeleton_more_complex_event_example3.jpg]] | ||
| + | |||
| + | ===== Параллельные "соседние" рёбра ===== | ||
| + | [[Файл:skeleton_pce_event_example.jpg]] | ||
| + | |||
| + | Другой интересный случай возникает, когда несоседние параллельные рёбра становятся соседними после исчезания рёбер между ними. Такая проблема называется <tex> \mathrm{PCE} </tex> (''parallel consecutive edge problem''). В таком случае можно поступать по-разному. | ||
| + | * На левом рисунке используется <tex>separate\ rule</tex> {{---}} согласно этому правилу два ребра рассматриваются отдельно. Тогда верно утверждение, что каждому ребру соответствует ровно одна грань. И в этом случае можно считать, что новая вершина на стыке двух рёбер движется перпендикулярно рёбрам. | ||
| + | * На среднем рисунке используется <tex>merge\ rule</tex> {{---}} рёбра в таком случае объединяются в одно новое ребро. | ||
| + | |||
| + | Отличить этот случай от предыдущего можно, посмотрев на ориентацию двух рёбер. Если они направлены в одну сторону, то это <tex> \mathrm{PCE} </tex>, если в противоположную, то разбираемся как в предыдущем случае. | ||
| + | |||
| + | ===== Множественные события в одной точке ===== | ||
| + | Первая проблема, возникающая в этом случае {{---}} точное определение того, что несколько событий произошли в одной точке. Для определения совпадения нескольких событий в одной точке можно поступать приближённо: вводить с каждой точкой <tex>\varepsilon</tex>-окрестность и смотреть, не попали ли другие точки в эту окрестность, или использовать более точную арифметику<ref>[http://www.mpfr.org/ The GNU MPFR Library]</ref>. В данном случае недостаточно использовать [[Интервальная арифметика | интервальную арифметику]] или даже рациональную арифметику. Потому что даже если координаты точек задаются абсолютно точно, то для подсчёта радиуса вписанной окружности необходимо уметь извлекать корни (напомним, что радиус вписанной окружности равен площади, поделённой на полупериметр, а длины сторон треугольников {{---}} корни из [[Гильбертовы пространства | скалярного произведения]] векторов разницы точек на самих себя). | ||
| + | |||
| + | Чтобы научиться разбираться с такими случаями в алгоритме, когда мы уже поняли, что в одной точке будет несколько событий, введём понятие '''обобщённого события пересечения''' (англ. ''GIE'', ''generalized intersection event''). | ||
| + | |||
| + | [[Файл:skeleton_chain1.jpg]] | ||
| + | |||
| + | Для начала введём понятие цепочек рёбер, которые вовлечены в событие {{---}} такие рёбра, которые сталкиваются в данном событии. Эти цепи упорядочим согласно направлению рёбер (см. рисунок выше). | ||
| + | |||
| + | [[Файл:skeleton_chain2.jpg]] | ||
| + | |||
| + | Мы можем также упорядочить сами цепи вокруг точки события, объединив эти цепи в один циклический список. Следовательно, событие получается как бы окружено списком рёбер, которые участвуют в нём, при этом никакие другие рёбра не участвуют. Можно заметить (рисунки <tex> c,\ d,\ e</tex> выше), что соседние рёбра в списке из изначально разных цепей становятся потом соседними в <tex>\mathrm{LAV}</tex>. | ||
| + | |||
| + | Алгоритм обработки GIE следующий: | ||
| + | * '''Шаг внутри цепи:''' в каждой цепи удаляем внутренние рёбра (кроме первого и последнего) {{---}} это соответствует тому, что исчезает несколько рёбер, участвующих в одном <tex>edge\ event'</tex>е. После этого шага остаются цепи только длин <tex>1</tex> или <tex>2</tex>. | ||
| + | * '''Шаг цепи из одного звена:''' цепи длины <tex>1</tex> разбиваются в точке события (это соответствует простому <tex>split\ event'</tex>у). Теперь все цепи имеют длину ровно <tex>2</tex>. | ||
| + | * '''Шаг межцепной:''' объединяем соседние цепи (соответствующие одному событию) в циклический список, соединяя конец одной цепи с началом следующей и так далее. Поэтому каждая цепь разбивается в середине, и образуются новые списки длины <tex>2</tex>. | ||
| + | * '''Шаг циклы из двух рёбер:''' списки <tex>\mathrm{LAV}</tex> длины <tex>2</tex> состоящие из двух параллельных рёбер, то есть ограничивающие полигон нулевой площади, удаляются из <tex>\mathrm{SLAV}</tex>. | ||
| + | * '''Шаг PCE:''' разбираемся с <tex> \mathrm{PCE} </tex> согласно принятому нами правилу решения {{---}} правилу слияния или правилу разделения. | ||
| + | |||
| + | В реализации это будет выглядеть следующим образом: можно посмотреть, что сейчас лежит в голове приоритетной очереди, и доставать события, пока они происходят в одной точке, а потом разбить эти события на цепочки и выполнять шаги из алгоритма выше. | ||
| − | == | + | ==== Открытые реализации ==== |
| − | + | Приведённый здесь алгоритм был реализован Fernando Cacciola<ref>[https://www.cgal.org/UserWorkshop/2004/straight_skeleton.pdf Fernando Cacciola, "A CGAL implementation of the Straight Skeleton of a Simple 2D Polygon with Holes "]</ref>, который исправил все ошибки в статье P. Felkel. И этот алгоритм используется в открытой библиотеке вычислительной геометрии CGAL<ref>[http://doc.cgal.org/latest/Straight_skeleton_2/index.html CGAL 4.5 {{---}} 2D Straight Skeleton and Polygon Offsetting]</ref>. Более того, он является одной из немногих открытых реализаций построения <tex> \mathrm{straight}\ \mathrm{skeleton} </tex>. Но данный алгоритм достаточно медленный для решения практических задач. В реальной жизни используют его модификации или более сложные алгоритмы. | |
| − | |||
== Другие алгоритмы == | == Другие алгоритмы == | ||
Существует простой в понимании и реализации алгоритм для построения <tex> \mathrm{straigt}\ \mathrm{skeleton}</tex> на основе [[Триангуляция полигонов (ушная + монотонная)|триангуляции]], который работает за время <tex> \mathcal{O}(n^3 \log n)</tex><ref>[http://www.sthu.org/research/publications/files/eurocg2010-slides.pdf Stefan Huber, Martin Held, "Straight Skeletons and their Relation to Triangulations"]</ref>. Aichholzer смог обобщить этот алгоритм для построения <tex> \mathrm{straigt}\ \mathrm{skeleton}</tex> произвольного планарного графа<ref>[http://citeseerx.ist.psu.edu/viewdoc/summary?doi=10.1.1.33.2586 Oswin Aichholzer, Franz Aurenhammera, "Straight Skeletons for General Polygonal Figures in the Plane"]</ref>. Также автором в его оригинальной статье был представлен алгоритм построения данной структуры, базирующийся на понятии '''волнового фронта''' (англ. ''wavefront''). Этот алгоритм может быть реализован за время <tex> \mathcal{O}(n^3)</tex> с использованием <tex> \mathcal{O}(n)</tex> памяти либо с использованием [[Двоичная куча | приоритетной очереди]] за время <tex> \mathcal{O}(n^2 \log n)</tex> и <tex> \mathcal{O}(n^2)</tex> памяти<ref>[http://www.jucs.org/jucs_1_12/a_novel_type_of/Aichholzer_O.pdf Oswin Aichholzer, Franz Aurenhammera, "A Novel Type of Skeleton for Polygons"]</ref>. Известен алгоритм построения <tex> \mathrm{straight}\ \mathrm{skeleton} </tex> для [[Триангуляция полигонов (ушная + монотонная)#def_monotone_polygon|монотонных полигонов]] за время <tex> \mathcal{O}(n \log n)</tex> с использованием <tex> \mathcal{O}(n)</tex> памяти<ref>[http://www.cs.bgu.ac.il/~eurocg14/papers/paper_9.pdf Therese Biedl, Martin Held, Stefan Huber, Dominik Kaaser, Peter Palfrader, "Straight Skeletons of Monotone Polygons"]</ref>. | Существует простой в понимании и реализации алгоритм для построения <tex> \mathrm{straigt}\ \mathrm{skeleton}</tex> на основе [[Триангуляция полигонов (ушная + монотонная)|триангуляции]], который работает за время <tex> \mathcal{O}(n^3 \log n)</tex><ref>[http://www.sthu.org/research/publications/files/eurocg2010-slides.pdf Stefan Huber, Martin Held, "Straight Skeletons and their Relation to Triangulations"]</ref>. Aichholzer смог обобщить этот алгоритм для построения <tex> \mathrm{straigt}\ \mathrm{skeleton}</tex> произвольного планарного графа<ref>[http://citeseerx.ist.psu.edu/viewdoc/summary?doi=10.1.1.33.2586 Oswin Aichholzer, Franz Aurenhammera, "Straight Skeletons for General Polygonal Figures in the Plane"]</ref>. Также автором в его оригинальной статье был представлен алгоритм построения данной структуры, базирующийся на понятии '''волнового фронта''' (англ. ''wavefront''). Этот алгоритм может быть реализован за время <tex> \mathcal{O}(n^3)</tex> с использованием <tex> \mathcal{O}(n)</tex> памяти либо с использованием [[Двоичная куча | приоритетной очереди]] за время <tex> \mathcal{O}(n^2 \log n)</tex> и <tex> \mathcal{O}(n^2)</tex> памяти<ref>[http://www.jucs.org/jucs_1_12/a_novel_type_of/Aichholzer_O.pdf Oswin Aichholzer, Franz Aurenhammera, "A Novel Type of Skeleton for Polygons"]</ref>. Известен алгоритм построения <tex> \mathrm{straight}\ \mathrm{skeleton} </tex> для [[Триангуляция полигонов (ушная + монотонная)#def_monotone_polygon|монотонных полигонов]] за время <tex> \mathcal{O}(n \log n)</tex> с использованием <tex> \mathcal{O}(n)</tex> памяти<ref>[http://www.cs.bgu.ac.il/~eurocg14/papers/paper_9.pdf Therese Biedl, Martin Held, Stefan Huber, Dominik Kaaser, Peter Palfrader, "Straight Skeletons of Monotone Polygons"]</ref>. | ||
| − | + | Также существует более эффективный алгоритм на основе мотографов, который придумали Stefan Huber и Martin Held. Их реализация называется <tex>\mathrm{STALGO}</tex>, и она доступна на их сайте<ref>[https://www.sthu.org/code/stalgo/ STALGO {{---}} an industrial-strength C++ software package for computing straight skeletons and mitered offset-curves]</ref>. | |
== См. также == | == См. также == | ||
| Строка 193: | Строка 250: | ||
* [http://www.dma.fi.upm.es/mabellanas/tfcs/skeleton/html/documentacion/straight%20skeletons%20implementation.pdf Petr Felkel, Stepan Obdrazalek, "Straight Skeleton Implementation"] | * [http://www.dma.fi.upm.es/mabellanas/tfcs/skeleton/html/documentacion/straight%20skeletons%20implementation.pdf Petr Felkel, Stepan Obdrazalek, "Straight Skeleton Implementation"] | ||
* [http://twak.blogspot.ru/2009/05/engineering-weighted-straight-skeleton.html Engineering a weighted straight skeleton algorithm] | * [http://twak.blogspot.ru/2009/05/engineering-weighted-straight-skeleton.html Engineering a weighted straight skeleton algorithm] | ||
| − | * [https://code.google.com/p/campskeleton/ Визуализатор алгоритма | + | * [https://code.google.com/p/campskeleton/ Визуализатор алгоритма] |
| − | |||
[[Категория: Вычислительная геометрия]] | [[Категория: Вычислительная геометрия]] | ||
| − | [[Категория: | + | [[Категория: Триангуляция Делоне и диаграмма Вороного]] |
[[Категория: Структуры данных]] | [[Категория: Структуры данных]] | ||
Текущая версия на 19:42, 4 сентября 2022
Структура была придумана Oswin Aichholzer. Она используется в различных практических задачах (проектирование крыш для зданий), для доказательства некоторых теорем[1], в обработке изображений — эрозия и дилатация, но самое главное — можно оффсетить полигоны и упрощать их.
Содержание
- 1 Топологические свойства
- 2 Свойства Straight skeleton
- 3 Алгоритм с изпользованием SLAV
- 3.1 Выпуклый полигон
- 3.2 Невыпуклый полигон
- 3.2.1 Нахождение координат точки B
- 3.2.2 Работа с LAV в момент возникновения split event'a
- 3.2.3 Частный случай множественных split event'ов на одном ребре
- 3.2.4 Алгоритм для невыпуклых полигонов
- 3.2.5 Случай полигонов с дырками
- 3.2.6 Особенности реализации и другие частные случаи
- 3.2.7 Открытые реализации
- 4 Другие алгоритмы
- 5 См. также
- 6 Примечания
- 7 Источники информации
Топологические свойства
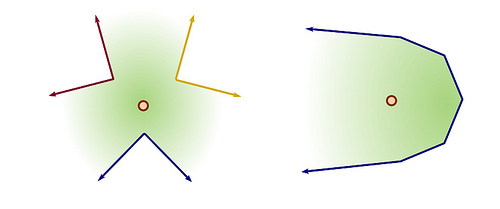
Далее будет дано процедурное определение .
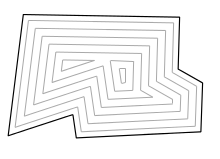
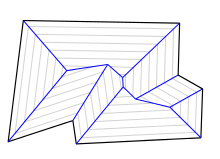
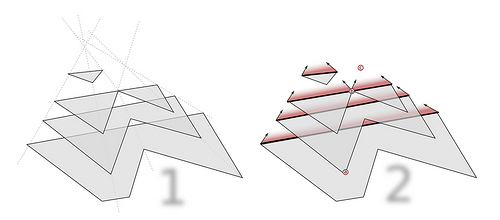
Можно представить, будто все стороны многоугольника параллельно двигаются внутрь с одинаковой постоянной скоростью, то есть многоугольник как бы сжимается внутрь. Тогда вершины будут двигаться вдоль биссектрис внутренних углов , а точки пересечения биссектрис будут являться точками, в которых рёбра полностью сократятся (выродятся в точку). В каждый момент времени от начала движения рёбер получается слоистая структура (рис 1.). На рис. 2 синим цветом выделен — множество отрезков, образованных точками пересечения при движении сторон полигона. Эта структура напоминает построение крыши для дома (рис. 3), и, в самом деле, скелетон применяется для решения подобных задач: по стенам здания необходимо спроектировать его крышу.
Процесс стягивания многоугольника продолжается до тех пор, пока все рёбра не сожмутся в точку, то есть пока меняется число вершин в стянутом многоугольнике, и таким образом появляются новые вершины . Существуют два типа изменений, в ходе которых они образуются:
- — данное изменение происходит, когда сторона многоугольника полностью стягивается, делая соседние стороны инцидентными.
- — происходит, когда ребро разбивается на два новых ребра, исходящих из точки преломления старого. Такое событие происходит на биссектрисе вогнутой вершины многоугольника. И тогда стягиваемая многоугольником область может разбиваться на две непересекающиеся многоугольные области.
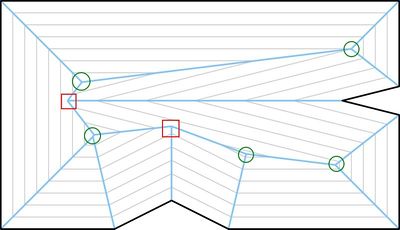
На рисунке ы отмечены зелёными окружностями, а ы — красными квадратами.
Таким образом, можно предъявить соответствие между элементами и происходящими событиями:
- внутренние вершины — ы,
- листья — вершины исходного многоугольника,
- грани — области многоугольника, заметаемые сторонами многоугольника в процессе стягивания,
- дуги — соединяют либо две внутренние вершины, либо внутреннюю вершину с листом.
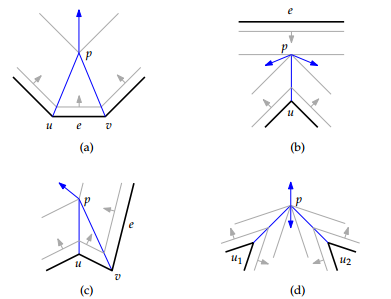
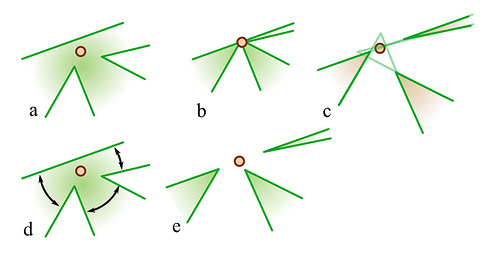
Стоит также отметить, что в общем случае ы могут быть нетривиальными. На рисунке ниже в случае в вершине совпали из вершины и ребра и ребра , а в случае совпали два а вершин и . Случаи и — простые и ы.
Задача построения такого является частным случаем задачи построения , где каждому ребру можно задавать вес, то есть скорость движения ребра. И эта скорость может быть даже отрицательной. Но задача построения является в общем случае неопределённой. В процессе её решения возникают неоднозначности[2]. Задача является более сложной, и здесь рассматриваться не будет.
Алгоритм построения можно модифицировать, чтобы волновой фронт шёл от полигона. То есть сначала можно построить , тем самым упростив структуру полигона и сделав его более "гладким", а затем распространить волну в обратную сторону.
Свойства Straight skeleton
Из процесса построения следует, что он является планарным графом. Ранее уже упоминалось, что он также является деревом. Будем обозначать простого полигона без самопересечений , в котором вершин, как . Тогда справедлива следующая лемма:
| Лемма (1): |
является деревом, содержит граней, не более внутренних вершин и не более рёбер. |
| Доказательство: |
|
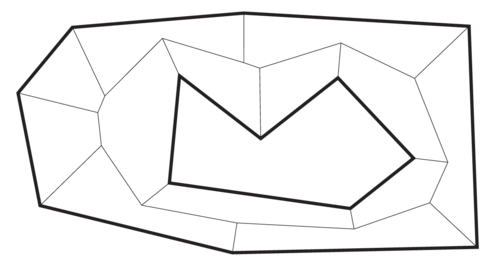
Каждая грань начинает образовываться во время стягивания ребра , и даже если на ребре произошёл , сама грань не могла разделиться. Построение грани завершается, когда ребро полностью стягивается. И это ребро дальше не может появиться снова, поэтому граней в столько, сколько сторон в многоугольнике, то есть ровно . То, что является деревом, легко доказывается по индукции числа вершин в многоугольнике. База: многоугольник является треугольником, в его будет одна внутренняя вершина — точка пересечения биссектрис, листьями будут вершины треугольника. Такой граф, очевидно, будет деревом. Переход: пусть для всех многоугольников с количеством вершин меньше будет деревом. Рассмотрим самый первый в многоугольнике из вершин.
|
Ещё один пример:
Алгоритм с изпользованием SLAV
Далее будет описан алгоритм, придуманный Petr Felkel, который строит за время , где — общее число вершин в полигоне. В оригинальной статье этому алгоритму даётся асимптотическая оценка , или просто , где — число невыпуклых вершин в полигоне. Однако в статье содержатся ошибки, поэтому данная в ней оценка неверна.
Сначала алгоритм будет рассмотрен на простом случае — выпуклом многоугольнике, — а потом на невыпуклом.
Выпуклый полигон
В случае выпуклого многоугольника возникают только ы по определению. Объяснить алгоритм можно простым образом: найдём точки пересечения биссектрис многоугольника для каждой вершины со всеми соседними вершинами, возьмём такую точку, в которой произойдёт самый первый , добавим полученную вершину в , соединим её с вершинами ребра, которое исчезло в процессе текущего а, а потом перестроим полигон, создав новую вершину и подвинув все остальные вдоль биссектрис на одинаковое расстояние. Будем продолжать этот процесс до тех пор, пока многоугольник не превратится в треугольник.
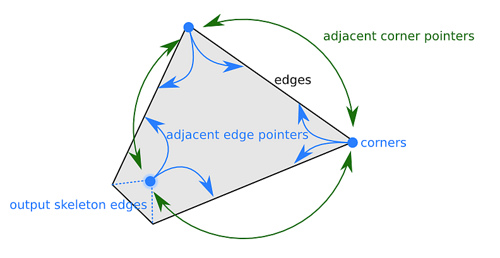
Теперь реализуем этот алгоритм более эффективно. Для этого мы будем использовать специальную структуру данных — (set of circular lists of active vertices). Эта структура хранит цикл всех вершин для внешней грани, а также цикл для каждой дырки многоугольника и для всех многоугольников, возникающих в процессе построения . В данном случае у нас будет просто — циклический список всех вершин многоугольника.
В таком списке частично найденного вершины имеют указатели на следующую и предыдущую вершины в порядке обхода контура, а также указатели на инцидентные рёбра.
Алгоритм для выпуклых полигонов
Далее считаем, что полигон представлен рёбрами, направленными вдоль движения по контуру против часовой стрелки.
Шаг 1. Инициализация:
- Поместим все вершины многоугольника в двусвязный циклический список в порядке обхода вдоль контура. Все вершины в сейчас считаются активными.
- Для каждой вершины в добавим указатели на инцидентные рёбра и , а также найдём луч биссектрисы .
- Для каждой вершины найдём ближайшее пересечение биссектрисы с биссектрисами и . Если это пересечение существует, то поместим его в приоритетную очередь согласно — расстоянию от точки пересечения до одного из рёбер, инцидентных вершине . Для каждой точки пересечения будем ещё хранить два указателя на вершины и — начала лучей биссектрис, которые пересекаются в точке . Эти указатели понадобятся в будущем, когда нужно будет определять соответствующие вершинам рёбра (см. рисунок ниже).
Шаг 2. Следующие действия выполняются в цикле, пока приоритетная очередь не пуста:
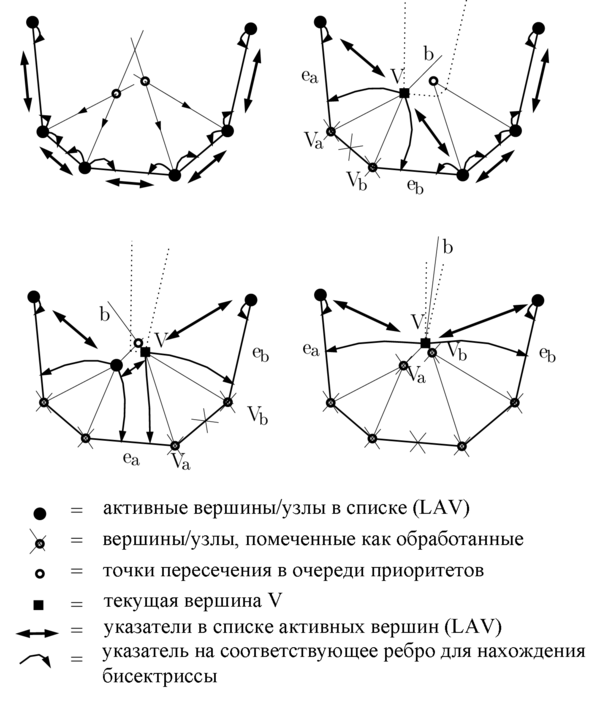
- Извлечём точку пересечения из приоритетной очереди.
- Если вершины и , соответствующие данной точке пересечения, помечены как обработанные, то переходим к следующей итерации цикла шага 2. Это означает, что ребро между данными вершинами полностью стянулось (обработанные вершины и стянутые рёбра помечены крестом на рисунке ниже). Эту проверку необходимо делать из-за того, что мы могли поместить в очередь обработанные вершины в момент получения новых ов.
- Если осталось всего три вершины , то добавим в рёбра . В случае выпуклого многоугольника в этом месте можно завершить алгоритм. Но в общем случае нужно будет снова перейти к началу цикла.
- Добавим в рёбра .
- Теперь необходимо модифицировать (детали на рисунке ниже):
- пометим вершины и как обработанные (напомню, что они обозначаются крестом на рисунке к данному алгоритму),
- создадим новую вершину в точке пересечения (отмечена квадратиком на рисунке),
- добавим вершину в , то есть между предыдущим к и следующим к узлами,
- добавим вершине указатели на соответствующие рёбра и .
- Посчитаем дополнительные величины для вершины :
- луч биссектрисы между рёбрами и ,
- точки пересечения биссектрисы с биссектрисами вершин, соседних к в , как в шаге ,
- сохраним ближайшие точки пересечения в приоритетной очереди. Ключом точки пересечения в приоритетной очереди будет расстояние до стянутого ребра .
В этом случае асимптотика алгоритма составляет , так как на каждой итерации цикла нам нужно положить константное число элементов в очередь, а итераций цикла не больше .
Частные случаи
Частным случаем в алгоритме может быть совпадение нескольких ов в одной точке. Эти совпадения добавляются в шагах и , так как точки пересечения добавляются только в них, но могут быть относительно легко обработаны в шаге . Или мы можем считать, что между ами в одной точке будут рёбра нулевого веса в полученном , а затем можно просто избавиться от лишних вершин в результирующей структуре.
Также может случиться, что какие-то рёбра не стянулись в итоге в одну вершину, а слились. Такое возможно, если какие-то стороны полигона были изначально параллельны (этот случай легко увидеть на прямоугольнике, не являющемся квадратом). С этим частным случаем можно разобраться в шаге , проверив, не совпала ли одна из трёх вершин с другой. В выпуклом многоугольнике слияние двух рёбер может произойти только один раз (что неправда для невыпуклого многоугольника), поэтому с таким случаем несложно разобраться.
Невыпуклый полигон
Основной принцип для невыпуклых полигонов такой же. Только с вершиной ещё хранится дополнительный атрибут, обозначающий событие, которое в ней произошло: или .
Если представить процесс стягивания многоугольника, как будто у нас уже построена для него крыша, а мы двигаем вверх некоторую заметающую плоскость, где пересечение крыши и плоскости будет обозначать текущий слой, то можно заметить, что область полигона разбивается на несколько частей. Каждой части будет соответствовать свой , отсюда нам и нужен .
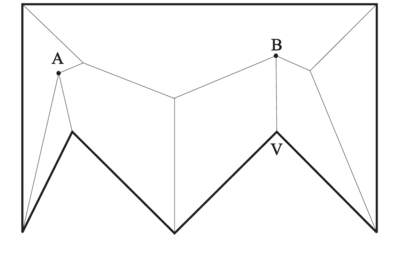
Наличие невыпуклой вершины может привести (а может и не привести) к разделению внутренней области. Невыпуклая вершина может участвовать в обычном е (точка на рисунке выше). ы в случае невыпуклогого многоугольника обрабатываются так же, как и в алгоритме с выпуклым многоугольником.
Посмотрим теперь, что делать с точкой , в которой возникает .
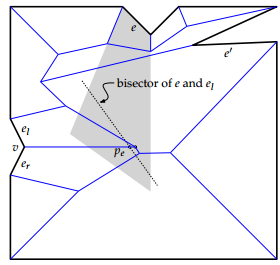
Нахождение координат точки B
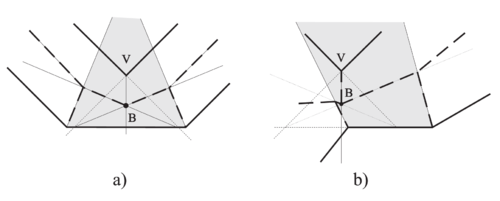
В простейшем случае точка появляется, когда "волновой фронт" распространения движения рёбер от невыпуклой вершины натыкается на встречный фронт противолежащего ребра. В такой момент возникает . Поэтому точка может быть изначально охарактеризована как точка, находящаяся на одном расстоянии от противолежащего ребра и прямых, содержащих рёбра невыпуклой вершины. Задача состоит в том, чтобы найти это самое противолежащее ребро (случай на рисунке выше). Но как показывает случай , простой тест на пересечение ребра и биссектрисы невыпуклой вершины (то есть невыпуклая вершина как бы врезается в противолежащее ребро) не может быть использован (в этом случае луч биссектрисы пересекает сразу два ребра, непонятно, с каким из них произойдёт ). Поэтому необходимо проверять, что точка лежит в треугольнике, ограниченном противолежащим ребром и биссектрисами и , идущими из вершин, инцидентных противолежащему ребру (этот треугольник может быть "бесконечным").
Координаты возможной точки кандидата вычисляются следующим образом: это точка пересечения биссектрисы вершины и биссектрисы угла, который образуется в точке пересечения прямой, содержащей одно из рёбер, инцидентных , и прямой, содержащей противолежащее ребро . Все такие точки пересечения нужно поместить в приоритетную очередь.
Замечание: в оригинальной статье авторы предлагают класть в приоритетную очередь ближайшую из таких точек , но тогда алгоритм будет работать некорректно (см. контрпример на рисунке выше). По алгоритму в очередь добавится для вершины и ребра , но на самом деле этот произойдёт с ребром для данной вершины.
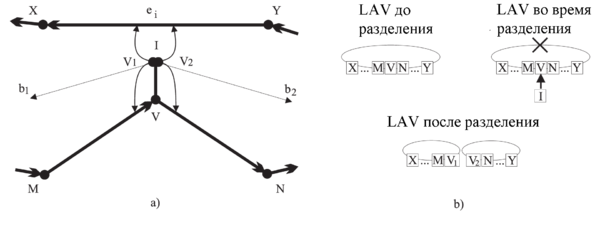
Работа с LAV в момент возникновения split event'a
Когда происходит работа с точкой а, необходимо разбить соответствующий полигон на две части, что соответствует разделению данного полигона на два списка. И в каждый новый список нужно вставить копию вершины , образующейся в точке пересечения . Обе вершины и указывают на разделяющее ребро (см. рисунок выше).
Частный случай множественных split event'ов на одном ребре
Уже должно было стать понятно, что алгоритм не строит промежуточного представления , а работает исключительно с рёбрами исходного полигона. Это приводит к ситуации (см. рисунок выше), когда одно ребро является общим для нескольких новых полигонов в промежуточном представлении (то есть одно ребро разбивается несколько раз), образовавшихся после разделения старого полигона. В случае, когда ребро уже разбито, и происходит следующий за ним , необходимо правильно определить концы противолежащего ребра (то есть вершины/узлы, которые активны в текущем уровне конструирования крыши, как например вершины и на рисунке ниже).
Например, в данном случае ребро является частью ребра , которое стягивается и должно теперь указывать на вершину . Когда произойдёт следующее событие в точке пересечения , нам необходимо правильно указать ребро новой вершине в этой точке в . Реальный конец ребра — точка , но мы хотим указать на ребро . Это необходимо для поддержания корректности структуры .
Чтобы решить эту проблему, следует хранить как вершины — невыпуклая вершина и две вершины противолежащего ребра. Дополнительно нужно хранить ассоциативный массив из пары вершин в ребро для этих вершин. Тогда в момент разделения ребра необходимо удалить это ребро из ассоциативного массива и поместить туда два новых ребра и , которые будут ссылаться на исходное ребро .
Но в очереди могло быть событие по трём вершинам исходного ребра, а после разделения этого ребра уже нет (например, такое может произойти, если с ребром одновременно сталкивается несколько невыпуклых вершин, лежащих на параллельной этому ребру прямой). Посмотрев в ассоциативный массив, можно обнаружить, что такой пары вершин нет. Однако нам нужно всё же получить по ребру требуемую пару вершин. Для этого можно хранить ещё один ассоциативный массив из пар в рёбра, только из него уже не удалять старые пары. Тогда станет возможным получение по паре вершин ребра, а потом по ребру можно будет получить все актуальные пары вершин, соответствующих этому ребру, и добавить с нужной парой вершин.
Алгоритм для невыпуклых полигонов
Шаг 1. Инициализация:
- Положим все вершины в , как это делается в алгоритме для выпуклых многоугольников, а потом поместим в .
- Найдём биссектрисы как в случае с выпуклым многоугольником.
- Для каждой биссектрисы выпуклой вершины найдём ближайшую точку пересечения с биссектрисой соседней вершины, а для невыпуклых вершин найдём также точки пересечения с противолежащими рёбрами (как это описывалось раньше) и положим в приоритетную очередь ближайшую точку пересечения . Будем также с этой точкой хранить её тип — или .
Шаг 2. Пока очередь не пуста:
- Извлечём точку пересечения из приоритетной очереди. Если она имеет тип , то её надо обработать так же, как в шагах алгоритма для выпуклых полигонов. Иначе выполнять шаги ниже.
- Если точка пересечения указывает на уже обработанные вершины, то продолжить со следующей итерации цикла шага 2, как в случае с выпуклым полигоном. По этой причине мы не будем обрабатывать лишние ы, хотя вполне могли их добавить в очередь.
- Нужно сделать примерно то же самое, что и шаге алгоритма для выпуклых многоугольников. Только на этом цикл не завершается, а продолжается с новой итерации, так как многоугольник мог разделиться на несколько частей, и, возможно, мы обработали лишь один подполигон и не последний.
- Добавим в ребро , где точка указывает на вершину . Для ов точки пересечения указывают ровно на одну вершину в .
- Модифицируем теперь :
- пометим вершину как обработанную,
- создадим две новые вершины и с одинаковыми координатами точки пересечения ,
- найдём для каждой вершины и противолежащее ребро в своём подпалигоне,
- разделим с вершиной на две части (как показано на рисунке выше), вставим в части вершины и , а затем обе части добавим в . Вершина будет следующей для предыдующего к узла в и предыдущей для конца противолежащего ребра. Аналогично для вершины ,
- удалим из ассоциативного массива пару вершин ребра и поместим две новых пары, в одной из которых будет вершина и конец ребра , а в другом — начало и вершина ,
- добавим указатели на соответствующие рёбра вершинам и .
- Для обеих вершин и :
- найдём биссектрисы между рёбрами, на которые эти вершины указывают в шаге ,
- найдём все события точек пересечения как в шаге (тут могут получиться события обоих типов),
- сохраним точки пересечения, отвечающие найденным событиям, в приоритетной очереди.
Обработка ов выполняется с такой же асимптотикой, как и в алгоритме для выпуклых полигонов. Но из-за того, что в очередь кладутся всевозможные точки, в которых произошли ы, в ней может оказаться элементов. Хотя обработка а может занять линейное время от числа вершин (если новая вершина в точке пересечения осталась невыпуклой), это произойдёт только для ов, которые создают новые вершины , а их по доказанной лемме. Остальные ы обработаются за в шаге , поэтому итоговая асимптотика составит .
Случай полигонов с дырками
Данный алгоритм может работать и с многоугольниками, содержащими дырки, если они ориентированы по часовой стрелке, чтобы внутренняя область многоугольника лежала слева от рёбер. И в самом начале алгоритма каждый замкнутый контур помещается в свой в множестве .
Пример не для слабонервных
Особенности реализации и другие частные случаи
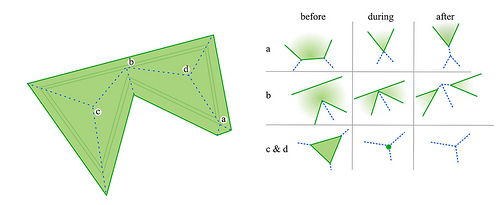
Приведённый здесь алгоритм плох тем (кроме того, что медленно работает), что является довольно общим и не рассматривает возникающие на практике сложные частные случаи. Он будет работать на произвольных случайных полигонах, в которых возникают только простые события (картинка ниже) — в точке произошёл , в точке — , а точки и уже внутри треугольников, и с ними разобраться просто.
Но на практике может возникнуть что-то менее тривиальное (картинка ниже): совпадение многих ов в одной точке, многих ов, или даже в одной точке могут одновременно произойти события двух типов, а также многократное наложение параллельных рёбер друг на друга.
Параллельные противоположные рёбра
С точками и необходимо разбираться следующим образом: как только параллельные рёбра становятся соседними перед событием, нужно проверить, что после произошедшего события они соединятся потом в одно ребро. Если в осталось только два параллельных ребра, то мы удаляем их из .
Ещё примеры не для слабонервных.
Параллельные "соседние" рёбра
Другой интересный случай возникает, когда несоседние параллельные рёбра становятся соседними после исчезания рёбер между ними. Такая проблема называется (parallel consecutive edge problem). В таком случае можно поступать по-разному.
- На левом рисунке используется — согласно этому правилу два ребра рассматриваются отдельно. Тогда верно утверждение, что каждому ребру соответствует ровно одна грань. И в этом случае можно считать, что новая вершина на стыке двух рёбер движется перпендикулярно рёбрам.
- На среднем рисунке используется — рёбра в таком случае объединяются в одно новое ребро.
Отличить этот случай от предыдущего можно, посмотрев на ориентацию двух рёбер. Если они направлены в одну сторону, то это , если в противоположную, то разбираемся как в предыдущем случае.
Множественные события в одной точке
Первая проблема, возникающая в этом случае — точное определение того, что несколько событий произошли в одной точке. Для определения совпадения нескольких событий в одной точке можно поступать приближённо: вводить с каждой точкой -окрестность и смотреть, не попали ли другие точки в эту окрестность, или использовать более точную арифметику[3]. В данном случае недостаточно использовать интервальную арифметику или даже рациональную арифметику. Потому что даже если координаты точек задаются абсолютно точно, то для подсчёта радиуса вписанной окружности необходимо уметь извлекать корни (напомним, что радиус вписанной окружности равен площади, поделённой на полупериметр, а длины сторон треугольников — корни из скалярного произведения векторов разницы точек на самих себя).
Чтобы научиться разбираться с такими случаями в алгоритме, когда мы уже поняли, что в одной точке будет несколько событий, введём понятие обобщённого события пересечения (англ. GIE, generalized intersection event).
Для начала введём понятие цепочек рёбер, которые вовлечены в событие — такие рёбра, которые сталкиваются в данном событии. Эти цепи упорядочим согласно направлению рёбер (см. рисунок выше).
Мы можем также упорядочить сами цепи вокруг точки события, объединив эти цепи в один циклический список. Следовательно, событие получается как бы окружено списком рёбер, которые участвуют в нём, при этом никакие другие рёбра не участвуют. Можно заметить (рисунки выше), что соседние рёбра в списке из изначально разных цепей становятся потом соседними в .
Алгоритм обработки GIE следующий:
- Шаг внутри цепи: в каждой цепи удаляем внутренние рёбра (кроме первого и последнего) — это соответствует тому, что исчезает несколько рёбер, участвующих в одном е. После этого шага остаются цепи только длин или .
- Шаг цепи из одного звена: цепи длины разбиваются в точке события (это соответствует простому у). Теперь все цепи имеют длину ровно .
- Шаг межцепной: объединяем соседние цепи (соответствующие одному событию) в циклический список, соединяя конец одной цепи с началом следующей и так далее. Поэтому каждая цепь разбивается в середине, и образуются новые списки длины .
- Шаг циклы из двух рёбер: списки длины состоящие из двух параллельных рёбер, то есть ограничивающие полигон нулевой площади, удаляются из .
- Шаг PCE: разбираемся с согласно принятому нами правилу решения — правилу слияния или правилу разделения.
В реализации это будет выглядеть следующим образом: можно посмотреть, что сейчас лежит в голове приоритетной очереди, и доставать события, пока они происходят в одной точке, а потом разбить эти события на цепочки и выполнять шаги из алгоритма выше.
Открытые реализации
Приведённый здесь алгоритм был реализован Fernando Cacciola[4], который исправил все ошибки в статье P. Felkel. И этот алгоритм используется в открытой библиотеке вычислительной геометрии CGAL[5]. Более того, он является одной из немногих открытых реализаций построения . Но данный алгоритм достаточно медленный для решения практических задач. В реальной жизни используют его модификации или более сложные алгоритмы.
Другие алгоритмы
Существует простой в понимании и реализации алгоритм для построения на основе триангуляции, который работает за время [6]. Aichholzer смог обобщить этот алгоритм для построения произвольного планарного графа[7]. Также автором в его оригинальной статье был представлен алгоритм построения данной структуры, базирующийся на понятии волнового фронта (англ. wavefront). Этот алгоритм может быть реализован за время с использованием памяти либо с использованием приоритетной очереди за время и памяти[8]. Известен алгоритм построения для монотонных полигонов за время с использованием памяти[9].
Также существует более эффективный алгоритм на основе мотографов, который придумали Stefan Huber и Martin Held. Их реализация называется , и она доступна на их сайте[10].
См. также
Примечания
- ↑ Wikipedia — Fold-and-cut theorem
- ↑ Ambiguous weighted skeleton
- ↑ The GNU MPFR Library
- ↑ Fernando Cacciola, "A CGAL implementation of the Straight Skeleton of a Simple 2D Polygon with Holes "
- ↑ CGAL 4.5 — 2D Straight Skeleton and Polygon Offsetting
- ↑ Stefan Huber, Martin Held, "Straight Skeletons and their Relation to Triangulations"
- ↑ Oswin Aichholzer, Franz Aurenhammera, "Straight Skeletons for General Polygonal Figures in the Plane"
- ↑ Oswin Aichholzer, Franz Aurenhammera, "A Novel Type of Skeleton for Polygons"
- ↑ Therese Biedl, Martin Held, Stefan Huber, Dominik Kaaser, Peter Palfrader, "Straight Skeletons of Monotone Polygons"
- ↑ STALGO — an industrial-strength C++ software package for computing straight skeletons and mitered offset-curves
Источники информации
- Wikipedia — Straight skeleton
- Designing roofs and drawing phylogenetic trees
- Eric Berberich, "Straight Skeleton, Computational Geometry and Geometric Computing Seminar"
- Petr Felkel, Stepan Obdrazalek, "Straight Skeleton Implementation"
- Engineering a weighted straight skeleton algorithm
- Визуализатор алгоритма