BSP-дерево — различия между версиями
м (rollbackEdits.php mass rollback) |
|||
| (не показано 49 промежуточных версий 7 участников) | |||
| Строка 1: | Строка 1: | ||
| − | |||
Одной из важных задач является визуализация объектов, когда точка обзора находится над плоскостью с 3D или 2D объектами. Определение местоположений объектов и их теней занимает много времени. | Одной из важных задач является визуализация объектов, когда точка обзора находится над плоскостью с 3D или 2D объектами. Определение местоположений объектов и их теней занимает много времени. | ||
| + | {{Задача | ||
| + | |definition = | ||
| + | Дана сцена с 2D или 3D объектами и наблюдатель, который смотрит на сцену из своей точки обзора. Нужно отрисовать на сцене видимые наблюдателю части объектов. | ||
| + | }} | ||
| − | === Алгоритм z-буфера === | + | == Простейшие алгоритмы отрисовки сцены == |
| − | Для удаления невидимых частей объектов существует простой, но длительный метод - алгоритм z-буфера. | + | === Алгоритм z-буфера (z-buffer algorithm) === |
| + | Для удаления невидимых частей объектов существует простой, но длительный метод {{---}} алгоритм z-буфера. | ||
В направлении просмотра проводится ось z-координат, затем определяется, какие пиксели покрывают проекции объектов. | В направлении просмотра проводится ось z-координат, затем определяется, какие пиксели покрывают проекции объектов. | ||
Алгоритм хранит информацию об уже обработанных объектах в двух буферах: буфере кадра и z-буфере. | Алгоритм хранит информацию об уже обработанных объектах в двух буферах: буфере кадра и z-буфере. | ||
| Строка 10: | Строка 14: | ||
Предположим, что мы выбрали пиксель и преобразовываем объект. | Предположим, что мы выбрали пиксель и преобразовываем объект. | ||
| − | *Если z-координата объекта в этом пикселе меньше, чем z-координата, хранимая в z-буфере, тогда новый объект лежит перед видимым на данный момент. Тогда запишем цвет нового объекта в буфер кадра, а его координату - в z-буфер. | + | *Если z-координата объекта в этом пикселе меньше, чем z-координата, хранимая в z-буфере, тогда новый объект лежит перед видимым на данный момент. Тогда запишем цвет нового объекта в буфер кадра, а его координату {{---}} в z-буфер. |
*Если z-координата объекта в этом пикселе больше, чем z-координата, хранимая в z-буфере, то новый объект не видим, и буферы останутся без изменений. | *Если z-координата объекта в этом пикселе больше, чем z-координата, хранимая в z-буфере, то новый объект не видим, и буферы останутся без изменений. | ||
Алгоритм z-буфера легко реализовать, и он быстро работает. Поэтому именно этот метод используют чаще всего, но у него есть свой недостаток: для хранения z-буфера требуется большое количество памяти, кроме того, требуется дополнительная проверка каждого пикселя, покрываемого объектом. | Алгоритм z-буфера легко реализовать, и он быстро работает. Поэтому именно этот метод используют чаще всего, но у него есть свой недостаток: для хранения z-буфера требуется большое количество памяти, кроме того, требуется дополнительная проверка каждого пикселя, покрываемого объектом. | ||
| − | === Алгоритм художника === | + | === Алгоритм художника (painter's algorithm) === |
| − | Алгоритм художника избегает дополнительных затрат памяти, изначально сортируя объекты по расстоянию от них до точки обзора. Тогда объекты проверяются в так называемом порядке глубины, начиная от самого дальнего. В таком случае при | + | [[Файл:painters_algo.png|500px|right]] |
| + | Алгоритм художника избегает дополнительных затрат памяти, изначально сортируя объекты по расстоянию от них до точки обзора. Тогда объекты проверяются в так называемом порядке глубины, начиная от самого дальнего. В таком случае при рассмотрении объекта уже не нужна проверка его z-координаты, мы всегда пишем цвет в буфер кадра. Значения, хранимые в буфере ранее, просто перезаписываются. | ||
| − | + | [[Файл:triangle_cycle.png|150px|left]] | |
| − | Когда такое цикличное перекрытие происходит, объекты не могут быть корректно отсортированы. | + | Чтобы успешно применять данный метод, нужно уметь быстро сортировать объекты. К сожалению, это не всегда просто. Кроме того, порядок глубины не всегда существует: отношение "перед" может содержать циклы. Когда такое цикличное перекрытие происходит, объекты не могут быть корректно отсортированы. В таком случае мы должны разорвать циклы, разбив один или более объектов на части. |
| − | В таком случае мы должны разорвать циклы, разбив один или более объектов на части. | ||
| − | Определение, какие объекты нужно разбить и где, затем сортировка их фрагментов - дорогой процесс, так как порядок зависит от положения точки обзора, и мы должны пересчитывать все при каждом ее смещении. | + | Определение, какие объекты нужно разбить и где, затем сортировка их фрагментов {{---}} дорогой процесс, так как порядок зависит от положения точки обзора, и мы должны пересчитывать все при каждом ее смещении. |
Чтобы использовать этот алгоритм в реальной жизни, например, в симуляторе полета, мы должны предпосчитать сцену так, чтобы можно было быстро найти корректный порядок отображения объектов для любой точки обзора. | Чтобы использовать этот алгоритм в реальной жизни, например, в симуляторе полета, мы должны предпосчитать сцену так, чтобы можно было быстро найти корректный порядок отображения объектов для любой точки обзора. | ||
| − | |||
| − | + | Данную задачу можно элегантно решить при помощи техники '''двоичного разбиения пространства''' (англ. ''binary space partitioning, BSP''). | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | == Структура BSP-дерева == | |
| − | + | Чтобы понять, что из себя представляет двоичное разбиение пространства, рассмотрим рисунок. На нем показано двоичное разбиение множества объектов на плоскости и дерево, которое этому разбиению соответствует. | |
| − | + | В двумерном случае BSP строится с помощью рекурсивного разбиения плоскости прямыми. В данном примере это происходит так: сначала проводим прямую <tex>l_1</tex>, разбивая полуплоскость выше <tex>l_1</tex> прямой <tex>l_2</tex>, а ниже {{---}} прямой <tex>l_3</tex> и так далее. | |
| − | |||
| − | + | [[Файл:bsp_plane1.png|300px]][[Файл:bsp_tree1.png|300px]] | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | Прямые разбивают на части не только плоскость, но и объекты, расположенные на ней. Разбиение продолжается до тех пор, пока внутри каждой грани плоскости окажется не более одного фрагмента объекта. | |
| − | |||
| − | |||
| − | |||
| − | + | Этот процесс можно представить с помощью двоичного дерева. Каждый лист дерева соответствует грани разбиения, в нем хранится фрагмент объекта, находящийся внутри этой грани. Каждый узел дерева соответсвует разбивающей прямой, которая хранится в этом узле. | |
| + | {{Определение | ||
| + | | definition = '''BSP-дерево''' (англ. ''binary space partition tree'') {{---}} дерево, отвечающее заданному двоичному разбиению пространства. | ||
| + | }} | ||
| + | Опишем подробней свойства BSP-дерева. | ||
| + | |||
| + | Рассмотрим гиперплоскость <tex>h: a_1 \cdot x_1 + a_2 \cdot x_2 + \ldots + a_d \cdot x_d + a_{d + 1} = 0</tex>. | ||
| + | |||
| + | Пусть <tex>h^+</tex> {{---}} положительное полупространство, а <tex>h^-</tex> {{---}} отрицательное: | ||
| + | |||
| + | <tex>h^+ = \{(x_1,\ x_2,\ \dots,\ x_d) \mid a_1 \cdot x_1 + a_2 \cdot x_2 + \ldots + a_d \cdot x_d + a_{d + 1} > 0\}</tex> | ||
| + | |||
| + | <tex>h^- = \{(x_1,\ x_2,\ \dots,\ x_d) \mid a_1 \cdot x_1 + a_2 \cdot x_2 + \ldots + a_d \cdot x_d + a_{d + 1} < 0\}</tex> | ||
| + | |||
| + | Пусть <tex>S</tex> {{---}} множество объектов, для которого мы строим разбиение в <tex>d</tex>-мерном пространстве. | ||
| + | |||
| + | Пусть <tex>v</tex> {{---}} какая-то вершина дерева, тогда обозначим за <tex>S(v)</tex> множество объектов (возможно пустое), хранимых в этой вершине. | ||
| + | |||
| + | BSP-дерево <tex>T</tex> для этого множества обектов обладает следующими свойствами: | ||
| + | *Если <tex>|S| \leqslant 1</tex>, то <tex>T</tex> {{---}} лист. Фрагмент объекта в <tex>S</tex>, если он существует, хранится в этом листе. | ||
| + | *Если <tex>|S| > 1</tex>, то в корне дерева <tex>v</tex> хранится гиперплоскость <tex>h_v</tex> и множество <tex>S(v)</tex> объектов, которые полностью содержатся в <tex>h_v</tex>. | ||
| + | **левый ребенок <tex>v</tex> является корнем BSP-дерева <tex>T^-</tex> на множестве объектов <tex>S^- = \{h_v^- \cap s \mid s \in S\}</tex>; | ||
| + | **правый ребенок <tex>v</tex> является корнем BSP-дерева <tex>T^+</tex> на множестве объектов <tex>S^+ = \{h_v^+ \cap s \mid s \in S\}</tex>. | ||
| + | |||
| + | Размер BSP-дерева равен суммарному размеру множеств во всех узлах. Другими словами, размер BSP-дерева {{---}} число фрагментов, на которые были разбиты объекты. Так как BSP-дерево не содержит бесполезные прямые (прямые, которые разбивают пустую грань), то количество узлов пропорционально размеру дерева. | ||
| + | |||
| + | [[Файл:bsp_plane2.png|300px]][[Файл:bsp_tree2.png|300px]] | ||
| + | |||
| + | Листья BSP-дерева соответствуют граням, то есть мы можем каждой вершине <tex>v</tex> сопоставить полигональную область на плоскости, которая определяется как пересечение полуплоскостей <tex>h_{\mu}^{\Diamond}</tex>, где <tex>\mu</tex> {{---}} предок <tex>v</tex>, и | ||
| + | |||
| + | <tex> | ||
| + | \Diamond = \left\{\begin{array}{llcl} | ||
| + | - & \mathrm{if}\ v\ - \ \mathrm{left}\ \mathrm{child} \\ | ||
| + | + & \mathrm{if}\ v\ - \ \mathrm{right}\ \mathrm{child} \\ | ||
| + | \end{array}\right. | ||
| + | </tex> | ||
| − | |||
Корню дерева соответсвует все пространство. | Корню дерева соответсвует все пространство. | ||
| − | |||
| − | При построении BSP-дерева могут использоваться любые разбивающие гиперплоскости. В целях упрощения вычислений может быть удобно ограничить множество доступных разбивающих гиперплоскостей. | + | Таким образом, серая область на рисунке соответствует региону <tex>l_1^+ \cap l_2^+ \cap l_3^-</tex>. |
| − | + | ||
| − | + | При построении BSP-дерева могут использоваться любые разбивающие гиперплоскости. В целях упрощения вычислений может быть удобно ограничить множество доступных разбивающих гиперплоскостей. Обычно используют авто-разбиения. | |
| − | + | {{Определение | |
| − | + | | definition = В двумерном случае для множества отрезков разбиение, в котором используются разбивающие прямые, проходящие через один из данных отрезков, называется '''авто-разбивающим''' (англ. ''auto-partition''). | |
| − | + | }} | |
| + | |||
| + | В трёхмерном случае авто-разбиение использует плоскости, которые содержат грани многогранников. | ||
| + | |||
| + | [[Файл:bsp_n2.png|130px]] | ||
| + | |||
| + | Как видно из рисунка, размер авто-разбивающего дерева может быть не минимальным. Возможен случай, когда размер BSP-дерева может составлять <tex>\mathcal{O}(n^2) </tex>, где <tex> n = |S| </tex>. | ||
== BSP-деревья и алгоритм художника == | == BSP-деревья и алгоритм художника == | ||
| − | Предположим, что мы построили BSP-дерево T для множества объектов S в трехмерном пространстве. Как нам следует использовать его, чтобы получить порядок глубины для алгоритма художника? | + | Предположим, что мы построили BSP-дерево <tex>T</tex> для множества объектов <tex>S</tex> в трехмерном пространстве. Как нам следует использовать его, чтобы получить порядок глубины для алгоритма художника? |
| − | Пусть | + | |
| − | Тогда ни один из объектов, лежащих под этой плоскостью, не может | + | Пусть <tex>p_{view}</tex> {{---}} точка обзора, и она лежит над разбивающей плоскостью, хранимой в корне <tex>T</tex>. |
| + | |||
| + | Тогда ни один из объектов, лежащих под этой плоскостью, не может перекрыть ни один из объектов, лежащих выше нее. Таким образом, мы можем безопасно отрисовать фрагменты объектов из поддерева <tex>T^-</tex> до отрисовки объектов из поддерва <tex>T^+</tex>. | ||
Порядок фрагментов объектов в поддеревьях определяется таким же способом. | Порядок фрагментов объектов в поддеревьях определяется таким же способом. | ||
| − | painters_algorithm(T, | + | <code> |
| − | + | '''void''' painters_algorithm(<tex>T</tex>, <tex>p_{view}</tex>): | |
| − | + | <tex>v \leftarrow T.root</tex> | |
| − | + | '''if''' <tex>v</tex> {{---}} лист | |
| − | + | отрисовать фрагменты объектов из <tex>S(v)</tex> | |
| − | + | '''else if''' <tex>p_{view} \in h_v^+</tex> | |
| − | + | painters_algorithm(<tex>T^-</tex>, <tex>p_{view}</tex>) | |
| − | + | отрисовать фрагменты объектов из <tex>S(v)</tex> | |
| − | + | painters_algorithm(<tex>T^+</tex>, <tex>p_{view}</tex>) | |
| − | + | '''else if''' <tex>p_{view} \in h_v^-</tex> | |
| − | + | painters_algorithm(<tex>T^+</tex>, <tex>p_{view}</tex>) | |
| − | + | отрисовать фрагменты объектов из <tex>S(v)</tex> | |
| − | + | painters_algorithm(<tex>T^-</tex>, <tex>p_{view}</tex>) | |
| − | + | '''else''' <font color="green">/∗ <tex>p_{view} \in h_v</tex> ∗/</font> | |
| − | + | painters_algorithm(<tex>T^+</tex>, <tex>p_{view}</tex>) | |
| + | painters_algorithm(<tex>T^-</tex>, <tex>p_{view}</tex>) | ||
| + | </code> | ||
| − | Заметим, что мы не рисуем | + | Заметим, что мы не рисуем объекты из <tex>S(v)</tex>, когда <tex>p_{view}</tex> лежит на разбивающей плоскости <tex>h_v</tex>, потому что они являются плоскими двумерными полигонами. |
| − | Эффективность данного алгоритма, как и любого другого алгоритма для BSP-деревьев, зависит от размера BSP-дерева. То есть | + | Эффективность данного алгоритма, как и любого другого алгоритма для BSP-деревьев, зависит от размера BSP-дерева. То есть необходимо выбирать разбивающие плоскости таким образом, чтобы фрагментация объектов была минимальной. |
| − | + | ||
| − | + | BSP-деревья интересны тем, что позволяют достичь быстрой реализации удаления скрытых поверхностей для отрисовки сцены (будь то симулятор полёта или персонаж в игре, осматривающий окружающий мир). Так как скорость {{---}} главная цель, следует упростить вид объектов рассматриваемого пейзажа, поэтому далее будем считать, что в 3D мы работаем только с многогранниками, грани которых уже [[Триангуляция полигонов (ушная + монотонная) | триангулированы]]. Таким образом множество <tex>S</tex> в трёхмерном пространстве будет состоять только из треугольников. | |
| − | |||
== Построение BSP-дерева == | == Построение BSP-дерева == | ||
| − | + | Прежде чем переходить к задаче отрисовки сцены в трёхмерном случае, рассмотрим для простоты аналогичную задачу на плоскости. | |
| − | Пусть S - множество из n непересекающихся отрезков на плоскости. Ограничимся авто-разбиением, рассматривая только прямые, содержащие один из отрезков. | + | |
| − | Пусть l(s) - прямая, содержащая отрезок s. | + | Пусть <tex>S</tex> {{---}} множество из <tex>n</tex> непересекающихся отрезков на плоскости. Ограничимся авто-разбиением, рассматривая только прямые, содержащие один из отрезков. |
| − | На вход алгоритму подается S = { | + | |
| + | Пусть <tex>l(s)</tex> {{---}} прямая, содержащая отрезок <tex>s</tex>. | ||
| + | |||
| + | На вход алгоритму подается <tex>S = \{s_1,\ s_2,\ \dots ,\ s_n\}</tex> {{---}} множество отрезков. | ||
| + | |||
| + | <code> | ||
| + | '''BSPTree''' 2D_BSP_tree(<tex>S</tex>): | ||
| + | '''if''' <tex>|S| \leqslant 1</tex> | ||
| + | <tex>T \leftarrow</tex> '''BSPTree'''(<tex>S</tex>) <font color="green">/* <tex>T</tex> будет листом, в котором хранится данное множество */</font> | ||
| + | '''return''' <tex>T</tex> | ||
| + | '''else''' <font color="green">/* используем <tex>l(s_1)</tex> как разбивающую прямую */</tex></font> | ||
| + | <tex>S^+ \leftarrow \{s \cap l^+(s_1) \mid s \in S\}</tex> | ||
| + | <tex>T^+ \leftarrow</tex> 2D_BSP_tree(<tex>S^+</tex>) | ||
| + | <tex>S^- \leftarrow \{s \cap l^-(s_1) \mid s \in S\}</tex> | ||
| + | <tex>T^- \leftarrow</tex> 2D_BSP_tree(<tex>S^-</tex>) | ||
| + | <tex>S_v \leftarrow \{s \in S \mid s \subset l(s_1)\}</tex> | ||
| + | <tex>T \leftarrow</tex> '''BSPTree'''(<tex>S_v,\ T^-,\ T^+</tex>) | ||
| + | <font color="green">// создаем BSP-дерево c корнем в вершине <tex>v</tex>, левым поддеревом <tex>T^-</tex> и правым поддеревом <tex>T^+</tex> </font> | ||
| + | <font color="green">// и множеством хранимых объектов <tex>S_v</tex></font> | ||
| + | '''return''' <tex>T</tex> | ||
| + | </code> | ||
| + | Данный алгоритм создает BSP-дерево для множества <tex>S</tex>, но как уже известно, оно не будет наименьшим в общем случае. | ||
| + | |||
| + | Необходимо придумать стратегию выбора прямой разбиения, а не просто брать <tex>l(s_1)</tex>. Возможным подходом является выбор отрезка <tex>s \in S</tex>, такого что <tex>l(s)</tex> пересекает наименьшее число отрезков. Но такой жадный алгоритм работает не на всех конфигурациях отрезков. Кроме того, поиск такого отрезка {{---}} занятие затратное. | ||
| + | |||
| + | Как и в других алгоритмах, когда нужно сделать сложный выбор, сделаем рандомный выбор. Это означает, что для разбиения мы будем использовать случайно выбранный отрезок. Для этого перед тем, как начинать построение дерева, расположим отрезки в <tex>S</tex> случайном порядке. | ||
| + | |||
| + | <code> | ||
| + | '''void''' 2D_random_BSP_tree(<tex>S</tex>): | ||
| + | <tex>S \leftarrow </tex> random_permutation(<tex>S</tex>) | ||
| + | <tex>T \leftarrow </tex> 2D_BSP_tree(<tex>S</tex>) | ||
| + | '''return''' <tex>T</tex> | ||
| + | </code> | ||
| + | Перед анализированием рандомизированного алгоритма рассмотрим одну простую оптимизацию. | ||
| + | |||
| + | Предположим, что мы выбрали несколько первых разбивающих прямых. Эти прямые порождают разбиение плоскости, грани которой соответствуют каким-то узлам BSP-дерева. | ||
| + | |||
| + | [[Файл:bsp_free.png|300px|right]] | ||
| + | Рассмотрим одну из таких граней <tex>f</tex>. В <tex>S</tex> могут быть отрезки, которые полностью пересекают <tex>f</tex>. Выбор одного из таких отрезков для разбиения <tex>f</tex> не вызовет фрагментации других отрезков внутри <tex>f</tex>, так как данный отрезок исключается из дальнейшего рассмотрения. Назовем такое свободным разбиением. | ||
| + | |||
| + | Нашей улучшенной стратегией будет использование свободных разбиений везде, где только можно, и использование случайных разбиений в противном случае. Для реализации данной оптимизации нужно уметь определять, вызывает ли отрезок свободное разбиение. Для этого сопоставим каждому отрезку две булевых переменных, которые покажут, лежат ли правый и левый концы отрезка на какой-то из уже добавленных разбивающих прямых. Обе переменных истинны, когда отрезок вызывает свободное разбиение. | ||
| + | |||
| + | Теперь оценим производительность алгоритма '''2D_random_BSP_tree'''. Для упрощения рассуждений будем анализировать версию без свободных разбиений (асимптотической разницы между ними нет). Начнем с анализа размера BSP-дерева, равного числу полученных фрагментов, которое зависит от сгенерированной перестановки отрезков. Некоторые перестановки могут породить маленькие деревья, а другие {{---}} большие. | ||
| + | |||
| + | [[Файл:bsp_three_segments.png|500px]] | ||
| + | |||
| + | В качестве примера рассмотрим три отрезка, изображенные на рисунке. Если они рассматриваются в порядке (a), то мы получаем пять фрагментов, если же в порядке (b) {{---}} то всего три фрагмента. | ||
| + | |||
| + | Так как размер BSP-дерева зависит от сгенерированной перестановки, будем анализировать ожидаемый размер BSP-дерева {{---}} средний размер для всех <tex>n!</tex> перестановок. | ||
| + | |||
| + | {{Лемма | ||
| + | | statement = Ожидаемое число фрагментов, сгенерированных алгоритмом '''2D_random_BSP_tree''' есть <tex>\mathcal{O}(n \log n)</tex>. | ||
| + | |proof = | ||
| + | Пусть <tex>s_i</tex> {{---}} фиксированный отрезок из <tex>S</tex>. Проанализируем [[Математическое ожидание случайной величины | ожидаемое]] количество отрезков, которые мы разрежем, когда <tex>l(s_i)</tex> будет добавлена алгоритмом как следующая разбивающая прямая. | ||
| − | + | Рассмотрим рисунок и постараемся понять, разрезается ли отрезок <tex>s_j</tex> при добавлении прямой <tex>l(s_i)</tex>, в зависимости от отрезков, которые разрезаны <tex>l(s_i)</tex>, но находятся между <tex>s_i</tex> и <tex>s_j</tex>. | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | В частности, когда прямая, пересекающая такой отрезок, добавляется раньше <tex>l(s_i)</tex>, она закрывает <tex>s_j</tex> от <tex>s_i</tex>. На рисунке (b) так происходит с отрезком <tex>s_3</tex>, который защищен отрезком <tex>s_1</tex> от <tex>s_2</tex>. | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | Эти размышления приводят нас к определению расстояния от какого-то отрезка до фиксированного отрезка <tex>s_i</tex>. | |
| − | |||
| − | |||
| − | |||
| − | + | [[Файл:bsp_dist.png|300px|right]] | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | <tex> | |
| − | + | \mathrm{dist}(s_i, s_j) = \left\{\begin{array}{llcl} | |
| − | + | |\{s\ \mathrm{between}\ s_i\ \mathrm{and}\ s_j \mid l(s_i) \cap s \ne \varnothing \}| & \mathrm{if}\ l(s_i) \cap s_j \ne \varnothing \\ | |
| − | + | \infty & \mathrm{otherwise} \\ | |
| + | \end{array}\right. | ||
| + | </tex> | ||
| + | |||
| + | Для всех конечных расстояний до отрезка <tex>s_i</tex> может быть только два отрезка с одинаковым расстоянием {{---}} те, что лежат по разные стороны от <tex>s_i</tex>. | ||
| + | |||
| + | Пусть <tex>k = \mathrm{dist}(s_i, s_j)</tex> и <tex>s_{j_1},\ s_{j_2},\ \ldots ,\ s_{j_k}</tex> {{---}} отрезки между <tex>s_i</tex> и <tex>s_j</tex>. | ||
| + | |||
| + | Найдём вероятность того, что при добавлении <tex>l(s_i)</tex> разрежет <tex>s_j</tex>. Чтобы это произошло, <tex>s_i</tex> должен быть рассмотрен перед <tex>s_j</tex> и перед любым из отрезков между <tex>s_i</tex> и <tex>s_j</tex>, иначе они бы защитили <tex>s_j</tex> от <tex>s_i</tex>. Другими словами, среди множества индексов <tex>\{i,\ j,\ j_1,\ \ldots ,\ j_k\}</tex> индекс <tex>i</tex> должен быть наименьшим. | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
Так как отрезки расположены в случайном порядке, получаем: | Так как отрезки расположены в случайном порядке, получаем: | ||
| − | P(l(s_i) | + | <tex>P(l(s_i) \cap s_j \ne \varnothing) \leqslant \genfrac{}{}{}{0}{1}{k + 2}</tex> |
| − | + | ||
| − | Теперь мы можем ограничить ожидаемое число разрезов, происходящих при добавлении s_i: | + | Существуют отрезки, которые не разрезаются <tex>l(s_i)</tex>, но расширение которых защитит <tex>s_j</tex>, так что выше записано неравенство. |
| − | E(число разрезов, происходящих при добавлении s_i) | + | |
| − | По линейности ожиданий мы можем заключить, что ожидаемое число разрезов, вызванных добавлением всех отрезков составляет не более | + | Теперь мы можем ограничить ожидаемое число разрезов, происходящих при добавлении <tex>s_i</tex>: |
| − | Так как изначально даны n отрезков, ожидаемое число фрагментов ограничено n + | + | |
| + | <tex>E(</tex>число разрезов, происходящих при добавлении <tex>s_i) \leqslant \sum\limits_{j \ne i} \genfrac{}{}{}{0}{1}{\mathrm{dist}(s_i, s_j) + 2} \leqslant 2 \cdot \sum\limits_{k=0}^{n - 2} \genfrac{}{}{}{0}{1}{k + 2} \leqslant 2 \ln n</tex>. | ||
| + | |||
| + | По линейности ожиданий мы можем заключить, что ожидаемое число разрезов, вызванных добавлением всех отрезков составляет не более <tex>2n\log n</tex>. Так как изначально даны <tex>n</tex> отрезков, ожидаемое число фрагментов ограничено <tex>n + 2n\log n</tex>. | ||
| + | }} | ||
| + | |||
| + | Было показано, что ожидаемый размер BSP-дерева, построенного с помощью алгоритма '''2D_random_BSP_tree''', составляет <tex>n + 2n\log n</tex>. Следовательно, мы доказали, что BSP-дерево размера <tex>n + 2n\log n</tex> существует для любого множества <tex>n</tex> отрезков. Кроме того, хотя бы половина перестановок приводит к BSP-дереву размера <tex>n + 4n\log n</tex>. | ||
| − | |||
Мы можем использовать этот факт, чтобы найти дерево такого размера: после запуска алгоритма сравним размер дерева с данной оценкой, если он превышает оценку, просто построим BSP-дерево еще раз, но для новой перестановки. Ожидаемое число запусков равняется двум. | Мы можем использовать этот факт, чтобы найти дерево такого размера: после запуска алгоритма сравним размер дерева с данной оценкой, если он превышает оценку, просто построим BSP-дерево еще раз, но для новой перестановки. Ожидаемое число запусков равняется двум. | ||
| − | Теперь проанализируем время работы алгоритма. Понятно, что оно зависит от используемой перестановки, так что опять рассмотрим ожидаемое время работы. Нахождение рандомной перестановки занимает O(n). | + | Теперь проанализируем время работы алгоритма. Понятно, что оно зависит от используемой перестановки, так что опять рассмотрим ожидаемое время работы. Нахождение рандомной перестановки занимает <tex>\mathcal{O}(n)</tex> при помощи [[Метод генерации случайной перестановки, алгоритм Фишера-Йетса |алгоритма Фишера-Йетса]]. Если проигнорировать время рекурсивных вызовов, то время работы алгоритма линейно от количества фрагментов в <tex>S</tex>. Это число не превышает <tex>n</tex>, так как становится меньше с каждым рекурсивным вызовом. Число рекурсивных вызовов ограничено количеством сгенерированных фрагментов, которое составляет <tex>\mathcal{O}(n\log n)</tex>. Таким образом, время построения дерева составляет <tex>\mathcal{O}(n^2\log n)</tex>. |
| − | Если проигнорировать время рекурсивных вызовов, то время работы алгоритма линейно от количества фрагментов в S. Это число не превышает n, так как становится меньше с каждым рекурсивным вызовом. | + | |
| − | Число рекурсивных вызовов ограничено количеством сгенерированных фрагментов, которое составляет O( | + | {{Теорема |
| + | | statement = В двумерном пространстве BSP-дерево размера <tex>\mathcal{O}(n\log n)</tex> может быть построено за ожидаемое время <tex>\mathcal{O}(n^2\log n)</tex>. | ||
| + | }} | ||
| + | |||
| + | Описанный выше алгоритм легко обобщается на трёхмерное пространство. Как было упомянуто выше, мы считаем, что работаем в 3D с триангуляцией граней многранников. | ||
| + | |||
| + | Пусть <tex>S</tex> {{---}} множество непересекающихся треугольков в <tex>\mathbb{R}^3</tex>. | ||
| + | |||
| + | Снова ограничимся только авто-разбиениями, разбивая пространство плоскостями, содержащими какой-то из треугольников. | ||
| + | |||
| + | Для треугольника <tex>t</tex> обозначим плоскость, содержащую его, как <tex>h(t)</tex>. | ||
| + | На вход алгоритму подается множество треугольников <tex>S = \{t_1,\ t_2,\ \dots ,\ t_n\}</tex>, заданных в трехмерном пространстве. | ||
| − | + | '''BSPTree''' 3D_BSP_tree(<tex>S</tex>): | |
| − | + | '''if''' <tex>|S| \leqslant 1</tex> | |
| + | <tex>T \leftarrow</tex> '''BSPTree'''(<tex>S</tex>) <font color="green">/* <tex>T</tex> будет листом, в котором хранится данное множество */</font> | ||
| + | '''return''' <tex>T</tex> | ||
| + | '''else''' <font color="green">/* используем <tex>h(t_1)</tex> как разбивающую плоскость */</font> | ||
| + | <tex>S^+ \leftarrow \{t \cap h^+(t_1) \mid t \in S\}</tex> | ||
| + | <tex>T^+ \leftarrow</tex> 3D_BSP_tree(<tex>S^+</tex>) | ||
| + | <tex>S^- \leftarrow \{t \cap h^-(t_1) \mid t \in S\}</tex> | ||
| + | <tex>T^- \leftarrow</tex> 3D_BSP_tree(<tex>S^-</tex>) | ||
| + | <tex>S_v \leftarrow \{t \in S \mid t \subset h(t_1)\}</tex> | ||
| + | <tex>T \leftarrow</tex> '''BSPTree'''(<tex>S_v,\ T^-,\ T^+</tex>) | ||
| + | <font color="green">// создаем BSP-дерево c корнем в вершине <tex>v</tex>, левым поддеревом <tex>T^-</tex> и правым поддеревом <tex>T^+</tex> </font> | ||
| + | <font color="green">// и множеством хранимых объектов <tex>S_v</tex></font> | ||
| + | '''return''' <tex>T</tex> | ||
| − | + | Размер полученного BSP-дерева снова зависит от порядка треугольников. Как и в двумерном случае, мы можем попытаться получить хороший ожидаемый размер дерева, переставив треугольники в случайном порядке. На практике это дает хорошие результаты. | |
| − | |||
| − | На | ||
| − | + | == См. также == | |
| − | + | * [[Перечисление точек в произвольном прямоугольнике за n * log ^(d - 1) n (range tree)]] | |
| − | + | * [[Дерево интервалов (interval tree) и пересечение точки с множеством интервалов]] | |
| − | + | * [[Пересечение прямоугольника с множеством непересекающихся отрезков (segment tree)]] | |
| − | + | == Источники иформации == | |
| − | + | * Mark de Berg, Marc van Kreveld, Mark Overmars, and Otfried Schwarzkopf (2000), Computational Geometry (2nd revised ed.), Springer-Verlag, ISBN 3-540-65620-0 Chapter 12: Binary Space Partition: pp.259–267. | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | [[Категория: Вычислительная геометрия]] | |
| + | [[Категория: Аффинное пространство]] | ||
| + | [[Категория: Структуры данных]] | ||
Текущая версия на 19:31, 4 сентября 2022
Одной из важных задач является визуализация объектов, когда точка обзора находится над плоскостью с 3D или 2D объектами. Определение местоположений объектов и их теней занимает много времени.
| Задача: |
| Дана сцена с 2D или 3D объектами и наблюдатель, который смотрит на сцену из своей точки обзора. Нужно отрисовать на сцене видимые наблюдателю части объектов. |
Содержание
Простейшие алгоритмы отрисовки сцены
Алгоритм z-буфера (z-buffer algorithm)
Для удаления невидимых частей объектов существует простой, но длительный метод — алгоритм z-буфера. В направлении просмотра проводится ось z-координат, затем определяется, какие пиксели покрывают проекции объектов. Алгоритм хранит информацию об уже обработанных объектах в двух буферах: буфере кадра и z-буфере.
- В буфере кадра для каждого пикселя хранится информация о цвете объекта, отображаемого им на данный момент.
- В z-буфере для каждого пикселя хранится z-координата видимого на данный момент объекта, точнее, в нем хранится z-координату точки такого объекта.
Предположим, что мы выбрали пиксель и преобразовываем объект.
- Если z-координата объекта в этом пикселе меньше, чем z-координата, хранимая в z-буфере, тогда новый объект лежит перед видимым на данный момент. Тогда запишем цвет нового объекта в буфер кадра, а его координату — в z-буфер.
- Если z-координата объекта в этом пикселе больше, чем z-координата, хранимая в z-буфере, то новый объект не видим, и буферы останутся без изменений.
Алгоритм z-буфера легко реализовать, и он быстро работает. Поэтому именно этот метод используют чаще всего, но у него есть свой недостаток: для хранения z-буфера требуется большое количество памяти, кроме того, требуется дополнительная проверка каждого пикселя, покрываемого объектом.
Алгоритм художника (painter's algorithm)
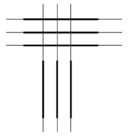
Алгоритм художника избегает дополнительных затрат памяти, изначально сортируя объекты по расстоянию от них до точки обзора. Тогда объекты проверяются в так называемом порядке глубины, начиная от самого дальнего. В таком случае при рассмотрении объекта уже не нужна проверка его z-координаты, мы всегда пишем цвет в буфер кадра. Значения, хранимые в буфере ранее, просто перезаписываются.
Чтобы успешно применять данный метод, нужно уметь быстро сортировать объекты. К сожалению, это не всегда просто. Кроме того, порядок глубины не всегда существует: отношение "перед" может содержать циклы. Когда такое цикличное перекрытие происходит, объекты не могут быть корректно отсортированы. В таком случае мы должны разорвать циклы, разбив один или более объектов на части.
Определение, какие объекты нужно разбить и где, затем сортировка их фрагментов — дорогой процесс, так как порядок зависит от положения точки обзора, и мы должны пересчитывать все при каждом ее смещении. Чтобы использовать этот алгоритм в реальной жизни, например, в симуляторе полета, мы должны предпосчитать сцену так, чтобы можно было быстро найти корректный порядок отображения объектов для любой точки обзора.
Данную задачу можно элегантно решить при помощи техники двоичного разбиения пространства (англ. binary space partitioning, BSP).
Структура BSP-дерева
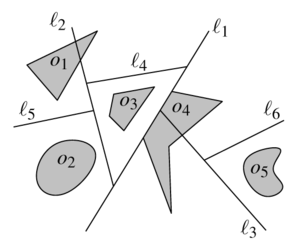
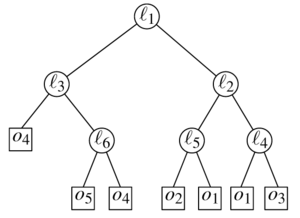
Чтобы понять, что из себя представляет двоичное разбиение пространства, рассмотрим рисунок. На нем показано двоичное разбиение множества объектов на плоскости и дерево, которое этому разбиению соответствует. В двумерном случае BSP строится с помощью рекурсивного разбиения плоскости прямыми. В данном примере это происходит так: сначала проводим прямую , разбивая полуплоскость выше прямой , а ниже — прямой и так далее.
Прямые разбивают на части не только плоскость, но и объекты, расположенные на ней. Разбиение продолжается до тех пор, пока внутри каждой грани плоскости окажется не более одного фрагмента объекта.
Этот процесс можно представить с помощью двоичного дерева. Каждый лист дерева соответствует грани разбиения, в нем хранится фрагмент объекта, находящийся внутри этой грани. Каждый узел дерева соответсвует разбивающей прямой, которая хранится в этом узле.
| Определение: |
| BSP-дерево (англ. binary space partition tree) — дерево, отвечающее заданному двоичному разбиению пространства. |
Опишем подробней свойства BSP-дерева.
Рассмотрим гиперплоскость .
Пусть — положительное полупространство, а — отрицательное:
Пусть — множество объектов, для которого мы строим разбиение в -мерном пространстве.
Пусть — какая-то вершина дерева, тогда обозначим за множество объектов (возможно пустое), хранимых в этой вершине.
BSP-дерево для этого множества обектов обладает следующими свойствами:
- Если , то — лист. Фрагмент объекта в , если он существует, хранится в этом листе.
- Если , то в корне дерева хранится гиперплоскость и множество объектов, которые полностью содержатся в .
- левый ребенок является корнем BSP-дерева на множестве объектов ;
- правый ребенок является корнем BSP-дерева на множестве объектов .
Размер BSP-дерева равен суммарному размеру множеств во всех узлах. Другими словами, размер BSP-дерева — число фрагментов, на которые были разбиты объекты. Так как BSP-дерево не содержит бесполезные прямые (прямые, которые разбивают пустую грань), то количество узлов пропорционально размеру дерева.
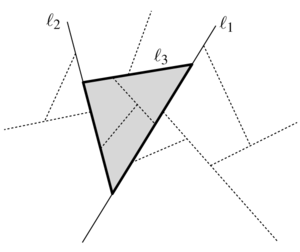
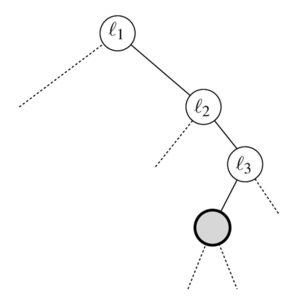
Листья BSP-дерева соответствуют граням, то есть мы можем каждой вершине сопоставить полигональную область на плоскости, которая определяется как пересечение полуплоскостей , где — предок , и
Корню дерева соответсвует все пространство.
Таким образом, серая область на рисунке соответствует региону .
При построении BSP-дерева могут использоваться любые разбивающие гиперплоскости. В целях упрощения вычислений может быть удобно ограничить множество доступных разбивающих гиперплоскостей. Обычно используют авто-разбиения.
| Определение: |
| В двумерном случае для множества отрезков разбиение, в котором используются разбивающие прямые, проходящие через один из данных отрезков, называется авто-разбивающим (англ. auto-partition). |
В трёхмерном случае авто-разбиение использует плоскости, которые содержат грани многогранников.
Как видно из рисунка, размер авто-разбивающего дерева может быть не минимальным. Возможен случай, когда размер BSP-дерева может составлять , где .
BSP-деревья и алгоритм художника
Предположим, что мы построили BSP-дерево для множества объектов в трехмерном пространстве. Как нам следует использовать его, чтобы получить порядок глубины для алгоритма художника?
Пусть — точка обзора, и она лежит над разбивающей плоскостью, хранимой в корне .
Тогда ни один из объектов, лежащих под этой плоскостью, не может перекрыть ни один из объектов, лежащих выше нее. Таким образом, мы можем безопасно отрисовать фрагменты объектов из поддерева до отрисовки объектов из поддерва . Порядок фрагментов объектов в поддеревьях определяется таким же способом.
void painters_algorithm(, ): if — лист отрисовать фрагменты объектов из else if painters_algorithm(, ) отрисовать фрагменты объектов из painters_algorithm(, ) else if painters_algorithm(, ) отрисовать фрагменты объектов из painters_algorithm(, ) else /∗ ∗/ painters_algorithm(, ) painters_algorithm(, )
Заметим, что мы не рисуем объекты из , когда лежит на разбивающей плоскости , потому что они являются плоскими двумерными полигонами.
Эффективность данного алгоритма, как и любого другого алгоритма для BSP-деревьев, зависит от размера BSP-дерева. То есть необходимо выбирать разбивающие плоскости таким образом, чтобы фрагментация объектов была минимальной.
BSP-деревья интересны тем, что позволяют достичь быстрой реализации удаления скрытых поверхностей для отрисовки сцены (будь то симулятор полёта или персонаж в игре, осматривающий окружающий мир). Так как скорость — главная цель, следует упростить вид объектов рассматриваемого пейзажа, поэтому далее будем считать, что в 3D мы работаем только с многогранниками, грани которых уже триангулированы. Таким образом множество в трёхмерном пространстве будет состоять только из треугольников.
Построение BSP-дерева
Прежде чем переходить к задаче отрисовки сцены в трёхмерном случае, рассмотрим для простоты аналогичную задачу на плоскости.
Пусть — множество из непересекающихся отрезков на плоскости. Ограничимся авто-разбиением, рассматривая только прямые, содержащие один из отрезков.
Пусть — прямая, содержащая отрезок .
На вход алгоритму подается — множество отрезков.
BSPTree 2D_BSP_tree(): if BSPTree() /* будет листом, в котором хранится данное множество */ return else /* используем как разбивающую прямую */</tex> 2D_BSP_tree() 2D_BSP_tree() BSPTree() // создаем BSP-дерево c корнем в вершине , левым поддеревом и правым поддеревом // и множеством хранимых объектов return
Данный алгоритм создает BSP-дерево для множества , но как уже известно, оно не будет наименьшим в общем случае.
Необходимо придумать стратегию выбора прямой разбиения, а не просто брать . Возможным подходом является выбор отрезка , такого что пересекает наименьшее число отрезков. Но такой жадный алгоритм работает не на всех конфигурациях отрезков. Кроме того, поиск такого отрезка — занятие затратное.
Как и в других алгоритмах, когда нужно сделать сложный выбор, сделаем рандомный выбор. Это означает, что для разбиения мы будем использовать случайно выбранный отрезок. Для этого перед тем, как начинать построение дерева, расположим отрезки в случайном порядке.
void 2D_random_BSP_tree(): random_permutation() 2D_BSP_tree() return
Перед анализированием рандомизированного алгоритма рассмотрим одну простую оптимизацию.
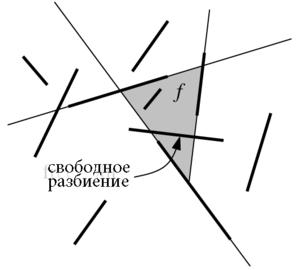
Предположим, что мы выбрали несколько первых разбивающих прямых. Эти прямые порождают разбиение плоскости, грани которой соответствуют каким-то узлам BSP-дерева.
Рассмотрим одну из таких граней . В могут быть отрезки, которые полностью пересекают . Выбор одного из таких отрезков для разбиения не вызовет фрагментации других отрезков внутри , так как данный отрезок исключается из дальнейшего рассмотрения. Назовем такое свободным разбиением.
Нашей улучшенной стратегией будет использование свободных разбиений везде, где только можно, и использование случайных разбиений в противном случае. Для реализации данной оптимизации нужно уметь определять, вызывает ли отрезок свободное разбиение. Для этого сопоставим каждому отрезку две булевых переменных, которые покажут, лежат ли правый и левый концы отрезка на какой-то из уже добавленных разбивающих прямых. Обе переменных истинны, когда отрезок вызывает свободное разбиение.
Теперь оценим производительность алгоритма 2D_random_BSP_tree. Для упрощения рассуждений будем анализировать версию без свободных разбиений (асимптотической разницы между ними нет). Начнем с анализа размера BSP-дерева, равного числу полученных фрагментов, которое зависит от сгенерированной перестановки отрезков. Некоторые перестановки могут породить маленькие деревья, а другие — большие.
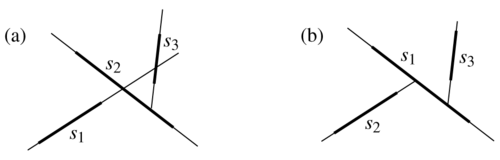
В качестве примера рассмотрим три отрезка, изображенные на рисунке. Если они рассматриваются в порядке (a), то мы получаем пять фрагментов, если же в порядке (b) — то всего три фрагмента.
Так как размер BSP-дерева зависит от сгенерированной перестановки, будем анализировать ожидаемый размер BSP-дерева — средний размер для всех перестановок.
| Лемма: |
Ожидаемое число фрагментов, сгенерированных алгоритмом 2D_random_BSP_tree есть . |
| Доказательство: |
|
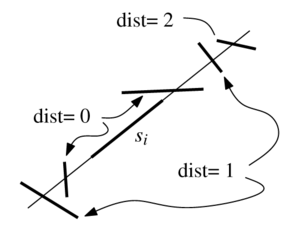
Пусть — фиксированный отрезок из . Проанализируем ожидаемое количество отрезков, которые мы разрежем, когда будет добавлена алгоритмом как следующая разбивающая прямая. Рассмотрим рисунок и постараемся понять, разрезается ли отрезок при добавлении прямой , в зависимости от отрезков, которые разрезаны , но находятся между и . В частности, когда прямая, пересекающая такой отрезок, добавляется раньше , она закрывает от . На рисунке (b) так происходит с отрезком , который защищен отрезком от . Эти размышления приводят нас к определению расстояния от какого-то отрезка до фиксированного отрезка .
Для всех конечных расстояний до отрезка может быть только два отрезка с одинаковым расстоянием — те, что лежат по разные стороны от . Пусть и — отрезки между и . Найдём вероятность того, что при добавлении разрежет . Чтобы это произошло, должен быть рассмотрен перед и перед любым из отрезков между и , иначе они бы защитили от . Другими словами, среди множества индексов индекс должен быть наименьшим. Так как отрезки расположены в случайном порядке, получаем: Существуют отрезки, которые не разрезаются , но расширение которых защитит , так что выше записано неравенство. Теперь мы можем ограничить ожидаемое число разрезов, происходящих при добавлении : число разрезов, происходящих при добавлении . По линейности ожиданий мы можем заключить, что ожидаемое число разрезов, вызванных добавлением всех отрезков составляет не более . Так как изначально даны отрезков, ожидаемое число фрагментов ограничено . |
Было показано, что ожидаемый размер BSP-дерева, построенного с помощью алгоритма 2D_random_BSP_tree, составляет . Следовательно, мы доказали, что BSP-дерево размера существует для любого множества отрезков. Кроме того, хотя бы половина перестановок приводит к BSP-дереву размера .
Мы можем использовать этот факт, чтобы найти дерево такого размера: после запуска алгоритма сравним размер дерева с данной оценкой, если он превышает оценку, просто построим BSP-дерево еще раз, но для новой перестановки. Ожидаемое число запусков равняется двум.
Теперь проанализируем время работы алгоритма. Понятно, что оно зависит от используемой перестановки, так что опять рассмотрим ожидаемое время работы. Нахождение рандомной перестановки занимает при помощи алгоритма Фишера-Йетса. Если проигнорировать время рекурсивных вызовов, то время работы алгоритма линейно от количества фрагментов в . Это число не превышает , так как становится меньше с каждым рекурсивным вызовом. Число рекурсивных вызовов ограничено количеством сгенерированных фрагментов, которое составляет . Таким образом, время построения дерева составляет .
| Теорема: |
В двумерном пространстве BSP-дерево размера может быть построено за ожидаемое время . |
Описанный выше алгоритм легко обобщается на трёхмерное пространство. Как было упомянуто выше, мы считаем, что работаем в 3D с триангуляцией граней многранников.
Пусть — множество непересекающихся треугольков в .
Снова ограничимся только авто-разбиениями, разбивая пространство плоскостями, содержащими какой-то из треугольников.
Для треугольника обозначим плоскость, содержащую его, как . На вход алгоритму подается множество треугольников , заданных в трехмерном пространстве.
BSPTree 3D_BSP_tree(): if BSPTree() /* будет листом, в котором хранится данное множество */ return else /* используем как разбивающую плоскость */ 3D_BSP_tree() 3D_BSP_tree() BSPTree() // создаем BSP-дерево c корнем в вершине , левым поддеревом и правым поддеревом // и множеством хранимых объектов return
Размер полученного BSP-дерева снова зависит от порядка треугольников. Как и в двумерном случае, мы можем попытаться получить хороший ожидаемый размер дерева, переставив треугольники в случайном порядке. На практике это дает хорошие результаты.
См. также
- Перечисление точек в произвольном прямоугольнике за n * log ^(d - 1) n (range tree)
- Дерево интервалов (interval tree) и пересечение точки с множеством интервалов
- Пересечение прямоугольника с множеством непересекающихся отрезков (segment tree)
Источники иформации
- Mark de Berg, Marc van Kreveld, Mark Overmars, and Otfried Schwarzkopf (2000), Computational Geometry (2nd revised ed.), Springer-Verlag, ISBN 3-540-65620-0 Chapter 12: Binary Space Partition: pp.259–267.