Избыточное кодирование, код Хэмминга — различия между версиями
Glukos (обсуждение | вклад) |
м (rollbackEdits.php mass rollback) |
||
| (не показано 59 промежуточных версий 13 участников) | |||
| Строка 1: | Строка 1: | ||
| − | + | '''Избыточное кодирование''' (англ. ''redundant encoding'') {{---}} вид кодирования, использующий избыточное количество информации с целью последующего контроля целостности данных при записи/воспроизведении информации или при её передаче по линиям связи. | |
| − | '''Избыточное кодирование''' - вид кодирования, использующий избыточное количество информации с целью последующего контроля целостности данных при записи/воспроизведении информации или при её передаче по линиям связи. | + | |
| + | {{Определение | ||
| + | |definition=Код определяет <tex>d</tex> ошибок, если при передаче кодового слова, в котором <tex>\leq d</tex> ошибок, алгоритм декодирования скажет, что есть ошибка. | ||
| + | }} | ||
| + | |||
| + | {{Определение | ||
| + | |definition=Код исправляет <tex>d</tex> ошибок, если при передаче кодового слова, в котором <tex>\leq d</tex> ошибок, алгоритм декодирования сможет восстановить исходное слово. | ||
| + | }} | ||
| + | |||
== Код, определяющий одну ошибку == | == Код, определяющий одну ошибку == | ||
| − | Увеличив объем кода на 1 бит, можно получить возможность определять при передаче наличие одной ошибки. Для этого к коду нужно добавить бит x: <tex>0110..10x</tex>, такой, чтобы сумма всех | + | Увеличив объем кода на <tex>1</tex> бит, можно получить возможность определять при передаче наличие одной ошибки. Для этого к коду нужно добавить бит <tex>x</tex>: <tex>0110..10x</tex>, такой, чтобы сумма всех единиц была четной. В случае, если контрольная сумма окажется нечетной, следует отправить запрос на повторную посылку элемента, в котором была обнаружена ошибка. Такое кодирование применяется только если вероятность ошибки крайне мала, например, в оперативной памяти компьютера. |
== Кодирование Хэмминга == | == Кодирование Хэмминга == | ||
Кодирование Хэмминга предусматривает как возможность обнаружения ошибки, так и возможность её исправления. | Кодирование Хэмминга предусматривает как возможность обнаружения ошибки, так и возможность её исправления. | ||
| − | Рассмотрим простой пример | + | Рассмотрим простой пример {{---}} закодируем четыре бита: <tex>a, b, c, d</tex>. Полученный код будет иметь длину <tex>8</tex> бит и выглядеть следующим образом: <tex>a,b,c,d, a \oplus b, c \oplus d, a \oplus c, b \oplus d.</tex> |
Рассмотрим табличную визуализацию кода: | Рассмотрим табличную визуализацию кода: | ||
| − | {| border=" | + | {| class="wikitable" style="width:10cm" border=1 |
| − | ! <tex>a</tex> || <tex>b</tex> || <tex>a \oplus b</tex> | + | |-align="center" bgcolor=#F0F0F0 |
| − | |- | + | ! <tex>a</tex> || <tex>b</tex> ||style="background:#FFF"| <tex bgcolor=#FFF>a \oplus b</tex> |
| − | ! <tex>c</tex> || <tex>d</tex> || <tex>c \oplus d</tex> | + | |-align="center" bgcolor=#F0F0F0 |
| − | |- | + | ! <tex>c</tex> || <tex>d</tex> ||style="background:#FFF"| <tex>c \oplus d</tex> |
| − | + | |-align="center" bgcolor=#FFF | |
| + | |<tex>a \oplus c</tex> || <tex> b \oplus d </tex> | ||
|} | |} | ||
| − | Как видно из таблицы, даже если один из битов <tex>a, b, c, d</tex> передался с ошибкой, содержащие его <tex>xor | + | Как видно из таблицы, даже если один из битов <tex>a, b, c, d</tex> передался с ошибкой, содержащие его <tex>xor</tex>-суммы не сойдутся. Итого, зная строку и столбец в проиллюстрированной таблице можно точно исправить ошибочный бит. Если один из битов <tex>a \oplus b, a \oplus c, b \oplus d, c\oplus d</tex> передался с ошибкой, то не сойдется только одна сумма и очевидно, что можно легко определить, какой бит неверный |
| + | |||
| + | По аналогичному принципу можно закодировать любое число бит. Пусть мы имеем исходную строку длиной в <tex>2^k</tex> бит. Для получения её кода добавим к ней <tex>k</tex> пар бит по следующему принципу: | ||
| + | *Первая пара: сумма четных бит и сумма нечетных бит | ||
| + | *Вторая пара: сумма тех бит, в чьем номере второй бит с конца ноль и сумма тех бит, в чьем номере второй бит с конца единица | ||
| + | ... | ||
| + | *<tex>k</tex>-тая пара: сумма тех бит, в чьем номере <tex>k</tex>-тый бит с конца ноль и сумма тех бит, в чьем номере <tex>k</tex>-тый бит с конца единица<br> | ||
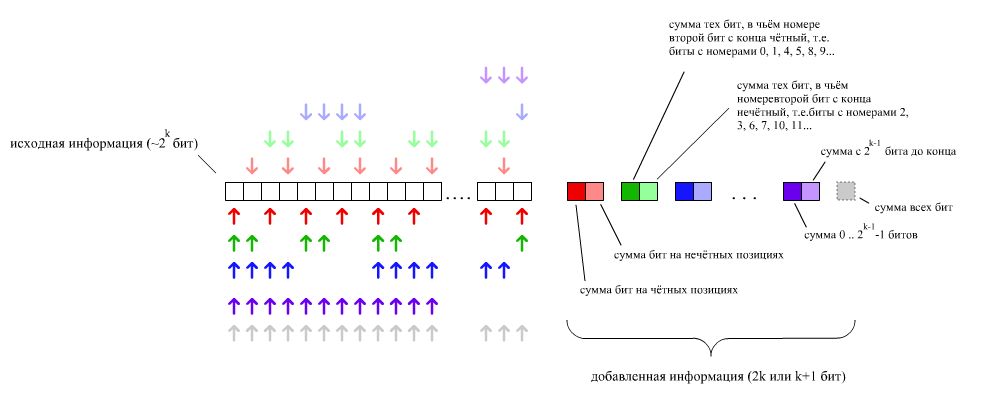
| + | [[Файл:Ham3.jpg|1000px|thumb|left|Соответствие добавленной информации исходным битам. Первый вариант кодирования соответствует использованию битов, раскрашенных в тёмные и светлые цвета, оптимизация — в тёмные цвета и серый]] | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | Легко понять, что если в одном бите из строки допущена ошибка, то с помощью дописанных <tex>k</tex> пар бит можно точно определить, какой именно бит ошибочный. Это объясняется тем, что каждая пара определяет один бит номера ошибочного бита в строке. Всего пар <tex>k</tex>, следовательно мы имеем <tex>k</tex> бит номера ошибочного бита, что вполне достаточно: общее число бит строки не превосходит <tex>2^k+2k</tex>. | ||
| + | |||
| + | Теперь заметим, что в случае наличия ошибки в исходной строке, ровно один бит в каждой паре будет равен единице. Тогда можно оставить только один бит из пары. Однако этого будет недостаточно, поскольку если только один добавленный бит не соответствует строке, то нельзя понять, ошибка в нём или в строке. На этот случай можно добавить ещё один контрольный бит {{---}} <tex> \mathrm X \mathrm O \mathrm R</tex> всех битов строки. | ||
| + | |||
| + | Итого, увеличивая код длиной <tex>n</tex> на <tex>\log_2 n + 1</tex>, можно обнаружить и исправить одну ошибку. | ||
| + | |||
| + | == См. также == | ||
| + | * [[Обнаружение и исправление ошибок кодирования]] | ||
| + | == Источники информации == | ||
| + | *[http://en.wikipedia.org/wiki/Hamming_code Wikipedia {{---}} Hamming code] | ||
| + | |||
| + | [[Категория: Дискретная математика и алгоритмы]] | ||
| + | |||
| + | [[Категория: Алгоритмы сжатия ]] | ||
Текущая версия на 19:41, 4 сентября 2022
Избыточное кодирование (англ. redundant encoding) — вид кодирования, использующий избыточное количество информации с целью последующего контроля целостности данных при записи/воспроизведении информации или при её передаче по линиям связи.
| Определение: |
| Код определяет ошибок, если при передаче кодового слова, в котором ошибок, алгоритм декодирования скажет, что есть ошибка. |
| Определение: |
| Код исправляет ошибок, если при передаче кодового слова, в котором ошибок, алгоритм декодирования сможет восстановить исходное слово. |
Код, определяющий одну ошибку
Увеличив объем кода на бит, можно получить возможность определять при передаче наличие одной ошибки. Для этого к коду нужно добавить бит : , такой, чтобы сумма всех единиц была четной. В случае, если контрольная сумма окажется нечетной, следует отправить запрос на повторную посылку элемента, в котором была обнаружена ошибка. Такое кодирование применяется только если вероятность ошибки крайне мала, например, в оперативной памяти компьютера.
Кодирование Хэмминга
Кодирование Хэмминга предусматривает как возможность обнаружения ошибки, так и возможность её исправления. Рассмотрим простой пример — закодируем четыре бита: . Полученный код будет иметь длину бит и выглядеть следующим образом: Рассмотрим табличную визуализацию кода:
Как видно из таблицы, даже если один из битов передался с ошибкой, содержащие его -суммы не сойдутся. Итого, зная строку и столбец в проиллюстрированной таблице можно точно исправить ошибочный бит. Если один из битов передался с ошибкой, то не сойдется только одна сумма и очевидно, что можно легко определить, какой бит неверный
По аналогичному принципу можно закодировать любое число бит. Пусть мы имеем исходную строку длиной в бит. Для получения её кода добавим к ней пар бит по следующему принципу:
- Первая пара: сумма четных бит и сумма нечетных бит
- Вторая пара: сумма тех бит, в чьем номере второй бит с конца ноль и сумма тех бит, в чьем номере второй бит с конца единица
...
- -тая пара: сумма тех бит, в чьем номере -тый бит с конца ноль и сумма тех бит, в чьем номере -тый бит с конца единица
Легко понять, что если в одном бите из строки допущена ошибка, то с помощью дописанных пар бит можно точно определить, какой именно бит ошибочный. Это объясняется тем, что каждая пара определяет один бит номера ошибочного бита в строке. Всего пар , следовательно мы имеем бит номера ошибочного бита, что вполне достаточно: общее число бит строки не превосходит .
Теперь заметим, что в случае наличия ошибки в исходной строке, ровно один бит в каждой паре будет равен единице. Тогда можно оставить только один бит из пары. Однако этого будет недостаточно, поскольку если только один добавленный бит не соответствует строке, то нельзя понять, ошибка в нём или в строке. На этот случай можно добавить ещё один контрольный бит — всех битов строки.
Итого, увеличивая код длиной на , можно обнаружить и исправить одну ошибку.