Обсуждение:Мощность множества — различия между версиями
(Новая страница: «TODO: А вот тут должна какая-то биекция, доказывающая это утверждение. <tex> \begin{pmatrix} a_{11} & a_{12} & …») |
м |
||
| (не показано 5 промежуточных версий 3 участников) | |||
| Строка 7: | Строка 7: | ||
Картинка примерно такая(сорри за ужасные стрелки, рисовал наспех): [[Файл:8c1d5ad692def320763a95e5d46b7af8.png]] | Картинка примерно такая(сорри за ужасные стрелки, рисовал наспех): [[Файл:8c1d5ad692def320763a95e5d46b7af8.png]] | ||
Ровно такую же картинку можно использовать для доказательства счетности рационального множества. [[Участник:Dmitriy D.|Dmitriy D.]] 02:16, 21 ноября 2010 (UTC) | Ровно такую же картинку можно использовать для доказательства счетности рационального множества. [[Участник:Dmitriy D.|Dmitriy D.]] 02:16, 21 ноября 2010 (UTC) | ||
| + | |||
| + | |||
| + | == Мощность R == | ||
| + | Как-то странно и внезапно что это доказывается с помощью непонятно какой-то левой и богомерзкой фукнции - тангенса. Наверное есть что-то более строгое?) --[[Участник:Dgerasimov|Дмитрий Герасимов]] | ||
| + | :Имха, всё вполне логично) чем тебе тангенс не угодил? [[Участник:SkudarnovYaroslav|SkudarnovYaroslav]] 09:46, 3 января 2011 (UTC) | ||
| + | |||
| + | :имхо - аналогично, тангенс - хорошая функция. Не думаю, что для её строгого определения (то есть через ряды) необходимо знать мощность вещественной оси, и тогда логического круга тут не будет. А вообще говоря, вроде подойдет любая функция, с хотя бы одной вертикальной асимптотой, тангенс в этом плане просто очень удобен и нагляден [[Участник:Dmitriy D.|Dmitriy D.]] 16:43, 3 января 2011 (UTC) | ||
| + | :: Просто у нас как бы упор на то что мы все досконально и с самого начала, последовательно выводим - а тут на те, тангенс. Разрыв шаблона у меня в общем) --[[Участник:Dgerasimov|Дмитрий Герасимов]] | ||
Текущая версия на 20:41, 3 января 2011
TODO: А вот тут должна какая-то биекция, доказывающая это утверждение.
Биекция здесь простая: нужно просто пройтись по диагоналям матрицы в порядке и пронумеровать их соответственно. Таким образом каждого элемента будет номер и по каждому номеру можно найти элемент матрицы. Таким образом получим биекцию с натуральным множеством.
Картинка примерно такая(сорри за ужасные стрелки, рисовал наспех): 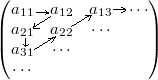 Ровно такую же картинку можно использовать для доказательства счетности рационального множества. Dmitriy D. 02:16, 21 ноября 2010 (UTC)
Ровно такую же картинку можно использовать для доказательства счетности рационального множества. Dmitriy D. 02:16, 21 ноября 2010 (UTC)
Мощность R
Как-то странно и внезапно что это доказывается с помощью непонятно какой-то левой и богомерзкой фукнции - тангенса. Наверное есть что-то более строгое?) --Дмитрий Герасимов
- Имха, всё вполне логично) чем тебе тангенс не угодил? SkudarnovYaroslav 09:46, 3 января 2011 (UTC)
- имхо - аналогично, тангенс - хорошая функция. Не думаю, что для её строгого определения (то есть через ряды) необходимо знать мощность вещественной оси, и тогда логического круга тут не будет. А вообще говоря, вроде подойдет любая функция, с хотя бы одной вертикальной асимптотой, тангенс в этом плане просто очень удобен и нагляден Dmitriy D. 16:43, 3 января 2011 (UTC)
- Просто у нас как бы упор на то что мы все досконально и с самого начала, последовательно выводим - а тут на те, тангенс. Разрыв шаблона у меня в общем) --Дмитрий Герасимов