Совершенное паросочетание в кубическом графе — различия между версиями
м (rollbackEdits.php mass rollback) |
|||
| (не показано 90 промежуточных версий 5 участников) | |||
| Строка 1: | Строка 1: | ||
| + | ==Лемма о сравнимости по модулю 2== | ||
| + | {{Лемма | ||
| + | |id = lemma1 | ||
| + | |statement = | ||
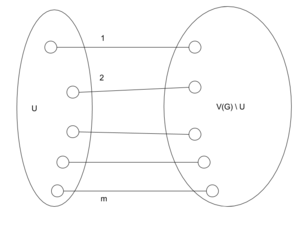
| + | Пусть <tex>G</tex> {{---}} <tex>k</tex>-[[Основные определения теории графов#defRegularGraph |регулярный граф]], <tex>U \in V(G)</tex>, <tex>|U|</tex> нечётно, <tex>m</tex> {{---}} число рёбер, соединяющих вершины множества <tex>U</tex> с вершинами из <tex>V(G) \setminus U</tex>. Тогда <tex>m \equiv k \pmod 2</tex> | ||
| + | |proof = | ||
| + | [[Файл:Сравнимость.png|300px|thumb|left|Иллюстрация к лемме]] | ||
| + | <tex>m = (\sum\limits_{v \in U} d_G(v)) - 2e(G(U))</tex>, где <tex>e(G(U))</tex> {{---}} количество рёбер, соединяющих вершину из <tex>U</tex> с другой вершиной из <tex>U</tex>. | ||
| + | |||
| + | тогда <tex>m = k|U| - 2e(G(U))</tex>. | ||
| + | |||
| + | <tex>2e(G(U))</tex> чётно, поэтому <tex>m \equiv k|U| \pmod 2</tex>. Так как <tex> |U|</tex> нечётно, <tex>m \equiv k \pmod 2</tex>. | ||
| + | }} | ||
| + | |||
| + | ==Теорема Петерсона (Petersen)== | ||
| + | {{Определение | ||
| + | |id=cube_graf_def | ||
| + | |definition= '''Кубический граф''' (англ. ''Cubic graph'') {{---}} [[Основные определения: граф, ребро, вершина, степень, петля, путь, цикл| граф]], в котором все вершины имеют степень три. Другими словами, кубический граф является <tex>3</tex>-регулярным.}} | ||
| + | |||
{{Теорема | {{Теорема | ||
| − | |id=th1 | + | |id=th1 |
|author=Петерсон | |author=Петерсон | ||
| − | |statement= | + | |statement = Пусть <tex>G</tex>{{---}}[[Отношение связности, компоненты связности#connected_graph | связный]] кубический граф, в котором не более <tex>2</tex> [[Мост, эквивалентные определения | мостов]]. Тогда в <tex>G</tex> есть [[Паросочетания: основные определения, теорема о максимальном паросочетании и дополняющих цепях#perfect_matching | совершенное паросочетание]]. |
| + | |proof = | ||
| + | Предположим, что совершенного паросочетания в <tex>G</tex> нет, тогда можно выбрать [[Теорема Татта о существовании полного паросочетания#Tutt_set | множество Татта]] <tex>S \subset V(G)</tex>. | ||
| + | |||
| + | Пусть <tex>U_1, \ldots, U_n</tex> {{---}} все нечётные компоненты связности графа <tex>G \setminus S</tex>. <tex>m_i</tex> {{---}} количество ребёр <tex>G</tex>, связывающих вершины <tex>U_i</tex> с вершинами <tex>S</tex>. | ||
| + | |||
| + | По предыдущей лемме, все <tex>m_i</tex> нечётны. Так как не более чем два ребра графа <tex>G</tex> {{---}} мосты, то не более, чем два числа из <tex>m_1, \ldots, m_n</tex> равны <tex>1</tex>, остальные числа не менее <tex>3</tex>. | ||
| + | |||
| + | Так как <tex>S</tex> {{---}} множество Татта, то <tex>odd(G \setminus S) > |S|</tex>. Так как количество вершин кубического графа <tex>G</tex> чётно, мы имеем <tex>S \neq \emptyset, odd(G \setminus S) \equiv S \pmod 2</tex>, следовательно, <tex>n = odd(G \setminus S) \geqslant |S| + 2</tex>. Тогда | ||
| + | |||
| + | <tex>\sum\limits_{v \in S} d_G(v) \geqslant \sum\limits_{i = 1}^n m_i \geqslant 3n - 4 \geqslant 3(|S| + 2) - 4 = 3|S| | ||
| + | + 2 > 3|S| = \sum\limits_{v \in S} d_G(v)</tex>, что, очевидно, невозможно. | ||
| + | |||
| + | Найдено противоречие, следовательно, множество Татта выбрать невозможно, следовательно, в <tex>G</tex> есть совершенное паросочетание. | ||
| + | }} | ||
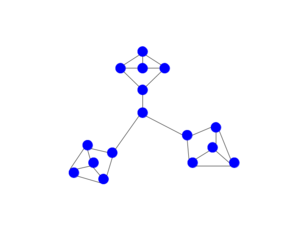
| − | + | [[Файл:Петерсен 3 моста.png|300px|thumb|left|Кубический граф с тремя мостами, в котором не существует совершенного паросочетания.]] | |
| − | + | Заметим, что утверждение теоремы не может быть усилено до большего числа мостов, так как для случая с тремя мостами существует контрпример. | |
| + | ==Теорема Фринка (Frink)== | ||
{{Теорема | {{Теорема | ||
|id=th2. | |id=th2. | ||
| Строка 12: | Строка 46: | ||
|statement= | |statement= | ||
| − | Пусть <tex>G(V, E)</tex> | + | Пусть <tex>G = (V, E)</tex> {{---}} двусвязный кубический граф. |
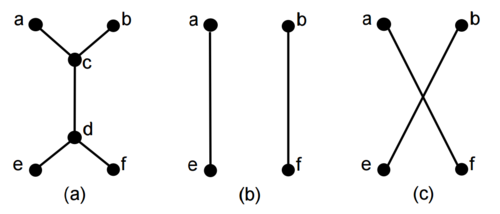
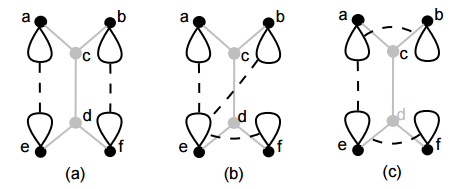
| − | Возьмём ребро <tex>p = (c, d)</tex>. Пусть вершины <tex>a</tex> и <tex>b</tex> | + | Возьмём ребро <tex>p = (c, d)</tex>. Пусть вершины <tex>a</tex> и <tex>b</tex> смежны с вершиной <tex>c</tex>, а вершины <tex>e</tex> и <tex>f</tex> смежны с вершиной <tex>d</tex> (рисунок <tex>1 (a)</tex>). |
| − | Как минимум одно из двух сокращений графа <tex>G</tex>, состоящее из удаления вершин <tex>c, d</tex> и пересоединения вершин <tex>a, b, e, f</tex> рёбрами <tex>(a, e), (b, f)</tex> или <tex>(a, f), (b, e)</tex> (рисунок <tex>1 (b), (c)</tex>) сохранит двусвязность графа. | + | Как минимум одно из двух сокращений графа <tex>G</tex>, состоящее из удаления вершин <tex>c, d</tex> и пересоединения вершин <tex>a, b, e, f</tex> рёбрами <tex>(a, e), (b, f)</tex> или <tex>(a, f), (b, e)</tex> (рисунок <tex>1 (b), (c)</tex>, рисунок <tex>2</tex>) сохранит двусвязность графа. |
|proof= | |proof= | ||
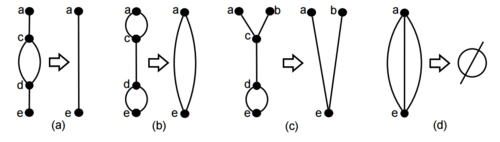
| − | Обозначим компоненты графа <tex>G(V - {c, d})</tex> как <tex>A, B, E, F</tex>, которые содержат вершины <tex>a, b, e, f</tex> соответственно. Так как <tex>G</tex> не имеет мостов (соответственно <tex>p</tex> не является мостом) должно существовать ребро, соединяющее одну из компонент <tex>A</tex> или <tex>B</tex>, с одной из компонент <tex>E</tex> или <tex>F</tex>. Без потери общности предположим, что <tex>A</tex> соединено с <tex>E</tex>. Заметим, что рёбра <tex>(b, c), (d, f)</tex> так же не являются мостами, значит возможны три случая (с учётом изоморфизма) (рисунок <tex>3</tex>): | + | Обозначим компоненты графа <tex>G(V - \{c, d\})</tex> как <tex>A, B, E, F</tex>, которые содержат вершины <tex>a, b, e, f</tex> соответственно. Так как <tex>G</tex> не имеет мостов (соответственно <tex>p</tex> не является мостом) должно существовать ребро, соединяющее одну из компонент <tex>A</tex> или <tex>B</tex>, с одной из компонент <tex>E</tex> или <tex>F</tex>. Без потери общности предположим, что <tex>A</tex> соединено с <tex>E</tex>. Заметим, что рёбра <tex>(b, c), (d, f)</tex> так же не являются мостами, значит возможны три случая (с учётом изоморфизма) (рисунок <tex>3</tex>): |
| − | * компонента <tex>B</tex> соединена с <tex>F</tex> | + | * компонента <tex>B</tex> соединена с <tex>F</tex>, |
| − | * компонента <tex>B</tex> соединена с <tex>E</tex> и компонента <tex>E</tex> соединена с <tex>F</tex> | + | * компонента <tex>B</tex> соединена с <tex>E</tex> и компонента <tex>E</tex> соединена с <tex>F</tex>, |
| − | * компонента <tex>A</tex> соединена с <tex>B</tex> и компонента <tex>E</tex> соединена с <tex>F</tex> | + | * компонента <tex>A</tex> соединена с <tex>B</tex> и компонента <tex>E</tex> соединена с <tex>F</tex>. |
| − | Во всех трёх случаях если <tex>G(V - {c, d})</tex> расширить рёбрами <tex>(a, f), (b, e)</tex> (получим граф <tex>G'</tex>), добавленные рёбра будут лежать на некотором цикле в <tex>G'</tex> (рисунок <tex>4</tex>). Так же | + | Во всех трёх случаях если <tex>G(V - \{c, d\})</tex> расширить рёбрами <tex>(a, f), (b, e)</tex> (получим граф <tex>G'</tex>), добавленные рёбра будут лежать на некотором [[Основные определения: граф, ребро, вершина, степень, петля, путь, цикл| цикле]] в <tex>G'</tex> (рисунок <tex>4</tex>). Так же для любой пары вершин <tex>u, v</tex> <math>\in</math> <tex>\{a, b, e, f\}</tex> существует цикл в <tex>G'</tex>, содержащий данные вершины. Чтобы доказать, что <tex>G'</tex> двусвязен, нужно показать, что каждое ребро <tex>r</tex> из <tex>G'</tex> лежит на некотором цикле в <tex>G'</tex>. Пусть цикл <tex>C</tex> в <tex>G</tex> содержит <tex>r</tex> (такой цикл существует, так как <tex>G</tex> двусвязен). Если <tex>C</tex> не проходит через вершины <tex>c, d</tex> тогда <tex>C</tex> так же является циклом в <tex>G'</tex>, иначе построим цикл <tex>C'</tex> графа <tex>G'</tex> из <tex>C</tex> следующим образом: |
* если путь <tex> x - c - d - y </tex> <math>\in</math> <tex> C </tex>, <tex> x </tex> <math>\in</math> <tex> \{a, b\} </tex>, <tex> y </tex> <math>\in</math> <tex> \{e, f\} </tex>, удалим этот путь и добавим любой другой из <tex> x </tex> в <tex> y </tex> в <tex> G' </tex>, не содержащий <tex>r</tex> (такой путь всегда существует, так как <tex> x </tex> и <tex> y </tex> принадлежат некоторому циклу в <tex> G' </tex>), | * если путь <tex> x - c - d - y </tex> <math>\in</math> <tex> C </tex>, <tex> x </tex> <math>\in</math> <tex> \{a, b\} </tex>, <tex> y </tex> <math>\in</math> <tex> \{e, f\} </tex>, удалим этот путь и добавим любой другой из <tex> x </tex> в <tex> y </tex> в <tex> G' </tex>, не содержащий <tex>r</tex> (такой путь всегда существует, так как <tex> x </tex> и <tex> y </tex> принадлежат некоторому циклу в <tex> G' </tex>), | ||
* если путь <tex> a - c - b </tex> <math>\in</math> <tex> C </tex>, удалим этот путь и добавим любой другой из <tex> a </tex> в <tex> b </tex> в <tex> G' </tex>, не содержащий <tex>r</tex>, | * если путь <tex> a - c - b </tex> <math>\in</math> <tex> C </tex>, удалим этот путь и добавим любой другой из <tex> a </tex> в <tex> b </tex> в <tex> G' </tex>, не содержащий <tex>r</tex>, | ||
| Строка 31: | Строка 65: | ||
{|align="center" | {|align="center" | ||
|-valign="center" | |-valign="center" | ||
| − | |[[Файл:Frinks_algorithm1.png|thumb| | + | |[[Файл:Frinks_algorithm1.png|thumb|500px|Рисунок 1. Сокращение двусвязного кубического графа. <tex>(a)</tex> Нужно удалить вершины <tex>c, d</tex>. <tex>(b)</tex> первый тип сокращения {{---}} вершина <tex>a</tex> соединена с <tex>e</tex>, вершина <tex>b</tex> соединена с <tex>f</tex>. <tex>(c)</tex> второй тип сокращений {{---}} вершина <tex>a</tex> соединена с <tex>f</tex>, вершина <tex>b</tex> соединена с <tex>e</tex>.]] |
| − | |[[Файл:Frinks_algorithm2.PNG|thumb| | + | |[[Файл:Frinks_algorithm2.PNG|thumb|500px|Рисунок 2. Особые случаи сокращения графа. <tex>(a)</tex> ребро <tex>(c, d)</tex>, которое нужно удалить, кратное. Сокращение удаляет вершины <tex>c, d</tex> из графа и соединяет <tex>a</tex> и <tex>e</tex> новым ребром. <tex>(b)</tex> ребро <tex>(c, d)</tex> инцидентно двум двойным рёбрам <tex>(a, c)</tex> и <tex>(d, e)</tex>. Сокращение удаляет вершины <tex>c, d</tex> и добавляет новое кратное ребро <tex>(a, e)</tex>. <tex>(c)</tex> Ребро <tex>(c, d)</tex> инцидентно одному ребру <tex>(d, e)</tex>. Сокращение удаляет вершины <tex>c, d</tex> и добавляет два новых ребра <tex>(a, e)</tex> и <tex>(b, e)</tex>. <tex>(d)</tex> Ребро <tex>(c, d)</tex> тройной кратности. Сокращение удаляет вершины <tex>c, d</tex>. ]] |
| + | |} | ||
| + | |||
| + | {|align="center" | ||
| + | |-valign="center" | ||
| + | |[[Файл:Frinks_algorithm3.PNG|thumb|500px|Рисунок 3. Все возможные соединения двусвязных компонент графа <tex>G[V - \{c,d\}]</tex>. <tex>(a)</tex> Компонента <tex>A</tex> соединена с компонентой <tex>E</tex>, компонента <tex>B</tex> соединена с компонентой <tex>F</tex>. <tex>(b)</tex> Компонента <tex>E</tex> соединена с компонентами <tex>A, B, F</tex>. <tex>(c)</tex> Компонента <tex>A</tex> соединена с компонентами <tex>B, E</tex>, компонента <tex>E</tex> соединена с компонентой <tex>F</tex>. ]] | ||
| + | |[[Файл:Frinks_algorithm4.PNG|thumb|500px|Рисунок 4. Возможные соединения двусвязный компонент <tex>A, B, E, F</tex> после удаления ребра <tex>(c, d)</tex> и добавления рёбер <tex>(a, f)</tex> и <tex>(b, e)</tex>.]] | ||
|} | |} | ||
| + | |||
| + | ==Алгоритм поиска совершенного паросочетания (Frink's algorithm)== | ||
| + | Будем сокращать данный граф <tex>G</tex> вышеизложенным способом (на каждой итерации можем выбирать любое ребро) пока не удалим все вершины. | ||
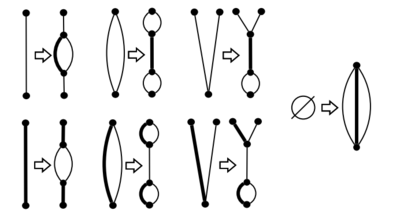
| + | Когда все вершины закончились, создадим пустое совершенное паросочетание <tex>M</tex> и начнём обратный процесс для всех сокращений, то есть будем восстанавливать граф (начиная с последних удалённых вершин). Каждый такой шаг будет приводить к одному из четырёх базовых случаев, представленных в рисунке <tex>5</tex> или к одному из специальных случаев из рисунка <tex>6</tex>. Восстановление для всех специальных случаев, а так же для первых трёх базовых выполняется по строгому алгоритму, т.е. разрешимо за <tex>O(1)</tex>. Единственный проблемный случай, когда оба ребра принадлежат совершенному паросочетанию. В этой ситуации необходимо найти альтернативный цикл, содержащий как минимум одно из этих рёбер и обновить паросочетание с этим циклом. Эти действия сводят четвёртый базовый случай к одному из первых трёх. | ||
| + | |||
{|align="center" | {|align="center" | ||
|-valign="center" | |-valign="center" | ||
| − | |[[Файл: | + | |[[Файл:Frinks_algorithm5.PNG|thumb|400px|Рисунок 5. Базовые случаи восстановления графа.]] |
| − | |[[Файл: | + | |[[Файл:Frinks_algorithm6.PNG|thumb|400px|Рисунок 6. Особые случаи восстановления графа.]] |
|} | |} | ||
| + | ==Псевдокод алгоритма Фринка== | ||
| + | *<tex>G</tex> {{---}} двусвязный кубический граф, | ||
| + | *<tex>M</tex> {{---}} совершенное паросочетание <tex>G</tex>, | ||
| + | *функция <tex>\mathtt{bridgeless}</tex> возвращает <tex>true</tex> если у графа нет моста или <tex>false</tex> в противном случае, | ||
| + | *функция <tex>\mathtt{alternatingCycle}</tex> принимает три параметра: граф, совершенное паросочетание и ребро. Возвращает альтернативный цикл, включающий в себя данное ребро и обновляет совершенное паросочетание, | ||
| + | *функция <tex>\mathtt{reductions}</tex> сокращает граф, | ||
| + | *функция <tex>\mathtt{simpleReversion}</tex> восстанавливает граф, | ||
| + | *функция <tex>\mathtt{reductedGraph}</tex> принимает три параметра: граф, удаляемые вершины, добавляемые рёбра. Возвращает новый граф, у которого удалены выбранные вершины, вместе c инцидентными рёбрами и добавлены другие рёбра, переданные в параметрах. При этом исходный граф не меняется. | ||
| + | |||
| + | '''function''' frinkMatching<tex>(G)</tex>: | ||
| + | '''if''' <tex>|V| = 0</tex> | ||
| + | '''return''' <tex>\varnothing</tex> | ||
| + | <tex>v - w = E[0]</tex> | ||
| + | <tex>R = </tex> reductions<tex>(G, v - w)</tex> | ||
| + | '''if''' bridgeless<tex>(</tex>reductedGraph<tex>(G, \{v, w\}, R[0]))</tex> | ||
| + | <tex>r = R[0]</tex> | ||
| + | '''else''' | ||
| + | <tex>r = R[1]</tex> | ||
| + | <tex>M =</tex> frinkMatching<tex>(</tex>reductedGraph<tex>(G,\{v, w\}, r))</tex> | ||
| + | '''if''' <tex>|r \cap M| = 2 </tex> | ||
| + | <tex>C =</tex> alternatingCycle<tex>(G, M, r[0])</tex> | ||
| + | <tex>M = M \oplus C</tex> | ||
| + | <tex>M = (M - r)\ \cup </tex> simpleReversion<tex>(G, v, w, r, M)</tex> | ||
| + | '''return''' <tex>M</tex> | ||
| + | |||
| + | ==Время работы алгоритма Фринка== | ||
| + | Операция сокращения должна на каждом шаге проверять граф на наличие мостов за <tex>O(n)</tex>, кроме того, при возникновении четвёртого базового случая требуется найти альтернативный цикл за <tex>O(n)</tex>. В алгоритме <tex>O(n)</tex> операций сокращения и восстановления графа, причем каждая из этих операций требует <tex>O(n)</tex> времени. Таким образом, весь этот алгоритм исполняется за время <tex>O(n^2)</tex>. | ||
| + | |||
| + | ==См. также== | ||
| + | |||
| + | * [[Использование обхода в глубину для поиска цикла]] | ||
| + | * [[Использование обхода в глубину для поиска мостов]] | ||
| + | * [[Паросочетания: основные определения, теорема о максимальном паросочетании и дополняющих цепях]] | ||
| + | |||
| + | == Источники информации == | ||
| + | * [https://www.lektorium.tv/course/22771 Лекториум {{---}} Дополнительные главы теории паросочетаний] | ||
| + | * [https://ru.wikipedia.org/wiki/%D0%9A%D1%83%D0%B1%D0%B8%D1%87%D0%B5%D1%81%D0%BA%D0%B8%D0%B9_%D0%B3%D1%80%D0%B0%D1%84 Wikipedia {{---}} Кубический граф] | ||
| + | * Piotr Stanczyk {{---}} THEORY AND PRACTICE OF COMPUTING MAXIMUM MATCHINGS IN GRAPHS стр. 21-28. | ||
| + | * Карпов В. Д. - Теория графов, стр 42 | ||
| − | + | [[Категория: Алгоритмы и структуры данных]] | |
| − | + | [[Категория: Задача о паросочетании]] | |
| − | |||
Текущая версия на 19:31, 4 сентября 2022
Содержание
Лемма о сравнимости по модулю 2
| Лемма: |
Пусть — -регулярный граф, , нечётно, — число рёбер, соединяющих вершины множества с вершинами из . Тогда |
| Доказательство: |
|
, где — количество рёбер, соединяющих вершину из с другой вершиной из . тогда . чётно, поэтому . Так как нечётно, . |
Теорема Петерсона (Petersen)
| Определение: |
| Кубический граф (англ. Cubic graph) — граф, в котором все вершины имеют степень три. Другими словами, кубический граф является -регулярным. |
| Теорема (Петерсон): |
| Доказательство: |
|
Предположим, что совершенного паросочетания в нет, тогда можно выбрать множество Татта . Пусть — все нечётные компоненты связности графа . — количество ребёр , связывающих вершины с вершинами . По предыдущей лемме, все нечётны. Так как не более чем два ребра графа — мосты, то не более, чем два числа из равны , остальные числа не менее . Так как — множество Татта, то . Так как количество вершин кубического графа чётно, мы имеем , следовательно, . Тогда , что, очевидно, невозможно. Найдено противоречие, следовательно, множество Татта выбрать невозможно, следовательно, в есть совершенное паросочетание. |
Заметим, что утверждение теоремы не может быть усилено до большего числа мостов, так как для случая с тремя мостами существует контрпример.
Теорема Фринка (Frink)
| Теорема (Фринк): |
Пусть — двусвязный кубический граф.
Возьмём ребро . Пусть вершины и смежны с вершиной , а вершины и смежны с вершиной (рисунок ). Как минимум одно из двух сокращений графа , состоящее из удаления вершин и пересоединения вершин рёбрами или (рисунок , рисунок ) сохранит двусвязность графа. |
| Доказательство: |
|
Обозначим компоненты графа как , которые содержат вершины соответственно. Так как не имеет мостов (соответственно не является мостом) должно существовать ребро, соединяющее одну из компонент или , с одной из компонент или . Без потери общности предположим, что соединено с . Заметим, что рёбра так же не являются мостами, значит возможны три случая (с учётом изоморфизма) (рисунок ):
Во всех трёх случаях если расширить рёбрами (получим граф ), добавленные рёбра будут лежать на некотором цикле в (рисунок ). Так же для любой пары вершин существует цикл в , содержащий данные вершины. Чтобы доказать, что двусвязен, нужно показать, что каждое ребро из лежит на некотором цикле в . Пусть цикл в содержит (такой цикл существует, так как двусвязен). Если не проходит через вершины тогда так же является циклом в , иначе построим цикл графа из следующим образом:
|
Алгоритм поиска совершенного паросочетания (Frink's algorithm)
Будем сокращать данный граф вышеизложенным способом (на каждой итерации можем выбирать любое ребро) пока не удалим все вершины. Когда все вершины закончились, создадим пустое совершенное паросочетание и начнём обратный процесс для всех сокращений, то есть будем восстанавливать граф (начиная с последних удалённых вершин). Каждый такой шаг будет приводить к одному из четырёх базовых случаев, представленных в рисунке или к одному из специальных случаев из рисунка . Восстановление для всех специальных случаев, а так же для первых трёх базовых выполняется по строгому алгоритму, т.е. разрешимо за . Единственный проблемный случай, когда оба ребра принадлежат совершенному паросочетанию. В этой ситуации необходимо найти альтернативный цикл, содержащий как минимум одно из этих рёбер и обновить паросочетание с этим циклом. Эти действия сводят четвёртый базовый случай к одному из первых трёх.
Псевдокод алгоритма Фринка
- — двусвязный кубический граф,
- — совершенное паросочетание ,
- функция возвращает если у графа нет моста или в противном случае,
- функция принимает три параметра: граф, совершенное паросочетание и ребро. Возвращает альтернативный цикл, включающий в себя данное ребро и обновляет совершенное паросочетание,
- функция сокращает граф,
- функция восстанавливает граф,
- функция принимает три параметра: граф, удаляемые вершины, добавляемые рёбра. Возвращает новый граф, у которого удалены выбранные вершины, вместе c инцидентными рёбрами и добавлены другие рёбра, переданные в параметрах. При этом исходный граф не меняется.
function frinkMatching: if return reductions if bridgelessreductedGraph else frinkMatchingreductedGraph if alternatingCycle simpleReversion return
Время работы алгоритма Фринка
Операция сокращения должна на каждом шаге проверять граф на наличие мостов за , кроме того, при возникновении четвёртого базового случая требуется найти альтернативный цикл за . В алгоритме операций сокращения и восстановления графа, причем каждая из этих операций требует времени. Таким образом, весь этот алгоритм исполняется за время .
См. также
- Использование обхода в глубину для поиска цикла
- Использование обхода в глубину для поиска мостов
- Паросочетания: основные определения, теорема о максимальном паросочетании и дополняющих цепях
Источники информации
- Лекториум — Дополнительные главы теории паросочетаний
- Wikipedia — Кубический граф
- Piotr Stanczyk — THEORY AND PRACTICE OF COMPUTING MAXIMUM MATCHINGS IN GRAPHS стр. 21-28.
- Карпов В. Д. - Теория графов, стр 42