Алгоритм Манакера — различия между версиями
(→Оценка сложности) |
м (rollbackEdits.php mass rollback) |
||
| (не показано 37 промежуточных версий 8 участников) | |||
| Строка 1: | Строка 1: | ||
{{Шаблон:Задача | {{Шаблон:Задача | ||
|definition = | |definition = | ||
| − | Пусть дана строка <tex>s</tex>. Требуется найти <tex> | + | Пусть дана строка <tex>s</tex>. Требуется найти количество подстрок <tex>s</tex>, являющиеся палиндромами. Более формально, все такие пары <tex>(i, j)</tex>, что <tex>s[i \ldots j]</tex> — [[Основные_определения,_связанные_со_строками#palindrome | палиндром]]. |
}} | }} | ||
| + | |||
| + | ==Уточнение постановки== | ||
| + | Легко увидеть, что таких подстрок в худшем случае будет <tex>n^2</tex>. Значит, нужно найти компактный способ хранения информации о них. Пусть <tex>d_1[i]</tex> — количество палиндромов нечётной длины с центром в позиции <tex>i</tex>, а <tex>d_2[i]</tex> — аналогичная величина для палиндромов чётной длины. Далее научимся вычислять значения этих массивов. | ||
== Наивный алгоритм == | == Наивный алгоритм == | ||
| − | ===Идея=== | + | === Идея === |
| − | + | Рассмотрим сначала задачу поиска палиндромов нечётной длины. Центром строки нечётной длины назовём символ под индексом <tex>\left\lfloor \dfrac{|t|}{2}\right\rfloor</tex>. Для каждой позиции в строке <tex>s</tex> найдем длину наибольшего палиндрома с центром в этой позиции. Очевидно, что если строка <tex>t</tex> является палиндромом, то строка полученная вычеркиванием первого и последнего символа из <tex>t</tex> также является палиндромом, поэтому длину палиндрома можно искать [[Целочисленный_двоичный_поиск | бинарным поиском]]. Проверить совпадение левой и правой половины можно выполнить за <tex>O(1)</tex>, используя метод хеширования. | |
| − | + | ||
| − | + | Для палиндромов чётной длины алгоритм такой же. Центр строки чётной длины {{---}} некий мнимый элемент между <tex>\dfrac{|t|}{2} - 1</tex> и <tex>\dfrac{|t|}{2}</tex>. Только требуется проверять вторую строку со сдвигом на единицу. Следует заметить, что мы не посчитаем никакой палиндром дважды из-за четности-нечетности длин палиндромов. | |
| − | + | ||
| − | + | === Псевдокод === | |
| − | + | '''int''' binarySearch(s : '''string''', center, shift : '''int'''): | |
| − | + | ''<font color=green>//shift = 0 при поиске палиндрома нечётной длины, иначе shift = 1</font>'' | |
| − | + | '''int''' l = -1, r = min(center, s.length - center + shift), m = 0 | |
| − | + | '''while''' r - l != 1 | |
| − | + | m = l + (r - l) / 2 | |
| − | + | ''<font color=green>//reversed_hash возвращает хэш развернутой строки s</font>'' | |
| + | '''if''' hash(s[center - m..center]) == reversed_hash(s[center + shift..center + shift + m]) | ||
| + | l = m | ||
| + | '''else''' | ||
| + | r = m | ||
| + | '''return''' r | ||
| + | |||
| + | '''int''' palindromesCount(s : '''string'''): | ||
| + | '''int''' ans = 0 | ||
| + | '''for''' i = 0 '''to''' s.length | ||
| + | ans += binarySearch(s, i, 0) + binarySearch(s, i, 1) | ||
| + | '''return''' ans | ||
| + | |||
| + | === Время работы === | ||
| + | Изначальный подсчет хешей производится за <tex>O(|s|)</tex>. Каждая итерация будет выполняться за <tex>O(\log(|s|))</tex>, всего итераций {{---}} <tex>|s|</tex>. Итоговое время работы алгоритма <tex>O(|s|+|s|\cdot \log(|s|)) = O(|s|\cdot \log(|s|))</tex>. | ||
| + | |||
| + | === Избавление от коллизий === | ||
| + | У хешей есть один недостаток {{---}} коллизии: можно подобрать входные данные так, что хеши разных строк будут совпадать. Абсолютно точно проверить две подстроки на совпадение можно с помощью [[Суффиксный массив | суффиксного массива]], но с дополнительной памятью <tex>O(|s|\cdot \log(|s|))</tex>. Для этого построим суффиксный массив для строки <tex>s + \# + reverse(s)</tex>, при этом сохраним промежуточные результаты классов эквивалентности <tex>c</tex>. Пусть нам требуется проверить на совпадение подстроки <tex>s[i \ldots i + l]</tex> и <tex>s[j \ldots j + l]</tex>. Разобьем каждую нашу строку на две пересекающиеся подстроки длиной <tex>2^k</tex>, где <tex>k = \lfloor \log{l} \rfloor</tex>. Тогда наши строки совпадают, если <tex>c[k][i] = c[k][j]</tex> и <tex>c[k][i + l - 2^k] = c[k][j + l - 2^k]</tex>. | ||
| + | |||
| + | Итоговая асимптотика алгоритма: предподсчет за построение суффиксного массива и <tex>O(\log(|s|))</tex> на запрос, если предподсчитать все <tex>k</tex>, то <tex>O(1)</tex>. | ||
| + | |||
==Алгоритм Манакера== | ==Алгоритм Манакера== | ||
===Идея=== | ===Идея=== | ||
Алгоритм, который будет описан далее, отличается от наивного тем, что использует значения, посчитанные ранее. | Алгоритм, который будет описан далее, отличается от наивного тем, что использует значения, посчитанные ранее. | ||
| − | Будем поддерживать границы самого правого из найденных палиндромов — <tex>[l; r]</tex>. Итак, пусть мы хотим вычислить <tex> | + | Будем поддерживать границы самого правого из найденных палиндромов — <tex>[l; r]</tex>. Итак, пусть мы хотим вычислить <tex>d_1[i]</tex> — т.е. длину наибольшего палиндрома с центром в позиции <tex>i</tex>. При этом все предыдущие значения в массиве <tex>d</tex> уже посчитаны. Возможны два случая: |
# <tex>i > r</tex>, т.е. текущая позиция не попадает в границы самого правого из найденных палиндромов. Тогда просто запустим наивный алгоритм для позиции <tex>i</tex>. | # <tex>i > r</tex>, т.е. текущая позиция не попадает в границы самого правого из найденных палиндромов. Тогда просто запустим наивный алгоритм для позиции <tex>i</tex>. | ||
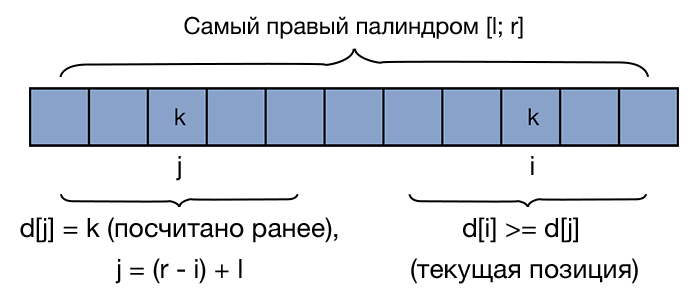
| − | # <tex>i \leqslant r</tex>. Тогда попробуем воспользоваться значениями, посчитанным ранее. Отразим нашу текущую позицию внутри палиндрома <tex>[l;r] : j = (r - i) + l</tex>. Поскольку <tex>i</tex> и <tex>j</tex> — симметричные позиции, то мы можем утверждать, <tex> | + | # <tex>i \leqslant r</tex>. Тогда попробуем воспользоваться значениями, посчитанным ранее. Отразим нашу текущую позицию внутри палиндрома <tex>[l;r] : j = (r - i) + l</tex>. Поскольку <tex>i</tex> и <tex>j</tex> — симметричные позиции, то если <tex>d_1[j] = k</tex>, мы можем утверждать, что и <tex>d_1[i] = k</tex>. Это объясняется тем, что палиндром симметричен относительно своей центральной позиции. Т.е. если имеем некоторый палиндром длины <tex>k</tex> с центром в позиции <tex>l \leqslant i \leqslant r</tex>, то в позиции <tex>j</tex>, симметричной <tex>i</tex> относительно отрезка <tex>[l; r]</tex> тоже может находиться палиндром длины <tex>k</tex>. Это можно лучше понять, посмотрев на рисунок. Снизу фигурными скобками обозначены равные подстроки. Однако стоит не забыть про один граничный случай: что если <tex>i + d_1[j] - 1</tex> выходит за границы самого правого палиндрома? Так как информации о том, что происходит за границами этого палиндрома у нас нет (а значит мы не можем утверждать, что симметрия сохраняется), то необходимо ограничить значение <tex>d_1[i]</tex> следующим образом: <tex>d_1[i] = \min(r - i, d_1[j])</tex>. После этого запустим наивный алгоритм, который будет увеличивать значение <tex>d_1[i]</tex>, пока это возможно. |
| − | После каждого шага важно не забывать обновлять значения <tex>[l;r]</tex> | + | После каждого шага важно не забывать обновлять значения <tex>[l;r]</tex>. |
| − | Заметим, что массив <tex> | + | Заметим, что массив <tex>d_2</tex> считается аналогичным образом, нужно лишь немного изменить индексы. |
[[Файл:Манакер.png]] | [[Файл:Манакер.png]] | ||
===Псевдокод=== | ===Псевдокод=== | ||
| − | Приведем код, который вычисляет значения массива <tex> | + | Приведем код, который вычисляет значения массива <tex>d_1</tex>: |
<font color=green>// <tex>s</tex> {{---}} исходная строка</font> | <font color=green>// <tex>s</tex> {{---}} исходная строка</font> | ||
| − | '''int''' l = 0 | + | '''int[]''' calculate1('''string''' s): |
| − | + | '''int''' l = 0 | |
| − | + | '''int''' r = -1 | |
| − | + | '''for''' i = 1 '''to''' n | |
| − | + | '''int''' k = 0 | |
| − | + | '''if''' i <= r | |
| − | + | k = min(r - i, <tex>d_1</tex>[r - i + l]) | |
| − | + | '''while''' i + k + 1 <= n '''and''' i - k - 1 > 0 '''and''' s[i + k + 1] == s[i - k - 1] | |
| − | + | k++ | |
| − | + | <tex>d_1</tex>[i] = k | |
| − | + | '''if''' i + k > r | |
| − | + | l = i - k | |
| + | r = i + k | ||
| + | '''return''' <tex>d_1</tex> | ||
| − | Вычисление значений массива <tex> | + | Вычисление значений массива <tex>d_2</tex>: |
<font color=green>// <tex>s</tex> {{---}} исходная строка</font> | <font color=green>// <tex>s</tex> {{---}} исходная строка</font> | ||
| − | '''int''' l = 0 | + | '''int[]''' calculate2('''string''' s): |
| − | + | '''int''' l = 0 | |
| − | + | '''int''' r = -1 | |
| − | + | '''for''' i = 1 '''to''' n | |
| − | + | '''int''' k = 0 | |
| − | + | '''if''' i <= r | |
| − | + | k = min(r - i + 1, <tex>d_2</tex>[r - i + l + 1]) | |
| − | + | '''while''' i + k <= n '''and''' i - k - 1 > 0 '''and''' s[i + k] == s[i - k - 1] | |
| − | + | k++ | |
| − | + | <tex>d_2</tex>[i] = k | |
| − | + | '''if''' i + k - 1 > r | |
| − | + | l = i - k | |
| + | r = i + k - 1 | ||
| + | '''return''' <tex>d_2</tex> | ||
===Оценка сложности=== | ===Оценка сложности=== | ||
Внешний цикл в приведенном алгоритме выполняется ровно <tex>n</tex> раз, где <tex>n</tex> — длина строки. Попытаемся понять, сколько раз будет выполнен внутренний цикл, ответственный за наивный подсчет значений. Заметим, что каждая итерация вложенного цикла приводит к увеличению <tex>r</tex> на <tex>1</tex>. Действительно, возможны следующие случаи: | Внешний цикл в приведенном алгоритме выполняется ровно <tex>n</tex> раз, где <tex>n</tex> — длина строки. Попытаемся понять, сколько раз будет выполнен внутренний цикл, ответственный за наивный подсчет значений. Заметим, что каждая итерация вложенного цикла приводит к увеличению <tex>r</tex> на <tex>1</tex>. Действительно, возможны следующие случаи: | ||
| − | # <tex>i > r</tex>, т.е. сразу будет запущен наивный алгоритм и каждая его итерация будет увеличивать значение <tex>r</tex> хотя бы на <tex>1</tex> | + | # <tex>i > r</tex>, т.е. сразу будет запущен наивный алгоритм и каждая его итерация будет увеличивать значение <tex>r</tex> хотя бы на <tex>1</tex>. |
# <tex>i \leqslant r</tex>. Здесь опять два случая: | # <tex>i \leqslant r</tex>. Здесь опять два случая: | ||
| − | ## <tex>i + d[j] - 1 \leqslant r</tex>, но тогда, очевидно, ни одной итерации вложенного цикла выполнено не будет | + | ## <tex>i + d[j] - 1 \leqslant r</tex>, но тогда, очевидно, ни одной итерации вложенного цикла выполнено не будет. |
## <tex>i + d[j] - 1 > r</tex>, тогда каждая итерация вложенного цикла приведет к увеличению <tex>r</tex> хотя бы на <tex>1</tex>. | ## <tex>i + d[j] - 1 > r</tex>, тогда каждая итерация вложенного цикла приведет к увеличению <tex>r</tex> хотя бы на <tex>1</tex>. | ||
| − | Т.к. значение <tex>r</tex> не может увеличиваться более <tex>n</tex> раз, то описанный выше алгоритм работает за | + | Т.к. значение <tex>r</tex> не может увеличиваться более <tex>n</tex> раз, то описанный выше алгоритм работает за время <tex>O(n)</tex>. |
== См. также == | == См. также == | ||
| − | * [[Z | + | * [[Префикс-функция]] |
| + | * [[Z-функция]] | ||
| + | * [[Суффиксный массив]] | ||
| + | * [[Поиск наибольшей общей подстроки двух строк с использованием хеширования]] | ||
== Источники информации == | == Источники информации == | ||
| − | *[http://e-maxx.ru/algo/palindromes_count MAXimal :: algo :: Нахождение всех подпалиндромов] | + | * [http://e-maxx.ru/algo/palindromes_count MAXimal :: algo :: Нахождение всех подпалиндромов] |
| − | + | * [[wikipedia:ru:Поиск_длиннейшей_подстроки-палиндрома| Википедия — Поиск длиннейшей подстроки-палиндрома]] | |
| + | * [https://habrahabr.ru/post/276195/ Алгоритмы для поиска палиндромов — Хабр] | ||
| + | * [http://e-maxx.ru/algo/suffix_array#5 MAXimal :: algo :: Суффиксный массив] | ||
[[Категория: Алгоритмы и структуры данных]] | [[Категория: Алгоритмы и структуры данных]] | ||
| + | [[Категория: Основные определения. Простые комбинаторные свойства слов]] | ||
Текущая версия на 19:29, 4 сентября 2022
| Задача: |
| Пусть дана строка . Требуется найти количество подстрок , являющиеся палиндромами. Более формально, все такие пары , что — палиндром. |
Уточнение постановки
Легко увидеть, что таких подстрок в худшем случае будет . Значит, нужно найти компактный способ хранения информации о них. Пусть — количество палиндромов нечётной длины с центром в позиции , а — аналогичная величина для палиндромов чётной длины. Далее научимся вычислять значения этих массивов.
Наивный алгоритм
Идея
Рассмотрим сначала задачу поиска палиндромов нечётной длины. Центром строки нечётной длины назовём символ под индексом . Для каждой позиции в строке найдем длину наибольшего палиндрома с центром в этой позиции. Очевидно, что если строка является палиндромом, то строка полученная вычеркиванием первого и последнего символа из также является палиндромом, поэтому длину палиндрома можно искать бинарным поиском. Проверить совпадение левой и правой половины можно выполнить за , используя метод хеширования.
Для палиндромов чётной длины алгоритм такой же. Центр строки чётной длины — некий мнимый элемент между и . Только требуется проверять вторую строку со сдвигом на единицу. Следует заметить, что мы не посчитаем никакой палиндром дважды из-за четности-нечетности длин палиндромов.
Псевдокод
int binarySearch(s : string, center, shift : int):
//shift = 0 при поиске палиндрома нечётной длины, иначе shift = 1
int l = -1, r = min(center, s.length - center + shift), m = 0
while r - l != 1
m = l + (r - l) / 2
//reversed_hash возвращает хэш развернутой строки s
if hash(s[center - m..center]) == reversed_hash(s[center + shift..center + shift + m])
l = m
else
r = m
return r
int palindromesCount(s : string):
int ans = 0
for i = 0 to s.length
ans += binarySearch(s, i, 0) + binarySearch(s, i, 1)
return ans
Время работы
Изначальный подсчет хешей производится за . Каждая итерация будет выполняться за , всего итераций — . Итоговое время работы алгоритма .
Избавление от коллизий
У хешей есть один недостаток — коллизии: можно подобрать входные данные так, что хеши разных строк будут совпадать. Абсолютно точно проверить две подстроки на совпадение можно с помощью суффиксного массива, но с дополнительной памятью . Для этого построим суффиксный массив для строки , при этом сохраним промежуточные результаты классов эквивалентности . Пусть нам требуется проверить на совпадение подстроки и . Разобьем каждую нашу строку на две пересекающиеся подстроки длиной , где . Тогда наши строки совпадают, если и .
Итоговая асимптотика алгоритма: предподсчет за построение суффиксного массива и на запрос, если предподсчитать все , то .
Алгоритм Манакера
Идея
Алгоритм, который будет описан далее, отличается от наивного тем, что использует значения, посчитанные ранее. Будем поддерживать границы самого правого из найденных палиндромов — . Итак, пусть мы хотим вычислить — т.е. длину наибольшего палиндрома с центром в позиции . При этом все предыдущие значения в массиве уже посчитаны. Возможны два случая:
- , т.е. текущая позиция не попадает в границы самого правого из найденных палиндромов. Тогда просто запустим наивный алгоритм для позиции .
- . Тогда попробуем воспользоваться значениями, посчитанным ранее. Отразим нашу текущую позицию внутри палиндрома . Поскольку и — симметричные позиции, то если , мы можем утверждать, что и . Это объясняется тем, что палиндром симметричен относительно своей центральной позиции. Т.е. если имеем некоторый палиндром длины с центром в позиции , то в позиции , симметричной относительно отрезка тоже может находиться палиндром длины . Это можно лучше понять, посмотрев на рисунок. Снизу фигурными скобками обозначены равные подстроки. Однако стоит не забыть про один граничный случай: что если выходит за границы самого правого палиндрома? Так как информации о том, что происходит за границами этого палиндрома у нас нет (а значит мы не можем утверждать, что симметрия сохраняется), то необходимо ограничить значение следующим образом: . После этого запустим наивный алгоритм, который будет увеличивать значение , пока это возможно.
После каждого шага важно не забывать обновлять значения .
Заметим, что массив считается аналогичным образом, нужно лишь немного изменить индексы.
Псевдокод
Приведем код, который вычисляет значения массива :
// — исходная строка int[] calculate1(string s): int l = 0 int r = -1 for i = 1 to n int k = 0 if i <= r k = min(r - i, [r - i + l]) while i + k + 1 <= n and i - k - 1 > 0 and s[i + k + 1] == s[i - k - 1] k++ [i] = k if i + k > r l = i - k r = i + k return
Вычисление значений массива :
// — исходная строка int[] calculate2(string s): int l = 0 int r = -1 for i = 1 to n int k = 0 if i <= r k = min(r - i + 1, [r - i + l + 1]) while i + k <= n and i - k - 1 > 0 and s[i + k] == s[i - k - 1] k++ [i] = k if i + k - 1 > r l = i - k r = i + k - 1 return
Оценка сложности
Внешний цикл в приведенном алгоритме выполняется ровно раз, где — длина строки. Попытаемся понять, сколько раз будет выполнен внутренний цикл, ответственный за наивный подсчет значений. Заметим, что каждая итерация вложенного цикла приводит к увеличению на . Действительно, возможны следующие случаи:
- , т.е. сразу будет запущен наивный алгоритм и каждая его итерация будет увеличивать значение хотя бы на .
- . Здесь опять два случая:
- , но тогда, очевидно, ни одной итерации вложенного цикла выполнено не будет.
- , тогда каждая итерация вложенного цикла приведет к увеличению хотя бы на .
Т.к. значение не может увеличиваться более раз, то описанный выше алгоритм работает за время .