Бор — различия между версиями
ExileHell (обсуждение | вклад) (→Построение) |
м (rollbackEdits.php mass rollback) |
||
| (не показано 98 промежуточных версий 4 участников) | |||
| Строка 1: | Строка 1: | ||
| − | '''Бор''' (англ. ''trie'', ''луч'', ''нагруженное дерево'') | + | '''Бор''' (англ. ''trie'', ''луч'', ''нагруженное дерево'') {{---}} структура данных для хранения набора строк, представляющая из себя [[Дерево, эквивалентные определения | подвешенное дерево]] с символами на [[Основные определения теории графов | рёбрах]]. Строки получаются последовательной записью всех символов, хранящихся на [[Основные определения теории графов | рёбрах]] между корнем бора и терминальной вершиной. Размер бора линейно |
зависит от суммы длин всех строк, а поиск в бору занимает время, пропорциональное длине образца. | зависит от суммы длин всех строк, а поиск в бору занимает время, пропорциональное длине образца. | ||
| Строка 7: | Строка 7: | ||
==Построение== | ==Построение== | ||
| − | + | ===Обозначения=== | |
| + | Введем следующие обозначения: | ||
| + | *<tex>\Sigma</tex> {{---}} используемый алфавит; | ||
| + | *<tex>P = \{P_1,\ldots,P_k\} </tex> {{---}} набор строк над <tex>\Sigma</tex>, называемый словарём; | ||
| + | *<tex>n = \sum_{i=1}^{k}\limits |P_i|</tex> {{---}} сумма длин строк. | ||
| − | + | Бор храним как набор вершин, у каждой из которых есть метка, обозначающая, является ли вершина терминальной и указатели (рёбра) на другие вершины или на ''NULL''. | |
| + | '''struct''' vertex: | ||
| + | '''vertex''' next[<tex>| \Sigma |</tex>] | ||
| + | '''bool''' isTerminal | ||
| + | |||
| + | ===Алгоритм=== | ||
Непосредственно построение: | Непосредственно построение: | ||
| − | + | *Начало. | |
| − | + | *'''Шаг 1.''' Создадим [[Дерево, эквивалентные определения | дерево]] из одной вершины (в нашем случае корня). | |
| − | + | *'''Шаг 2.''' Добавление элементов в дерево. | |
| − | + | **Добавляем шаблоны <tex>P_i</tex> один за другим. Следуем из корня по [[Основные определения теории графов | рёбрам]], отмеченным буквами из <tex>P_i</tex>, пока возможно. | |
| − | + | **Если <tex>P_i</tex> заканчивается в <tex>v</tex>, сохраняем идентификатор <tex>P_i</tex> (например, <tex>i</tex>) в <tex>v</tex> и отмечаем вершину <tex>v</tex> как терминальную. | |
| + | **Если [[Основные определения теории графов | ребра]], отмеченного очередной буквой <tex>P_i</tex> нет, то создаем новое ребро и вершину для символа строки <tex>P_i</tex>. | ||
| + | *Конец. | ||
| + | Построение занимает, очевидно, <tex>O(|P_1| + \ldots + |P_k|) = O(n)</tex> времени, так как поиск буквы, по которой нужно переходить, происходит за <tex>O(1)</tex>. | ||
| − | + | Поскольку на каждую вершину приходится <tex>O(| \Sigma |)</tex> памяти, то использование памяти есть <tex>O(n| \Sigma |)</tex>. | |
| − | + | ===Суффиксный бор=== | |
| + | {{main|Суффиксный бор}} | ||
| + | Бор позволяет решать задачу [[Наивный алгоритм поиска подстроки в строке | поиска подстроки в строке]], если построить его на множестве суффиксов исходной строки. | ||
| − | + | ===Цифровой бор=== | |
| + | {{main|Сверхбыстрый цифровой бор}} | ||
| − | + | ==Использование бора== | |
| − | + | ===Поиск строки в бору=== | |
| − | |||
| − | ==Поиск строки в бору== | ||
{{Задача | {{Задача | ||
|definition = | |definition = | ||
| − | Требуется найти слово в словаре. | + | Требуется найти слово <tex>S</tex> в словаре. |
}} | }} | ||
| − | + | При решении этой задачи, обход бора совершается из его корня по [[Основные определения теории графов | рёбрам]], отмеченным символами строки <tex>S</tex>, пока возможно. | |
| − | Если с последним символом <tex>S</tex> мы приходим в вершину | + | Если с последним символом <tex>S</tex> мы приходим в терминальную вершину, то <tex>S</tex> — слово из словаря. |
Если в какой-то момент [[Основные определения теории графов | ребра]], отмеченного нужным символом, не находится, то строки <tex>S</tex> в словаре нет. | Если в какой-то момент [[Основные определения теории графов | ребра]], отмеченного нужным символом, не находится, то строки <tex>S</tex> в словаре нет. | ||
Ясно, что это занимает <tex>O (|S|)</tex> времени. Таким образом, бор — это эффективный способ хранить словарь и искать в нем слова. | Ясно, что это занимает <tex>O (|S|)</tex> времени. Таким образом, бор — это эффективный способ хранить словарь и искать в нем слова. | ||
| − | ==Использование бора в качестве ассоциативного массива== | + | ===Использование бора в качестве ассоциативного массива=== |
| − | + | Благодаря тому, что бор позволяет решать задачу, описанную выше, он может выступать в качестве ассоциативного массива. Обычно, когда требуется такая структура, то используют [[Дерево поиска, наивная реализация | двоичное дерево поиска]] или [[Хеш-таблица | хеш-таблицу]]. | |
| − | + | ====Достоинства==== | |
| + | Бор объединяет некоторые преимущества этих структур данных и позволяет одновременно делать следующие операции, которые каждая из структур не может делать по отдельности. | ||
| + | |||
| + | {| class="wikitable" style="width:10cm" border=1 | ||
| + | |+ | ||
| + | | || '''Бор''' || '''Дерево''' || '''Хеш-таблица''' | ||
| + | |- | ||
| + | |-align="center" bgcolor=#FFFFFF | ||
| + | | ''Добавление элемента'' | ||
| + | | align="center" style="background: #ddffdd;" | <tex>O(|S|)</tex> | ||
| + | | align="center" style="background: #ffdddd;" |<tex>O(|S|\log k)</tex> | ||
| + | | align="center" style="background: #ddffdd;" | <tex>O(|S|)</tex> | ||
| + | |-align="center" bgcolor=#FFFFFF | ||
| + | | ''Получение всех ключей в отсортированном порядке'' | ||
| + | | align="center" style="background: #ddffdd;" | <tex>O(k)</tex> | ||
| + | | align="center" style="background: #ddffdd;" | <tex>O(k)</tex> | ||
| + | | align="center" style="background: #ffdddd;" | <tex>O(k\log k)</tex> | ||
| + | |} | ||
| + | |||
| + | ====Недостатки==== | ||
| + | Несмотря на данные достоинства у реализации ассоциативного массива в виде бора есть следующие недостатки: | ||
| + | # Бор хранит строки или символы, а это значит, что у значения ключа будет ограничение на тип (строки, символы, либо числа, представленные как строки). Чтобы это исправить, научимся приводить любой тип данных к строке. Тогда сможем хранить любой вид данных в качестве ключа. | ||
| + | #Если реализовывать ассоциативный массив на обычном боре, а ключами будут являться строки, то будет использоваться слишком много памяти (возможен, например, вариант, когда у слов нет пересечений по префиксу, тогда бор будет использовать <tex>O(n| \Sigma |)</tex> памяти). | ||
==См. также== | ==См. также== | ||
| Строка 46: | Строка 81: | ||
* [[Сжатое суффиксное дерево]] | * [[Сжатое суффиксное дерево]] | ||
* [[Алгоритм Ахо-Корасик]] | * [[Алгоритм Ахо-Корасик]] | ||
| − | |||
== Источники информации == | == Источники информации == | ||
| Строка 52: | Строка 86: | ||
*[http://e-maxx.ru/algo/aho_corasick Бор. Построение бора] | *[http://e-maxx.ru/algo/aho_corasick Бор. Построение бора] | ||
| − | + | ||
| − | |||
[[Категория: Алгоритмы и структуры данных]] | [[Категория: Алгоритмы и структуры данных]] | ||
Текущая версия на 19:17, 4 сентября 2022
Бор (англ. trie, луч, нагруженное дерево) — структура данных для хранения набора строк, представляющая из себя подвешенное дерево с символами на рёбрах. Строки получаются последовательной записью всех символов, хранящихся на рёбрах между корнем бора и терминальной вершиной. Размер бора линейно зависит от суммы длин всех строк, а поиск в бору занимает время, пропорциональное длине образца.
Содержание
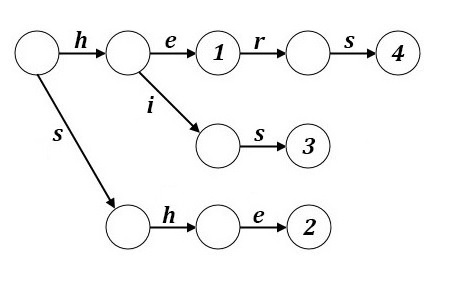
Пример
Построение
Обозначения
Введем следующие обозначения:
- — используемый алфавит;
- — набор строк над , называемый словарём;
- — сумма длин строк.
Бор храним как набор вершин, у каждой из которых есть метка, обозначающая, является ли вершина терминальной и указатели (рёбра) на другие вершины или на NULL.
struct vertex:
vertex next[]
bool isTerminal
Алгоритм
Непосредственно построение:
- Начало.
- Шаг 1. Создадим дерево из одной вершины (в нашем случае корня).
- Шаг 2. Добавление элементов в дерево.
- Конец.
Построение занимает, очевидно, времени, так как поиск буквы, по которой нужно переходить, происходит за .
Поскольку на каждую вершину приходится памяти, то использование памяти есть .
Суффиксный бор
Бор позволяет решать задачу поиска подстроки в строке, если построить его на множестве суффиксов исходной строки.
Цифровой бор
Использование бора
Поиск строки в бору
| Задача: |
| Требуется найти слово в словаре. |
При решении этой задачи, обход бора совершается из его корня по рёбрам, отмеченным символами строки , пока возможно. Если с последним символом мы приходим в терминальную вершину, то — слово из словаря. Если в какой-то момент ребра, отмеченного нужным символом, не находится, то строки в словаре нет. Ясно, что это занимает времени. Таким образом, бор — это эффективный способ хранить словарь и искать в нем слова.
Использование бора в качестве ассоциативного массива
Благодаря тому, что бор позволяет решать задачу, описанную выше, он может выступать в качестве ассоциативного массива. Обычно, когда требуется такая структура, то используют двоичное дерево поиска или хеш-таблицу.
Достоинства
Бор объединяет некоторые преимущества этих структур данных и позволяет одновременно делать следующие операции, которые каждая из структур не может делать по отдельности.
| Бор | Дерево | Хеш-таблица | |
| Добавление элемента | |||
| Получение всех ключей в отсортированном порядке |
Недостатки
Несмотря на данные достоинства у реализации ассоциативного массива в виде бора есть следующие недостатки:
- Бор хранит строки или символы, а это значит, что у значения ключа будет ограничение на тип (строки, символы, либо числа, представленные как строки). Чтобы это исправить, научимся приводить любой тип данных к строке. Тогда сможем хранить любой вид данных в качестве ключа.
- Если реализовывать ассоциативный массив на обычном боре, а ключами будут являться строки, то будет использоваться слишком много памяти (возможен, например, вариант, когда у слов нет пересечений по префиксу, тогда бор будет использовать памяти).
См. также
Источники информации
- Томас Х. Кормен, Чарльз И. Лейзерсон, Рональд Л. Ривест, Клиффорд Штайн Алгоритмы: построение и анализ — 2-е изд. — М.: «Вильямс», 2007. — ISBN 5-8489-0857-4
- Бор. Построение бора