Z-функция — различия между версиями
м (→Псевдокод) |
м (rollbackEdits.php mass rollback) |
||
| (не показаны 33 промежуточные версии 7 участников) | |||
| Строка 1: | Строка 1: | ||
{{Определение | {{Определение | ||
| − | |definition = '''Z-функция''' (англ. ''Z-function'') от строки <tex>S</tex> и позиции <tex>x</tex> — это длина максимального префикса подстроки, начинающейся с позиции <tex>x</tex> в строке <tex>S</tex>, который одновременно является и префиксом всей строки <tex>S</tex>. Более формально, <tex>Z[i](s) = \max k \mid s[i\, \ | + | |definition = '''Z-функция''' (англ. ''Z-function'') от строки <tex>S</tex> и позиции <tex>x</tex> — это длина максимального префикса подстроки, начинающейся с позиции <tex>x</tex> в строке <tex>S</tex>, который одновременно является и префиксом всей строки <tex>S</tex>. Более формально, <tex>Z[i](s) = \max k \mid s[i\, \ldots \, i + k] = s[0 \ldots k]</tex>. <!-- проинлайнил \twodots из clrscode --> |
Значение Z-функции от первой позиции не определено, поэтому его обычно приравнивают к нулю или к длине строки. | Значение Z-функции от первой позиции не определено, поэтому его обычно приравнивают к нулю или к длине строки. | ||
| Строка 46: | Строка 46: | ||
'''while''' i + zf[i] < n '''and''' s[zf[i]] == s[i + zf[i]] | '''while''' i + zf[i] < n '''and''' s[zf[i]] == s[i + zf[i]] | ||
zf[i]++ | zf[i]++ | ||
| − | '''if''' i + zf[i] > | + | '''if''' i + zf[i] > right |
left = i | left = i | ||
right = i + zf[i] | right = i + zf[i] | ||
| Строка 66: | Строка 66: | ||
==Построение строки по Z-функции== | ==Построение строки по Z-функции== | ||
{{Задача | {{Задача | ||
| − | |definition= | + | |definition= Необходимо восстановить строку по Z-функции, считая алфавит ограниченным. |
}} | }} | ||
| − | |||
===Описание алгоритма=== | ===Описание алгоритма=== | ||
| − | |||
Пусть в массиве <tex>z</tex> хранятся значения Z-функции, в <tex>s</tex> будет записан ответ. Пойдем по массиву <tex>z</tex> слева направо. | Пусть в массиве <tex>z</tex> хранятся значения Z-функции, в <tex>s</tex> будет записан ответ. Пойдем по массиву <tex>z</tex> слева направо. | ||
Нужно узнать значение <tex>s[i]</tex>. Для этого посмотрим на значение <tex>z[i]</tex>: если <tex>z[i] = 0</tex>, тогда в <tex>s[i]</tex> запишем ещё не использованный символ или последний использованный символ алфавита, если мы уже использовали все символы. Если <tex>z[i] \neq 0</tex>, то нам нужно записать префикс длины <tex>z[i]</tex> строки <tex>s</tex>. Но если при посимвольном записывании этого префикса в конец строки <tex>s</tex> мы нашли такой <tex>j</tex> (индекс последнего символа строки), что <tex>z[j]</tex> больше, чем длина оставшейся незаписанной части префикса, то мы перестаём писать этот префикс и пишем префикс длиной <tex>z[j]</tex> строки <tex>s</tex>. | Нужно узнать значение <tex>s[i]</tex>. Для этого посмотрим на значение <tex>z[i]</tex>: если <tex>z[i] = 0</tex>, тогда в <tex>s[i]</tex> запишем ещё не использованный символ или последний использованный символ алфавита, если мы уже использовали все символы. Если <tex>z[i] \neq 0</tex>, то нам нужно записать префикс длины <tex>z[i]</tex> строки <tex>s</tex>. Но если при посимвольном записывании этого префикса в конец строки <tex>s</tex> мы нашли такой <tex>j</tex> (индекс последнего символа строки), что <tex>z[j]</tex> больше, чем длина оставшейся незаписанной части префикса, то мы перестаём писать этот префикс и пишем префикс длиной <tex>z[j]</tex> строки <tex>s</tex>. | ||
| − | Для правильной работы алгоритма | + | Для правильной работы алгоритма будем считать значение <tex>z[0]</tex> равным нулю. |
| + | |||
| + | Заметим, что не всегда удастся восстановить строку с ограниченным алфавитом неподходящего размера. Например, для строки <tex>abacaba</tex> массив Z-функций будет <tex>[0, 0, 1, 0, 3, 0, 1]</tex>. Используя двоичный алфавит, мы получим строку <tex>abababa</tex>, но её массив Z-функций отличается от исходного. Ошибка восстановления строки возникла, когда закончились новые символы алфавита. | ||
| − | + | Если строить строку по некорректному массиву значений Z-функции, то мы получим какую-то строку, но массив значений Z-функций от неё будет отличаться от исходного. | |
| + | === Время работы === | ||
| + | Этот алгоритм работает за O(|S|), так как мы один раз проходим по массиву Z-функций. | ||
=== Реализация === | === Реализация === | ||
'''string''' buildFromZ(z : '''int'''[], alphabet : '''char'''[]): | '''string''' buildFromZ(z : '''int'''[], alphabet : '''char'''[]): | ||
| Строка 108: | Строка 110: | ||
Докажем, что если нам дали корректную Z-функцию, то наш алгоритм построит строку с такой же Z-функцией. | Докажем, что если нам дали корректную Z-функцию, то наш алгоритм построит строку с такой же Z-функцией. | ||
| − | Пусть <tex>z</tex> — данная Z-функция, строку <tex>s</tex> построил наш алгоритм, <tex>q</tex> — массив значений Z-функции для <tex>s</tex>. | + | Пусть <tex>z</tex> — данная Z-функция, строку <tex>s</tex> построил наш алгоритм, <tex>q</tex> — массив значений Z-функции для <tex>s</tex>. Покажем, что массивы <tex>q</tex> и <tex>z</tex> будут совпадать. |
| − | + | [[Файл: Запись_префикса.png|330px|thumb|right|Записали префикс, начинающийся в <tex>i</tex>. После пишем префикс, начинающийся в <tex>j</tex>. Этот префикс не изменит символы первого префикса.]] | |
| − | Рассмотрим | + | Рассмотрим похожий алгоритм, но с более худшей асимптотикой. Отличие будет в том, что при <tex>z[i] > 0</tex> мы будем писать префикс полностью и возвращаться в позицию <tex>i + 1</tex>. Рассмотрим каждый шаг этого алгоритма. Если <tex>z[i] = 0</tex>, то мы пишем символ, отличный от первого символа строки, поэтому <tex>q[i] = 0</tex>, а значит <tex>q[i] = z[i]</tex>. Если <tex>z[i] > 0</tex>, то при записи <tex>s[i]</tex> мы будем получать <tex>q[i] = z[i]</tex>, потому что мы переписали префикс строки. Но далее мы можем переписать этот префикс другим префиксом. Заметим, что новый префикс будет содержаться и в префиксе самой строки, поэтому пересечение двух префиксов будет состоять из одинаковых символов. Значит, префикс не будет изменяться, как и значение <tex>q[i]</tex>. Тогда массив <tex>q</tex> совпадает с <tex>z</tex>. |
| − | |||
| − | |||
| − | |||
| − | + | Покажем, что этот алгоритм эквивалентен нашему алгоритму. Когда мы пишем разные префиксы, то возможны три варианта: они не пересекаются (начало и конец одного префикса не принадлежат другому), один лежит внутри другого (начало и конец префикса принадлежит другому), они пересекаются (начало одного префикса пренадлежит другому, но конец не принадлежит). | |
| − | ==Построение Z-функции по префикс-функции== | + | * Если префиксы не пересекаются, то в алгоритме они не влияют друг на друга. |
| − | = | + | [[Файл: Префиксы1.png|400px]] |
| − | Дан массив с корректной [[Префикс-функция | префикс-функцией]] для строки <tex>s</tex> | + | * Если префикс лежит внутри другого префикса, то записав большой префикс мы запишем и малый, поэтому не нужно возвращаться к началу малого префикса. |
| + | [[Файл: Префиксы2.png|400px]] | ||
| + | * Если префиксы пересекаются, то нам нужно переписать часть префикса, который начинается раньше, и начать писать другой префикс (начало этого префикса запишет конец префикса, начинающегося раньше). Если полностью переписать префикс, начинающийся раньше, то мы не сможем восстановить префикс, который начинался раньше конца первого префикса. | ||
| + | [[Файл: Префиксы3.png|400px]] | ||
| + | |||
| + | Таким образом, алгоритмы эквивалентны и наш алгоритм тоже корректен. | ||
| + | |||
| + | ==Построение Z-функции по префикс-функции== | ||
| + | |||
| + | {{Задача | ||
| + | |definition= Дан массив с корректной [[Префикс-функция | префикс-функцией]] для строки <tex>s</tex>. Требуется получить массив с Z-функцией для строки <tex>s</tex>. | ||
| + | }}[[Файл:Case one.png|300px|thumb|right|'''Случай первый''']] | ||
| + | [[Файл:Case two.png|300px|thumb|right|'''Случай второй''']] | ||
| + | [[Файл:Case three.png|300px|thumb|right|'''Случай третий''']] | ||
| + | |||
| + | <br> | ||
===Описание алгоритма=== | ===Описание алгоритма=== | ||
| + | <br> | ||
| + | Пусть префикс функция хранится в массиве <tex>P[0 \ldots n - 1]</tex>. Z-функцию будем записывать в массив <tex>Z[0 \ldots n-1]</tex>. Заметим, что если <tex>P[i]>0</tex>, то мы можем заявить, что <tex>Z[i-P[i]+1]</tex> будет не меньше, чем <tex>P[i]</tex>. | ||
| + | <br> | ||
| + | <br> | ||
| + | Так же заметим, что после такого прохода в <tex>Z[1]</tex> будет максимальное возможное значение. Далее будем поддерживать инвариант: в <tex>Z[i]</tex> будет максимальное возможное значение. | ||
| + | <br> | ||
| + | <br> | ||
| + | Пусть в <tex>Z[i] = z > 0</tex>, рассмотрю <tex>j<z</tex>, <tex>Z[j]=k</tex> и <tex>Z[i+j]=k_1</tex>. Пусть <tex>b_1=s[0 \ldots k-1]</tex>, <tex>b_2=s[j \ldots j+k-1]</tex>, <tex>b_3=s[0 \ldots z-1]</tex>. Тогда заметим, что <tex>b_3 = s[i \ldots i+z-1]</tex> и тогда возможны три случая: | ||
| + | |||
| + | # <tex>k<k_1</tex>. | ||
| + | #: Тогда <tex>b_1 \subset s[0 \ldots k_1-1]=s[i+j \ldots i+j+k_1-1]</tex> и тогда очевидно, что мы не можем увеличить значение <tex>Z[i+j]</tex> и надо рассматривать уже <tex>i=i+j</tex>. | ||
| + | # <tex>k<z-j</tex> и <tex>k>k_1</tex>. | ||
| + | #: Тогда <tex>b_1 = b_2 \subset b_3 = s[i \ldots i+z-1] \Rightarrow b_1 = s[i+j \ldots i+j+k-1]</tex> и тогда очевидно, что <tex>Z[i+j]</tex> можно увеличить до <tex>k</tex>. | ||
| + | # <tex>k>z-j</tex> и <tex>k>k_1</tex>. | ||
| + | #: Тогда <tex>b_1 = b_2 </tex>, но <tex>b_2</tex> не является подстрокой строки <tex>b_3</tex> (так как<tex>j+k-1 > z</tex>). Так как известно, что <tex>s[z] \ne s[i+z]</tex>, то <tex>s[0 \ldots z-j] = s[i+j \ldots i+z-1]</tex> и тогда понятно, что <tex>Z[i+j]=z-j</tex>. | ||
| − | |||
<br> | <br> | ||
<br> | <br> | ||
| − | |||
<br> | <br> | ||
| − | + | <br> | |
| − | + | <br> | |
| − | + | <br> | |
| − | |||
===Псевдокод=== | ===Псевдокод=== | ||
| − | '''int[]''' buildZFunctionFromPrefixFunction('''int'''[] | + | '''int[]''' buildZFunctionFromPrefixFunction(P : '''int'''[n]) |
| − | + | '''int'''[] Z = '''int'''[n] | |
| − | '''int'''[] Z= | + | '''for''' i = 1 '''to''' n - 1 |
| − | '''for''' | + | '''if''' P[i] > 0 |
| − | '''if''' | ||
Z[i - P[i] + 1] = P[i] | Z[i - P[i] + 1] = P[i] | ||
| − | Z[0] = n | + | Z[0] = n |
| − | '''int''' | + | '''int''' i = 1 |
| − | ''' | + | '''while''' i < n |
| − | + | '''int''' t = i | |
| − | '''if''' | + | '''if''' Z[i] > 0 |
| − | '''for''' | + | '''for''' j = 1 '''to''' Z[i] - 1 |
| + | '''if''' Z[i + j] > Z[j] | ||
| + | '''break''' | ||
Z[i + j] = min(Z[j], Z[i] - j) | Z[i + j] = min(Z[j], Z[i] - j) | ||
t = i + j | t = i + j | ||
| − | i = t | + | i = t + 1 |
'''return''' Z | '''return''' Z | ||
| + | |||
| + | ===Время работы=== | ||
| + | Внешний цикл <tex>\mathrm{while}</tex> отработает за <tex>O(n)</tex> итераций, так как внутри него <tex>i</tex> увеличивается не менее чем на <tex>1</tex>. А внутренний цикл выполнит суммарно не более <tex>O(n)</tex> итераций, так как после него <tex>i</tex> увеличится на количество итераций внутреннего цикла, но <tex>i</tex> не может увеличиться более чем на <tex>n</tex>, так как каждое значение <tex>Z[i]</tex> не может превзойти <tex>n</tex>. | ||
== См. также == | == См. также == | ||
| Строка 159: | Строка 189: | ||
* [http://habrahabr.ru/post/113266/ Поиск подстроки и смежные вопросы — Хабр]<br> | * [http://habrahabr.ru/post/113266/ Поиск подстроки и смежные вопросы — Хабр]<br> | ||
* [[wikipedia:ru:Z-функция | Википедия — Z-функция]]<br> | * [[wikipedia:ru:Z-функция | Википедия — Z-функция]]<br> | ||
| − | * [http://codeforces.ru/blog/entry/9612/ Переход между Z- и префикс- функциями] | + | * [http://codeforces.ru/blog/entry/9612/ Codeforces — Переход между Z- и префикс- функциями] |
[[Категория: Дискретная математика и алгоритмы]] | [[Категория: Дискретная математика и алгоритмы]] | ||
[[Категория: Поиск подстроки в строке]] | [[Категория: Поиск подстроки в строке]] | ||
[[Категория:Точный поиск]] | [[Категория:Точный поиск]] | ||
Текущая версия на 19:12, 4 сентября 2022
| Определение: |
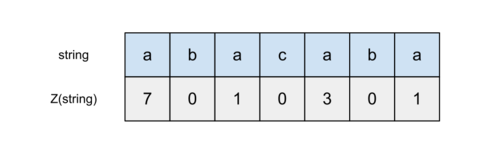
| Z-функция (англ. Z-function) от строки и позиции — это длина максимального префикса подстроки, начинающейся с позиции в строке , который одновременно является и префиксом всей строки . Более формально, . Значение Z-функции от первой позиции не определено, поэтому его обычно приравнивают к нулю или к длине строки. |
Примечание: далее в конспекте символы строки нумеруются с нуля.
Содержание
Тривиальный алгоритм
Простая реализация за , где — длина строки. Для каждой позиции перебираем для неё ответ, начиная с нуля, пока не обнаружим несовпадение или не дойдем до конца строки.
Псевдокод
int[] zFunction(s : string):
int[] zf = int[n]
for i = 1 to n − 1
while i + zf[i] < n and s[zf[i]] == s[i + zf[i]]
zf[i]++
return zf
Эффективный алгоритм поиска
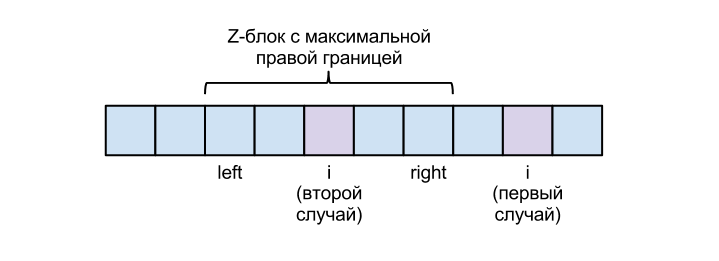
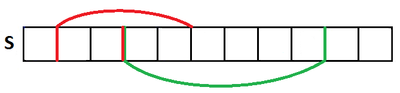
Z-блоком назовем подстроку с началом в позиции и длиной .
Для работы алгоритма заведём две переменные: и — начало и конец Z-блока строки с максимальной позицией конца (среди всех таких Z-блоков, если их несколько, выбирается наибольший). Изначально и .
Пусть нам известны значения Z-функции от до . Найдём .
Рассмотрим два случая.
- :
Просто пробегаемся по строке и сравниваем символы на позициях и .Пусть первая позиция в строке для которой не выполняется равенство , тогда это и Z-функция для позиции . Тогда . В данном случае будет определено корректное значение в силу того, что оно определяется наивно, путем сравнения с начальными символами строки. - :
Сравним и . Если меньше, то надо просто наивно пробежаться по строке начиная с позиции и вычислить значение . Корректность в таком случае также гарантирована.Иначе мы уже знаем верное значение , так как оно равно значению .
Время работы
Этот алгоритм работает за , так как каждая позиция пробегается не более двух раз: при попадании в диапазон от до и при высчитывании Z-функции простым циклом.
Псевдокод
int[] zFunction(s : string):
int[] zf = int[n]
int left = 0, right = 0
for i = 1 to n − 1
zf[i] = max(0, min(right − i, zf[i − left]))
while i + zf[i] < n and s[zf[i]] == s[i + zf[i]]
zf[i]++
if i + zf[i] > right
left = i
right = i + zf[i]
return zf
Поиск подстроки в строке с помощью Z-функции
— длина текста. — длина образца.
Образуем строку s = pattern + # + text, где # — символ, не встречающийся ни в text, ни в pattern. Вычисляем Z-функцию от этой строки.
В полученном массиве, в позициях в которых значение Z-функции равно , по определению начинается подстрока, совпадающая с pattern.
Псевдокод
int substringSearch(text : string, pattern : string):
int[] zf = zFunction(pattern + '#' + text)
for i = m + 1 to n + 1
if zf[i] == m
return i
Построение строки по Z-функции
| Задача: |
| Необходимо восстановить строку по Z-функции, считая алфавит ограниченным. |
Описание алгоритма
Пусть в массиве хранятся значения Z-функции, в будет записан ответ. Пойдем по массиву слева направо.
Нужно узнать значение . Для этого посмотрим на значение : если , тогда в запишем ещё не использованный символ или последний использованный символ алфавита, если мы уже использовали все символы. Если , то нам нужно записать префикс длины строки . Но если при посимвольном записывании этого префикса в конец строки мы нашли такой (индекс последнего символа строки), что больше, чем длина оставшейся незаписанной части префикса, то мы перестаём писать этот префикс и пишем префикс длиной строки .
Для правильной работы алгоритма будем считать значение равным нулю.
Заметим, что не всегда удастся восстановить строку с ограниченным алфавитом неподходящего размера. Например, для строки массив Z-функций будет . Используя двоичный алфавит, мы получим строку , но её массив Z-функций отличается от исходного. Ошибка восстановления строки возникла, когда закончились новые символы алфавита.
Если строить строку по некорректному массиву значений Z-функции, то мы получим какую-то строку, но массив значений Z-функций от неё будет отличаться от исходного.
Время работы
Этот алгоритм работает за O(|S|), так как мы один раз проходим по массиву Z-функций.
Реализация
string buildFromZ(z : int[], alphabet : char[]):
string s = ""
int prefixLength = 0 // длина префикса, который мы записываем
int j // позиция символа в строке, который будем записывать
int newCharacter = 0 // индекс нового символа
for i = 0 to z.length - 1
// мы не пишем какой-то префикс и не будем писать новый
if z[i] = 0 and prefixLength = 0
if newCharacter < alphabet.length
s += alphabet[newCharacter]
newCharacter++
else
s += alphabet[newCharacter - 1]
// нам нужно запомнить, что мы пишем префикс
if z[i] > prefixLength
prefixLength = z[i]
j = 0
// пишем префикс
if prefixLength > 0
s += s[j]
j++
prefixLength--
return s
Доказательство корректности алгоритма
Докажем, что если нам дали корректную Z-функцию, то наш алгоритм построит строку с такой же Z-функцией.
Пусть — данная Z-функция, строку построил наш алгоритм, — массив значений Z-функции для . Покажем, что массивы и будут совпадать.
Рассмотрим похожий алгоритм, но с более худшей асимптотикой. Отличие будет в том, что при мы будем писать префикс полностью и возвращаться в позицию . Рассмотрим каждый шаг этого алгоритма. Если , то мы пишем символ, отличный от первого символа строки, поэтому , а значит . Если , то при записи мы будем получать , потому что мы переписали префикс строки. Но далее мы можем переписать этот префикс другим префиксом. Заметим, что новый префикс будет содержаться и в префиксе самой строки, поэтому пересечение двух префиксов будет состоять из одинаковых символов. Значит, префикс не будет изменяться, как и значение . Тогда массив совпадает с .
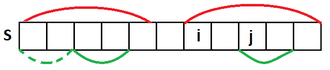
Покажем, что этот алгоритм эквивалентен нашему алгоритму. Когда мы пишем разные префиксы, то возможны три варианта: они не пересекаются (начало и конец одного префикса не принадлежат другому), один лежит внутри другого (начало и конец префикса принадлежит другому), они пересекаются (начало одного префикса пренадлежит другому, но конец не принадлежит).
- Если префиксы не пересекаются, то в алгоритме они не влияют друг на друга.
- Если префикс лежит внутри другого префикса, то записав большой префикс мы запишем и малый, поэтому не нужно возвращаться к началу малого префикса.
- Если префиксы пересекаются, то нам нужно переписать часть префикса, который начинается раньше, и начать писать другой префикс (начало этого префикса запишет конец префикса, начинающегося раньше). Если полностью переписать префикс, начинающийся раньше, то мы не сможем восстановить префикс, который начинался раньше конца первого префикса.
Таким образом, алгоритмы эквивалентны и наш алгоритм тоже корректен.
Построение Z-функции по префикс-функции
| Задача: |
| Дан массив с корректной префикс-функцией для строки . Требуется получить массив с Z-функцией для строки . |
Описание алгоритма
Пусть префикс функция хранится в массиве . Z-функцию будем записывать в массив . Заметим, что если , то мы можем заявить, что будет не меньше, чем .
Так же заметим, что после такого прохода в будет максимальное возможное значение. Далее будем поддерживать инвариант: в будет максимальное возможное значение.
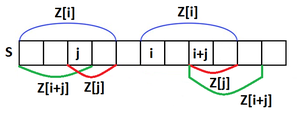
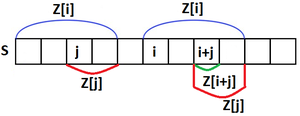
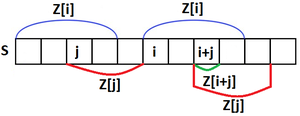
Пусть в , рассмотрю , и . Пусть , , . Тогда заметим, что и тогда возможны три случая:
- .
- Тогда и тогда очевидно, что мы не можем увеличить значение и надо рассматривать уже .
- и .
- Тогда и тогда очевидно, что можно увеличить до .
- и .
- Тогда , но не является подстрокой строки (так как). Так как известно, что , то и тогда понятно, что .
Псевдокод
int[] buildZFunctionFromPrefixFunction(P : int[n])
int[] Z = int[n]
for i = 1 to n - 1
if P[i] > 0
Z[i - P[i] + 1] = P[i]
Z[0] = n
int i = 1
while i < n
int t = i
if Z[i] > 0
for j = 1 to Z[i] - 1
if Z[i + j] > Z[j]
break
Z[i + j] = min(Z[j], Z[i] - j)
t = i + j
i = t + 1
return Z
Время работы
Внешний цикл отработает за итераций, так как внутри него увеличивается не менее чем на . А внутренний цикл выполнит суммарно не более итераций, так как после него увеличится на количество итераций внутреннего цикла, но не может увеличиться более чем на , так как каждое значение не может превзойти .