Rake-Compress деревья — различия между версиями
м (rollbackEdits.php mass rollback) |
|||
| (не показано 5 промежуточных версий 2 участников) | |||
| Строка 8: | Строка 8: | ||
==Идея== | ==Идея== | ||
===Описание=== | ===Описание=== | ||
| − | Пусть дано некоторое дерево <tex>T</tex>, для которого мы хотим выполнять описанные выше операции. Рассмотрим алгоритм ''сжатия дерева'' (англ. ''tree-contraction algorithm''), предложенный Миллером и Райфом. Алгоритм сжимает <tex>T</tex> в одну вершину путем применения операций <tex>\mathrm{Rake}</tex> и <tex>\mathrm{Compress}</tex> в несколько раундов: | + | Пусть дано некоторое дерево <tex>T</tex>, для которого мы хотим выполнять описанные выше операции. Рассмотрим алгоритм '''сжатия дерева''' (англ. ''tree-contraction algorithm''), предложенный Миллером и Райфом. Алгоритм сжимает <tex>T</tex> в одну вершину путем применения операций <tex>\mathrm{Rake}</tex> и <tex>\mathrm{Compress}</tex> в несколько раундов: |
* <tex>\mathrm{Rake}</tex> {{---}} все листья дерева сжимаются к своим родителям, | * <tex>\mathrm{Rake}</tex> {{---}} все листья дерева сжимаются к своим родителям, | ||
* <tex>\mathrm{Compress}</tex> {{---}} выбирается и объединяется некоторое множество несмежных друг с другом вершин, имеющих ровно одного сына. | * <tex>\mathrm{Compress}</tex> {{---}} выбирается и объединяется некоторое множество несмежных друг с другом вершин, имеющих ровно одного сына. | ||
| Строка 61: | Строка 61: | ||
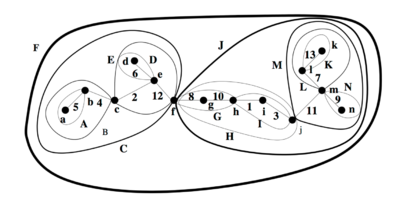
Например, для приведённого дерева на первом раунде сжатия применяется операция <tex>\mathrm{Rake}</tex> для вершин <tex>a</tex>, <tex>d</tex>, <tex>n</tex>, <tex>k</tex> и операция <tex>\mathrm{Compress}</tex> для <tex>g</tex> и <tex>i</tex>.<br><br> | Например, для приведённого дерева на первом раунде сжатия применяется операция <tex>\mathrm{Rake}</tex> для вершин <tex>a</tex>, <tex>d</tex>, <tex>n</tex>, <tex>k</tex> и операция <tex>\mathrm{Compress}</tex> для <tex>g</tex> и <tex>i</tex>.<br><br> | ||
| − | Сжатие может быть рассмотрено как рекурсивная кластеризация дерева в один '''кластер'''. Изначально вершины и рёбра составляют базовый кластер. Операции <tex>\mathrm{Rake}</tex> и <tex>\mathrm{Compress}</tex> формируют большие кластеры из нескольких меньших кластеров.<br><br>На иллюстрации примера все кластеры (кроме базового) обозначены зелёными лепестками. Каждый кластер помечен заглавной буквой метки вершины, входящей в него. Например, кластер <tex>A</tex>, полученный после сжатия вершины <tex>a</tex> содержит вершины <tex>a</tex>, <tex>b</tex> и ребро <tex>(a, b)</tex>; сжатая вершина <tex>g</tex> создает кластер <tex>G</tex>, содержащий эту вершину и рёбра <tex>(f, g)</tex> и <tex>(g, h)</tex>. Во втором раунде, после сжатия вершины <tex>b</tex> создается кластер <tex>B</tex>, содержащий кластер <tex>A</tex> и ребро <tex>(b, c)</tex>.<br>Представление сжатого дерева в виде кластеров: | + | Сжатие может быть рассмотрено как рекурсивная кластеризация дерева в один '''кластер''' (англ. ''cluster''). Изначально вершины и рёбра составляют базовый кластер. Операции <tex>\mathrm{Rake}</tex> и <tex>\mathrm{Compress}</tex> формируют большие кластеры из нескольких меньших кластеров.<br><br>На иллюстрации примера все кластеры (кроме базового) обозначены зелёными лепестками. Каждый кластер помечен заглавной буквой метки вершины, входящей в него. Например, кластер <tex>A</tex>, полученный после сжатия вершины <tex>a</tex> содержит вершины <tex>a</tex>, <tex>b</tex> и ребро <tex>(a, b)</tex>; сжатая вершина <tex>g</tex> создает кластер <tex>G</tex>, содержащий эту вершину и рёбра <tex>(f, g)</tex> и <tex>(g, h)</tex>. Во втором раунде, после сжатия вершины <tex>b</tex> создается кластер <tex>B</tex>, содержащий кластер <tex>A</tex> и ребро <tex>(b, c)</tex>.<br>Представление сжатого дерева в виде кластеров: |
[[Файл:RC_graph_clusters.png|400px|left|thumb|Кластеризованное дерево <tex>T</tex>.]] | [[Файл:RC_graph_clusters.png|400px|left|thumb|Кластеризованное дерево <tex>T</tex>.]] | ||
| Строка 85: | Строка 85: | ||
| − | Определим кластер как поддерево исходного дерева, порожденное множеством вершин. | + | |
| − | + | ||
| − | + | ||
| − | + | Определим кластер как поддерево исходного дерева, порожденное множеством вершин. | |
| − | + | ||
| − | + | Для кластера <tex>C</tex> скажем, что вершина <tex>v</tex> из <tex>C</tex> называется '''граничной вершиной''', если <tex>v</tex> смежная с вершинами не из <tex>C</tex>. '''Граница кластера''' {{---}} множество граничных вершин кластера, а '''степень кластера''' {{---}} количество граничных вершин кластера. | |
| − | |||
| − | |||
| − | |||
| − | |||
Например, для рассматриваемого дерева кластер <tex>A</tex> имеет границу <tex>\{b\}</tex> и степень <tex>1</tex>, а кластер <tex>G</tex> имеет границу <tex>\{f, g\}</tex> и степень <tex>2</tex>. При сжатии дерева все кластеры, кроме последнего, имеют степени <tex>1</tex> и <tex>2</tex>. Свойством алгоритмом сжатия является то, что: | Например, для рассматриваемого дерева кластер <tex>A</tex> имеет границу <tex>\{b\}</tex> и степень <tex>1</tex>, а кластер <tex>G</tex> имеет границу <tex>\{f, g\}</tex> и степень <tex>2</tex>. При сжатии дерева все кластеры, кроме последнего, имеют степени <tex>1</tex> и <tex>2</tex>. Свойством алгоритмом сжатия является то, что: | ||
Текущая версия на 19:37, 4 сентября 2022
Задача, которая решается с помощью динамических деревьев, формулируется следующим образом. Необходимо поддерживать лес деревьев и выполнять на нем следующие операции:
- — добавить ребро . Вершина должна быть корнем некоторого дерева. Вершины и должны находиться в разных деревьях,
- — удалить ребро . Ребро должно присутствовать в графе,
- — некоторый запрос относительно структуры дерева.
Содержание
Идея
Описание
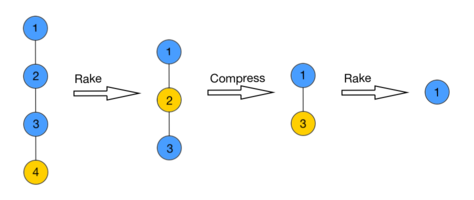
Пусть дано некоторое дерево , для которого мы хотим выполнять описанные выше операции. Рассмотрим алгоритм сжатия дерева (англ. tree-contraction algorithm), предложенный Миллером и Райфом. Алгоритм сжимает в одну вершину путем применения операций и в несколько раундов:
- — все листья дерева сжимаются к своим родителям,
- — выбирается и объединяется некоторое множество несмежных друг с другом вершин, имеющих ровно одного сына.
Сжатие дерева требует линейного времени и логарифмическое число раундов.
Для выбора вершин, которые будут удалены во время операции , применяется следующий метод: для каждой вершины генерируется рандомный бит и вершина добавляется в множество удаляемых только в том случае, когда она имеет одного ребёнка, бит для неё равен , а для родителя и ребёнка равен .
Рассмотрим, как изменяется количество вершин в дереве после применения к нему операций и .
Разобьём все вершины дерева на три группы:
- — входящая степень равна нулю,
- — входящая степень равна одному,
- — входящая степень больше одного.
| Лемма (1): |
. |
| Доказательство: |
|
Докажем по индукции по высоте дерева.
|
Заметим, что для леса деревьев лемма также справедлива.
| Лемма (2): |
После применения операций и к лесу, математическое ожидание количества вершин в нём не превосходит от их исходного числа. |
| Доказательство: |
|
Все листья будут удалены после операции , а каждая вершина, у которой ровно один сын, будет удалена с вероятностью после операции (так как мы рассматриваем три бита при выборе вершин и добавляем вершину в множество удаляемых только когда эти биты для родителя, вершины и ребёнка соответственно равны , и ). |
| Теорема: |
Математическое ожидание количества операций и , которые будут выполнены до полного сжатия дерева, равно , где — общее количество вершин. |
| Доказательство: |
| Из леммы 2 известно, что после каждой итерации применения операций и число вершин в среднем уменьшается в константное число раз. Значит, количество итераций в среднем ограничено . |
Для конкретного применения можно предположить, что рёбра дерева имеют вес, а вершины имеют метки.
Пример операций
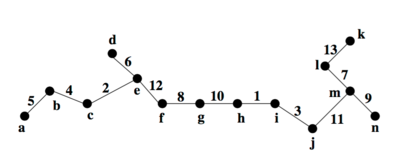
В качестве примера сжатия дерева рассмотрим следующее взвешенное дерево:
На каждом раунде сжатия (перечислены сверху вниз) удаляется множество вершин с использованием операций и :
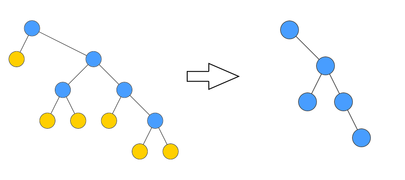
- Операция удаляет лист и ребро, смежное с ним, сохраняя в соседях данные: метку удалённой вершины, вес удалённого ребра и данные о сжатых на предыдущих раундах вершинах.
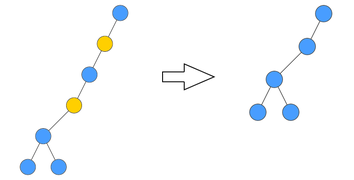
- Операция удаляет вершины, имеющие ровно одного сына, и смежные им рёбра. Например, для вершины c сыном и родителем будут удалены рёбра и . После этого добавляется ребро , а данные вершины и удалённых рёбер (метка удалённой вершины, сохранённые данные и веса удалённых рёбер) сохраняются в соседние вершины.
Например, для приведённого дерева на первом раунде сжатия применяется операция для вершин , , , и операция для и .
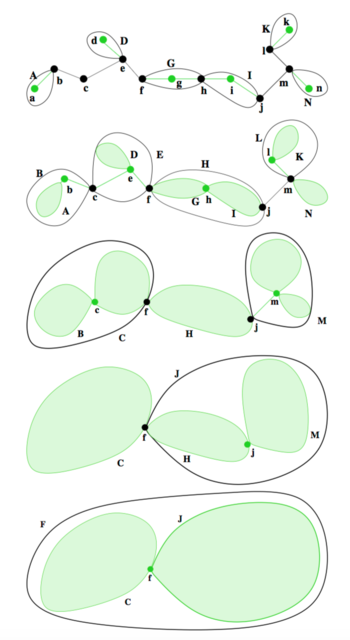
Сжатие может быть рассмотрено как рекурсивная кластеризация дерева в один кластер (англ. cluster). Изначально вершины и рёбра составляют базовый кластер. Операции и формируют большие кластеры из нескольких меньших кластеров.
На иллюстрации примера все кластеры (кроме базового) обозначены зелёными лепестками. Каждый кластер помечен заглавной буквой метки вершины, входящей в него. Например, кластер , полученный после сжатия вершины содержит вершины , и ребро ; сжатая вершина создает кластер , содержащий эту вершину и рёбра и . Во втором раунде, после сжатия вершины создается кластер , содержащий кластер и ребро .
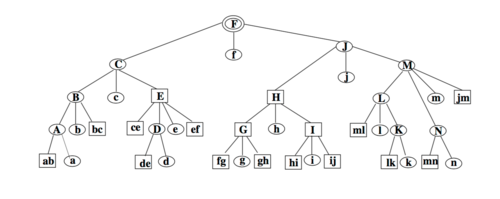
Представление сжатого дерева в виде кластеров:
Определим кластер как поддерево исходного дерева, порожденное множеством вершин.
Для кластера скажем, что вершина из называется граничной вершиной, если смежная с вершинами не из . Граница кластера — множество граничных вершин кластера, а степень кластера — количество граничных вершин кластера.
Например, для рассматриваемого дерева кластер имеет границу и степень , а кластер имеет границу и степень . При сжатии дерева все кластеры, кроме последнего, имеют степени и . Свойством алгоритмом сжатия является то, что:
- операции создают кластеры со степенью ,
- операции создают кластеры со степенью ,
- финальный кластер имеет степень .
Процесс сжатия исходного дерева может быть представлен в виде нового дерева, называемого .
Пример такого дерева для рассматриваемого исходного дерева:
Поскольку матожидание количества раундов — логарифм, то такое дерево будет сбалансированным.
дерево можно использовать для ответа на динамические запросы для статического дерева. Для этого в дереве сохраним требуемую информацию (необходимо модифицировать для пересчёта информации операции и ) и используем обход для ответа на запросы. Поскольку дерево с большой вероятностью является сбалансированным, обход дерева также можно осуществить за логарифм.
Для динамических деревьев, например, если доступны операции добавления/удаления ребра (операции и ), нужно эффективно перестраивать отдельные кластеры, пересчитывая данные. Для этого можно обновлять данные начиная с листа дерева, соответствующего обновляемой вершине в исходном дереве, и подниматься вверх.
Реализация
Хранение
Для того, чтобы отвечать на запросы относительно структуры леса необходимо сохранить информацию о том, как происходил процесс сжатия леса. Для этого будем хранить таблицу, в каждой строке которой записана информация о структуре леса после выполнения операций. Каждая клетка таблицы будет хранить информацию о вершине после выполнения операций и . Из информации будем сохранять родителя вершины, множество детей и метку, сжата ли вершина.
Пример таблицы для следующей последовательности операций:
| Шаг | Операция | ||||
|---|---|---|---|---|---|
| 4 | Родитель: — Дети: |
— | — | — | |
| 3 | Родитель: — Дети: |
— | Родитель: Дети: |
— | |
| 2 | Родитель: — Дети: |
Родитель: Дети: |
Родитель: Дети: |
— | |
| 1 | Родитель: — Дети: |
Родитель: Дети: |
Родитель: Дети: |
Родитель: Дети: |
Для того, чтобы выбирать множество вершин для применения операции будем использовать следующий метод: для каждой вершины с помощью генератора псевдослучайных чисел выберем случайный бит. Вершина добавляется в множество, если у нее ровно один ребенок, она не является корнем и биты, которые были сгенерированы для нее, ребенка и родителя равны , и соответственно.
Рассмотрим более подробно, как необходимо хранить клетки таблицы дерева. Для вершины необходимо сохранить ее родителя, а также множество детей. Для того, чтобы обрабатывать каждую клетку таблицы за , нужно производить операции с множеством детей за .
Рассмотрим, в каких случаях можно сжать вершину:
- если детей у вершины больше одного, то ее точно нельзя сжать,
- если у неё нет детей, то ее можно сжать только во время операции
- если у вершины один ребёнок, то её возможно сжать во время операции .
Чтобы определить, можно ли применить операцию к вершине, в том случае, когда у нее один ребёнок, нужно узнать, какой бит был сгенерирован на текущей итерации для ребёнка (один из трёх битов, генерируемых при операции ). Для этого необходимо знать номер вершины-ребёнка. Значит, нам нужно определять, какие элементы находятся в множестве детей только в том случае, когда размер множества равен . Поэтому, всю информацию о множестве можно хранить с помощью двух величин — хранить количество элементов в множестве и сумму их номеров. Поддерживая сумму номеров детей и их количество, можно эффективно узнавать номер вершины-ребёнка, когда это необходимо. Данная оптимизация позволяет за получать номер ребёнка и за обновлять множество детей.
Если вершина является корнем, то в качестве ее родителя будем хранить ее номер. Кроме того необходимо хранить изменения, которые произойдут с клеткой при переходе к следующему слою: будем хранить, кто должен стать новым родителем, на сколько изменится количество детей, а также как изменится сумма их номеров. Все это необходимо для того, чтобы обрабатывать каждую изменившуюся клетку за .
Псевдокод хранения клетки таблицы:
- — номер вершины,
- — родитель вершины,
- — количество детей вершины,
- — сумма номеров детей,
- — новый родитель вершины после изменений,
- и — изменения, произведенные с полями и соответственно.
struct Cell:
int id, parent, cntChild, sumChild
int newParent, diffCntChild, diffSumChild
func applyChanges():
parent = newParent
sumChild += diffSumChild
cntChild += diffCntChild
diffCntChild = diffSumChild = 0
func addChild(v: int):
diffCntChild++
diffSumChild += v
func removeChild(v: int):
diffCntChild--
diffSumChild -= v
Для хранения дерева будем использовать следующие данные:
- — список клеток, которые ей соответствуют, для каждой вершины,
- — генератор псевдослучайных чисел,
- — счётчик количества примененных операций по изменению структуры леса,
- — массив, в котором для каждой вершины запишем номер последней операции, при обработки которой была изменена хотя бы одна клетка, которая соответствуют вершине: это позволит эффективно узнавать, была ли вершина уже помечена как поменявшаяся или нет.
struct RCTree(n: int):
RndGen rand = RandBitsGenerator()
int time = 0
for i = 0 to n
lastUpdateTime[i] = 0
cells[i] = []
Кроме запросов о структуре леса, деревья можно использовать для подсчета значений некоторых функций. Например, каждой вершине можно сопоставить некоторое значение и узнавать, чему равна сумма значений всех вершин, которые находятся в поддереве. Для этого в клетках таблицы дерева необходимо хранить не только состояние вершины, но и значение функции, посчитанной на части дерева, которое уже было сжато в вершину. Если функция является аддитивной, то ее пересчет аналогичен пересчету множества детей вершины. Так, если некоторая вершина сжимается к родителю, то в соответствующей родителю клетке необходимо обновить значение функции. При добавлении и удалении ребер необходимо в изменившихся клетках пересчитывать значение функции.
Построение
Рассмотрим, как работает алгоритм построения дерева. Будем строить таблицу по строкам. В каждый момент будем хранить множество вершин, которые еще не были сжаты, и перестраивать следующий слой. Также будем делать операции и одновременно. Чтобы определить, нужно ли сжимать вершину, воспользуемся следующим алгоритмом:
bool shouldRemoveVertex(c: Cell, rand, layer: int):
if c.cntChild == 0
return true
if c.cntChild > 1 or c.parent == c.id
return false
if getCellForVertex(c.sumChild).cntChild == 0
return false
if rand.getBit(c.id, layer) == 0 and rand.getBit(c.sumChild, layer) == 1 and rand.getBit(c.parent, layer) == 1:
return true
return false
Таким образом, алгоритм построения дерева выглядит следующим образом:
func build(parent: int[n]):
alive =
int layer = 0
for i = 0 to n // заполним таблицу вершинами изначального дерева
cells[i].add(Cell(parent[i]))
while
nextAlive =
for
Cell c = getCellForVertex(v) // получить клетку таблицы, соответствующую вершине
if shouldRemoveVertex(c, rand, layer)
if c.cntChild == 1
getCellForVertex(c.sumChild).newParent = c.parent
getCellForVertex(c.parent).addChild(c.sumChild)
if c.parent v
getCellForVertex(c.parent).remove(v)
else
nextAlive.add(v)
alive = nextAlive
for
Cell newCell = getCellForVertex(v).clone().applyChanges()
cells[v].add(newCell)
layer++
Операции удаления и добавления ребра
Как только некоторая вершина помечается как изменившаяся, отменим её действие на таблицу:
- Найдем момент времени, когда вершина сжимается к родителю.
- Рассмотрим, какие вершины поменяются при сжатии данной: это ее родитель (если он есть), а также сын (если он есть). Для каждой из этих вершин поменяем значения изменений, которые необходимо применить к состоянию.
- Пометим, что эти вершины поменялись на этом слое. Для этого на каждом слое будем хранить список вершин, которые на нем поменялись. А перед тем как обрабатывать очередной слой будем добавлять в множество изменившихся вершин вершины из соответствующего списка.
- Кроме удаления эффекта от изменившихся вершин также необходимо и добавить правильный эффект. Для этого будем для каждой из изменившихся вершин определять, как ее состояние меняется при переходе к следующему слою. Если вершина сжимается к ее родителю, то пометим родителя и ребенка (если он есть) и поменяем изменение, которое хранится в соответствующих клетках. А для пересчета состояния клеток воспользуемся значениями изменений, которые сохранены в клетках.
Рассмотрим, что происходит с таблицей при изменении одного ребра. Основная идея заключается в том, чтобы научится пересчитывать все изменения таблицы за время пропорциональное их количеству. Для этого будем эффективно поддерживать множество изменившихся клеток. В момент, когда вершина помечается, как изменившаяся, найдем, как она влияет на таблицу и отменим это влияние.
Для начала необходимо найти момент времени, когда вершина сжимается. В этот момент она влияет на не более чем две вершины. Изменим значения , и нужным образом. Также необходимо добавить эти вершины в множество изменившихся (в момент, когда будет обработан соответствующий слой). Поэтому, для каждого слоя еще будем хранить список вершин, которые должны быть помечены перед обработкой слоя.
Алгоритм обновления дерева:
func changeTree(: Edge): time = time + 1 affected = markAffected(u) // пусть из дерева было удалено ребро markAffected(v) cells[u].parent = u cells[v].cntChild-- cells[v].sumChild -= u int layer = 0 while for markAffected(v) for Cell c = getCellForVertex(v) if shouldRemoveVertex(v) cells[v].size = layer + 1 if c.cntChild == 1 getCellForVertex(c.sumChild).newParent = c.parent getCellForVertex(c.parent).addChild(c.sumChild) markAffected(c.sumChild) if c.parent v getCellForVertex(c.parent).removeChild(v) markAffected(c.parent) affected.remove(v) for Cell newCell = getCellForVertex(v).clone().applyChanges() cells[v][layer + 1] = newCell layer++ func markAffected(v: int): // пометить вершину как изменившуюся if lastUpdateTime[v] == time return // вершина уже помечена lastUpdateTime[v] = time affected.add(v) removeEffectOfVertex(v) func removeEffectOfVertex(v: int): // удалить отметку о том, что вершина была помечена изменившийся int layer = cells[v].size Cell c = cells[v][layer] if c.parent == v return cells[c].parent.removeChild(v) if c.cntChild == 1 cells[c.parent].addChild(c.sumChild) cells[c.sumChild].newParent = v
Сравнение с Link-Cut Tree
Для Link-Cut деревьев (основанных на splay-деревьях), как и для деревьев, время работы операций и — . В реальности деревья оказываются медленнее, чем деревья.
Отличительной особенностью деревьев является возможность параллельного построения: операции и можно выполнять параллельно для всех вершин. Если предположить, что множество детей можно пересчитывать за , то дерево можно построить за в модели PRAM[1] в случае наличия процессоров.
Кроме этого, деревья могут оказаться полезными, если необходимо пересчитывать значения не на путях, а на поддеревьях.
См. также
Примечания
Источники информации
- Wikipedia — Parallel Tree Contraction
- Б. Ю. Минаев — Реализация динамических Rake-Compress деревьев в случае отсутствия ограничения на степени вершин
- Acar, Blelloch, and Vittes — RC-Tree implementation
- R. Werneck — Design and Analysis of Data Structures for Dynamic Trees
- G. L. Miller, J. H. Reif — Parallel Tree Contraction, Journal of Advances in Computer Research Volume 5, 1989
- Umit A. Acar, Guy E. Blelloch, Jorge L. Vittes — An Experimental Analysis of Change Propagation in Dynamic Trees, 1-2005