Дерево палиндромов — различия между версиями
(→Описание структуры) |
м (rollbackEdits.php mass rollback) |
||
| (не показаны 52 промежуточные версии 7 участников) | |||
| Строка 1: | Строка 1: | ||
'''Дерево палиндромов''' (англ. ''palindromic tree'') {{---}} структура данных, позволяющая решить некоторые интересные задачи на палиндромы. | '''Дерево палиндромов''' (англ. ''palindromic tree'') {{---}} структура данных, позволяющая решить некоторые интересные задачи на палиндромы. | ||
| − | Эту структуру данных придумал Михаил Рубинчик<ref name="ref1">[http://codeforces.com/profile/MikhailRubinchik MikhailRubinchik | + | Эту структуру данных придумал Михаил Рубинчик<ref name="ref1">[http://codeforces.com/profile/MikhailRubinchik Codeforces {{---}} MikhailRubinchik]</ref> и рассказал её на летних сборах в Петрозаводске в 2014 году. Наиболее подробное о дереве палиндромов или овердреве (palindromic tree, eertree) можно прочитать в диссертации Михаил Рубинчика [http://www.pdmi.ras.ru/pdmi/dissertatiton/2016-05-25t000000-%D1%80%D1%83%D0%B1%D0%B8%D0%BD%D1%87%D0%B8%D0%BA-%D0%BC%D0%B8%D1%85%D0%B0%D0%B8%D0%BB-%D0%B2%D0%B0%D0%BB%D0%B5%D0%BD%D1%82%D0%B8%D0%BD%D0%BE%D0%B2%D0%B8%D1%87] |
== Описание структуры == | == Описание структуры == | ||
| − | Дерево палиндромов состоит из вершин | + | [[Дерево,_эквивалентные_определения|Дерево]] палиндромов состоит из вершин, каждая из которых соответствует палиндрому. Все вершины соответствуют разным палиндромам. Через <tex>u'</tex> будем обозначать строку, которой соответствует вершина <tex>u</tex>. |
| − | + | [[Основные_определения_теории_графов#def_graph_edge_1|Рёбра]] дерева палиндромов ориентированные и помечены символами. Ребро с символом <tex>x</tex> ведет из вершины <tex>u</tex> в вершину <tex>v</tex> тогда и только тогда, когда <tex>v'=xu'x</tex>. | |
[[Файл:palindrome_tree_nodes.png|Пример четырех вершин дерева палиндромов|border]] [[Файл:palindrome_tree_edge.png|В данном примере мы получаем палиндром aba добавлением символа a к обоим сторонам палиндрома b|border]] | [[Файл:palindrome_tree_nodes.png|Пример четырех вершин дерева палиндромов|border]] [[Файл:palindrome_tree_edge.png|В данном примере мы получаем палиндром aba добавлением символа a к обоим сторонам палиндрома b|border]] | ||
| − | |||
| − | |||
| + | Стоит обратить внимание на то, что название структуры данных выбрано не совсем удачно. На самом деле структура представляет из себя два дерева {{---}} одно для палиндромов чётной длины, другое для палиндромов нечётной длины. Обозначим корни этих деревьев за <tex>root_{even}</tex> и <tex>root_{odd}</tex> соответственно. | ||
| + | |||
| + | Помимо вершин и рёбер в дереве палиндромов также присутствуют ''суффиксные ссылки''. Для каждой вершины <tex>u</tex> её суффиксная ссылка ведет в такую вершину <tex>w</tex>, что <tex>w'</tex> является наибольшим суффиксом строки <tex>u'</tex> относительно других вершин. При этом важно понимать, что суффиксная ссылка из вершины одного дерева может вести как в то же, так и в другое дерево. | ||
| − | + | [[Файл:palindrome_tree_suffix_link.png|Мы добавили суффиксную ссылку (пунктирная линия) из aba к a потому, что a является наибольшим паллиндромом-суффиксом строки aba|border]] | |
| − | |||
| − | |||
| − | + | При реализации в целях экономии памяти мы не будем хранить для каждой вершины соответствующую ей строку-палиндром. Этот подход был бы неэффективным с точки зрения памяти. Вместо этого мы будем хранить только длину палиндрома (и для некоторых задач позицию палиндрома в строке). | |
| − | <tex>root_{even}</tex> будет соответствовать фиктивному палиндрому длины 0. | + | Итак, структура будет состоять из двух деревьев и, соответственно, двух корней. Для удобства реализации каждый корень будет соответствовать фиктивной строке. |
| + | * <tex>root_{odd}</tex> будет соответствовать палиндрому длины <tex>-1</tex>. Это нужно для того, чтобы не обрабатывать отдельно случай добавления палиндрома длины <tex>1</tex>. Теперь каждый раз при добавлении ребра из вершины <tex>u</tex> к вершине <tex>v</tex>, мы будем просто считать что <tex>|v'|=|u'| + 2</tex>. | ||
| + | * <tex>root_{even}</tex> будет соответствовать фиктивному палиндрому длины <tex>0</tex>. | ||
| − | + | Суффиксные ссылки обоих корней будут вести к вершине <tex>root_{odd}</tex>. Это соглашение нужно также для удобства реализации {{---}} теперь каждая вершина имеет суффиксную ссылку. | |
== Построение == | == Построение == | ||
| − | + | Опишем далее по шагам процесс построения дерева палиндромов для данной строки. Изначально оно состоит из двух фиктивных вершин, а далее будет достраиваться инкрементально после каждого рассмотренного символа строки. | |
| − | |||
| − | |||
| − | Будем также поддерживать максимальный палиндром-суффикс обработанного префикса <tex>p</tex>. Назовем его <tex>t</tex>. | + | {| style="background-color:#CCC;margin:0.5px" |
| + | |- | ||
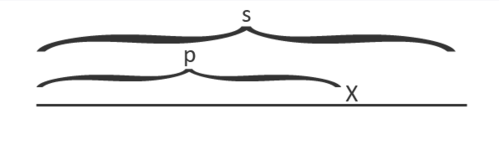
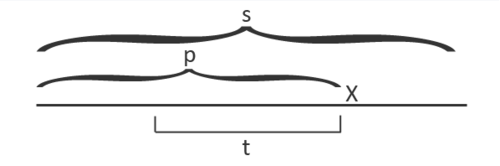
| + | |style="background-color:#FFF;padding:2px 30px"|Будем обрабатывать строку символ за символом. Пусть мы уже обработали некоторый префикс <tex>p</tex> и теперь хотим добавить следующий символ строки, назовем его <tex>x</tex>. | ||
| + | |style="background-color:#FFF;padding:2px 30px"|[[Файл:palindrome_tree_build1.png|500px]] | ||
| + | |- | ||
| + | |style="background-color:#FFF;padding:2px 30px"|Будем также поддерживать максимальный палиндром-суффикс обработанного префикса <tex>p</tex>. Назовем его <tex>t</tex>. | ||
| + | |style="background-color:#FFF;padding:2px 30px"|[[Файл:palindromic_tree_nodes.png|500px]] | ||
| + | |- | ||
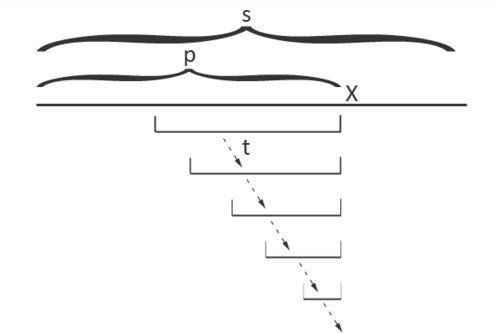
| + | |style="background-color:#FFF;padding:2px 30px"|Т.к. <tex>t</tex> находится в уже обработанной части строки, то ему соответствует какая-то вершина в дереве. У этой вершины есть суффиксная ссылка на какую-то другую вершину, у которой тоже есть суффиксная ссылка и т.д. | ||
| + | |style="background-color:#FFF;padding:2px 30px"|[[Файл:palindrome_tree_build3.png|500px|Цепочка суффиксных ссылок из t]] | ||
| + | |- | ||
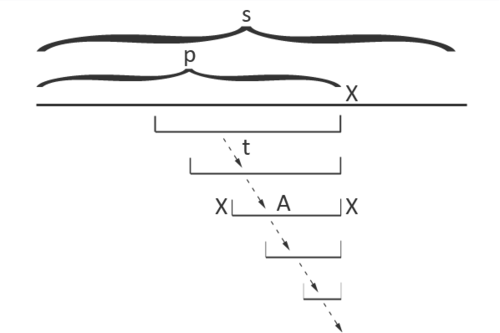
| + | |style="background-color:#FFF;padding:2px 30px"|Найдем теперь палиндром-суффикс строки <tex>px</tex> (т.е. нового префикса). Искомая строка будет иметь вид <tex>xAx</tex>, где <tex>A</tex> {{---}} какая-то строка, возможно пустая (или фиктивная строка длины <tex>-1</tex>, соответствующая корню <tex>root_{odd}</tex>, если искомый палиндром-суффикс {{---}} это просто символ <tex>x</tex>). | ||
| + | Т.к. <tex>xAx</tex> {{---}} палиндром, то <tex>A</tex> {{---}} тоже палиндром, и, более того, это суффикс строки <tex>p</tex>. Поэтому он может быть достигнут из <tex>t</tex> по суффиксным ссылкам. | ||
| + | |style="background-color:#FFF;padding:2px 30px"|[[Файл:palindrome_tree_build4.png|500px]] | ||
| + | |} | ||
| − | |||
| − | + | {{Утверждение | |
| + | |author=1 | ||
| + | |statement= | ||
| + | Строка <tex>xAx</tex> {{---}} это единственная подстрока-палиндром строки <tex>px</tex>, которой, возможно, нет в <tex>p</tex> (т.е. все другие подстроки-палиндромы есть). | ||
| + | |proof= | ||
| + | Заметим, что все новые подстроки-палиндромы, которых не было в <tex>p</tex>, должны оканчиваться на символ <tex>x</tex>, и поэтому должны быть палиндромом-суффиксом строки <tex>px</tex>. Из-за того, что <tex>xAx</tex> {{---}} наибольший палиндром-суффикс строки <tex>px</tex>, все остальные меньшие палиндромы-суффиксы этой строки уже есть в каком-то префиксе строки <tex>xAx</tex> (т.к. для каждого суффикса палиндрома есть равный ему префикс) и, соответственно, уже есть в <tex>p</tex>.}} | ||
| − | + | Таким образом, чтобы обработать очередной символ <tex>x</tex>, нужно просто спуститься по суффиксным ссылкам вершины <tex>t</tex> до тех пор, пока мы не найдем подходящую строку <tex>A</tex> (причем мы всегда можем найти такую строку, возможно длины <tex>-1</tex>, если очередная суффиксная ссылка будет вести в корень). Затем нужно проверить, есть ли уже ребро по символу <tex>x</tex> из вершины, соответствующей <tex>A</tex>, и если нет, добавить это ребро в новую вершину <tex>xAx</tex>. | |
| − | + | Теперь нужно добавить суффиксную ссылку из вершины <tex>xAx</tex>. Если эта вершина уже существовала до добавления символа <tex>x</tex>, ничего делать не нужно {{---}} суффиксная ссылка и так указывает на правильную вершину. Иначе нужно найти наибольший палиндром-суффикс строки <tex>xAx</tex>, который будет иметь вид <tex>xBx</tex>, где <tex>B</tex> {{---}} это некоторая строка, возможно, пустая. Следуя той же логике, которую мы использовали раньше, <tex>B</tex> {{---}} это палиндром-суффикс строки <tex>p</tex> и может быть достигнут из <tex>t</tex> по суффиксным ссылкам. | |
| − | |||
| − | |||
| − | + | {{Утверждение | |
| + | |author=2 | ||
| + | |statement= | ||
| + | Очередная добавленная вершина <tex>u</tex> не может быть максимальным палиндромом-суффиксом какой-либо ранее добавленной вершины <tex>v</tex> | ||
| + | |proof= | ||
| + | Предположим, что это не так. Тогда оказывается, что не все подпалиндромы строки <tex>v'</tex> были добавлены в дерево палиндромов ранее. А это противоречит утверждению 1. | ||
| + | }} | ||
| − | Таким образом, | + | Таким образом, добавление очередного символа по описанному алгоритму происходит корректно. |
| − | |||
| − | |||
== Оценка сложности == | == Оценка сложности == | ||
=== Память === | === Память === | ||
| − | Каждая вершина в дереве соответствует подпалиндрому, всего | + | Каждая вершина в дереве соответствует подпалиндрому, всего различных подпалиндромов в строке не более <tex>n</tex> (т.к. при добавлении очередного символа появляется не более одного нового палиндрома). |
Поэтому дерево палиндромов занимает <tex>O(n)</tex> памяти. | Поэтому дерево палиндромов занимает <tex>O(n)</tex> памяти. | ||
| Строка 58: | Строка 77: | ||
Таким образом, суммарное время работы построения алгоритма <tex>O(n)</tex>. | Таким образом, суммарное время работы построения алгоритма <tex>O(n)</tex>. | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
== Применения == | == Применения == | ||
| Строка 102: | Строка 82: | ||
{{Задача | {{Задача | ||
|definition= | |definition= | ||
| − | + | Необходимо определить число подпалиндромов, которые будут новыми после добавления символа <tex>x</tex> в конец строки <tex>s</tex>.}} | |
Например, при добавлении символа <tex>a</tex> к строке <tex>aba</tex>, которая уже состоит из палиндромов <tex>a</tex>, <tex>b</tex> и <tex>aba</tex>, добавляется новый палиндром <tex>aa</tex>. | Например, при добавлении символа <tex>a</tex> к строке <tex>aba</tex>, которая уже состоит из палиндромов <tex>a</tex>, <tex>b</tex> и <tex>aba</tex>, добавляется новый палиндром <tex>aa</tex>. | ||
Мы знаем, что число новых подпалиндромов при добавлении символа <tex>0</tex> или <tex>1</tex>. Так что решение задачи довольно простое {{---}} будем строить дерево палиндромов символ за символом и для каждого нового символа отвечать, был ли добавлен новый палиндром или нет (определить это можно, например, по тому, были ли добавлены новые вершины к структуре). | Мы знаем, что число новых подпалиндромов при добавлении символа <tex>0</tex> или <tex>1</tex>. Так что решение задачи довольно простое {{---}} будем строить дерево палиндромов символ за символом и для каждого нового символа отвечать, был ли добавлен новый палиндром или нет (определить это можно, например, по тому, были ли добавлены новые вершины к структуре). | ||
| + | |||
| + | |||
| + | Также данную структуру можно использовать для подсчета числа различных подпалиндромов строки. Это будет просто число вершин. | ||
=== Число подпалиндромов === | === Число подпалиндромов === | ||
{{Задача | {{Задача | ||
|definition= | |definition= | ||
| − | + | Требуется определить число подпалиндромов, которые содержатся в данной строке.}} | |
Например, строка <tex>aba</tex> имеет четыре подпалиндрома: дважды <tex>a</tex>, <tex>b</tex> и <tex>aba</tex>. | Например, строка <tex>aba</tex> имеет четыре подпалиндрома: дважды <tex>a</tex>, <tex>b</tex> и <tex>aba</tex>. | ||
| − | Для решения задачи | + | Для решения задачи будем строить дерево палиндромов для данной строки и на каждом шаге добавлять к ответу все палиндромы, которые содержат этот новый символ. |
| + | |||
| + | Рассмотрим очередной шаг алгоритма после добавления символа <tex>x</tex>. Обозначим за <tex>t</tex> вершину, соответствующую максимальному палиндрому-суффиксу, содержащую этот последний символ. | ||
| + | Заметим, что новые палиндромы, которые добавляет <tex>x</tex> {{---}} это <tex>t'</tex>, а также все палиндромы, достижимые из <tex>t</tex> по суффиксным ссылкам (т.к. только они содержат новый символ <tex>x</tex>). Для того чтобы быстро найти их число, будем хранить в каждой вершине длину цепочки суффиксных ссылок до корня (включая саму вершину), а затем будем просто прибавлять к ответу это число для каждого очередного <tex>t</tex> по мере добавления новых символов. | ||
| + | |||
Эта задача также может быть решена [[Алгоритм_Манакера|алгоритмом Манакера]] за ту же асимптотику, однако данный алгоритм не может быть расширен для более широкого класса задач, в отличие от дерева палиндромов. | Эта задача также может быть решена [[Алгоритм_Манакера|алгоритмом Манакера]] за ту же асимптотику, однако данный алгоритм не может быть расширен для более широкого класса задач, в отличие от дерева палиндромов. | ||
| Строка 122: | Строка 109: | ||
{{Задача | {{Задача | ||
|definition= | |definition= | ||
| − | Необходимо найти число вхождений каждого подпалиндрома строки в | + | Необходимо найти число вхождений каждого подпалиндрома строки в неё саму.}} |
Чтобы решить эту задачу деревом палиндромов, нужно обратить внимание на то, что при добавлении нового символа увеличивается количество вхождений наибольшего палиндрома-суффикса <tex>t</tex>, содержащего новый символ, и всех палиндромов, достижимых из <tex>t</tex> по суффиксным ссылкам. | Чтобы решить эту задачу деревом палиндромов, нужно обратить внимание на то, что при добавлении нового символа увеличивается количество вхождений наибольшего палиндрома-суффикса <tex>t</tex>, содержащего новый символ, и всех палиндромов, достижимых из <tex>t</tex> по суффиксным ссылкам. | ||
| − | Для каждой вершины <tex>u</tex> дерева палиндромов будем хранить число <tex>u | + | Для каждой вершины <tex>u</tex> дерева палиндромов будем хранить число вхождений строки <tex>u'</tex> в исходную строку (не обязательно актуальные данные) и число, которое необходимо добавить к числу вхождений всех потомков <tex>v</tex> вершины <tex>u</tex>. Назовем такую операцию добавления ''операцией релаксации''. После того, как релаксация будет выполнена для всех предков вершины <tex>u</tex>, можно будет считать, что посчитанное число вхождений соответствует действительности. |
| + | |||
Данный метод очень похож на метод, описанный в статье [[Несогласованные_поддеревья._Реализация_массового_обновления|про реализацию массовых обновлений в деревьях отрезков]]. | Данный метод очень похож на метод, описанный в статье [[Несогласованные_поддеревья._Реализация_массового_обновления|про реализацию массовых обновлений в деревьях отрезков]]. | ||
| Строка 136: | Строка 124: | ||
Для решения данной задачи применим тот же алгоритм, что и в прошлой задаче, а затем пройдем по всем вершинам дерева палиндромов и выберем подходящую. | Для решения данной задачи применим тот же алгоритм, что и в прошлой задаче, а затем пройдем по всем вершинам дерева палиндромов и выберем подходящую. | ||
| − | ==Примечания== | + | == См. также == |
| + | * [[Алгоритм Манакера]] | ||
| + | * [[Сжатое суффиксное дерево]] | ||
| + | * [[Суффиксный массив]] | ||
| + | |||
| + | == Примечания == | ||
<references/> | <references/> | ||
== Источники информации == | == Источники информации == | ||
| − | * [http://adilet.org/blog/25-09-14/ | + | * [http://adilet.org/blog/25-09-14/ Adilet.org {{---}} Palindromic tree, Adilet ADJA Zhaxybay] |
[[Категория:Алгоритмы и структуры данных]] | [[Категория:Алгоритмы и структуры данных]] | ||
Текущая версия на 19:03, 4 сентября 2022
Дерево палиндромов (англ. palindromic tree) — структура данных, позволяющая решить некоторые интересные задачи на палиндромы.
Эту структуру данных придумал Михаил Рубинчик[1] и рассказал её на летних сборах в Петрозаводске в 2014 году. Наиболее подробное о дереве палиндромов или овердреве (palindromic tree, eertree) можно прочитать в диссертации Михаил Рубинчика [1]
Описание структуры
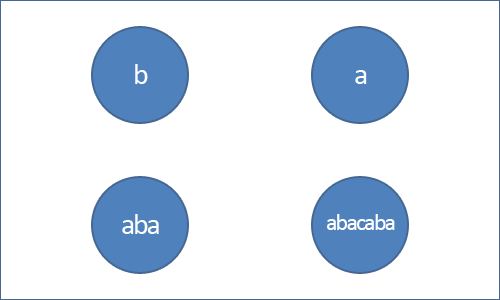
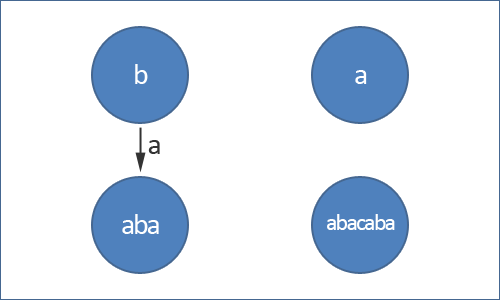
Дерево палиндромов состоит из вершин, каждая из которых соответствует палиндрому. Все вершины соответствуют разным палиндромам. Через будем обозначать строку, которой соответствует вершина . Рёбра дерева палиндромов ориентированные и помечены символами. Ребро с символом ведет из вершины в вершину тогда и только тогда, когда .
Стоит обратить внимание на то, что название структуры данных выбрано не совсем удачно. На самом деле структура представляет из себя два дерева — одно для палиндромов чётной длины, другое для палиндромов нечётной длины. Обозначим корни этих деревьев за и соответственно.
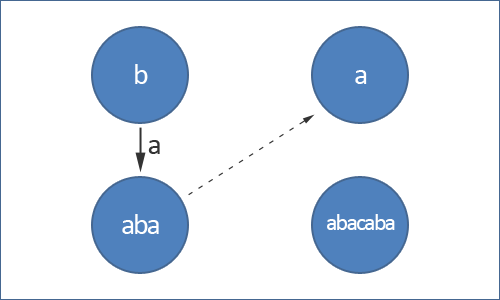
Помимо вершин и рёбер в дереве палиндромов также присутствуют суффиксные ссылки. Для каждой вершины её суффиксная ссылка ведет в такую вершину , что является наибольшим суффиксом строки относительно других вершин. При этом важно понимать, что суффиксная ссылка из вершины одного дерева может вести как в то же, так и в другое дерево.
При реализации в целях экономии памяти мы не будем хранить для каждой вершины соответствующую ей строку-палиндром. Этот подход был бы неэффективным с точки зрения памяти. Вместо этого мы будем хранить только длину палиндрома (и для некоторых задач позицию палиндрома в строке).
Итак, структура будет состоять из двух деревьев и, соответственно, двух корней. Для удобства реализации каждый корень будет соответствовать фиктивной строке.
- будет соответствовать палиндрому длины . Это нужно для того, чтобы не обрабатывать отдельно случай добавления палиндрома длины . Теперь каждый раз при добавлении ребра из вершины к вершине , мы будем просто считать что .
- будет соответствовать фиктивному палиндрому длины .
Суффиксные ссылки обоих корней будут вести к вершине . Это соглашение нужно также для удобства реализации — теперь каждая вершина имеет суффиксную ссылку.
Построение
Опишем далее по шагам процесс построения дерева палиндромов для данной строки. Изначально оно состоит из двух фиктивных вершин, а далее будет достраиваться инкрементально после каждого рассмотренного символа строки.
| Утверждение (1): |
Строка — это единственная подстрока-палиндром строки , которой, возможно, нет в (т.е. все другие подстроки-палиндромы есть). |
| Заметим, что все новые подстроки-палиндромы, которых не было в , должны оканчиваться на символ , и поэтому должны быть палиндромом-суффиксом строки . Из-за того, что — наибольший палиндром-суффикс строки , все остальные меньшие палиндромы-суффиксы этой строки уже есть в каком-то префиксе строки (т.к. для каждого суффикса палиндрома есть равный ему префикс) и, соответственно, уже есть в . |
Таким образом, чтобы обработать очередной символ , нужно просто спуститься по суффиксным ссылкам вершины до тех пор, пока мы не найдем подходящую строку (причем мы всегда можем найти такую строку, возможно длины , если очередная суффиксная ссылка будет вести в корень). Затем нужно проверить, есть ли уже ребро по символу из вершины, соответствующей , и если нет, добавить это ребро в новую вершину .
Теперь нужно добавить суффиксную ссылку из вершины . Если эта вершина уже существовала до добавления символа , ничего делать не нужно — суффиксная ссылка и так указывает на правильную вершину. Иначе нужно найти наибольший палиндром-суффикс строки , который будет иметь вид , где — это некоторая строка, возможно, пустая. Следуя той же логике, которую мы использовали раньше, — это палиндром-суффикс строки и может быть достигнут из по суффиксным ссылкам.
| Утверждение (2): |
Очередная добавленная вершина не может быть максимальным палиндромом-суффиксом какой-либо ранее добавленной вершины |
| Предположим, что это не так. Тогда оказывается, что не все подпалиндромы строки были добавлены в дерево палиндромов ранее. А это противоречит утверждению 1. |
Таким образом, добавление очередного символа по описанному алгоритму происходит корректно.
Оценка сложности
Память
Каждая вершина в дереве соответствует подпалиндрому, всего различных подпалиндромов в строке не более (т.к. при добавлении очередного символа появляется не более одного нового палиндрома). Поэтому дерево палиндромов занимает памяти.
Время
Чтобы оценить временную сложность алгоритма, нужно заметить, что по мере того, как мы обрабатываем строку символ за символом, левая граница наибольшего палиндрома-суффикса уже обработанной строки сдвигается только вправо. Очевидно, эта граница может двигаться вправо не более , где — длина строки, для которой мы строим дерево. То же самое относится и к левой границе той строки, на которую ведет суффиксная ссылка вновь добавленной вершины.
Таким образом, суммарное время работы построения алгоритма .
Применения
Число новых палиндромов, порождаемых очередным символом
| Задача: |
| Необходимо определить число подпалиндромов, которые будут новыми после добавления символа в конец строки . |
Например, при добавлении символа к строке , которая уже состоит из палиндромов , и , добавляется новый палиндром .
Мы знаем, что число новых подпалиндромов при добавлении символа или . Так что решение задачи довольно простое — будем строить дерево палиндромов символ за символом и для каждого нового символа отвечать, был ли добавлен новый палиндром или нет (определить это можно, например, по тому, были ли добавлены новые вершины к структуре).
Также данную структуру можно использовать для подсчета числа различных подпалиндромов строки. Это будет просто число вершин.
Число подпалиндромов
| Задача: |
| Требуется определить число подпалиндромов, которые содержатся в данной строке. |
Например, строка имеет четыре подпалиндрома: дважды , и .
Для решения задачи будем строить дерево палиндромов для данной строки и на каждом шаге добавлять к ответу все палиндромы, которые содержат этот новый символ.
Рассмотрим очередной шаг алгоритма после добавления символа . Обозначим за вершину, соответствующую максимальному палиндрому-суффиксу, содержащую этот последний символ. Заметим, что новые палиндромы, которые добавляет — это , а также все палиндромы, достижимые из по суффиксным ссылкам (т.к. только они содержат новый символ ). Для того чтобы быстро найти их число, будем хранить в каждой вершине длину цепочки суффиксных ссылок до корня (включая саму вершину), а затем будем просто прибавлять к ответу это число для каждого очередного по мере добавления новых символов.
Эта задача также может быть решена алгоритмом Манакера за ту же асимптотику, однако данный алгоритм не может быть расширен для более широкого класса задач, в отличие от дерева палиндромов.
Число вхождений каждого подпалиндрома в строку
| Задача: |
| Необходимо найти число вхождений каждого подпалиндрома строки в неё саму. |
Чтобы решить эту задачу деревом палиндромов, нужно обратить внимание на то, что при добавлении нового символа увеличивается количество вхождений наибольшего палиндрома-суффикса , содержащего новый символ, и всех палиндромов, достижимых из по суффиксным ссылкам.
Для каждой вершины дерева палиндромов будем хранить число вхождений строки в исходную строку (не обязательно актуальные данные) и число, которое необходимо добавить к числу вхождений всех потомков вершины . Назовем такую операцию добавления операцией релаксации. После того, как релаксация будет выполнена для всех предков вершины , можно будет считать, что посчитанное число вхождений соответствует действительности.
Данный метод очень похож на метод, описанный в статье про реализацию массовых обновлений в деревьях отрезков.
Поиск рефрен-палиндрома
| Задача: |
| Для данной строки необходимо найти палиндром, произведение длины которого на количество вхождений в строку является максимальным. |
Для решения данной задачи применим тот же алгоритм, что и в прошлой задаче, а затем пройдем по всем вершинам дерева палиндромов и выберем подходящую.