Группы графов — различия между версиями
Ashkroft (обсуждение | вклад) |
м (rollbackEdits.php mass rollback) |
||
| (не показано 27 промежуточных версий 2 участников) | |||
| Строка 1: | Строка 1: | ||
| + | ==Вершинная и рёберная группы графов== | ||
{{Определение | {{Определение | ||
|definition= | |definition= | ||
| − | + | '''Автоморфизмом''' (англ. ''Automorphism'') графа <tex>G</tex> называется изоморфизм графа <tex>G</tex> на себя | |
| − | |||
| − | |||
| − | |||
| − | |||
}} | }} | ||
| + | |||
| + | Каждый автоморфизм <tex>\alpha</tex> графа <tex>G</tex> есть [[:группа#Группа_подстановок|подстановка]] множества вершин <tex>V</tex>, сохраняющая смежность. Конечно, подстановка <tex>\alpha</tex> переводит любую вершину графа в вершину той же степени. Очевидно, что последовательное выполнение двух автоморфизмов есть также автоморфизм; | ||
{{Определение | {{Определение | ||
|definition= | |definition= | ||
| − | ''' | + | Автоморфизмы графа <tex> G </tex> образуют [[:группа#Группа_подстановок|группу подстановок]] <tex> \Gamma (G) </tex>, действующую на множестве вершин <tex>V(G)</tex>. Эту [[:группа|группу]] называют '''группой''' или иногда '''вершинной группой графа''' <tex>G</tex> (англ. ''point-group''). |
}} | }} | ||
{{Определение | {{Определение | ||
|definition= | |definition= | ||
| − | + | Вершинная группа графа <tex>G</tex> индуцирует другую группу подстановок <tex> \Gamma_1 (G) </tex>, называемую '''реберной группой графа''' <tex>G</tex> (англ. ''line-group'') {{---}} она действует на множестве ребер <tex>E(G)</tex>. | |
}} | }} | ||
| − | {{ | + | [[Файл:fordm.png|right]] |
| − | | | + | |
| − | ''' | + | Для иллюстрации различия групп <tex>\Gamma</tex> и <tex>\Gamma_1</tex> рассмотрим граф <tex>K_4 - x</tex>, показанный на рисунке; его вершины помечены <tex>v_1 , v_2, v_3, v_4 </tex> а ребра <tex>x_1, x_2, x_3, x_4, x_5 </tex>. Вершинная группа <tex>\Gamma (K_4 - x) </tex> состоит из четырех подстановок |
| + | <tex>(v_1)(v_2)(v_3)(v_4); (v_1)(v_3)(v_2v_4); (v_2)(v_4)(v_1v_3); (v_1v_3)(v_2v_4).</tex> | ||
| + | |||
| + | Тождественная подстановка вершинной группы индуцирует тождественную подстановку на множестве ребер, в то время как подстановка <tex>(v_1)(v_3)(v_2v_4)</tex> индуцирует подстановку на множестве ребер, в которой ребро <tex>x_5</tex> остается на месте, <tex> x_1</tex> меняется с <tex>x_4</tex>, а <tex>x_2</tex> с <tex>x_3</tex>. Таким образом, реберная группа <tex>\Gamma_1 (K_4 - x) </tex> состоит из следующих подстановок, индуцируемых указанными выше элементами вершинной группы: | ||
| + | <tex>(x_1)(x_2)(x_3)(x_4)(x_5); (x_1x_4)(x_2x_3)(x_5); (x_1x_2)(x_3x_4)(x_5); (x_1x_3)(x_2x_4)(x_5).</tex> | ||
| + | |||
| + | Понятно, что реберная и вершинная группы графа <tex>K_4 - x</tex> изоморфны. Но они, конечно, не могут быть идентичными, так как степень группы <tex>\Gamma_1 (K_4 - x) </tex> равна <tex>5</tex>, а степень группы <tex>\Gamma (K_4 - x) </tex> равна <tex>4</tex>. | ||
| + | |||
| + | |||
| + | {{Теорема | ||
| + | |statement= | ||
| + | Реберная и вершинная группы графа <tex>G</tex> изоморфны тогда и только тогда, когда граф <tex>G</tex> имеет не более одной изолированной вершины, а граф <tex>K_2</tex> не является его компонентой. | ||
| + | |proof= | ||
| + | Пусть подстановка <tex>\alpha'</tex> группы <tex>\Gamma_1(G)</tex> индуцируется подстановкой <tex>\alpha</tex> группы <tex>\Gamma(G)</tex>. Из определения операции умножения в группе <tex>\Gamma_1(G)</tex> вытекает, что | ||
| + | <tex>\alpha'\beta'=\alpha\beta</tex> | ||
| + | |||
| + | для <tex>\forall \alpha,\beta \in \Gamma(G)</tex>. Поэтому отображение <tex>\alpha\rightarrow\alpha '</tex> является групповым гомоморфизмом группы <tex>\Gamma(G)</tex> на <tex>\Gamma_1(G)</tex>. Следовательно, <tex>\Gamma(G)\cong\Gamma_1(G)</tex> тогда и только тогда, когда ядро этого отображения тривиально. | ||
| + | |||
| + | <tex> \Rightarrow </tex> | ||
| + | |||
| + | :Для доказательства необходимости предположим, что <tex>\Gamma(G)\cong\Gamma_1(G)</tex>. Тогда из неравенства <tex>\alpha\not=i</tex>(<tex>i</tex> — тождественная подстановка) следует, что <tex>\alpha'\not=i</tex>. Если в графе <tex>G</tex> существуют две различные изолированные вершины <tex>v_1</tex> и <tex>v_2</tex>, то можно определить подстановку <tex>\alpha\in\Gamma(G)</tex>, положив <tex>\alpha(v_1) = v_2, \alpha(v_2) = v_1, \alpha(v) = v</tex> для <tex>\forall v \not= v_1,v_2 </tex>. Тогда <tex>\alpha\not=i</tex>, но <tex>\alpha'=i</tex>. Если <tex>K_2</tex> {{---}} компонента графа <tex>G</tex>, то, записав ребро графа <tex>K_2</tex> в виде <tex>x = v_1v_2</tex> и определив подстановку <tex>\alpha\in\Gamma(g)</tex> точно так же, как выше, получим <tex>\alpha\not=i</tex>, но <tex>\alpha'=i</tex>. | ||
| + | |||
| + | <tex> \Leftarrow </tex> | ||
| + | |||
| + | :Чтобы доказать достаточность, предположим, что граф <tex>G</tex> имеет не больше одной изолированной вершины и <tex>K_2</tex> не является его компонентой. Если группа <tex>\Gamma(G)</tex> тривиальна, то очевидно, что группа <tex>\Gamma_1(G)</tex> оставляет на месте каждое ребро и, следовательно, <tex>\Gamma_1(G)</tex> {{---}} тривиальная группа. Поэтому предположим, что существует подстановка <tex>\alpha\in\Gamma(G)</tex>, для которой <tex>\alpha(u)=v\not=u</tex>. Тогда степени вершин <tex>u</tex> и <tex>v</tex> равны. Поскольку вершины <tex>u</tex> и <tex>v</tex> не изолированы, их степени не равны нулю. Здесь возникает два случая. <tex<\par</tex> | ||
| + | |||
| + | :''Случай 1.'' Вершины <tex>u</tex> и <tex>v</tex> смежны. Пусть <tex>x=uv</tex>. Так как <tex>K_2</tex> не является компонентой графа <tex>G</tex>, то степени обеих вершин <tex>u</tex> и <tex>v</tex> больше единицы. Следовательно, существует такое ребро <tex>y \not= x</tex> инцидентное вершине <tex>u</tex>, что ребро <tex>\alpha'(y)</tex> инцидентно вершине <tex>v</tex>. Отсюда <tex>\alpha'(y) \not= y</tex>, и тогда <tex>\alpha'\not=i</tex>. | ||
| + | |||
| + | :''Случай 2.'' Вершины <tex>u</tex> и <tex>v</tex> не смежны. Пусть <tex>x</tex> — произвольное ребро, инцидентное вершине <tex>u</tex>. Тогда <tex>\alpha'(x) \not= x</tex>, следовательно, <tex>\alpha'\not=i</tex>. | ||
}} | }} | ||
| − | {{ | + | ==Операции на группах подстановок== |
| − | + | ||
| − | Каждый | + | Пусть <tex>A</tex> — группа подстановок порядка <tex>m = |A|</tex> и степени <tex>d</tex>, действующая на множестве <tex>X = \{x_1,x_2,\ldots,x_d\}</tex>, а <tex>B</tex> {{---}} другая группа подстановок порядка <tex>n = |B|</tex> и степени <tex>e</tex>, действующая на множестве <tex>Y = \{y_1,y_2,\ldots,y_e\}</tex>. Например, пусть <tex>A = C_3</tex> {{---}} циклическая группа порядка <tex>3</tex>, действующая на множестве <tex>X={1, 2, 3}</tex>. Эта группа состоит из трех подстановок <tex>(1)(2)(3), (123)</tex> и <tex>(132)</tex>. Если взять в качестве <tex>B</tex> симметрическую группу <tex>S_2</tex> порядка <tex>2</tex>, действующую на множестве <tex>Y = \{a,b\}</tex>, то получим две подстановки <tex>(a)(b)</tex> и <tex>(ab)</tex>. Проиллюстрируем на этих двух группах подстановок действие нескольких бинарных операций. |
| − | }} | + | |
| + | ===Сумма подстановок=== | ||
| + | <tex>A + B</tex> {{---}} это группа подстановок, действующая на объединении <tex>X \cup Y</tex> непересекающихся множеств <tex>X</tex> и <tex>Y</tex> элементы которой записываются в виде <tex>\alpha + \beta</tex> и представляют собой упорядоченные пары подстановок <tex>\alpha</tex> из <tex>A</tex> и <tex>\beta</tex> из <tex>B</tex>. Каждый элемент <tex>z</tex>, принадлежащий множеству <tex>X \cup Y</tex> преобразуется подстановкой <tex>\alpha + \beta</tex> по правилу | ||
| + | |||
| + | <tex> | ||
| + | (\alpha + \beta)(z) = | ||
| + | \begin{cases} | ||
| + | \alpha z, z \in X, \\ | ||
| + | \beta z, z \in Y. | ||
| + | \end{cases} | ||
| + | </tex> | ||
| + | |||
| + | |||
| + | Таким образом, группа <tex>C_3 + S_2</tex> содержит <tex>6</tex> подстановок, каждую из которых можно записать в виде суммы подстановок <tex>\alpha \in C_3</tex> и <tex>\beta\in S_2</tex>, как, например, <tex>(123)(ab)=(123)+(ab)</tex>. (степень равна <tex>5</tex>.) | ||
| + | |||
| + | ===Произведение групп=== | ||
| + | <tex>A \times B </tex> {{---}} это группа подстановок, действующая на множестве <tex>X\times Y</tex>, элементы которой записываются в виде <tex>\alpha\times\beta</tex> и представляют собой упорядоченные пары подстановок <tex>\alpha</tex> из <tex>A</tex> и <tex>\beta</tex> из <tex>B</tex>. Элемент <tex>(x,y)</tex> множества <tex>X\times Y</tex> преобразуется подстановкой <tex>\alpha\times\beta</tex> естественным образом: | ||
| + | |||
| + | |||
| + | <tex>(\alpha\times\beta)(x,y)=(\alpha x,\beta y)</tex> | ||
| + | |||
| + | |||
| + | Подстановкой в группе <tex>C_3\times S_2</tex>, которая соответствует подстановке <tex>(123)+(ab)</tex> будет <tex>(1a\ 2b\ 3a\ 1b\ 2a\ 3b)</tex>, где для краткости символ <tex>(1,a)</tex> заменен на <tex>1a</tex>. (Порядок и степень равны <tex>6</tex>.) | ||
| + | |||
| + | ===Композиция групп=== | ||
| + | <tex>A[B]</tex> группы <tex>A</tex> относительно группы <tex>B</tex> также действует на множестве <tex>X\times Y</tex>. Для любой подстановки <tex>\alpha</tex> из <tex>A</tex> и любой последовательности <tex>(\beta_1,\beta_2,\ldots,\beta_d)</tex>, содержащей <tex>d</tex> (не обязательно различных) подстановок из <tex>B</tex>, существует единственная подстановка из <tex>A[B]</tex>, которая записывается в виде <tex>(\alpha;\beta_1,\beta_2,\ldots,\beta_d)</tex>, такая, что для всякой пары <tex>(x_i , y_i)</tex> из <tex>X\times Y</tex> выполняется равенство | ||
| + | |||
| + | |||
| + | <tex>(\alpha;\beta_1,\beta_2,\ldots,\beta_d)(x_i , y_j) = (\alpha x_i,\beta_i y_j).</tex> | ||
| + | |||
| + | |||
| + | Композиция <tex>C_3 [S_2 ] </tex> имеет степень <tex>6</tex> и порядок <tex>24</tex>. Любую подстановку из <tex>C_3 [S_2 ] </tex> можно записать в таком виде, как она действует на множестве <tex>X\times Y</tex>. Вводя опять обозначение <tex>1a</tex> для упорядоченной пары <tex>(1,a)</tex> и используя формулу выше можно представить подстановку <tex>((123);(a)(b),(ab),(a)(b))</tex> в виде <tex>(1a\ 2a\ 3b\ 1b\ 2b\ 3a)</tex>. Заметим, что группа <tex>S_2 [C_3 ] </tex> имеет порядок <tex>18</tex> и поэтому не изоморфна группе <tex>C_3 [S_2 ] </tex>. | ||
| + | |||
| + | ===Степенная группа=== | ||
| + | (обозначается <tex>B^A</tex>) действует на множестве <tex>Y^X</tex> всех функций, отображающих <tex>X</tex> в <tex>Y</tex>. Будем всегда предполагать, что степенная группа действует на множестве, состоящем более чем из одной функции. Для каждой пары подстановок <tex>\alpha</tex> из <tex>A</tex> и <tex>\beta</tex> из <tex>B</tex> существует единственная подстановка из <tex>B^A</tex> (записывается <tex>\beta^\alpha</tex>), которая действует на любую функцию <tex>f</tex> из <tex>Y^X</tex> в соответствии со следующим соотношением, определяющим образ каждого элемента <tex>x\in X</tex> при отображении <tex>\beta^\alpha f</tex>: | ||
| + | |||
| + | |||
| + | <tex>(\beta^\alpha f)(x)=\beta f(\alpha x).</tex> | ||
| + | |||
| + | |||
| + | Степенная группа <tex>S_{2}^{C_3}</tex> имеет порядок <tex>6</tex> и степень <tex>8</tex>. Применяя формулу выше, видим, что подстановка этой группы, полученная из подстановок <tex>\alpha = (123)</tex> и <tex>\beta = (ab)</tex>, имеет один цикл длины <tex>2</tex> и один цикл длины <tex>6</tex>. | ||
| − | + | ==См. также== | |
| − | + | *[[Группа]] | |
| − | + | *[[wikipedia:ru:Автоморфизм_графа | Википедия {{---}} Автоморфизм_графа]] | |
| − | |||
| − | [[ | ||
==Источники информации== | ==Источники информации== | ||
* Харари Ф. Теория графов. М.: Мир, 1973. (Изд. 3, М.: КомКнига, 2006. — 296 с.) | * Харари Ф. Теория графов. М.: Мир, 1973. (Изд. 3, М.: КомКнига, 2006. — 296 с.) | ||
| + | |||
| + | [[Категория: Дискретная математика и алгоритмы]] | ||
| + | [[Категория: Основные определения теории графов]] | ||
| + | [[Категория: Теория групп]] | ||
Текущая версия на 19:17, 4 сентября 2022
Содержание
Вершинная и рёберная группы графов
| Определение: |
| Автоморфизмом (англ. Automorphism) графа называется изоморфизм графа на себя |
Каждый автоморфизм графа есть подстановка множества вершин , сохраняющая смежность. Конечно, подстановка переводит любую вершину графа в вершину той же степени. Очевидно, что последовательное выполнение двух автоморфизмов есть также автоморфизм;
| Определение: |
| Автоморфизмы графа образуют группу подстановок , действующую на множестве вершин . Эту группу называют группой или иногда вершинной группой графа (англ. point-group). |
| Определение: |
| Вершинная группа графа индуцирует другую группу подстановок , называемую реберной группой графа (англ. line-group) — она действует на множестве ребер . |
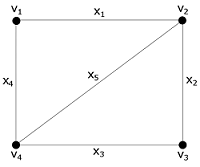
Для иллюстрации различия групп и рассмотрим граф , показанный на рисунке; его вершины помечены а ребра . Вершинная группа состоит из четырех подстановок
Тождественная подстановка вершинной группы индуцирует тождественную подстановку на множестве ребер, в то время как подстановка индуцирует подстановку на множестве ребер, в которой ребро остается на месте, меняется с , а с . Таким образом, реберная группа состоит из следующих подстановок, индуцируемых указанными выше элементами вершинной группы:
Понятно, что реберная и вершинная группы графа изоморфны. Но они, конечно, не могут быть идентичными, так как степень группы равна , а степень группы равна .
| Теорема: |
Реберная и вершинная группы графа изоморфны тогда и только тогда, когда граф имеет не более одной изолированной вершины, а граф не является его компонентой. |
| Доказательство: |
|
Пусть подстановка группы индуцируется подстановкой группы . Из определения операции умножения в группе вытекает, что для . Поэтому отображение является групповым гомоморфизмом группы на . Следовательно, тогда и только тогда, когда ядро этого отображения тривиально.
|
Операции на группах подстановок
Пусть — группа подстановок порядка и степени , действующая на множестве , а — другая группа подстановок порядка и степени , действующая на множестве . Например, пусть — циклическая группа порядка , действующая на множестве . Эта группа состоит из трех подстановок и . Если взять в качестве симметрическую группу порядка , действующую на множестве , то получим две подстановки и . Проиллюстрируем на этих двух группах подстановок действие нескольких бинарных операций.
Сумма подстановок
— это группа подстановок, действующая на объединении непересекающихся множеств и элементы которой записываются в виде и представляют собой упорядоченные пары подстановок из и из . Каждый элемент , принадлежащий множеству преобразуется подстановкой по правилу
Таким образом, группа содержит подстановок, каждую из которых можно записать в виде суммы подстановок и , как, например, . (степень равна .)
Произведение групп
— это группа подстановок, действующая на множестве , элементы которой записываются в виде и представляют собой упорядоченные пары подстановок из и из . Элемент множества преобразуется подстановкой естественным образом:
Подстановкой в группе , которая соответствует подстановке будет , где для краткости символ заменен на . (Порядок и степень равны .)
Композиция групп
группы относительно группы также действует на множестве . Для любой подстановки из и любой последовательности , содержащей (не обязательно различных) подстановок из , существует единственная подстановка из , которая записывается в виде , такая, что для всякой пары из выполняется равенство
Композиция имеет степень и порядок . Любую подстановку из можно записать в таком виде, как она действует на множестве . Вводя опять обозначение для упорядоченной пары и используя формулу выше можно представить подстановку в виде . Заметим, что группа имеет порядок и поэтому не изоморфна группе .
Степенная группа
(обозначается ) действует на множестве всех функций, отображающих в . Будем всегда предполагать, что степенная группа действует на множестве, состоящем более чем из одной функции. Для каждой пары подстановок из и из существует единственная подстановка из (записывается ), которая действует на любую функцию из в соответствии со следующим соотношением, определяющим образ каждого элемента при отображении :
Степенная группа имеет порядок и степень . Применяя формулу выше, видим, что подстановка этой группы, полученная из подстановок и , имеет один цикл длины и один цикл длины .
См. также
Источники информации
- Харари Ф. Теория графов. М.: Мир, 1973. (Изд. 3, М.: КомКнига, 2006. — 296 с.)