Блокирующий поток — различия между версиями
м (rollbackEdits.php mass rollback) |
|||
| (не показано 9 промежуточных версий 3 участников) | |||
| Строка 1: | Строка 1: | ||
{{Определение | {{Определение | ||
|definition= | |definition= | ||
| − | <b>Блокирующий поток</b> (англ. ''blocking flow'') {{---}} такой поток <tex>f</tex> в данной сети <tex>G</tex>, что любой <tex>s \leadsto t</tex> путь содержит насыщенное этим потоком ребро. Иными словами, в данной сети не найдётся такого пути из истока в сток, вдоль которого можно беспрепятственно увеличить поток. | + | <b>Блокирующий поток</b> (англ. ''blocking flow'') {{---}} такой [[Определение сети, потока|поток]] <tex>f</tex> в данной сети <tex>G</tex>, что любой <tex>s \leadsto t</tex> путь содержит насыщенное этим потоком ребро. Иными словами, в данной сети не найдётся такого пути из истока в сток, вдоль которого можно беспрепятственно увеличить поток. |
}} | }} | ||
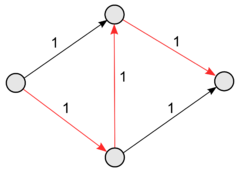
| − | + | Блокирующий поток не обязательно максимален (пример: см. рис. <tex>1</tex>). [[Теорема Форда-Фалкерсона]] говорит о том, что поток будет максимальным тогда и только тогда, когда в остаточной сети не найдётся <tex>s \leadsto t</tex> пути; в блокирующем же потоке ничего не утверждается о существовании пути по рёбрам, появляющимся в остаточной сети. | |
| − | |||
| − | Блокирующий поток не обязательно максимален (пример: см. рис. 1). [[Теорема Форда-Фалкерсона]] говорит о том, что поток будет максимальным тогда и только тогда, когда в остаточной сети не найдётся <tex>s \leadsto t</tex> пути; в блокирующем же потоке ничего не утверждается о существовании пути по рёбрам, появляющимся в остаточной сети. | ||
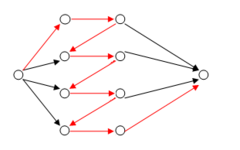
| − | Более того, величина блокирующего потока может быть сколь угодно мала по сравнению с величиной максимального потока в сети (пример: см. рис. 2). В примере поток является блокирующим и имеет величину 1, в то время как максимальный можно делать сколь угодно большим, увеличивая количество вершин по той же схеме. | + | Более того, величина блокирующего потока может быть сколь угодно мала по сравнению с величиной максимального потока в сети (пример: см. рис. <tex>2</tex>). В примере поток является блокирующим и имеет величину <tex>1</tex>, в то время как максимальный можно делать сколь угодно большим, увеличивая количество вершин по той же схеме. |
| + | |||
| + | Блокирующий поток используется в [[Схема алгоритма Диница|алгоритме Диница]]. Его поиск с помощью удаляющего обхода занимает <tex>O(VE)</tex> времени. | ||
| + | {|align="center" | ||
| + | |-valign="top" | ||
| + | |[[Файл:Блокпоток.png|240px|thumb|right|Рис. <tex>1</tex>. Пропускные способности всех рёбер равны единице, по красным рёбрам течёт единичный поток.]] | ||
| + | |[[Файл:Блокирующийпоток.png|240px|thumb|right|Рис. <tex>2</tex>. Пропускные способности всех рёбер равны единице, по красным рёбрам течёт единичный поток.]] | ||
| + | |} | ||
== См. также == | == См. также == | ||
| Строка 16: | Строка 21: | ||
== Источники == | == Источники == | ||
* [http://www.e-maxx.ru/algo/dinic Алгоритм Диница. Необходимые определения.] | * [http://www.e-maxx.ru/algo/dinic Алгоритм Диница. Необходимые определения.] | ||
| + | * [[wikipedia:Dinic's_algorithm | Wikipedia {{---}} Dinic's algorithm]] | ||
| + | * [[wikipedia:Алгоритм_Диница | Википедия {{---}} алгоритм Диница ]] | ||
[[Категория: Алгоритмы и структуры данных]] | [[Категория: Алгоритмы и структуры данных]] | ||
[[Категория: Задача о максимальном потоке ]] | [[Категория: Задача о максимальном потоке ]] | ||
Текущая версия на 19:17, 4 сентября 2022
| Определение: |
| Блокирующий поток (англ. blocking flow) — такой поток в данной сети , что любой путь содержит насыщенное этим потоком ребро. Иными словами, в данной сети не найдётся такого пути из истока в сток, вдоль которого можно беспрепятственно увеличить поток. |
Блокирующий поток не обязательно максимален (пример: см. рис. ). Теорема Форда-Фалкерсона говорит о том, что поток будет максимальным тогда и только тогда, когда в остаточной сети не найдётся пути; в блокирующем же потоке ничего не утверждается о существовании пути по рёбрам, появляющимся в остаточной сети.
Более того, величина блокирующего потока может быть сколь угодно мала по сравнению с величиной максимального потока в сети (пример: см. рис. ). В примере поток является блокирующим и имеет величину , в то время как максимальный можно делать сколь угодно большим, увеличивая количество вершин по той же схеме.
Блокирующий поток используется в алгоритме Диница. Его поиск с помощью удаляющего обхода занимает времени.