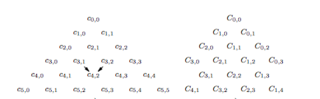Производящие функции нескольких переменных — различия между версиями
(sta) |
м (rollbackEdits.php mass rollback) |
||
| (не показано 29 промежуточных версий 6 участников) | |||
| Строка 1: | Строка 1: | ||
| − | + | {{Определение | |
| − | + | |definition= | |
| − | <tex>G(x, y) = \sum\limits_{n, k \geqslant 0} g_{n, k} x^n y^k</tex> | + | '''Производящие функции нескольких переменных''' (англ. ''multivariable generating function'') {{---}} обычные [[Производящая функция | производящие функции]], зависящие более, чем от одной переменной. Очень часто применяются функции от двух переменных (далее они и будут рассматриваться), которые в общем случае принимают вид: |
| − | + | ||
| + | <tex>G(x, y) = \sum\limits_{n, k \geqslant 0} g_{n, k} x^n y^k</tex>. | ||
| + | }} | ||
| − | + | Рассмотрим несколько примеров : | |
== Треугольник Паскаля == | == Треугольник Паскаля == | ||
| − | + | {{Определение | |
| − | + | |definition= | |
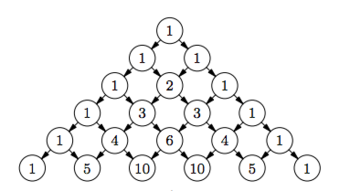
| − | Треугольник Паскаля ( | + | '''Треугольник Паскаля''' (англ. ''Pascal's triangle'') {{---}} бесконечная таблица биномиальных коэффициентов<ref>[https://ru.wikipedia.org/wiki/%D0%91%D0%B8%D0%BD%D0%BE%D0%BC%D0%B8%D0%B0%D0%BB%D1%8C%D0%BD%D1%8B%D0%B9_%D0%BA%D0%BE%D1%8D%D1%84%D1%84%D0%B8%D1%86%D0%B8%D0%B5%D0%BD%D1%82 Биномиальные коэффициенты]</ref>, имеющая треугольную форму. В этом треугольнике на вершине и по бокам стоят единицы. Каждое число равно сумме двух расположенных над ним чисел. |
| − | + | }} | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | [[File:Pascal_triangle.png|thumb|350px|right|Рис.<tex>1</tex>]] | |
| + | Элементы треугольника (рис.<tex>1</tex>) перечисляют пути, идущие из его вершины в соответствующую клетку. Пути имеют вид ломаных, составленных из векторов единичной длины двух видов: идущих вправо-вниз и идущих влево-вниз. | ||
Производящая функция может быть сопоставлена треугольнику Паскаля несколькими способами. Например, можно рассмотреть производящую функцию | Производящая функция может быть сопоставлена треугольнику Паскаля несколькими способами. Например, можно рассмотреть производящую функцию | ||
| − | <tex>\sum\limits_{n,k = 0}^{\infty} c_{n,k} x^k y^n = \sum\limits_{n,k = 0}^{\infty} \ | + | <tex>\displaystyle\sum\limits_{n,k = 0}^{\infty} c_{n,k} x^k y^n = \sum\limits_{n,k = 0}^{\infty} \binom{n}{k} x^k y^n = \sum\limits_{n = 0}^{\infty}</tex><tex>\Big(\sum\limits_{k = 0}^{n} \binom{n}{k} x^k\Big) y^n = \displaystyle\sum\limits_{n = 0}^{\infty} (1 + x)^n y^n = \dfrac{1}{1 - y - xy}</tex> |
| − | [[File:Pascal_triangle_3.png|thumb| | + | [[File:Pascal_triangle_3.png|thumb|320px|right|Рис.<tex>2</tex>]] |
| − | Второй способ | + | Второй способ соответствует нумерации элементов треугольника числом отрезков каждого типа на путях, ведущих в соответствующую точку (рис.<tex>2</tex>) <tex>C_{n,m} = c_{n+m, n} = \dbinom{n+m}{m}</tex>. Тогда производящая функция будет иметь вид |
| − | <tex>\sum\limits_{n,m = 0}^{\infty} C_{n, m} x^n y^m = \sum\limits_{n,m = 0}^{\infty} | + | <tex>\displaystyle\sum\limits_{n,m = 0}^{\infty} C_{n, m} x^n y^m = \sum\limits_{n,m = 0}^{\infty} \binom{n+m}{m} x^n y^m = \sum\limits_{k = 0}^{\infty}</tex><tex> \Big(\sum\limits_{n + m = k} \binom{n+m}{n} |
| − | x^n y^m = \sum\limits_{k = 0}^{\infty} (x + y)^k = \dfrac{1}{1 -x - y}</tex> | + | x^n y^m \Big)=\displaystyle\sum\limits_{k = 0}^{\infty} (x + y)^k = \dfrac{1}{1 -x - y}</tex> |
| − | Также существует еще один способ: сопоставить треугольнику Паскаля ''экспоненциальную производящую функцию''. Экспоненциальная производящая функция отличается от обычной тем, что в качестве коэффициентов степенного ряда берутся не элементы последовательности <tex>a_n</tex>, а числа <tex>\dfrac{a_n}{n!}</tex> | + | Также существует еще один способ: сопоставить треугольнику Паскаля ''экспоненциальную производящую функцию''. Экспоненциальная производящая функция отличается от обычной тем, что в качестве коэффициентов степенного ряда берутся не элементы последовательности <tex>a_n</tex>, а числа <tex>\dfrac{a_n}{n!}</tex>. |
==Экспоненциальные производящие функции== | ==Экспоненциальные производящие функции== | ||
| Строка 39: | Строка 38: | ||
<tex>\{ \alpha_n \} \mapsto \sum\limits_{n = 0}^{\infty} a_n \alpha_n s^n</tex> | <tex>\{ \alpha_n \} \mapsto \sum\limits_{n = 0}^{\infty} a_n \alpha_n s^n</tex> | ||
| − | определяемую последовательностью <tex>\{ \alpha_n \}</tex>. Если в последовательности <tex>\{ \alpha_n \}</tex> отсутствуют нулевые элементы, то такое сопоставление взаимно однозначно. До сих пор мы пользовались обычными производящими функциями | + | определяемую последовательностью <tex>\{ \alpha_n \}</tex>. Если в последовательности <tex>\{ \alpha_n \}</tex> отсутствуют нулевые элементы, то такое сопоставление взаимно однозначно. До сих пор мы пользовались обычными производящими функциями, отвечающими последовательности <tex>\{ \alpha_n \} \equiv 1</tex>. В зависимости от преследуемых целей могут принести и другие последовательности. |
{{Определение | {{Определение | ||
|definition= | |definition= | ||
| − | '''Производящие экспоненциальные функции'''(англ. ''exponential generating function'') - функции, | + | '''Производящие экспоненциальные функции''' (англ. ''exponential generating function'') {{---}} функции, соответствующие последовательности <tex>\{ \alpha_n \} = \dfrac{1}{n!}</tex>. |
}} | }} | ||
{{Определение | {{Определение | ||
|definition= | |definition= | ||
| − | Экспоненциальные производящие функции для целочисленных последовательностей называют '''функциями Гурвица'''(англ. ''Hurwitz function''). | + | Экспоненциальные производящие функции для целочисленных последовательностей называют '''функциями Гурвица''' (англ. ''Hurwitz function''). |
}} | }} | ||
Чем отличаются экспоненциальные производящие функции от обычных? Посмотрим на поведение экспоненциальных производящих функций при выполнении операции над ними. Сумма ведет себя обычным образом: | Чем отличаются экспоненциальные производящие функции от обычных? Посмотрим на поведение экспоненциальных производящих функций при выполнении операции над ними. Сумма ведет себя обычным образом: | ||
| − | <tex>\sum\limits_{n = 0}^{\infty} \dfrac{a_n}{n!}s^n + \sum\limits_{n = 0}^{\infty} \dfrac{ | + | <tex>\displaystyle\sum\limits_{n = 0}^{\infty} \dfrac{a_n}{n!}s^n + \sum\limits_{n = 0}^{\infty} \dfrac{b_n}{n!}s^n = \sum\limits_{n = 0}^{\infty} \dfrac{(a_n + b_n)}{n!} s^n</tex> |
| − | а с произведением по-другому : | + | а с произведением по-другому: |
<tex>\bigg(\dfrac{a_0}{0!} + \dfrac{a_1}{1!}s + \dfrac{a_2}{2!}s^2 + \ldots\bigg)\bigg(\dfrac{b_0}{0!} + \dfrac{b_1}{1!}s + \dfrac{b_2}{2!}s^2 + \ldots\bigg) = \dfrac{a_0}{0!} \dfrac{b_0}{0!} + \bigg(\dfrac{a_0}{0!} \dfrac{b_1}{1!} + \dfrac{a_1}{1!} \dfrac{b_0}{0!}\bigg)s + \bigg(\dfrac{a_0}{0!} \dfrac{b_2}{2!} + \dfrac{a_1}{1!} \dfrac{b_1}{1!} + \dfrac{a_2}{2!} \dfrac{b_0}{0!}\bigg)s^2 + \ldots</tex> | <tex>\bigg(\dfrac{a_0}{0!} + \dfrac{a_1}{1!}s + \dfrac{a_2}{2!}s^2 + \ldots\bigg)\bigg(\dfrac{b_0}{0!} + \dfrac{b_1}{1!}s + \dfrac{b_2}{2!}s^2 + \ldots\bigg) = \dfrac{a_0}{0!} \dfrac{b_0}{0!} + \bigg(\dfrac{a_0}{0!} \dfrac{b_1}{1!} + \dfrac{a_1}{1!} \dfrac{b_0}{0!}\bigg)s + \bigg(\dfrac{a_0}{0!} \dfrac{b_2}{2!} + \dfrac{a_1}{1!} \dfrac{b_1}{1!} + \dfrac{a_2}{2!} \dfrac{b_0}{0!}\bigg)s^2 + \ldots</tex> | ||
| Строка 61: | Строка 60: | ||
Коэффициенты <tex>\dfrac{c_n}{n!}</tex> произведения вычисляются по формуле | Коэффициенты <tex>\dfrac{c_n}{n!}</tex> произведения вычисляются по формуле | ||
| − | <tex>c_n = \begin{pmatrix} n \\ 0 \end{pmatrix} a_0 b_n + \begin{pmatrix} n \\ 1 \end{pmatrix} a_1 b_{n - 1} + \ldots + \begin{pmatrix} n \\ n \end{pmatrix} | + | <tex>c_n = \begin{pmatrix} n \\ 0 \end{pmatrix} a_0 b_n + \begin{pmatrix} n \\ 1 \end{pmatrix} a_1 b_{n - 1} + \ldots + \begin{pmatrix} n \\ n \end{pmatrix} a_n b_0</tex> |
| − | Еще одно существенное отличие экспоненциальных производящих функций от обычных наблюдается при взятии производных | + | Еще одно существенное отличие экспоненциальных производящих функций от обычных наблюдается при взятии производных и при интегрировании. Дифференцирование или интегрирование экспоненциальной производящей функции приводит к сдвигу последовательности ее коэффициентов без изменения их величины: |
<tex>\bigg( \dfrac{a_0}{0!} + \dfrac{a_1}{1!}s + \dfrac{a_2}{2!}s^2 + \ldots \bigg)^{'} = \dfrac{a_1}{0!} + \dfrac{a_2}{1!}s + \dfrac{a_3}{2!}s^2 + \ldots </tex> | <tex>\bigg( \dfrac{a_0}{0!} + \dfrac{a_1}{1!}s + \dfrac{a_2}{2!}s^2 + \ldots \bigg)^{'} = \dfrac{a_1}{0!} + \dfrac{a_2}{1!}s + \dfrac{a_3}{2!}s^2 + \ldots </tex> | ||
| − | <tex>\int \bigg(\dfrac{a_0}{0!} + \dfrac{a_1}{1!}s + \dfrac{a_2}{2!}s^2 + \ldots \bigg) = \dfrac{a_0}{1!}s + \dfrac{a_1}{2!}s^2 + \dfrac{a_2}{3!}s^3 + \dfrac{a_3}{4!}s^4 + \ldots </tex> | + | <tex>\displaystyle\int \bigg(\dfrac{a_0}{0!} + \dfrac{a_1}{1!}s + \dfrac{a_2}{2!}s^2 + \ldots \bigg) = \dfrac{a_0}{1!}s + \dfrac{a_1}{2!}s^2 + \dfrac{a_2}{3!}s^3 + \dfrac{a_3}{4!}s^4 + \ldots </tex> |
| − | Обычная производящая функция <tex>A(s) = a_0 + a_1s + a_2s^2 + \ldots</tex> выражается через экспоненциальную <tex> | + | Обычная производящая функция <tex>A(s) = a_0 + a_1s + a_2s^2 + \ldots</tex> выражается через экспоненциальную <tex>B(t) = \dfrac{a_0}{0!} + \dfrac{a_1}{1!}t + \dfrac{a_2}{2!}t^2 + \ldots </tex> по формуле |
| − | <tex>A(s) = \ | + | <tex>A(s) = \int\limits_{0}^{\infty} e^{-t} B(st) dt</tex> |
Действительно, | Действительно, | ||
| − | <tex>k! = \ | + | <tex>k! = \int\limits_{0}^{\infty} e^{-t}t^kdt</tex> |
| + | |||
| + | Теперь можно выписать экспоненциальную производящую функцию для треугольника Паскаля: | ||
| + | |||
| + | <tex>\displaystyle\sum\limits_{n, m = 0}^{\infty} \dfrac{1}{(n + m)!} \dbinom{n+m}{m} x^n y^m = \sum\limits_{n = 0}^{\infty} \dfrac{(x + y)^n}{n!} = e^{x + y}</tex> | ||
| + | |||
| + | ==Многочлены Бернулли== | ||
| + | Для начала введём операцию ''усреднения'', положив | ||
| + | |||
| + | <tex>A(f(x)) = \int\limits_{x}^{x+1}f(t)dt</tex>. | ||
| − | + | Нетрудно заметить, что эта операция переводит многочлены в многочлены: она линейна, т.е. <tex>A(a_1f_1 + a_2f_2) = a_1A(f_1) + a_2A(f_2)</tex> для любых постоянных <tex>a_1, a_2</tex> и любых многочленов <tex>f_1, | |
| + | f_2</tex>, а ее значение на мономе<ref>[https://ru.wikipedia.org/wiki/%D0%9E%D0%B4%D0%BD%D0%BE%D1%87%D0%BB%D0%B5%D0%BD Моном]</ref> <tex>x^n</tex> равно | ||
| − | <tex> | + | <tex>A(x^n) = ((x + 1)^{n+1} - x^{n+1}) / (n+1) = x^n + \ldots</tex>, |
| − | + | где многоточие обозначает слагаемые, степени которых меньше <tex>n</tex>. Последняя формула показывает также, что преобразование <tex>A</tex> переводит пространство многочленов степени не выше <tex>n</tex> в себя, а значит, является линейным оператором в этом пространстве. Этот оператор обратим. Действительно, любой многочлен степени не выше <tex>n-1</tex> может быть получен в результате усреднения многочлена такой же степени, и, используя последнюю формулу, мы заключаем, что и любой многочлен степени не выше <tex>n</tex> является результатом усреднения некоторого многочлена степени не выше <tex>n</tex>. Отметим, что при усреднении степень многочлена сохраняется. | |
| − | + | {{Определение | |
| + | |definition= | ||
| + | '''Многочленом Бернулли''' (англ. ''Bernoulli polynomial'') степени <tex>n</tex> называется многочлен <tex>B_n(x)</tex>, результатом усреднения которого служит моном <tex>x^n</tex>, т.е. <tex>B_n(x) = A^{-1}(x^n)</tex>. | ||
| + | }} | ||
| − | + | Первые многочлены Бернулли нетрудно сосчитать: | |
| − | <tex> | + | <tex>B_0(x) = 1</tex> |
| − | + | <tex>B_1(x) = x - \dfrac{1}{2}</tex> | |
| − | <tex> | + | <tex>B_2(x) = x^2 -x + \dfrac{1}{6}</tex> |
| − | + | <tex>B_3(x) = x^3 - \dfrac{3}{2}x^2 + \dfrac{1}{2}x</tex> | |
| − | <tex> | + | <tex>B_4(x) = x^4 - 2x^3 + x^2 - \dfrac{1}{30}</tex> |
| + | |||
| + | <tex>B_5(x) = x^5 - \dfrac{5}{2}x^4 + \dfrac{5}{3}x^3 - \dfrac{1}{6}x</tex> | ||
| + | |||
| + | <tex>B_6(x) = x^6 - 3x^5 + \dfrac{5}{2}x^4 - \dfrac{1}{2}x^2 + \dfrac{1}{42}</tex> | ||
| + | |||
| + | {{Теорема | ||
| + | | about = Экспоненциальная производящая функция для многочленов Бернулли | ||
| + | | statement = | ||
| + | Экспоненциальная производящая функция для многочленов Бернулли имеет вид: | ||
| + | |||
| + | <tex>\mathcal{B}(x, s) = \displaystyle\sum\limits_{n=0}^{\infty}B_n(x)\dfrac{s^n}{n!} = \dfrac{s}{e^s - 1}e^{sx}</tex>. | ||
| + | | proof = | ||
| + | Для доказательства теоремы достаточно применить операцию усреднения к левой и правой частям равенства. С одной стороны, мы имеем: | ||
| + | |||
| + | <tex>A(B(x, s)) = \displaystyle\sum\limits_{n=0}^{\infty}A(B_n(x))\dfrac{s^n}{n!} = \sum\limits_{n=0}^{\infty}x^n\dfrac{s^n}{n!} = e^{xs}</tex>. | ||
| + | |||
| + | С другой стороны, имеем: | ||
| + | |||
| + | <tex>A(\dfrac{s}{e^s - 1}e^{sx}) = \dfrac{s}{e^s-1}A(e^{sx}) = \dfrac{s}{e^s-1}\dfrac{1}{s}(e^{s(x+1)} - e^{sx}) = e^{sx}</tex>, | ||
| + | |||
| + | и теорема доказана. | ||
| + | }} | ||
| + | |||
| + | Определим теперь ''числа Бернулли''<ref>[https://ru.wikipedia.org/wiki/%D0%A7%D0%B8%D1%81%D0%BB%D0%B0_%D0%91%D0%B5%D1%80%D0%BD%D1%83%D0%BB%D0%BB%D0%B8 числа Бернулли]</ref> как значения многочленов Бернулли в нуле. Вот начало последовательности чисел Бернулли: | ||
| + | |||
| + | <tex>1, -\dfrac{1}{2}, 0, \dfrac{1}{6}, -\dfrac{1}{30}, \dfrac{1}{42}, 0, -\dfrac{1}{30}, \dfrac{5}{66}, 0, -\dfrac{691}{2730}, 0, \ldots </tex> | ||
| + | |||
| + | Доказанная теорема позволяет нам легко выписать экспоненциальную производящую функцию для чисел Бернулли. Для этого достаточно подставить в экспоненциальную производящую функцию для многочленов Бернулли значение <tex>x = 0</tex>: | ||
| + | |||
| + | <tex>\displaystyle\sum\limits_{n=0} B_n\dfrac{s^n}{n!} = \dfrac{s}{e^s - 1}</tex>. | ||
==См. также== | ==См. также== | ||
*[[Производящая функция]] | *[[Производящая функция]] | ||
| + | |||
| + | ==Примечания== | ||
| + | <references/> | ||
==Источники информации== | ==Источники информации== | ||
| − | * ''Ландо С.К.'' | + | * ''Ландо С. К.'', Лекции о производящих функциях. {{---}} 3-е изд., испр. {{---}} М.: МЦНМО, 2007. {{---}} 57с. ISBN 978-5-94057-042-4 |
[[Категория: Дискретная математика и алгоритмы]] | [[Категория: Дискретная математика и алгоритмы]] | ||
| − | [[Категория: | + | [[Категория: Производящая функция]] |
| − | |||
Текущая версия на 19:19, 4 сентября 2022
| Определение: |
| Производящие функции нескольких переменных (англ. multivariable generating function) — обычные производящие функции, зависящие более, чем от одной переменной. Очень часто применяются функции от двух переменных (далее они и будут рассматриваться), которые в общем случае принимают вид: . |
Рассмотрим несколько примеров :
Треугольник Паскаля
| Определение: |
| Треугольник Паскаля (англ. Pascal's triangle) — бесконечная таблица биномиальных коэффициентов[1], имеющая треугольную форму. В этом треугольнике на вершине и по бокам стоят единицы. Каждое число равно сумме двух расположенных над ним чисел. |
Элементы треугольника (рис.) перечисляют пути, идущие из его вершины в соответствующую клетку. Пути имеют вид ломаных, составленных из векторов единичной длины двух видов: идущих вправо-вниз и идущих влево-вниз.
Производящая функция может быть сопоставлена треугольнику Паскаля несколькими способами. Например, можно рассмотреть производящую функцию
Второй способ соответствует нумерации элементов треугольника числом отрезков каждого типа на путях, ведущих в соответствующую точку (рис.) . Тогда производящая функция будет иметь вид
Также существует еще один способ: сопоставить треугольнику Паскаля экспоненциальную производящую функцию. Экспоненциальная производящая функция отличается от обычной тем, что в качестве коэффициентов степенного ряда берутся не элементы последовательности , а числа .
Экспоненциальные производящие функции
Зафиксируем произвольную последовательность . Каждой последовательности мы можем сопоставить производящую функцию
определяемую последовательностью . Если в последовательности отсутствуют нулевые элементы, то такое сопоставление взаимно однозначно. До сих пор мы пользовались обычными производящими функциями, отвечающими последовательности . В зависимости от преследуемых целей могут принести и другие последовательности.
| Определение: |
| Производящие экспоненциальные функции (англ. exponential generating function) — функции, соответствующие последовательности . |
| Определение: |
| Экспоненциальные производящие функции для целочисленных последовательностей называют функциями Гурвица (англ. Hurwitz function). |
Чем отличаются экспоненциальные производящие функции от обычных? Посмотрим на поведение экспоненциальных производящих функций при выполнении операции над ними. Сумма ведет себя обычным образом:
а с произведением по-другому:
Коэффициенты произведения вычисляются по формуле
Еще одно существенное отличие экспоненциальных производящих функций от обычных наблюдается при взятии производных и при интегрировании. Дифференцирование или интегрирование экспоненциальной производящей функции приводит к сдвигу последовательности ее коэффициентов без изменения их величины:
Обычная производящая функция выражается через экспоненциальную по формуле
Действительно,
Теперь можно выписать экспоненциальную производящую функцию для треугольника Паскаля:
Многочлены Бернулли
Для начала введём операцию усреднения, положив
.
Нетрудно заметить, что эта операция переводит многочлены в многочлены: она линейна, т.е. для любых постоянных и любых многочленов , а ее значение на мономе[2] равно
,
где многоточие обозначает слагаемые, степени которых меньше . Последняя формула показывает также, что преобразование переводит пространство многочленов степени не выше в себя, а значит, является линейным оператором в этом пространстве. Этот оператор обратим. Действительно, любой многочлен степени не выше может быть получен в результате усреднения многочлена такой же степени, и, используя последнюю формулу, мы заключаем, что и любой многочлен степени не выше является результатом усреднения некоторого многочлена степени не выше . Отметим, что при усреднении степень многочлена сохраняется.
| Определение: |
| Многочленом Бернулли (англ. Bernoulli polynomial) степени называется многочлен , результатом усреднения которого служит моном , т.е. . |
Первые многочлены Бернулли нетрудно сосчитать:
| Теорема (Экспоненциальная производящая функция для многочленов Бернулли): |
Экспоненциальная производящая функция для многочленов Бернулли имеет вид:
. |
| Доказательство: |
|
Для доказательства теоремы достаточно применить операцию усреднения к левой и правой частям равенства. С одной стороны, мы имеем: . С другой стороны, имеем: , и теорема доказана. |
Определим теперь числа Бернулли[3] как значения многочленов Бернулли в нуле. Вот начало последовательности чисел Бернулли:
Доказанная теорема позволяет нам легко выписать экспоненциальную производящую функцию для чисел Бернулли. Для этого достаточно подставить в экспоненциальную производящую функцию для многочленов Бернулли значение :
.
См. также
Примечания
Источники информации
- Ландо С. К., Лекции о производящих функциях. — 3-е изд., испр. — М.: МЦНМО, 2007. — 57с. ISBN 978-5-94057-042-4