Скрытые Марковские модели — различия между версиями
Paul1298 (обсуждение | вклад) м |
м (rollbackEdits.php mass rollback) |
||
| (не показано 15 промежуточных версий 2 участников) | |||
| Строка 6: | Строка 6: | ||
==Описание== | ==Описание== | ||
| − | Модель представляет из себя [[Марковская цепь|марковскую цепь]], для которой нам известны начальная вероятность и матрица вероятностей переходов. Скрытой она называется потому, что мы не имеем информации о ее текущем состоянии. Мы получаем информацию на основе некоторого наблюдения, в рассмотренном ниже алгоритме мы будем использовать просто натуральное число от 1 до <tex>N</tex>, как индекс наблюдаемого события. Для каждого состояния скрытой марковской модели задан вектор вероятности эмиссии, который характеризует вероятность наблюдения каждого события, когда модель находится в этом состоянии. Совокупность таких векторов образует матрицу эмиссии. | + | Модель представляет из себя [[Марковская цепь|марковскую цепь]], для которой нам известны начальная вероятность и матрица вероятностей переходов. Скрытой она называется потому, что мы не имеем информации о ее текущем состоянии. Мы получаем информацию на основе некоторого наблюдения, в рассмотренном ниже алгоритме мы будем использовать просто натуральное число от <tex>1</tex> до <tex>N</tex>, как индекс наблюдаемого события. Для каждого состояния скрытой марковской модели задан вектор вероятности эмиссии, который характеризует вероятность наблюдения каждого события, когда модель находится в этом состоянии. Совокупность таких векторов образует матрицу эмиссии. |
Марковская модель <tex>\lambda</tex> задается как <tex>\lambda = \{S, \Omega, \Pi, A, B\}</tex>, где <tex>S = \{s_1 \dots s_n\}</tex> {{---}} состояния, <tex>\Omega = \{\omega_1 \dots \omega_m\}</tex> {{---}} возможные события, <tex>\Pi = \{\pi_1 \dots \pi_n\}</tex> {{---}} начальные вероятности, <tex>A = \{a_{ij}\}</tex> {{---}} матрица переходов, а <tex>B = \{b_{i\omega_k}\}</tex> {{---}} вероятность наблюдения события <tex>\omega_k</tex> после перехода в состояние <tex>s_i</tex>. | Марковская модель <tex>\lambda</tex> задается как <tex>\lambda = \{S, \Omega, \Pi, A, B\}</tex>, где <tex>S = \{s_1 \dots s_n\}</tex> {{---}} состояния, <tex>\Omega = \{\omega_1 \dots \omega_m\}</tex> {{---}} возможные события, <tex>\Pi = \{\pi_1 \dots \pi_n\}</tex> {{---}} начальные вероятности, <tex>A = \{a_{ij}\}</tex> {{---}} матрица переходов, а <tex>B = \{b_{i\omega_k}\}</tex> {{---}} вероятность наблюдения события <tex>\omega_k</tex> после перехода в состояние <tex>s_i</tex>. | ||
== Примеры == | == Примеры == | ||
| − | [[Файл: | + | [[Файл:СММ_пример.png|500px|thumb|right|Пример СММ]] |
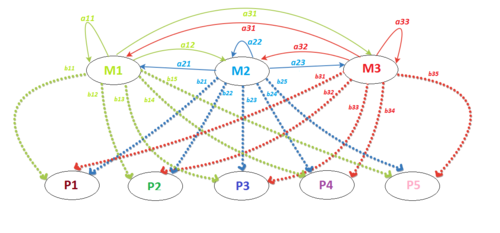
Рассмотрим пример скрытой марковской модели. У Деда Мороза есть три мешка с подарками в разноцветной упаковке: красной, синей, зеленой и фиолетовой. Ночью Дед Мороз пробирается в квартиру и тайком выкладывает подарки под елкой в ряд, доставая по одному подарку из мешка. Наутро мы обнаруживаем упорядоченную последовательность из пяти подарков и хотим сделать наилучшее предположение о последовательности мешков, из которых он доставал эти подарки. | Рассмотрим пример скрытой марковской модели. У Деда Мороза есть три мешка с подарками в разноцветной упаковке: красной, синей, зеленой и фиолетовой. Ночью Дед Мороз пробирается в квартиру и тайком выкладывает подарки под елкой в ряд, доставая по одному подарку из мешка. Наутро мы обнаруживаем упорядоченную последовательность из пяти подарков и хотим сделать наилучшее предположение о последовательности мешков, из которых он доставал эти подарки. | ||
| − | Дед Мороз с мешками {{---}} скрытая марковская модель. При этом 4 цвета {{---}} пространство из <tex>M</tex> возможных событий, 3 мешка {{---}} количество состояний <tex>N</tex>, 5 подарков {{---}} наши <tex>K</tex> наблюдений, каждое из которых представлено цифрой {{---}} номером цвета {{---}} от 1 до 5. Мы знаем, каковы вероятности того, что Дед Мороз начнет доставать подарки из мешка с номером <tex>i</tex> {{---}} вектор <tex>\pi[i]</tex>. Мы также знаем матрицу переходов <tex>A</tex>, какова вероятность того, что от мешка с номером <tex>i</tex> Дед Мороз переходит к мешку с номером <tex>j</tex>. Мешки Деда Мороза бесконечны, но мы точно знаем, каково соотношение цветов подарков в каждом мешке ему загрузили на заводе в Великом Устюге. Это матрица вероятностей эмиссии <tex>B</tex>. | + | Дед Мороз с мешками {{---}} скрытая марковская модель. При этом <tex>4</tex> цвета {{---}} пространство из <tex>M</tex> возможных событий, <tex>3</tex> мешка {{---}} количество состояний <tex>N</tex>, <tex>5</tex> подарков {{---}} наши <tex>K</tex> наблюдений, каждое из которых представлено цифрой {{---}} номером цвета {{---}} от <tex>1</tex> до <tex>5</tex>. Мы знаем, каковы вероятности того, что Дед Мороз начнет доставать подарки из мешка с номером <tex>i</tex> {{---}} вектор <tex>\pi[i]</tex>. Мы также знаем матрицу переходов <tex>A</tex>, какова вероятность того, что от мешка с номером <tex>i</tex> Дед Мороз переходит к мешку с номером <tex>j</tex>. Мешки Деда Мороза бесконечны, но мы точно знаем, каково соотношение цветов подарков в каждом мешке ему загрузили на заводе в Великом Устюге. Это матрица вероятностей эмиссии <tex>B</tex>. |
== Алгоритмы на СММ == | == Алгоритмы на СММ == | ||
| + | [[Файл:Kernel_Machine.svg.png|250px|right]] | ||
| + | * Кластерный анализ (англ. ''Cluster analysis'')<ref>[https://ru.wikipedia.org/wiki/%D0%9A%D0%BB%D0%B0%D1%81%D1%82%D0%B5%D1%80%D0%BD%D1%8B%D0%B9_%D0%B0%D0%BD%D0%B0%D0%BB%D0%B8%D0%B7 Кластерный анализ]</ref> {{---}} многомерная статистическая процедура, выполняющая сбор данных, содержащих информацию о выборке объектов, и затем упорядочивающая объекты в сравнительно однородные группы. | ||
| + | [[Файл:Linear_regression.svg.png|250px|thumb|right|Регрессионный анализ]] | ||
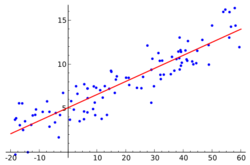
| + | *Регрессионный анализ (англ. ''Regression analysis'')<ref>[https://ru.wikipedia.org/wiki/%D0%A0%D0%B5%D0%B3%D1%80%D0%B5%D1%81%D1%81%D0%B8%D0%BE%D0%BD%D0%BD%D1%8B%D0%B9_%D0%B0%D0%BD%D0%B0%D0%BB%D0%B8%D0%B7 Регрессионный анализ]</ref> {{---}} статистический метод исследования влияния одной или нескольких независимых переменных <tex>X_1, X_2 \dots X_p</tex> на зависимую переменную <tex>Y</tex>. | ||
| + | * Задача классифика́ции (англ. ''Statistical classification'')<ref>[https://ru.wikipedia.org/wiki/%D0%97%D0%B0%D0%B4%D0%B0%D1%87%D0%B0_%D0%BA%D0%BB%D0%B0%D1%81%D1%81%D0%B8%D1%84%D0%B8%D0%BA%D0%B0%D1%86%D0%B8%D0%B8 Задача классификации]</ref> {{---}} формализованная задача, в которой имеется множество объектов (ситуаций), разделённых некоторым образом на классы. | ||
| + | |||
| + | ==Обучение== | ||
| + | Параметр задачи обучения СММ {{---}} это нахождение лучшего результата. Пусть дана выходная последовательность или множество таких последовательностей,лучший набор состояний переходов и вероятности эмиссии. Задача, как правило, для получения максимальной вероятностной оценки параметров СММ, учитывая множество выходных последовательностей. Не существует общего решения этой задачи, но для нахождения локального максимально правдоподобного результата может быть эффективно использован [[Алгоритм Баума-Велша]]. Если же СММ используется для прогнозирования временных рядов, то можно использовать более изощренный метод, такой как Марковская цепь Монте-Карло<ref>[https://en.wikipedia.org/wiki/Markov_chain_Monte_Carlo Markov chain Monte Carlo(МСМС)]</ref>, что оказалось благоприятным для нахождения одной модели вероятности как с точки зрения точности, так и стабильности<ref>Sipos, I. Róbert. Parallel stratified MCMC sampling of AR-HMMs for stochastic time series prediction. In: Proceedings, 4th Stochastic Modeling Techniques and Data Analysis International Conference with Demographics Workshop (SMTDA2016), pp. 295-306. Valletta, 2016.[http://1drv.ms/b/s!ApL_0Av0YGDLglwEOv1aYAGbmQeL PDF]</ref>. Поскольку в МЦМК возникают значительные вычислительные нагрузки, то в случаях, когда вычислительная масштабируемость представляет также интерес, можно также прибегнуть к вариационной аппроксимации Байесовского вывода<ref>[https://ru.wikipedia.org/wiki/%D0%91%D0%B0%D0%B9%D0%B5%D1%81%D0%BE%D0%B2%D1%81%D0%BA%D0%B8%D0%B9_%D0%B2%D1%8B%D0%B2%D0%BE%D0%B4 Байесовский вывод]</ref><ref>Sotirios P. Chatzis, Dimitrios Kosmopoulos, “A Variational Bayesian Methodology for Hidden Markov Models utilizing Student’s-t Mixtures,” Pattern Recognition, vol. 44, no. 2, pp. 295-306, Feb. 2011. [http://www.sciencedirect.com/science/article/pii/S0031320310004383]</ref>. Действительно, приближенный вариационный вывод предлагает вычислительную эффективность, сравнимую с максимизацией ожидания,ведь пока производящий профиль точности лишь немного уступает точной МЦМК-типа Байесовского вывода. | ||
| + | |||
| + | ==См. также== | ||
* [[Алгоритм Витерби]] {{---}} делает наилучшее предположение о последовательности состояний скрытой модели на основе последовательности наблюдений. | * [[Алгоритм Витерби]] {{---}} делает наилучшее предположение о последовательности состояний скрытой модели на основе последовательности наблюдений. | ||
* [[Алгоритм "Вперед-Назад"]] {{---}} находит вероятность попадания в состояние <tex>s_n</tex> на <tex>t</tex>-ом шаге. | * [[Алгоритм "Вперед-Назад"]] {{---}} находит вероятность попадания в состояние <tex>s_n</tex> на <tex>t</tex>-ом шаге. | ||
* [[Алгоритм Баума-Велша]] {{---}} меняет <tex>a_{ij}</tex>, максимизируя вероятность наблюдения последовательности событий <tex>O</tex>. | * [[Алгоритм Баума-Велша]] {{---}} меняет <tex>a_{ij}</tex>, максимизируя вероятность наблюдения последовательности событий <tex>O</tex>. | ||
| + | |||
| + | ==Примечания== | ||
| + | <references/> | ||
== Источники информации == | == Источники информации == | ||
Текущая версия на 19:19, 4 сентября 2022
| Определение: |
| Скрытая Марковская модель (англ. A hidden Markov model) — модель процесса, в которой процесс считается Марковским, причем неизвестно, в каком состоянии находится система (состояния скрыты), но каждое состояние может с некоторой вероятностью произвести событие , которое можно наблюдать. |
Описание
Модель представляет из себя марковскую цепь, для которой нам известны начальная вероятность и матрица вероятностей переходов. Скрытой она называется потому, что мы не имеем информации о ее текущем состоянии. Мы получаем информацию на основе некоторого наблюдения, в рассмотренном ниже алгоритме мы будем использовать просто натуральное число от до , как индекс наблюдаемого события. Для каждого состояния скрытой марковской модели задан вектор вероятности эмиссии, который характеризует вероятность наблюдения каждого события, когда модель находится в этом состоянии. Совокупность таких векторов образует матрицу эмиссии.
Марковская модель задается как , где — состояния, — возможные события, — начальные вероятности, — матрица переходов, а — вероятность наблюдения события после перехода в состояние .
Примеры
Рассмотрим пример скрытой марковской модели. У Деда Мороза есть три мешка с подарками в разноцветной упаковке: красной, синей, зеленой и фиолетовой. Ночью Дед Мороз пробирается в квартиру и тайком выкладывает подарки под елкой в ряд, доставая по одному подарку из мешка. Наутро мы обнаруживаем упорядоченную последовательность из пяти подарков и хотим сделать наилучшее предположение о последовательности мешков, из которых он доставал эти подарки. Дед Мороз с мешками — скрытая марковская модель. При этом цвета — пространство из возможных событий, мешка — количество состояний , подарков — наши наблюдений, каждое из которых представлено цифрой — номером цвета — от до . Мы знаем, каковы вероятности того, что Дед Мороз начнет доставать подарки из мешка с номером — вектор . Мы также знаем матрицу переходов , какова вероятность того, что от мешка с номером Дед Мороз переходит к мешку с номером . Мешки Деда Мороза бесконечны, но мы точно знаем, каково соотношение цветов подарков в каждом мешке ему загрузили на заводе в Великом Устюге. Это матрица вероятностей эмиссии .
Алгоритмы на СММ
- Кластерный анализ (англ. Cluster analysis)[1] — многомерная статистическая процедура, выполняющая сбор данных, содержащих информацию о выборке объектов, и затем упорядочивающая объекты в сравнительно однородные группы.
- Регрессионный анализ (англ. Regression analysis)[2] — статистический метод исследования влияния одной или нескольких независимых переменных на зависимую переменную .
- Задача классифика́ции (англ. Statistical classification)[3] — формализованная задача, в которой имеется множество объектов (ситуаций), разделённых некоторым образом на классы.
Обучение
Параметр задачи обучения СММ — это нахождение лучшего результата. Пусть дана выходная последовательность или множество таких последовательностей,лучший набор состояний переходов и вероятности эмиссии. Задача, как правило, для получения максимальной вероятностной оценки параметров СММ, учитывая множество выходных последовательностей. Не существует общего решения этой задачи, но для нахождения локального максимально правдоподобного результата может быть эффективно использован Алгоритм Баума-Велша. Если же СММ используется для прогнозирования временных рядов, то можно использовать более изощренный метод, такой как Марковская цепь Монте-Карло[4], что оказалось благоприятным для нахождения одной модели вероятности как с точки зрения точности, так и стабильности[5]. Поскольку в МЦМК возникают значительные вычислительные нагрузки, то в случаях, когда вычислительная масштабируемость представляет также интерес, можно также прибегнуть к вариационной аппроксимации Байесовского вывода[6][7]. Действительно, приближенный вариационный вывод предлагает вычислительную эффективность, сравнимую с максимизацией ожидания,ведь пока производящий профиль точности лишь немного уступает точной МЦМК-типа Байесовского вывода.
См. также
- Алгоритм Витерби — делает наилучшее предположение о последовательности состояний скрытой модели на основе последовательности наблюдений.
- Алгоритм "Вперед-Назад" — находит вероятность попадания в состояние на -ом шаге.
- Алгоритм Баума-Велша — меняет , максимизируя вероятность наблюдения последовательности событий .
Примечания
- ↑ Кластерный анализ
- ↑ Регрессионный анализ
- ↑ Задача классификации
- ↑ Markov chain Monte Carlo(МСМС)
- ↑ Sipos, I. Róbert. Parallel stratified MCMC sampling of AR-HMMs for stochastic time series prediction. In: Proceedings, 4th Stochastic Modeling Techniques and Data Analysis International Conference with Demographics Workshop (SMTDA2016), pp. 295-306. Valletta, 2016.PDF
- ↑ Байесовский вывод
- ↑ Sotirios P. Chatzis, Dimitrios Kosmopoulos, “A Variational Bayesian Methodology for Hidden Markov Models utilizing Student’s-t Mixtures,” Pattern Recognition, vol. 44, no. 2, pp. 295-306, Feb. 2011. [1]