Задача о динамической связности — различия между версиями
(→add(u,v)) |
м (rollbackEdits.php mass rollback) |
||
| (не показано 76 промежуточных версий 3 участников) | |||
| Строка 6: | Строка 6: | ||
}} | }} | ||
== Динамическая связность в лесах == | == Динамическая связность в лесах == | ||
| − | Если задача такова, что в графе нет и не может быть циклов, то она сводится к задаче о связности в [[Деревья Эйлерова обхода|деревьях эйлерова обхода]]. Время работы каждого запроса для упрощённой задачи {{---}} <tex>O(\log n)</tex>. | + | Если задача такова, что в графе нет и не может быть циклов, то она сводится к задаче о связности в [[Деревья Эйлерова обхода|деревьях эйлерова обхода]]. Время работы каждого запроса для упрощённой задачи {{---}} <tex>O(\log n)</tex>, где <tex>n</tex> {{---}} количество вершин в графе. |
| + | |||
== Обобщение задачи для произвольных графов == | == Обобщение задачи для произвольных графов == | ||
Существуют задачи, в которых граф не обязательно на протяжении нашей работы после каждой операции добавления ребра остаётся лесом. Для решения таких задач в каждой компоненте связности выделим [[Остовные деревья: определения, лемма о безопасном ребре|остовные деревья]], которые образуют остовный лес. | Существуют задачи, в которых граф не обязательно на протяжении нашей работы после каждой операции добавления ребра остаётся лесом. Для решения таких задач в каждой компоненте связности выделим [[Остовные деревья: определения, лемма о безопасном ребре|остовные деревья]], которые образуют остовный лес. | ||
| − | |||
| − | |||
| − | |||
| − | |||
| + | [[Файл:Graph.jpg|530px|thumb|left|Граф]] [[Файл:Spanforest.jpg|530px|thumb|right|Остовный лес в графе]] | ||
| Строка 31: | Строка 29: | ||
| − | === | + | ===Проверка связности=== |
Граф и его остовный лес {{---}} одно и то же с точки зрения связности. Поэтому проверка связности в графе сводится к проверке связности в остовном лесе и решается за <tex>O(\log n)</tex>.<!--Добавление рёбер можно рассмотреть с точки зрения [[СНМ (реализация с помощью леса корневых деревьев)|системы непересекающихся множеств]], такой запрос будет работать за <tex>O(\log n)</tex>. Операция проверки сводится к проверке связности в остовном лесе и работает также за <tex>O(\log n)</tex>.--> | Граф и его остовный лес {{---}} одно и то же с точки зрения связности. Поэтому проверка связности в графе сводится к проверке связности в остовном лесе и решается за <tex>O(\log n)</tex>.<!--Добавление рёбер можно рассмотреть с точки зрения [[СНМ (реализация с помощью леса корневых деревьев)|системы непересекающихся множеств]], такой запрос будет работать за <tex>O(\log n)</tex>. Операция проверки сводится к проверке связности в остовном лесе и работает также за <tex>O(\log n)</tex>.--> | ||
| − | === | + | ===Добавление ребра=== |
Чтобы разобраться с тем, как изменится граф и остовный лес при добавлении и удалении ребра, введём функцию <tex>l(e):E{\rightarrow}[0;\log n]</tex> и назовём её ''уровнем ребра'' <tex>e</tex>. Уровни ребра можно распределить любым способом, но для всех <tex> i </tex> должно выполняться следующее свойство: размер каждой компоненты связности <tex>G_i</tex> не превосходит <tex>\dfrac{n}{2^i}</tex>. Здесь графы <tex>G_i</tex> определяются так: <tex>G_i=\langle V, E\rangle: \{e \in E \mid l(e) \geqslant i\}</tex>. | Чтобы разобраться с тем, как изменится граф и остовный лес при добавлении и удалении ребра, введём функцию <tex>l(e):E{\rightarrow}[0;\log n]</tex> и назовём её ''уровнем ребра'' <tex>e</tex>. Уровни ребра можно распределить любым способом, но для всех <tex> i </tex> должно выполняться следующее свойство: размер каждой компоненты связности <tex>G_i</tex> не превосходит <tex>\dfrac{n}{2^i}</tex>. Здесь графы <tex>G_i</tex> определяются так: <tex>G_i=\langle V, E\rangle: \{e \in E \mid l(e) \geqslant i\}</tex>. | ||
| Строка 43: | Строка 41: | ||
====Псевдокод==== | ====Псевдокод==== | ||
| − | '''function''' add('''Node''' u, '''Node''' v) | + | '''function''' <tex>\mathrm{add}</tex>('''Node''' u, '''Node''' v): |
| − | e = < | + | '''Edge''' e = <tex>\langle </tex>u, v<tex>\rangle</tex> |
| − | + | e.level = 0 | |
| − | + | <tex>G_0</tex> = <tex>G_0</tex> <tex>\cup</tex> e<!---insert(<tex>G_0</tex>, e)--> | |
| − | + | '''if not''' <tex>\mathrm{connected(u,v)}</tex> | |
| + | <tex>F_0</tex> = <tex>F_0</tex> <tex>\cup</tex> e<!---insert(<tex>F_0</tex>, e)--> | ||
| − | === | + | ===Удаление ребра=== |
{{Утверждение | {{Утверждение | ||
|statement=Если ребро, которое мы хотим удалить, не принадлежит остовному лесу, то связность между любой парой вершин сохранится. | |statement=Если ребро, которое мы хотим удалить, не принадлежит остовному лесу, то связность между любой парой вершин сохранится. | ||
| Строка 55: | Строка 54: | ||
Предположим, что нарушилась связность для каких-то двух вершин. Значит, мы убрали мост. А любой мост принадлежит всем остовным деревьям его компоненты. Противоречие. | Предположим, что нарушилась связность для каких-то двух вершин. Значит, мы убрали мост. А любой мост принадлежит всем остовным деревьям его компоненты. Противоречие. | ||
}} | }} | ||
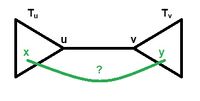
| − | [[Файл:Is_there_xy.jpg|200px|thumb|right]] | + | [[Файл:Is_there_xy.jpg|200px|thumb|right|Компонента связности T.]] |
Таким образом, если мы удалили ребро не из остовного леса, то нам не придётся перестраивать лес и пересчитывать значение <tex>\mathrm{connected(u,v)}</tex>. | Таким образом, если мы удалили ребро не из остовного леса, то нам не придётся перестраивать лес и пересчитывать значение <tex>\mathrm{connected(u,v)}</tex>. | ||
| − | Рассмотрим случаи, когда мы берём ребро из леса. Тогда необходимо выяснить, | + | |
| + | Рассмотрим случаи, когда мы берём ребро из леса. Тогда необходимо выяснить, является ли данное ребро мостом в графе, и выполнить соответствующие действия. | ||
Проверим, является ли ребро мостом. У ребра <tex>uv</tex> известен уровень, пусть он равен <tex>i</tex>. Попробуем найти другое ребро (<tex>xy</tex>), соединяющее поддеревья <tex>T_u</tex> и <tex>T_v</tex>, на которые распалось остовное дерево исследуемой компоненты <tex>T</tex>. | Проверим, является ли ребро мостом. У ребра <tex>uv</tex> известен уровень, пусть он равен <tex>i</tex>. Попробуем найти другое ребро (<tex>xy</tex>), соединяющее поддеревья <tex>T_u</tex> и <tex>T_v</tex>, на которые распалось остовное дерево исследуемой компоненты <tex>T</tex>. | ||
{{Утверждение | {{Утверждение | ||
| − | |statement=<tex> | + | |statement=Если ребро <tex>xy</tex> существует, то его уровень не больше <tex>i</tex>. |
| − | |proof=От противного. Пусть <tex>l(xy)=j</tex> | + | |proof=От противного. Пусть <tex>l(xy)=j</tex>, где <tex>j > i</tex>. Тогда вершины <tex>x</tex> и <tex>y</tex> каким-то образом связаны в <tex>F_j</tex> (либо непосредственно ребром <tex>xy</tex>, либо каким-то другим путём). Но <tex>F_j \subseteq F_i</tex>. Значит, в <tex>F_i</tex> между <tex>x</tex> и <tex>y</tex> сохранился путь из рёбер уровня не меньше <tex>j</tex> и появился другой путь через <tex>uv</tex>. Приходим к противоречию, так как в <tex>F_i</tex> все компоненты должны быть деревьями. |
}} | }} | ||
| − | Чтобы найти <tex>xy</tex>, выберем из поддеревьев <tex>T_u</tex> и <tex>T_v</tex> наименьшее. Не умаляя общности, будем считать, что <tex>| | + | Чтобы найти <tex>xy</tex>, выберем из поддеревьев <tex>T_u</tex> и <tex>T_v</tex> наименьшее. Не умаляя общности, будем считать, что <tex>|T_u|\leqslant|T_v|</tex>. <!--ежу понятно--> Так как всегда из двух слагаемых можно выбрать одно такое, что оно не превосходит половины их суммы, имеем важное свойство: <tex>|T_u|\leqslant\dfrac{|T_u|+|T_v|}{2}=\dfrac{|T|}{2}</tex>. Также нам известно, что <tex>T \subseteq F_i</tex>, а значит, <tex>|T|\leqslant\dfrac{n}{2^i}</tex>. Отсюда <tex>|T_u|\leqslant\dfrac{n}{2^{i+1}}</tex>. Это неравенство позволит нам увеличивать уровни рёбер при необходимости. |
| − | + | Будем искать ребро <tex>xy</tex> следующим образом: | |
| − | # Если | + | # Выбираем любое ребро уровня <tex>i</tex>, выходящее из вершины, принадлежащей <tex>T_u</tex>. |
| − | # Если | + | # Если выбранное ребро ведёт в <tex>T_v</tex>, выходим из цикла и добавляем ребро <tex>xy</tex> в остовные леса <tex>F_i</tex>, для которых <tex>i\leqslant l(xy)</tex> и выходим из цикла; |
| − | # Если есть непроверенные рёбра, переходим к пункту <tex>1</tex>; | + | # Если выбранное ребро ведёт в другую вершину поддерева <tex>T_u</tex>, увеличиваем его уровень на <tex>1</tex>; |
| − | # Если таких рёбер уровня <tex>i</tex> не осталось и <tex>i>0</tex>, | + | # Если есть непроверенные рёбра на интересующем нас уровне <tex>i</tex>, переходим к пункту <tex>1</tex>; |
| + | # Если таких рёбер уровня <tex>i</tex> не осталось и <tex>i>0</tex>, рассматриваем уровень на единицу меньший и переходим к пункту <tex>1</tex>; | ||
# Если все рёбра просканированы и <tex>i=0</tex>, то <tex>uv</tex> является мостом. | # Если все рёбра просканированы и <tex>i=0</tex>, то <tex>uv</tex> является мостом. | ||
'''Замечание.''' Увеличив уровень ребра на единицу, нужно не забыть обновить <tex>G_{i+1}</tex> и <tex>F_{i+1}</tex>. | '''Замечание.''' Увеличив уровень ребра на единицу, нужно не забыть обновить <tex>G_{i+1}</tex> и <tex>F_{i+1}</tex>. | ||
| + | ====Оценка времени работы==== | ||
| + | Пункт <tex>2</tex> работает за <tex>O(\log^2 n)</tex>, так как после выхода из цикла мы добавляем ребро за <tex>O(\log n)</tex> на каждом уровне, а количество уровней не больше <tex>\log n</tex>. | ||
| + | <!--5 сек, тут кажись я права всё-таки, нужен Лёха--> | ||
| + | |||
| + | Пусть до момента, когда мы нашли нужное ребро, мы сделали <tex>S</tex> неудачных сканирований. После каждого такого сканирования нам приходится добавлять новые рёбра в <tex>G_{i+1}</tex>, что стоит <tex>O(\log n)</tex>. Получаем сложность удаления одного ребра <tex>O(\log^2{n}+S\cdot\log n)</tex>. <!--- Возможно, мы удалим мост, но это уже другая история, да и она всяко лучше логарифмов в квадрате... ---> | ||
| + | |||
| + | Выразим сложность одной операции <tex>\mathrm{remove}</tex> другим способом. Для <tex>n</tex> вершин и <tex>m</tex> вызовов процедуры сложность равна <tex>O(\log^2{n}\cdot m+\log n\cdot\displaystyle \sum_{i=1}^m S_i)</tex>, что не превосходит <tex>O(\log^2{n} \cdot m+\log n\cdot\log n\cdot m)</tex>, так как уровень ребра <tex>m</tex> раз рос максимум до <tex>\log n</tex>. Отсюда суммарная сложность всех запросов равна <tex>O(\log^2{n}\cdot m)</tex>, а для одного запроса мы решаем задачу за <tex>O(\log^2{n})</tex>. | ||
====Псевдокод==== | ====Псевдокод==== | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | '''function''' <tex>\mathrm{remove}</tex>('''Node''' u, '''Node''' v): | |
| + | '''Edge''' e = <tex>\langle </tex>u, v<tex>\rangle</tex> | ||
| + | '''for''' i = e.level '''downto''' 0 | ||
| + | <tex>G_i</tex> = <tex>G_i\setminus</tex>e<!---delete(<tex>G_i</tex>, e)---> | ||
| + | <tex>F_i</tex> = <tex>F_i\setminus</tex>e<!---delete(<tex>F_i</tex>, e)---> | ||
| + | '''Edge''' e2 | ||
| + | '''for''' e2 = <tex>\langle </tex>x, y<tex>\rangle</tex> : e2.level == i '''and''' x <tex>\in T_u</tex> | ||
| + | '''if''' y <tex>\in T_v</tex> | ||
| + | '''for''' j = i '''downto''' 0 | ||
| + | <tex>F_j</tex> = <tex>F_j</tex> <tex>\cup</tex> e2<!---insert(<tex>F_i</tex>, e2)--> | ||
| + | '''return''' | ||
| + | '''else''' | ||
| + | e2.level++ | ||
| + | <tex>G_{i+1}</tex> = <tex>G_{i+1}</tex> <tex>\cup</tex> e2<!---insert(<tex>F_i</tex>, e2)--> | ||
== См. также == | == См. также == | ||
Текущая версия на 19:15, 4 сентября 2022
| Задача: |
Есть неориентированный граф из вершин, изначально не содержащий рёбер. Требуется обработать запросов трёх типов:
|
Содержание
Динамическая связность в лесах
Если задача такова, что в графе нет и не может быть циклов, то она сводится к задаче о связности в деревьях эйлерова обхода. Время работы каждого запроса для упрощённой задачи — , где — количество вершин в графе.
Обобщение задачи для произвольных графов
Существуют задачи, в которых граф не обязательно на протяжении нашей работы после каждой операции добавления ребра остаётся лесом. Для решения таких задач в каждой компоненте связности выделим остовные деревья, которые образуют остовный лес.
Проверка связности
Граф и его остовный лес — одно и то же с точки зрения связности. Поэтому проверка связности в графе сводится к проверке связности в остовном лесе и решается за .
Добавление ребра
Чтобы разобраться с тем, как изменится граф и остовный лес при добавлении и удалении ребра, введём функцию и назовём её уровнем ребра . Уровни ребра можно распределить любым способом, но для всех должно выполняться следующее свойство: размер каждой компоненты связности не превосходит . Здесь графы определяются так: .
Очевидно, что . Выделим в графах остовные леса таким образом, что , где — остовный лес графа .
Удобнее всего новому ребру давать уровень . В этом случае изменится только , так как в остальные подграфы рёбра нулевого уровня не входят. После вставки нового ребра нам нужно проверить, были ли вершины и в одной компоненте связности до того, как мы вставили ребро. Если они лежали в разных компонентах, то необходимо новое ребро добавить и в остовный лес .
Псевдокод
function (Node u, Node v): Edge e = u, v e.level = 0 = e if not = e
Удаление ребра
| Утверждение: |
Если ребро, которое мы хотим удалить, не принадлежит остовному лесу, то связность между любой парой вершин сохранится. |
|
Докажем от противного. Допустим, что это не так. Понятно, что при разрезании ребра нового пути между вершинами не появится. Предположим, что нарушилась связность для каких-то двух вершин. Значит, мы убрали мост. А любой мост принадлежит всем остовным деревьям его компоненты. Противоречие. |
Таким образом, если мы удалили ребро не из остовного леса, то нам не придётся перестраивать лес и пересчитывать значение .
Рассмотрим случаи, когда мы берём ребро из леса. Тогда необходимо выяснить, является ли данное ребро мостом в графе, и выполнить соответствующие действия.
Проверим, является ли ребро мостом. У ребра известен уровень, пусть он равен . Попробуем найти другое ребро (), соединяющее поддеревья и , на которые распалось остовное дерево исследуемой компоненты .
| Утверждение: |
Если ребро существует, то его уровень не больше . |
| От противного. Пусть , где . Тогда вершины и каким-то образом связаны в (либо непосредственно ребром , либо каким-то другим путём). Но . Значит, в между и сохранился путь из рёбер уровня не меньше и появился другой путь через . Приходим к противоречию, так как в все компоненты должны быть деревьями. |
Чтобы найти , выберем из поддеревьев и наименьшее. Не умаляя общности, будем считать, что . Так как всегда из двух слагаемых можно выбрать одно такое, что оно не превосходит половины их суммы, имеем важное свойство: . Также нам известно, что , а значит, . Отсюда . Это неравенство позволит нам увеличивать уровни рёбер при необходимости.
Будем искать ребро следующим образом:
- Выбираем любое ребро уровня , выходящее из вершины, принадлежащей .
- Если выбранное ребро ведёт в , выходим из цикла и добавляем ребро в остовные леса , для которых и выходим из цикла;
- Если выбранное ребро ведёт в другую вершину поддерева , увеличиваем его уровень на ;
- Если есть непроверенные рёбра на интересующем нас уровне , переходим к пункту ;
- Если таких рёбер уровня не осталось и , рассматриваем уровень на единицу меньший и переходим к пункту ;
- Если все рёбра просканированы и , то является мостом.
Замечание. Увеличив уровень ребра на единицу, нужно не забыть обновить и .
Оценка времени работы
Пункт работает за , так как после выхода из цикла мы добавляем ребро за на каждом уровне, а количество уровней не больше .
Пусть до момента, когда мы нашли нужное ребро, мы сделали неудачных сканирований. После каждого такого сканирования нам приходится добавлять новые рёбра в , что стоит . Получаем сложность удаления одного ребра .
Выразим сложность одной операции другим способом. Для вершин и вызовов процедуры сложность равна , что не превосходит , так как уровень ребра раз рос максимум до . Отсюда суммарная сложность всех запросов равна , а для одного запроса мы решаем задачу за .
Псевдокод
function (Node u, Node v): Edge e = u, v for i = e.level downto 0 = e = e Edge e2 for e2 = x, y : e2.level == i and x if y for j = i downto 0 = e2 return else e2.level++ = e2