Полиномиальная иерархия — различия между версиями
м (rollbackEdits.php mass rollback) |
|||
| (не показано 13 промежуточных версий 5 участников) | |||
| Строка 1: | Строка 1: | ||
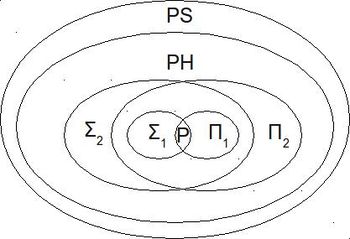
| − | Полиномиальная иерархия - иерархия классов сложности, которая обобщает классы [[Класс P|P]], [[Класс NP|NP]] и [[Класс coNP|coNP]] до вычислений с оракулом. | + | Полиномиальная иерархия - иерархия классов сложности, которая обобщает классы [[Класс P|P]], [[Класс NP|NP]] и [[Класс coNP|coNP]] до вычислений с оракулом.[[Файл:Ph_diagram.jpg|thumb|350px|Отношения классов полиномиальной иерархии]] |
| − | + | ==Классы из полиномиальной иерархии== | |
| + | Приведем некоторые соотношения между классами [[Классы Sigma_i и Pi_i|<math>\Sigma_i</math> и <math>\Pi_i</math>]]. | ||
| + | <tex>\Sigma_0 = P</tex><br> | ||
| + | <tex>\Sigma_1 = NP</tex><br> | ||
| + | <tex>\Pi_0 = P</tex><br> | ||
| + | <tex>\Pi_1 = coNP</tex><br> | ||
| + | <tex>\Sigma_i \subset \Sigma_{i+1}</tex><br> | ||
| + | <tex>\Sigma_i \subset \Pi_{i+1}</tex> | ||
| + | |||
| + | <tex>\cup_{n=0}^{\infty} \Sigma_n = \cup_{n=0}^{\infty} \Pi_n = PH</tex> | ||
| + | |||
| + | ===Связь языков из <math>\Sigma_i</math> и <math>\Pi_i</math>=== | ||
| + | Если язык <tex>L</tex> принадлежит [[Классы Sigma_i|классу <math>\Sigma_i</math>]], то дополнение <tex>\overline{L}</tex> принадлежит [[Классы Sigma_i и Pi_i|классу <math>\Pi_i</math>]] | ||
| + | |||
| + | ==Коллапс полиномиальной иерархии== | ||
| + | Если <tex>\Sigma_n = \Sigma_{n+1}</tex> или <tex>\Sigma_n = \Pi_n</tex>, то по [[Теорема о коллапсе полиномиальной иерархии|теоремам о коллапсе полиномиальной иерархии]] полиномиальная иерархия сжимается до уровня <math>n</math>. То есть если <tex>i > n</tex>, то <tex>\Sigma_i = \Sigma_n</tex>. Это означает, что равенство классов [[Класс P|P]] и [[Класс NP|NP]] схлопывает полиномиальную иерархию. | ||
| + | |||
| + | ==Объединение классов полиномиальной иерархии== | ||
Объединение всех классов полиномиальной иерархии называется [[Класс PH|классом PH]]. | Объединение всех классов полиномиальной иерархии называется [[Класс PH|классом PH]]. | ||
Известно что [[Класс PH|PH]] является подмножеством [[Класс PS|PS]], но о равенстве между этими классами ничего не известно. | Известно что [[Класс PH|PH]] является подмножеством [[Класс PS|PS]], но о равенстве между этими классами ничего не известно. | ||
Текущая версия на 19:18, 4 сентября 2022
Полиномиальная иерархия - иерархия классов сложности, которая обобщает классы P, NP и coNP до вычислений с оракулом.
Содержание
Классы из полиномиальной иерархии
Приведем некоторые соотношения между классами и .
Связь языков из и
Если язык принадлежит классу , то дополнение принадлежит классу
Коллапс полиномиальной иерархии
Если или , то по теоремам о коллапсе полиномиальной иерархии полиномиальная иерархия сжимается до уровня . То есть если , то . Это означает, что равенство классов P и NP схлопывает полиномиальную иерархию.
Объединение классов полиномиальной иерархии
Объединение всех классов полиномиальной иерархии называется классом PH.
Известно что PH является подмножеством PS, но о равенстве между этими классами ничего не известно.