Очередь Майкла и Скотта — различия между версиями
(→Идея реализации) |
м (rollbackEdits.php mass rollback) |
||
| (не показано 14 промежуточных версий 6 участников) | |||
| Строка 1: | Строка 1: | ||
| − | '''Очередь Майкла и Скотта''' '' | + | '''Очередь Майкла и Скотта''' (англ. ''Michael-Scott Queue'') - алгоритм построения lock-free очереди. Впервые был предложен Maged M. Michael и Michael L. Scott <ref>[http://www.cs.rochester.edu/~scott/papers/1996_PODC_queues.pdf? Simple, Fast, and Practical Non-Blocking and BlockingConcurrent Queue Algorithms]</ref>. |
== Структура очереди == | == Структура очереди == | ||
Очередь построена на односвязном списке. Каждый элемент списка <tex>Node</tex> содержит ссылку на хранимые в нём данные и атомарный указатель на следующий элемент списка. | Очередь построена на односвязном списке. Каждый элемент списка <tex>Node</tex> содержит ссылку на хранимые в нём данные и атомарный указатель на следующий элемент списка. | ||
| − | ''' | + | '''class''' Node('''val''' data: '''Int''', '''val''' next: AtomicReference<Node>) |
| − | Если узел <tex>node</tex> является последним в списке, то <tex>node | + | Если узел <tex>node</tex> является последним в списке, то <tex>node.next</tex> указывает на <tex>null</tex>. |
| − | next</tex> указывает на <tex>null</tex>. | ||
| − | Сама очередь состоит из двух атомарных указателей: <tex>H</tex> на голову и<tex>T</tex> на хвост. Удаление из очереди происходит со стороны головы, добавление - со стороны хвоста. | + | Сама очередь состоит из двух атомарных указателей: <tex>H</tex> на голову и <tex>T</tex> на хвост. Удаление из очереди происходит со стороны головы, добавление - со стороны хвоста. |
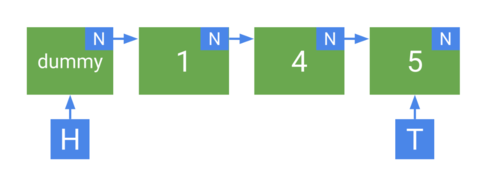
Голова списка является фиктивным элементом ''(dummy)''. Данные, хранимые в этом узле, не имеют значения. Изначально очередь состоит из одного ''dummy''-элемента, на который указывают <tex>T</tex> и <tex>H</tex>. | Голова списка является фиктивным элементом ''(dummy)''. Данные, хранимые в этом узле, не имеют значения. Изначально очередь состоит из одного ''dummy''-элемента, на который указывают <tex>T</tex> и <tex>H</tex>. | ||
| + | |||
| + | [[Файл:Структура_msqueue.PNG|500px|thumb|center|Структура очереди Майкла и Скотта]] | ||
'''class''' Queue | '''class''' Queue | ||
| Строка 18: | Строка 19: | ||
tail = '''new''' AtomicReference<Node>(dummy) | tail = '''new''' AtomicReference<Node>(dummy) | ||
| − | Будем поддерживать следующий инвариант: в нашей очереди <tex>H</tex> указывает на узел, находящийся не правее узла, на который указывает <tex>T</tex> | + | Будем поддерживать следующий инвариант: в нашей очереди <tex>H</tex> указывает на узел, находящийся не правее узла, на который указывает <tex>T</tex>. |
| − | == | + | ==Однопоточная реализация== |
=== Удаление элемента === | === Удаление элемента === | ||
| Строка 77: | Строка 78: | ||
При данной реализации мы сталкиваемся со следующей проблемой | При данной реализации мы сталкиваемся со следующей проблемой | ||
| − | == Описание проблемы == | + | === Описание проблемы === |
Рассмотрим ситуацию, при которой два потока <tex>A</tex> и <tex>B</tex> добавляют в очередь элементы <tex>elem</tex> и <tex>elem'</tex>. Рассмотрим следующую последовательность действий: | Рассмотрим ситуацию, при которой два потока <tex>A</tex> и <tex>B</tex> добавляют в очередь элементы <tex>elem</tex> и <tex>elem'</tex>. Рассмотрим следующую последовательность действий: | ||
| Строка 119: | Строка 120: | ||
'''CAS'''(T, tail, tail.next.get()) | '''CAS'''(T, tail, tail.next.get()) | ||
| − | == Проблема с <tex>pop</tex> == | + | == Корректная реализация <tex>pop</tex> == |
| + | |||
| + | === Проблема с <tex>pop</tex> === | ||
Если мы попытаемся воспользоваться написанной выше реализацией метода <tex>pop</tex>, инвариант очереди не будет соблюдён. В силу особенностей реализации метода <tex>push</tex>, в некоторые моменты <tex>T</tex> может указывать не на добавленный последним элемент, а на добавленный предпоследним. В таком случае, с помощью последовательности удалений можно добиться того, что <tex>H</tex> будет указывать на последний добавленный элемент, а <tex>T</tex> - на предпоследний. Таким образом, <tex>H</tex> будет указывать на вершину правее чем та, на которую указывает <tex>T</tex>, то есть инвариант очереди будет нарушен | Если мы попытаемся воспользоваться написанной выше реализацией метода <tex>pop</tex>, инвариант очереди не будет соблюдён. В силу особенностей реализации метода <tex>push</tex>, в некоторые моменты <tex>T</tex> может указывать не на добавленный последним элемент, а на добавленный предпоследним. В таком случае, с помощью последовательности удалений можно добиться того, что <tex>H</tex> будет указывать на последний добавленный элемент, а <tex>T</tex> - на предпоследний. Таким образом, <tex>H</tex> будет указывать на вершину правее чем та, на которую указывает <tex>T</tex>, то есть инвариант очереди будет нарушен | ||
| − | == Корректная реализация | + | === Корректная реализация === |
Основная проблема предыдущей реализации состоит в том, что в методе <tex>pop</tex> при перемещении <tex>H</tex>, мы никак не следили за положением <tex>T</tex>. Эту проблему можно исправить следующим образом: пусть в методе <tex>pop</tex> рабочий поток будет помогать переместить указатель <tex>T</tex> на последний добавленный элемент (аналогично действиям рабочего потока в методе <tex>push</tex>). | Основная проблема предыдущей реализации состоит в том, что в методе <tex>pop</tex> при перемещении <tex>H</tex>, мы никак не следили за положением <tex>T</tex>. Эту проблему можно исправить следующим образом: пусть в методе <tex>pop</tex> рабочий поток будет помогать переместить указатель <tex>T</tex> на последний добавленный элемент (аналогично действиям рабочего потока в методе <tex>push</tex>). | ||
| Строка 130: | Строка 133: | ||
'''def''' pop(): '''Int''' | '''def''' pop(): '''Int''' | ||
| − | |||
'''while''' ('''true'''): <font color=green>//CAS-цикл</font> | '''while''' ('''true'''): <font color=green>//CAS-цикл</font> | ||
head = H.get() <font color=green>//Сохраняем в локальные переменные текущие голову и хвост, а так же следующий за головным элемент</font> | head = H.get() <font color=green>//Сохраняем в локальные переменные текущие голову и хвост, а так же следующий за головным элемент</font> | ||
| Строка 149: | Строка 151: | ||
tail == head => tail.next == head.next | tail == head => tail.next == head.next | ||
*/</font> | */</font> | ||
| + | '''CAS'''(T, tail, nextHead) | ||
'''else''': | '''else''': | ||
<font color=green>// Очередь гарантированно не пуста, следующий элемент существует</font> | <font color=green>// Очередь гарантированно не пуста, следующий элемент существует</font> | ||
Текущая версия на 19:08, 4 сентября 2022
Очередь Майкла и Скотта (англ. Michael-Scott Queue) - алгоритм построения lock-free очереди. Впервые был предложен Maged M. Michael и Michael L. Scott [1].
Содержание
Структура очереди
Очередь построена на односвязном списке. Каждый элемент списка содержит ссылку на хранимые в нём данные и атомарный указатель на следующий элемент списка.
class Node(val data: Int, val next: AtomicReference<Node>)
Если узел является последним в списке, то указывает на .
Сама очередь состоит из двух атомарных указателей: на голову и на хвост. Удаление из очереди происходит со стороны головы, добавление - со стороны хвоста.
Голова списка является фиктивным элементом (dummy). Данные, хранимые в этом узле, не имеют значения. Изначально очередь состоит из одного dummy-элемента, на который указывают и .
class Queue
dummy = new Node(null, new AtomicReference<Node>(null))
head = new AtomicReference<Node>(dummy)
tail = new AtomicReference<Node>(dummy)
Будем поддерживать следующий инвариант: в нашей очереди указывает на узел, находящийся не правее узла, на который указывает .
Однопоточная реализация
Удаление элемента
Для удаления элемента необходимо переместить указатель на следующую в списке вершину.
def pop(): Int
if (H.next == null):
throw new EmptyException()
H = H.next
return H.data //H - новый фиктивный элемент
Добавление элемента
Создадим новый узел списка, и добавим его в конец очереди.
def push(x: Int):
newTail = new Node(x, new AtomicReference<Node>(null))
T.next = newTail //Добавление новой вершины в очередь
T = T.next //Изменение хвоста списка
Не lock-free многопоточная реализация
Будем при изменении , , и использовать .
Удаление элемента
Для удаления элемента необходимо переместить указатель на следующую в списке вершину.
def pop(): Int
while (true): //Поток пытается в CAS - цикле поменять указатель на H, пока не получится
head = H.get()
if (head.next == null):
throw new EmptyException()
newHead = head.next.get()
if (CAS(H, head, nextHead)):
return newHead.data
Добавление элемента
Создадим новый узел списка, и добавим его в конец очереди.
def push(x: Int):
newTail = new Node(x, new AtomicReference<Node>(null))
while (true): //Поток пытается в CAS - цикле поменять T.next, пока не получится
tail = T.get()
curTail = tail.next
if (CAS(curTail, null, newTail)): //Поток пытается добавить элемент в конец очереди
break
while (true): //Поток пытается в CAS - цикле поменять указатель на T, пока не получится
tail = T.get()
nextTail = tail.next.get()
if (CAS(T, tail, nextTail)):
break
При данной реализации мы сталкиваемся со следующей проблемой
Описание проблемы
Рассмотрим ситуацию, при которой два потока и добавляют в очередь элементы и . Рассмотрим следующую последовательность действий:
- Поток добавляет в очередь новую вершину, изменяя , но не успевает изменить так, чтобы он указывал на только что добавленную вершину.
- Планировщик операционной системы усыпляет поток .
- Поток собирается добавить новую вершину в очередь, но не может этого сделать, так как постоянно проваливает операцию (T.next не указывает на , так как поток на шаге добавил в очередь новую вершину, но не передвинул )
- Поток не сможет добавить в очередь новую вершину (а следовательно, завершить операцию ), до тех пор, пока планировщик операционной системы не разбудит поток , и поток не завершит добавление (то есть не передвинет на вершину, добавленную на шаге .)
Следовательно, у такой очереди нет гарантии прогресса, и этот алгоритм не lock-free.
Корректная lock-free реализация
Основная идея
Нельзя выполнить добавление элемента в очередь и перемещение атомарно. В таком случае, пусть остальные потоки помогают перенести указатель на хвост очереди. Если поток видит непустой (то есть если он провалил ), то он должен помочь перенести , то есть выполнить однократно. Если выполнен успешно, то хвост перемещён успешно (а значит, наш поток должен вернуться к добавлению нового элемента). Если же он выполнен неудачно, то это значит, что уже не указывает на , а значит, другой поток уже успешно переместил хвост (а значит, наш поток должен вернуться к добавлению нового элемента).
Реализация
def push(x: Int):
newTail = new Node(x, new AtomicReference<Node>(null))
while (true): //CAS-цикл
tail = T.get()
if (CAS(tail.next, null, newTail)):
/*
Если T указывает на последний добавленный элемент и
получилось добавить ещё один элемент в хвост,
пробуем передвинуть T. Если не получилось передвинуть T,
значит, другой поток сделал это за нас, завершаем работу.
Если получилось - то мы сами передвинули T, завершаем работу
*/
CAS(T, tail, newTail)
return
else:
/*
Если T - не последний добавленный элемент элемент, то передвигаем T на последний элемент
Если этого сделать не получилось, значит, это сделал другой поток.
Если получилось - значит, наш поток передвинул T на текущий последний элемент.
В любом случае, возвращаемся в начало CAS-цикла, чтобы завершить добавление в очередь новой вершины.
*/
CAS(T, tail, tail.next.get())
Корректная реализация
Проблема с
Если мы попытаемся воспользоваться написанной выше реализацией метода , инвариант очереди не будет соблюдён. В силу особенностей реализации метода , в некоторые моменты может указывать не на добавленный последним элемент, а на добавленный предпоследним. В таком случае, с помощью последовательности удалений можно добиться того, что будет указывать на последний добавленный элемент, а - на предпоследний. Таким образом, будет указывать на вершину правее чем та, на которую указывает , то есть инвариант очереди будет нарушен
Корректная реализация
Основная проблема предыдущей реализации состоит в том, что в методе при перемещении , мы никак не следили за положением . Эту проблему можно исправить следующим образом: пусть в методе рабочий поток будет помогать переместить указатель на последний добавленный элемент (аналогично действиям рабочего потока в методе ).
Для определения того, указывает ли на последний добавленный элемент, воспользуемся следующим соображением: если указывает на последний добавленный элемент, то , так как за последним добавленным элементом нет других элементов. В противном случае указывает на предпоследний добавленный элемент, и его надо передвинуть на последний добавленный.
def pop(): Int
while (true): //CAS-цикл
head = H.get() //Сохраняем в локальные переменные текущие голову и хвост, а так же следующий за головным элемент
tail = T.get()
nextHead = head.next.get()
if (head == tail):
/*
Если head и tail совпадают, это ещё не означает, что очередь пуста.
Возможно, что мы просто не успели подвинуть tail. Если tail.next не null,
то мы просто не успели подвинуть tail при добавлении.
*/
if (nextHead == null):
// Следующего элемента нет, очередь пуста
throw new EmptyException()
else:
/*
push не успел подвинуть T, наш поток должен помочь
tail == head => tail.next == head.next
*/
CAS(T, tail, nextHead)
else:
// Очередь гарантированно не пуста, следующий элемент существует
result = nextHead.data
if (CAS(H, head, nextHead)):
/*
Если получилось переставить голову, то фиктивным элементом стал
H.next, результат - данные, которые в нём лежали. Если не получилось -
возвращаемся в начало метода и пробуем ещё раз
*/
return result
Примечания
Источники информации
- Maurice Herliny & Nir Shavit - The Art of Multiprocessor programming, стр 230