Мультиплексор и демультиплексор — различия между версиями

Текущая версия на 19:11, 4 сентября 2022

Определение:

Мультиплексор (англ. multiplexer, или mux) — логическая схема, имеющая входов , , , , , , , и один выход , на который подаётся значение на входе , где — число, которое кодируется входами , , , .

Определение:

Демультиплексор (англ. demultiplexer, или demux) — логическая схема, имеющая входов , , , , и выходов , , , . На все выходы подаётся кроме выхода , на который подаётся значение на входе , где — число, которое кодируется входами , , , .

Содержание

1 Принцип работы мультиплексора
- 1.1 Мультиплексор 2-to-1
- 1.2 Мультиплексор 4-to-1
2 Логическая схема мультиплексора
3 Принцип работы демультиплексора
- 3.1 Демультиплексор 1-to-2
- 3.2 Демультиплексор 1-to-4
4 Логическая схема демультиплексора
5 Применение мультиплексора и демультиплексора в реальной жизни
6 См. также
7 Источники информации

Принцип работы мультиплексора

—to— мультиплексор

Мультиплексор 2-to-1

Рассмотрим мультиплексор [math]2[/math]-to-[math]1[/math] (это значит, что есть всего два входа [math]x_0[/math] и [math]x_1[/math], значения которых могут подаваться на вход [math]z[/math]). Переберём всевозможные варианты значений на входах. Если на [math]s[/math] подавать [math]0[/math], то на выход [math]z[/math] будет подаваться то же значение, которое подаётся на вход [math]x_0[/math], т.е. в данном случае значение на входе [math]x_1[/math] нас не интересует. Аналогично, если на вход [math]s[/math] подавать [math]1[/math], то на выход [math]z[/math] будет подаваться то же значение, которое подаётся на вход [math]x_1[/math].

[math]s[/math]	[math]x_0[/math]	[math]x_1[/math]	[math]z[/math]
[math]\textbf{0}[/math]	[math]\textbf{0}[/math]	[math]?[/math]	[math]\textbf{0}[/math]
[math]\textbf{0}[/math]	[math]\textbf{1}[/math]	[math]?[/math]	[math]\textbf{1}[/math]
[math]\textbf{1}[/math]	[math]?[/math]	[math]\textbf{0}[/math]	[math]\textbf{0}[/math]
[math]\textbf{1}[/math]	[math]?[/math]	[math]\textbf{1}[/math]	[math]\textbf{1}[/math]

Мультиплексор 4-to-1

Рассмотрим мультиплексор [math]4[/math]-to-[math]1[/math] (это значит, что есть четыре входа [math]x_0[/math], [math]x_1[/math], [math]x_2[/math] и [math]x_3[/math], значения которых могут подаваться на выход [math]z[/math]). Также переберём всевозможные варианты значений на входах. Тут уже [math]2[/math] входа [math]s_0[/math] и [math]s_1[/math], которые определяют, значение какого из входов [math]x_0[/math], [math]x_1[/math], [math]x_2[/math] или [math]x_3[/math] будет подаваться на выход [math]z[/math]. Если [math]s_0 = s_1 = 0[/math], то на выход [math]z[/math] будет подаваться значение входа [math]x_0[/math], если [math]s_0 = 1[/math] и [math]s_1 = 0[/math] — то значение [math]x_1[/math], если [math]s_0 = 0[/math] и [math]s_1 = 1[/math] — то значение [math]x_2[/math], в противном случае — значение [math]x_3[/math].

[math]s_0[/math]	[math]s_1[/math]	[math]x_0[/math]	[math]x_1[/math]	[math]x_2[/math]	[math]x_3[/math]	[math]z[/math]
[math]\textbf{0}[/math]	[math]\textbf{0}[/math]	[math]\textbf{0}[/math]	[math]?[/math]	[math]?[/math]	[math]?[/math]	[math]\textbf{0}[/math]
[math]\textbf{0}[/math]	[math]\textbf{0}[/math]	[math]\textbf{1}[/math]	[math]?[/math]	[math]?[/math]	[math]?[/math]	[math]\textbf{1}[/math]
[math]\textbf{1}[/math]	[math]\textbf{0}[/math]	[math]?[/math]	[math]\textbf{0}[/math]	[math]?[/math]	[math]?[/math]	[math]\textbf{0}[/math]
[math]\textbf{1}[/math]	[math]\textbf{0}[/math]	[math]?[/math]	[math]\textbf{1}[/math]	[math]?[/math]	[math]?[/math]	[math]\textbf{1}[/math]
[math]\textbf{0}[/math]	[math]\textbf{1}[/math]	[math]?[/math]	[math]?[/math]	[math]\textbf{0}[/math]	[math]?[/math]	[math]\textbf{0}[/math]
[math]\textbf{0}[/math]	[math]\textbf{1}[/math]	[math]?[/math]	[math]?[/math]	[math]\textbf{1}[/math]	[math]?[/math]	[math]\textbf{1}[/math]
[math]\textbf{1}[/math]	[math]\textbf{1}[/math]	[math]?[/math]	[math]?[/math]	[math]?[/math]	[math]\textbf{0}[/math]	[math]\textbf{0}[/math]
[math]\textbf{1}[/math]	[math]\textbf{1}[/math]	[math]?[/math]	[math]?[/math]	[math]?[/math]	[math]\textbf{1}[/math]	[math]\textbf{1}[/math]

Логическая схема мультиплексора

Основная статья: Шифратор и дешифратор

Заметим, что дешифратор имеет [math]n[/math] входов и [math]2^n[/math] выходов, причём на все выходы дешифратора подаётся [math]0[/math] кроме выхода [math]z_i[/math], на который подаётся [math]1[/math], где [math]i[/math] — число, которое кодируется его входами.

Тогда давайте построим дешифратор [math]n[/math]-to-[math]2^n[/math] (это значит, что у дешифратора имеется [math]n[/math] входов и [math]2^n[/math] выходов), на вход ему подадим значения входов [math]s_0[/math], [math]s_1[/math], [math]\ldots[/math], [math]s_{n-1}[/math], а выходы этого дешифратора обозначим как [math]y_0[/math], [math]y_1[/math], [math]\ldots[/math], [math]y_{2^n-1}[/math], а потом с помощью гейта [math]AND[/math] соединим выход [math]y_i[/math] дешифратора с входом [math]x_i[/math] мультиплексора, потом соединим все гейты с выходом [math]z[/math] с помощью гейта [math]OR[/math], у которого [math]2^n[/math] входов и один выход. Давайте разберёмся, почему эта схема правильная: очевидно, что если входы [math]s_0[/math], [math]s_1[/math], [math]\ldots[/math] [math]s_{n-1}[/math] кодируют вход [math]i[/math], то это значит, что только [math]y_i[/math] выход дешифратора будет иметь [math]1[/math], тогда как на остальных выходах будет [math]0[/math], значит, что значения на входах [math]x_0[/math], [math]x_1[/math], [math]\ldots[/math], [math]x_{i-1}[/math], [math]x_{i+1}[/math], [math]\ldots[/math], [math]x_{2^n-1}[/math] на ответ никак повлиять не могут. Теперь, если на входе [math]x_i[/math] было [math]0[/math], то на выходе [math]z[/math] будет [math]0[/math], если же на входе [math]x_i[/math] был [math]1[/math], то на выходе [math]z[/math] будет [math]1[/math].

Логическая схема мультиплексора -to-

Принцип работы демультиплексора

-to- демультиплексор

Демультиплексор 1-to-2

Рассмотрим демультиплексор [math]1[/math]-to-[math]2[/math] (это значит, что у демультиплексора два выхода). Если на вход [math]s[/math] подать значение [math]0[/math], то на выход [math]z_0[/math] будет подаваться то же значение, которое подаётся на вход [math]y[/math], а на выход [math]z_1[/math] будет подаваться [math]0[/math]. Если же на вход [math]s[/math] подать значение [math]1[/math], то на выход [math]z_0[/math] будет подаваться значение [math]0[/math], а на выход [math]z_1[/math] то же значение, которое будет подаваться на вход [math]y[/math].

[math]s[/math]	[math]y[/math]	[math]z_0[/math]	[math]z_1[/math]
[math]\textbf{0}[/math]	[math]\textbf{0}[/math]	[math]\textbf{0}[/math]	[math]0[/math]
[math]\textbf{0}[/math]	[math]\textbf{1}[/math]	[math]\textbf{1}[/math]	[math]0[/math]
[math]\textbf{1}[/math]	[math]\textbf{0}[/math]	[math]0[/math]	[math]\textbf{0}[/math]
[math]\textbf{1}[/math]	[math]\textbf{1}[/math]	[math]0[/math]	[math]\textbf{1}[/math]

Демультиплексор 1-to-4

Рассмотрим демультиплексор [math]1[/math]-to-[math]4[/math] (это значит, что у демультиплексора четыре выхода). Теперь у нас уже есть два входа [math]s_0[/math] и [math]s_1[/math], которые определяют, на какой из выходов [math]z_0[/math], [math]z_1[/math], [math]z_2[/math] или [math]z_3[/math] будет подаваться значение [math]y[/math], тогда как на остальные выходы будет подаваться [math]0[/math]. В случае, когда [math]s_0 = s_1 = 0[/math], то на выход [math]z_0[/math] будет подаваться значение на входе [math]y[/math], тогда как на [math]z_1[/math], [math]z_2[/math] и [math]z_3[/math] будет подаваться [math]0[/math]. Если же [math]s_0 = 1[/math] и [math]s_1 = 0[/math], то на выходы [math]z_0[/math], [math]z_2[/math] и [math]z_3[/math] будет подаваться [math]0[/math], а на выход [math]z_1[/math] будет подаваться то же, что подаётся на вход [math]y[/math]. Аналогично разбираются случаи [math]s_0 = 0[/math], [math]s_1 = 1[/math] и [math]s_0 = s_1 = 1[/math].

[math]s_0[/math]	[math]s_1[/math]	[math]y[/math]	[math]z_0[/math]	[math]z_1[/math]	[math]z_2[/math]	[math]z_3[/math]
[math]\textbf{0}[/math]	[math]\textbf{0}[/math]	[math]\textbf{0}[/math]	[math]\textbf{0}[/math]	[math]0[/math]	[math]0[/math]	[math]0[/math]
[math]\textbf{0}[/math]	[math]\textbf{0}[/math]	[math]\textbf{1}[/math]	[math]\textbf{1}[/math]	[math]0[/math]	[math]0[/math]	[math]0[/math]
[math]\textbf{1}[/math]	[math]\textbf{0}[/math]	[math]\textbf{0}[/math]	[math]0[/math]	[math]\textbf{0}[/math]	[math]0[/math]	[math]0[/math]
[math]\textbf{1}[/math]	[math]\textbf{0}[/math]	[math]\textbf{1}[/math]	[math]0[/math]	[math]\textbf{1}[/math]	[math]0[/math]	[math]0[/math]
[math]\textbf{0}[/math]	[math]\textbf{1}[/math]	[math]\textbf{0}[/math]	[math]0[/math]	[math]0[/math]	[math]\textbf{0}[/math]	[math]0[/math]
[math]\textbf{0}[/math]	[math]\textbf{1}[/math]	[math]\textbf{1}[/math]	[math]0[/math]	[math]0[/math]	[math]\textbf{1}[/math]	[math]0[/math]
[math]\textbf{1}[/math]	[math]\textbf{1}[/math]	[math]\textbf{0}[/math]	[math]0[/math]	[math]0[/math]	[math]0[/math]	[math]\textbf{0}[/math]
[math]\textbf{1}[/math]	[math]\textbf{1}[/math]	[math]\textbf{1}[/math]	[math]0[/math]	[math]0[/math]	[math]0[/math]	[math]\textbf{1}[/math]

Логическая схема демультиплексора

Построим схему, аналогичную схеме мультиплексора.

Тогда давайте построим дешифратор, [math]n[/math]-to-[math]2^n[/math], на входы дешифратора подадим входы [math]s_0[/math], [math]s_1[/math], [math]\ldots[/math], [math]s_{n-1}[/math], а выходы этого дешифратора мы обозначим как [math]y_0[/math], [math]y_1[/math], [math]\ldots[/math], [math]y_{2^n-1}[/math]. Поставим [math]2^n[/math] гейтов [math]AND[/math] и соединим каждый из выходов дешифратора [math]y_0[/math], [math]y_1[/math], [math]\ldots[/math], [math]y_{2^n-1}[/math] со входом [math]x[/math] с помощью гейта [math]AND[/math], потом соединим соответственные гейты с выходами [math]z_0[/math], [math]z_1[/math], [math]\ldots[/math], [math]z_{2^n-1}[/math], причем мы соединим гейт [math]AND[/math] с выходом [math]z_i[/math], если на этот гейт приходится выход дешифратора [math]y_i[/math].

Логическая схема демультиплексора -to-

Применение мультиплексора и демультиплексора в реальной жизни

Мультиплексоры и демультиплексоры часто используются в электронных схемах.

В качестве примера можно рассмотреть использование мультиплексоров для разделения на временные слоты и предоставления каждому объекту логической цепи своего слота, во время которого можно обмениваться данными с другими объектами. Данный способ позволяет использовать как можно меньше проводов для соединения объектов между собою. Такой принцип применяется при построении телефонных станций, которые соединяются с помощью одного провода, а для обеспечения помехоустойчивой связи используются временные слоты, в которые только одна из станций может обмениваться данными с остальными.

Также мультиплексоры и демультиплексоры используются в современных телефонах для преобразование сигналов в голосовые сообщения, поскольку позволяют с помощью малого (порядка [math]30[/math] входов) воспроизводить любой сигнал с частотой, которую может различить человеческое ухо.

Кроме того, мультиплексоры используются и при производстве компьютерных компонентов.

См. также

Источники информации

@@ Строка 1: / Строка 1: @@
-<div style="background-color: #ABCDEF; font-size: 16px; font-weight: bold; color: #000000; text-align: center; padding: 4px; border-style: solid; border-width: 1px;">Эта статья находится в разработке!</div>
-<includeonly>[[Категория: В разработке]]</includeonly>
 {{Определение
-|definition='''Мультиплексор''' (англ. ''multiplexer'', или ''mux'') - логический элемент, имеющий $2^n + n$ входов $x_0$, $x_1$, $\ldots$, $x_{2^n-1}$, $s_0$, $s_1$, $\ldots$, $s_{n-1}$ и один выход $z$, на который подаётся значение на входе $x_i$, где $i$ - число, которое кодируется входами $s_0$, $s_1$, $\ldots$, $s_{n-1}$.
+|definition='''Мультиплексор''' (англ. ''multiplexer'', или ''mux'') — [[Реализация булевой функции схемой из функциональных элементов|логическая схема]], имеющая <tex>2^n + n</tex> входов <tex>x_0</tex>, <tex>x_1</tex>, <tex>\ldots</tex>, <tex>x_{2^n-1}</tex>, <tex>s_0</tex>, <tex>s_1</tex>, <tex>\ldots</tex>, <tex>s_{n-1}</tex> и один выход <tex>z</tex>, на который подаётся значение на входе <tex>x_i</tex>, где <tex>i</tex> — число, которое кодируется входами <tex>s_0</tex>, <tex>s_1</tex>, <tex>\ldots</tex>, <tex>s_{n-1}</tex>.
 }}
 {{Определение
-|definition='''Демультиплексор''' (англ. ''demultiplexer'', или ''demux'') - логический элемент, имеющий $n+1$ входов $s_0$, $s_1$, $\ldots$, $s_{n-1}$, $x$ и $2^n$ выходов $z_0$, $z_1$, $\ldots$, $z_{2^n-1}$. На все выходы подаётся $0$ кроме выхода $z_i$, на который подаётся значение на входе $y$, где $i$ - число, которое кодируется входами $s_0$, $s_1$, $\ldots$, $s_{n-1}$.
+|definition='''Демультиплексор''' (англ. ''demultiplexer'', или ''demux'') — логическая схема, имеющая <tex>n+1</tex> входов <tex>s_0</tex>, <tex>s_1</tex>, <tex>\ldots</tex>, <tex>s_{n-1}</tex>, <tex>y</tex> и <tex>2^n</tex> выходов <tex>z_0</tex>, <tex>z_1</tex>, <tex>\ldots</tex>, <tex>z_{2^n-1}</tex>. На все выходы подаётся <tex>0</tex> кроме выхода <tex>z_i</tex>, на который подаётся значение на входе <tex>y</tex>, где <tex>i</tex> — число, которое кодируется входами <tex>s_0</tex>, <tex>s_1</tex>, <tex>\ldots</tex>, <tex>s_{n-1}</tex>.
 }}
 ==Принцип работы мультиплексора==
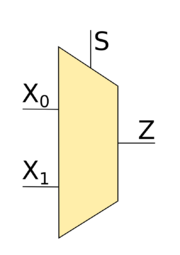
-[[Файл:2to1mux.png|thumb|180px|2-to-1 мультиплексор]]
+[[Файл:2to1mux.png|thumb|180px|<tex>2</tex>—to—<tex>1</tex> мультиплексор]]
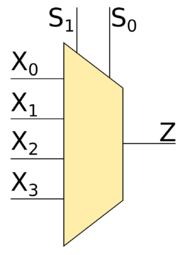
-[[Файл:4to1mux.png|thumb|180px|4-to-1 мультиплексор]]
+[[Файл:4to1mux.png|thumb|180px|<tex>4</tex>—to—<tex>1</tex> мультиплексор]]
 ===Мультиплексор 2-to-1===
-Рассмотрим мультиплексор $2-to-1$ (это значит, что есть всего два входа $x_0$ и $x_1$, значения которых могут подаваться на вход $z$). Переберём всевозможные варианты значений на входах. Если на $s$ подавать $0$, то на выход $z$ будет подаваться то же значение, которое подаётся на вход $x_0$, т.е. в данном случае значение на входе $x_1$ нас не интересует. Аналогично, если на вход $s$ подавать $1$, то на выход $z$ будет подаваться то же значение, которое подаётся на вход $x_1$. Для более лучшего понимания посмотрим на таблицу истинности.
+Рассмотрим мультиплексор <tex>2</tex>-to-<tex>1</tex> (это значит, что есть всего два входа <tex>x_0</tex> и <tex>x_1</tex>, значения которых могут подаваться на вход <tex>z</tex>). Переберём всевозможные варианты значений на входах. Если на <tex>s</tex> подавать <tex>0</tex>, то на выход <tex>z</tex> будет подаваться то же значение, которое подаётся на вход <tex>x_0</tex>, т.е. в данном случае значение на входе <tex>x_1</tex> нас не интересует. Аналогично, если на вход <tex>s</tex> подавать <tex>1</tex>, то на выход <tex>z</tex> будет подаваться то же значение, которое подаётся на вход <tex>x_1</tex>.
 {| class="wikitable"
-|-
+|-style="text-align:center;"
-! $s$ !! $x_0$ !! $x_1$ !! $z$
+! <tex>s</tex> !! <tex>x_0</tex> !! <tex>x_1</tex> !! <tex>z</tex>
-|-
+|-style="text-align:center;"
-| '''0''' || '''0''' || ? || '''0'''
+| <tex>\textbf{0}</tex> || <tex>\textbf{0}</tex> || <tex>?</tex> || <tex>\textbf{0}</tex>
-|-
+|-style="text-align:center;"
-| '''0''' || '''1''' || ? || '''1'''
+| <tex>\textbf{0}</tex> || <tex>\textbf{1}</tex> || <tex>?</tex> || <tex>\textbf{1}</tex>
-|-
+|-style="text-align:center;"
-| '''1''' || ? || '''0''' || '''0'''
+| <tex>\textbf{1}</tex> || <tex>?</tex> || <tex>\textbf{0}</tex> || <tex>\textbf{0}</tex>
-|-
+|-style="text-align:center;"
-| '''1''' || ? || '''1''' || '''1'''
+| <tex>\textbf{1}</tex> || <tex>?</tex> || <tex>\textbf{1}</tex> || <tex>\textbf{1}</tex>
 |}
 ===Мультиплексор 4-to-1===
-Также рассмотрим мультиплексор $4-to-1$ (это значит, что есть четыре входа $x_0$, $x_1$, $x_2$ и $x_3$, значения которых могут подаваться на выход $z$). Также переберём всевозможные варианты значений на входах. Тут уже 2 входа $s_0$ и $s_1$, которые определяют, значение какого из входов $x_0$, $x_1$, $x_2$ или $x_3$ будет подаваться на выход $z$. Если $s_0 = s_1 = 0$, то на выход $z$ будет подаваться значение входа $x_0$, если $s_0 = 1$ и $s_1 = 0$ $-$ то значение $x_1$, если $s_0 = 0$ и $s_1 = 1$ $-$ то значение $x_2$, в противном случае $-$ значение $x_3$. Для более лучшее понимания рекомендуется обратиться к таблице истинности.
+Рассмотрим мультиплексор <tex>4</tex>-to-<tex>1</tex> (это значит, что есть четыре входа <tex>x_0</tex>, <tex>x_1</tex>, <tex>x_2</tex> и <tex>x_3</tex>, значения которых могут подаваться на выход <tex>z</tex>). Также переберём всевозможные варианты значений на входах. Тут уже <tex>2</tex> входа <tex>s_0</tex> и <tex>s_1</tex>, которые определяют, значение какого из входов <tex>x_0</tex>, <tex>x_1</tex>, <tex>x_2</tex> или <tex>x_3</tex> будет подаваться на выход <tex>z</tex>. Если <tex>s_0 = s_1 = 0</tex>, то на выход <tex>z</tex> будет подаваться значение входа <tex>x_0</tex>, если <tex>s_0 = 1</tex> и <tex>s_1 = 0</tex> — то значение <tex>x_1</tex>, если <tex>s_0 = 0</tex> и <tex>s_1 = 1</tex> — то значение <tex>x_2</tex>, в противном случае — значение <tex>x_3</tex>.
-{| class="wikitable"
-|-
+{| class="wikitable" align="center"
-! $s_0$ !! $s_1$ !! $x_0$ !! $x_1$ !! $x_2$ !! $x_3$ !! $z$
+|- align="center"
-|-
+! <tex>s_0</tex> !! <tex>s_1</tex> !! <tex>x_0</tex> !! <tex>x_1</tex> !! <tex>x_2</tex> !! <tex>x_3</tex> !! <tex>z</tex>
-| '''0''' || '''0''' || '''0''' || ? || ? || ? || '''0'''
+|- align="center"
-|-
+| <tex>\textbf{0}</tex> || <tex>\textbf{0}</tex> || <tex>\textbf{0}</tex> || <tex>?</tex> || <tex>?</tex> || <tex>?</tex> || <tex>\textbf{0}</tex>
-| '''0''' || '''0''' || '''1''' || ? || ? || ? || '''1'''
+|- align="center"
-|-
+| <tex>\textbf{0}</tex> || <tex>\textbf{0}</tex> || <tex>\textbf{1}</tex> || <tex>?</tex> || <tex>?</tex> || <tex>?</tex> || <tex>\textbf{1}</tex>
-| '''1''' || '''0''' || ? || '''0''' || ? || ? || '''0'''
+|- align="center"
-|-
+| <tex>\textbf{1}</tex> || <tex>\textbf{0}</tex> || <tex>?</tex> || <tex>\textbf{0}</tex> || <tex>?</tex> || <tex>?</tex> || <tex>\textbf{0}</tex>
-| '''1''' || '''0''' || ? || '''1''' || ? || ? || '''1'''
+|- align="center"
-|-
+| <tex>\textbf{1}</tex> || <tex>\textbf{0}</tex> || <tex>?</tex> || <tex>\textbf{1}</tex> || <tex>?</tex> || <tex>?</tex> || <tex>\textbf{1}</tex>
-| '''0''' || '''1''' || ? || ? || '''0''' || ? || '''0'''
+|- align="center"
-|-
+| <tex>\textbf{0}</tex> || <tex>\textbf{1}</tex> || <tex>?</tex> || <tex>?</tex> || <tex>\textbf{0}</tex> || <tex>?</tex> || <tex>\textbf{0}</tex>
-| '''0''' || '''1''' || ? || ? || '''1''' || ? || '''1'''
+|- align="center"
-|-
+| <tex>\textbf{0}</tex> || <tex>\textbf{1}</tex> || <tex>?</tex> || <tex>?</tex> || <tex>\textbf{1}</tex> || <tex>?</tex> || <tex>\textbf{1}</tex>
-| '''1''' || '''1''' || ? || ? || ? || '''0''' || '''0'''
+|- align="center"
-|-
+| <tex>\textbf{1}</tex> || <tex>\textbf{1}</tex> || <tex>?</tex> || <tex>?</tex> || <tex>?</tex> || <tex>\textbf{0}</tex> || <tex>\textbf{0}</tex>
-| '''1''' || '''1''' || ? || ? || ? || '''1''' || '''1'''
+|- align="center"
+| <tex>\textbf{1}</tex> || <tex>\textbf{1}</tex> || <tex>?</tex> || <tex>?</tex> || <tex>?</tex> || <tex>\textbf{1}</tex> || <tex>\textbf{1}</tex>
 |}
 ==Логическая схема мультиплексора==
-[[Файл:LogicSircuit1to8.png|thumb|180px|Логическая схема мультиплексора 8-to-1]]
+{{main|Шифратор и дешифратор}}
-Заметим, что [[дешифратор]] имеет $n$ входов и $2^n$ выходов, причём на все выходы дешифратора подаётся $0$ кроме выхода $z_i$, на который подаётся $1$, где $i$ - число, которое кодируется его входами.
+Заметим, что дешифратор имеет <tex>n</tex> входов и <tex>2^n</tex> выходов, причём на все выходы дешифратора подаётся <tex>0</tex> кроме выхода <tex>z_i</tex>, на который подаётся <tex>1</tex>, где <tex>i</tex> — число, которое кодируется его входами.
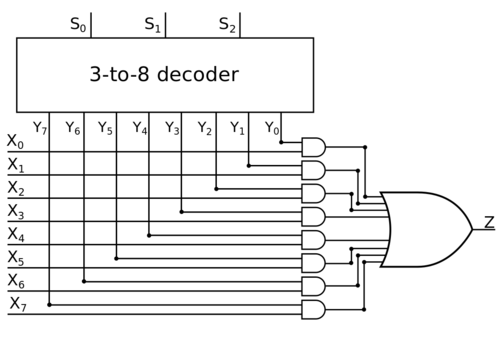
-Тогда давайте построим дешифратор ${n}-to-{2^n}$ (это значит, что у дешифратора имеется $n$ входов и $2^n$ выходов), на вход ему подадим входы $s_0$, $s_1$, $\ldots$, $s_{n-1}$, а выходы этого дешифратора обозначим как $y_0$, $y_1$, $\ldots$, $y_{2^n-1}$,  а потом с помощью гейта $AND$ соединим выход $y_i$ дешифратора с входом $x_i$ мультиплексора, потом соединим все гейты с выходом $z$. Давайте разберёмся, почему эта схема правильная: очевидно, что если входы $s_0$, $s_1$, $\ldots$ $s_{n-1}$ кодируют вход $i$, то это значит, что только $y_i$ выход дешифратора будет иметь $1$, тогда как на остальных выходах будет $0$, значит, что значения на входах $x_0$, $x_1$, $\ldots$, $x_{i-1}$, $x_{i+1}$, $\ldots$, $x_{2^n-1}$ на ответ никак повлиять не могут. Теперь, если на входе $x_i$ было $0$, то на выходе $z$ будет $0$, если же на входе $x_i$ был $1$, то на выходе $z$ будет $1$.
+Тогда давайте построим дешифратор <tex>n</tex>-to-<tex>2^n</tex> (это значит, что у дешифратора имеется <tex>n</tex> входов и <tex>2^n</tex> выходов), на вход ему подадим значения входов <tex>s_0</tex>, <tex>s_1</tex>, <tex>\ldots</tex>, <tex>s_{n-1}</tex>, а выходы этого дешифратора обозначим как <tex>y_0</tex>, <tex>y_1</tex>, <tex>\ldots</tex>, <tex>y_{2^n-1}</tex>,  а потом с помощью гейта <tex>AND</tex> соединим выход <tex>y_i</tex> дешифратора с входом <tex>x_i</tex> мультиплексора, потом соединим все гейты с выходом <tex>z</tex> с помощью гейта <tex>OR</tex>, у которого <tex>2^n</tex> входов и один выход. Давайте разберёмся, почему эта схема правильная: очевидно, что если входы <tex>s_0</tex>, <tex>s_1</tex>, <tex>\ldots</tex> <tex>s_{n-1}</tex> кодируют вход <tex>i</tex>, то это значит, что только <tex>y_i</tex> выход дешифратора будет иметь <tex>1</tex>, тогда как на остальных выходах будет <tex>0</tex>, значит, что значения на входах <tex>x_0</tex>, <tex>x_1</tex>, <tex>\ldots</tex>, <tex>x_{i-1}</tex>, <tex>x_{i+1}</tex>, <tex>\ldots</tex>, <tex>x_{2^n-1}</tex> на ответ никак повлиять не могут. Теперь, если на входе <tex>x_i</tex> было <tex>0</tex>, то на выходе <tex>z</tex> будет <tex>0</tex>, если же на входе <tex>x_i</tex> был <tex>1</tex>, то на выходе <tex>z</tex> будет <tex>1</tex>.
+{|
+|[[Файл:LogicSircuit1to8.png|thumb|500px|Логическая схема мультиплексора <tex>8</tex>-to-<tex>1</tex>]]
+|}
 ==Принцип работы демультиплексора==
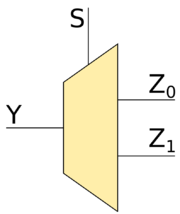
-[[Файл:1to2demux.png|thumb|180px|1-to-2 демультиплексор]]
+[[Файл:1to2demux.png|thumb|180px|<tex>1</tex>-to-<tex>2</tex> демультиплексор]]
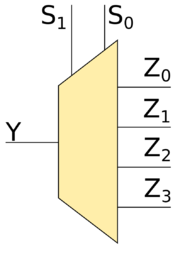
-[[Файл:1to4demux.png|thumb|180px|1-to-4 демультиплексор]]
+[[Файл:1to4demux.png|thumb|180px|<tex>1</tex>-to-<tex>4</tex> демультиплексор]]
 ===Демультиплексор 1-to-2===
-Рассмотрим демультиплексор $1-to-2$ (это значит, что у демультиплексора два выхода). Если на вход $s$ подать значение $0$, то на выход $z_0$ будет подаваться то же значение, которое подаётся на вход $y$, а на выход $z_1$ будет подаваться $0$. Если же на вход $s$ подать значение $1$, то на выход $z_0$ будет подаваться значение $0$, а на выход $z_1$ то же значение, которое будет подаваться на вход $y$. Для более лучшего понимания посмотрим на таблицу истинности.
+Рассмотрим демультиплексор <tex>1</tex>-to-<tex>2</tex> (это значит, что у демультиплексора два выхода). Если на вход <tex>s</tex> подать значение <tex>0</tex>, то на выход <tex>z_0</tex> будет подаваться то же значение, которое подаётся на вход <tex>y</tex>, а на выход <tex>z_1</tex> будет подаваться <tex>0</tex>. Если же на вход <tex>s</tex> подать значение <tex>1</tex>, то на выход <tex>z_0</tex> будет подаваться значение <tex>0</tex>, а на выход <tex>z_1</tex> то же значение, которое будет подаваться на вход <tex>y</tex>.
 {| class="wikitable"
-|-
+|- align="center"
-! $s$ !! $y$ !! $z_0$ !! $z_1$
+! <tex>s</tex> !! <tex>y</tex> !! <tex>z_0</tex> !! <tex>z_1</tex>
-|-
+|- align="center"
-| '''0''' || '''0''' || '''0''' || 0
+| <tex>\textbf{0}</tex> || <tex>\textbf{0}</tex> || <tex>\textbf{0}</tex> || <tex>0</tex>
-|-
+|- align="center"
-| '''0''' || '''1''' || '''1''' || 0
+| <tex>\textbf{0}</tex> || <tex>\textbf{1}</tex> || <tex>\textbf{1}</tex> || <tex>0</tex>
-|-
+|- align="center"
-| '''1''' || '''0''' || 0 || '''0'''
+| <tex>\textbf{1}</tex> || <tex>\textbf{0}</tex> || <tex>0</tex> || <tex>\textbf{0}</tex>
-|-
+|- align="center"
-| '''1''' || '''1''' || 0 || '''1'''
+| <tex>\textbf{1}</tex> || <tex>\textbf{1}</tex> || <tex>0</tex> || <tex>\textbf{1}</tex>
 |}
 ===Демультиплексор 1-to-4===
-Также рассмотрим демультиплексор $1-to-4$ (это значит, что у демультиплексора четыре выхода). Теперь у нас уже есть два входа $s_0$ и $s_1$, которые определяют, на какой из выходов $z_0$, $z_1$, $z_2$ или $z_3$ будет подаваться значение $y$, тогда как на остальные выходы будет подаваться $0$. В случае, когда $s_0 = s_1 = 0$, то на выход $z_0$ будет подаваться значение на входе $y$, тогда как на $z_1$, $z_2$ и $z_3$ будет подаваться $0$. Если же $s_0 = 1$ и $s_1 = 0$, то на выходы $z_0$, $z_2$ и $z_3$ будет подаваться $0$, а на выход $z_1$ будет подаваться то же, что подаётся на вход $y$. Аналогично разбираются случаи $s_0 = 0$, $s_1 = 1$ и $s_0 = s_1 = 1$. Для более лучшего понимания посмотрим на таблицу истинности.
+Рассмотрим демультиплексор <tex>1</tex>-to-<tex>4</tex> (это значит, что у демультиплексора четыре выхода). Теперь у нас уже есть два входа <tex>s_0</tex> и <tex>s_1</tex>, которые определяют, на какой из выходов <tex>z_0</tex>, <tex>z_1</tex>, <tex>z_2</tex> или <tex>z_3</tex> будет подаваться значение <tex>y</tex>, тогда как на остальные выходы будет подаваться <tex>0</tex>. В случае, когда <tex>s_0 = s_1 = 0</tex>, то на выход <tex>z_0</tex> будет подаваться значение на входе <tex>y</tex>, тогда как на <tex>z_1</tex>, <tex>z_2</tex> и <tex>z_3</tex> будет подаваться <tex>0</tex>. Если же <tex>s_0 = 1</tex> и <tex>s_1 = 0</tex>, то на выходы <tex>z_0</tex>, <tex>z_2</tex> и <tex>z_3</tex> будет подаваться <tex>0</tex>, а на выход <tex>z_1</tex> будет подаваться то же, что подаётся на вход <tex>y</tex>. Аналогично разбираются случаи <tex>s_0 = 0</tex>, <tex>s_1 = 1</tex> и <tex>s_0 = s_1 = 1</tex>.
 {| class="wikitable"
-|-
+|- align="center"
-! $s_0$ !! $s_1$ !! $y$ !! $z_0$ !! $z_1$ !! $z_2$ !! $z_3$
+! <tex>s_0</tex> !! <tex>s_1</tex> !! <tex>y</tex> !! <tex>z_0</tex> !! <tex>z_1</tex> !! <tex>z_2</tex> !! <tex>z_3</tex>
-|-
+|- align="center"
-| '''0''' || '''0''' || '''0''' || '''0''' || 0 || 0 || 0
+| <tex>\textbf{0}</tex> || <tex>\textbf{0}</tex> || <tex>\textbf{0}</tex> || <tex>\textbf{0}</tex> || <tex>0</tex> || <tex>0</tex> || <tex>0</tex>
-|-
+|- align="center"
-| '''0''' || '''0''' || '''1''' || '''1''' || 0 || 0 || 0
+| <tex>\textbf{0}</tex> || <tex>\textbf{0}</tex> || <tex>\textbf{1}</tex> || <tex>\textbf{1}</tex> || <tex>0</tex> || <tex>0</tex> || <tex>0</tex>
-|-
+|- align="center"
-| '''1''' || '''0''' || '''0''' || 0 || '''0''' || 0 || 0
+| <tex>\textbf{1}</tex> || <tex>\textbf{0}</tex> || <tex>\textbf{0}</tex> || <tex>0</tex> || <tex>\textbf{0}</tex> || <tex>0</tex> || <tex>0</tex>
-|-
+|- align="center"
-| '''1''' || '''0''' || '''1''' || 0 || '''1''' || 0 || 0
+| <tex>\textbf{1}</tex> || <tex>\textbf{0}</tex> || <tex>\textbf{1}</tex> || <tex>0</tex> || <tex>\textbf{1}</tex> || <tex>0</tex> || <tex>0</tex>
-|-
+|- align="center"
-| '''0''' || '''1''' || '''0''' || 0 || 0 || '''0''' || 0
+| <tex>\textbf{0}</tex> || <tex>\textbf{1}</tex> || <tex>\textbf{0}</tex> || <tex>0</tex> || <tex>0</tex> || <tex>\textbf{0}</tex> || <tex>0</tex>
-|-
+|- align="center"
-| '''0''' || '''1''' || '''1''' || 0 || 0 || '''1''' || 0
+| <tex>\textbf{0}</tex> || <tex>\textbf{1}</tex> || <tex>\textbf{1}</tex> || <tex>0</tex> || <tex>0</tex> || <tex>\textbf{1}</tex> || <tex>0</tex>
-|-
+|- align="center"
-| '''1''' || '''1''' || '''0''' || 0 || 0 || 0 || '''0'''
+| <tex>\textbf{1}</tex> || <tex>\textbf{1}</tex> || <tex>\textbf{0}</tex> || <tex>0</tex> || <tex>0</tex> || <tex>0</tex> || <tex>\textbf{0}</tex>
-|-
+|- align="center"
-| '''1''' || '''1''' || '''1''' || 0 || 0 || 0 || '''1'''
+| <tex>\textbf{1}</tex> || <tex>\textbf{1}</tex> || <tex>\textbf{1}</tex> || <tex>0</tex> || <tex>0</tex> || <tex>0</tex> || <tex>\textbf{1}</tex>
 |}
 ==Логическая схема демультиплексора==
-[[Файл:LogicSircuit1to8demux.png|thumb|180px|Логическая схема демультиплексора 1-to-8]]
+Построим схему, аналогичную схеме мультиплексора.
+Тогда давайте построим дешифратор, <tex>n</tex>-to-<tex>2^n</tex>, на входы дешифратора подадим входы <tex>s_0</tex>, <tex>s_1</tex>, <tex>\ldots</tex>, <tex>s_{n-1}</tex>,  а выходы этого дешифратора мы обозначим как <tex>y_0</tex>, <tex>y_1</tex>, <tex>\ldots</tex>, <tex>y_{2^n-1}</tex>. Поставим <tex>2^n</tex> гейтов <tex>AND</tex> и соединим каждый из выходов дешифратора <tex>y_0</tex>, <tex>y_1</tex>, <tex>\ldots</tex>, <tex>y_{2^n-1}</tex> со входом <tex>x</tex> с помощью гейта <tex>AND</tex>, потом соединим соответственные гейты с выходами <tex>z_0</tex>, <tex>z_1</tex>, <tex>\ldots</tex>, <tex>z_{2^n-1}</tex>, причем мы соединим гейт <tex>AND</tex> с выходом <tex>z_i</tex>, если на этот гейт приходится выход дешифратора <tex>y_i</tex>.
+{|
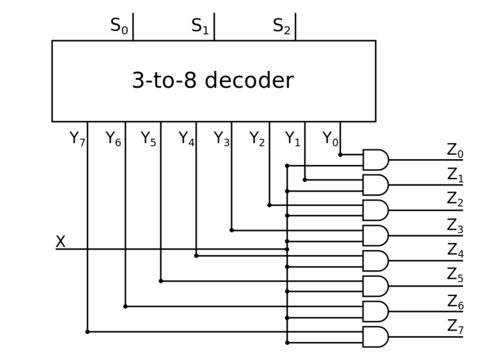
+|[[Файл:LogicSircuit1to8demux.png|thumb|500px|Логическая схема демультиплексора <tex>1</tex>-to-<tex>8</tex>]]
+|}
+==Применение мультиплексора и демультиплексора в реальной жизни==
-Построим схему, аналогичную схеме мультиплексора.
+Мультиплексоры и демультиплексоры часто используются в электронных схемах.
+В качестве примера можно рассмотреть использование мультиплексоров для разделения на временные слоты и предоставления каждому объекту логической цепи своего слота, во время которого можно обмениваться данными с другими объектами. Данный способ позволяет использовать как можно меньше проводов для соединения объектов между собою. Такой принцип применяется при построении телефонных станций, которые соединяются с помощью одного провода, а для обеспечения помехоустойчивой связи используются временные слоты, в которые только одна из станций может обмениваться данными с остальными.
+Также мультиплексоры и демультиплексоры используются в современных телефонах для преобразование сигналов в голосовые сообщения, поскольку позволяют с помощью малого (порядка <tex>30</tex> входов) воспроизводить любой сигнал с частотой, которую может различить человеческое ухо.
-Тогда давайте построим дешифратор, ${n}-to-{2^n}$, на входы дешифратора подадим входы $s_0$, $s_1$, $\ldots$, $s_{n-1}$,  а выходы этого дешифратора мы обозначим как $y_0$, $y_1$, $\ldots$, $y_{2^n-1}$. Поставим $2^n$ гейтов $AND$ и соединим каждый из выходов дешифратора $y_0$, $y_1$, $\ldots$, $y_{2^n-1}$ со входом $x$ с помощью гейта $AND$, потом соединим соответственные гейты с выходами $z_0$, $z_1$, $\ldots$, $z_{2^n-1}$, причем мы соединим гейт $AND$ с выходом $z_i$, если на этот гейт приходится выход дешифратора $y_i$.
+Кроме того, мультиплексоры используются и при производстве компьютерных компонентов.
 ==См. также==
+*[[Реализация булевой функции схемой из функциональных элементов]]
 *[[Метод Лупанова синтеза схем]]
-*[[Дешифратор]]
+*[[Шифратор и дешифратор]]
 ==Источники информации==
 *[https://en.wikipedia.org/wiki/Multiplexer Wikipedia - Multiplexer]
+*[https://books.google.ru/books?id=UD0h_GqgbHgC&printsec=frontcover&dq=network%2B+guide+to+networks&redir_esc=y#v=onepage&q&f=false Dean, Tamara (2010), Network+ Guide to Networks, стр. 79-84]
 [[Категория: Дискретная математика и алгоритмы]]
-[[Категория: Схемы из функциональных элементов ]]
+[[Категория: Схемы из функциональных элементов]]

Мультиплексор и демультиплексор — различия между версиями

Текущая версия на 19:11, 4 сентября 2022

Содержание

Принцип работы мультиплексора

Мультиплексор 2-to-1

Мультиплексор 4-to-1

Логическая схема мультиплексора

Принцип работы демультиплексора

Демультиплексор 1-to-2

Демультиплексор 1-to-4

Логическая схема демультиплексора

Применение мультиплексора и демультиплексора в реальной жизни

См. также

Источники информации

Навигация

Персональные инструменты

Пространства имён

Варианты

Просмотры

Ещё

Поиск

Навигация

Инструменты