Метод опорных векторов (SVM) — различия между версиями
Egormkn (обсуждение | вклад) м |
м (rollbackEdits.php mass rollback) |
||
| (не показано 17 промежуточных версий 6 участников) | |||
| Строка 1: | Строка 1: | ||
| − | + | '''Метод опорных векторов''' (англ. ''support vector machine'', ''SVM'') — один из наиболее популярных методов обучения, который применяется для решения задач классификации и регрессии. Основная идея метода заключается в построении гиперплоскости, разделяющей объекты выборки оптимальным способом. Алгоритм работает в предположении, что чем больше расстояние (зазор) между разделяющей гиперплоскостью и объектами разделяемых классов, тем меньше будет средняя ошибка классификатора. | |
| − | |||
| − | |||
| − | '''Метод опорных векторов''' (англ. ''support vector machine'', ''SVM'') — один из наиболее популярных методов обучения, который применяется для решения задач классификации и регрессии. Основная идея метода заключается в построении гиперплоскости, разделяющей объекты выборки | ||
== Метод опорных векторов в задаче классификации == | == Метод опорных векторов в задаче классификации == | ||
| Строка 16: | Строка 13: | ||
В пространстве $\mathbb{R}^n$ уравнение $\langle \vec{w}, \vec{x} \rangle - b = 0$ при заданных $\vec{w}$ и $b$ определяет гиперплоскость — множество векторов $\vec{x} = (x_1, \ldots, x_n)$, принадлежащих пространству меньшей размерности $\mathbb{R}^{n-1}$. Например, для $\mathbb{R}^1$ гиперплоскостью является точка, для $\mathbb{R}^2$ — прямая, для $\mathbb{R}^3$ — плоскость и т.д. Параметр $\vec{w}$ определяет вектор нормали к гиперплоскости, а через $\frac{b}{\lVert \vec{w} \rVert}$ выражается расстояние от гиперплоскости до начала координат. | В пространстве $\mathbb{R}^n$ уравнение $\langle \vec{w}, \vec{x} \rangle - b = 0$ при заданных $\vec{w}$ и $b$ определяет гиперплоскость — множество векторов $\vec{x} = (x_1, \ldots, x_n)$, принадлежащих пространству меньшей размерности $\mathbb{R}^{n-1}$. Например, для $\mathbb{R}^1$ гиперплоскостью является точка, для $\mathbb{R}^2$ — прямая, для $\mathbb{R}^3$ — плоскость и т.д. Параметр $\vec{w}$ определяет вектор нормали к гиперплоскости, а через $\frac{b}{\lVert \vec{w} \rVert}$ выражается расстояние от гиперплоскости до начала координат. | ||
| − | Гиперплоскость делит $\mathbb{R}^n$ на два полупространства: $\langle \vec{w}, \vec{x} \rangle - b > 0$ и $\langle \vec{w}, \vec{x} \rangle - b < 0$. | + | Гиперплоскость делит $\mathbb{R}^n$ на два полупространства: $\langle \vec{w}, \vec{x} \rangle - b > 0$ и $\langle \vec{w}, \vec{x} \rangle - b < 0$. |
Говорят, что гиперплоскость разделяет два класса $C_1$ и $C_2$, если объекты этих классов лежат по разные стороны от гиперплоскости, то есть выполнено либо | Говорят, что гиперплоскость разделяет два класса $C_1$ и $C_2$, если объекты этих классов лежат по разные стороны от гиперплоскости, то есть выполнено либо | ||
| Строка 34: | Строка 31: | ||
где $\vec{x} = (x_1, \ldots, x_n)$ — вектор значений признаков объекта, а $\vec{w} = (w_1, \ldots, w_n) \in \mathbb{R}^n$ и $b \in \mathbb{R}$ — параметры гиперплоскости. | где $\vec{x} = (x_1, \ldots, x_n)$ — вектор значений признаков объекта, а $\vec{w} = (w_1, \ldots, w_n) \in \mathbb{R}^n$ и $b \in \mathbb{R}$ — параметры гиперплоскости. | ||
| − | Но для двух линейно разделимых классов | + | Но для двух линейно разделимых классов возможны различные варианты построения разделяющих гиперплоскостей. Метод опорных векторов выбирает ту гиперплоскость, которая максимизирует отступ между классами: |
{{Определение | {{Определение | ||
| − | |definition='''Отступ''' (англ. ''margin'') — характеристика, оценивающая, насколько объект "погружён" в свой класс, насколько типичным представителем класса он является. Чем меньше значение отступа $M_i$, тем ближе объект $\vec{x}_i$ подходит к границе классов и тем выше становится вероятность ошибки. Отступ $M_i$ отрицателен тогда и только тогда, когда алгоритм $a(x)$ допускает ошибку на объекте $\vec{x}_i$. | + | |definition= |
| − | Для | + | '''Отступ''' (англ. ''margin'') — характеристика, оценивающая, насколько объект "погружён" в свой класс, насколько типичным представителем класса он является. Чем меньше значение отступа $M_i$, тем ближе объект $\vec{x}_i$ подходит к границе классов и тем выше становится вероятность ошибки. Отступ $M_i$ отрицателен тогда и только тогда, когда алгоритм $a(x)$ допускает ошибку на объекте $\vec{x}_i$. <br><br> Для линейного классификатора отступ определяется уравнением: $M_i(\vec{w}, b) = y_i(\langle \vec{w}, \vec{x}_i \rangle - b)$ |
| − | |||
}} | }} | ||
| + | Если выборка линейно разделима, то существует такая гиперплоскость, отступ от которой до каждого объекта положителен: | ||
| + | |||
| + | $\exists \vec{w}, b : \; M_i(\vec{w}, b) = y_i(\langle \vec{w}, \vec{x}_i \rangle - b) > 0, \; i = 1\ldots\ell$ | ||
| + | |||
| + | Мы хотим построить такую разделяющую гиперплоскость, чтобы объекты обучающей выборки находились на наибольшем расстоянии от неё. | ||
| + | |||
| + | [[Файл:SVM_margin.png|300px|thumb|right|Оптимальная разделяющая гиперплоскость в $\mathbb{R}^2$]] | ||
| + | Заметим, что при умножении $\vec{w}$ и $b$ на константу $c \neq 0$ уравнение $\langle c\vec{w}, \vec{x} \rangle - cb = 0$ определяет ту же самую гиперплоскость, что и $\langle \vec{w}, \vec{x} \rangle - b = 0$. Для удобства проведём нормировку: выберем константу $c$ таким образом, чтобы $\min M_i(\vec{w}, b) = 1$. При этом в каждом из двух классов найдётся хотя бы один "граничный" объект обучающей выборки, отступ которого равен этому минимуму: иначе можно было бы сместить гиперплоскость в сторону класса с большим отступом, тем самым увеличив минимальное расстояние от гиперплоскости до объектов обучающей выборки. | ||
| + | |||
| + | Обозначим любой "граничный" объект из класса $+1$ как $\vec{x}_+$, из класса $-1$ как $\vec{x}_-$. Их отступ равен единице, то есть | ||
| + | |||
| + | $\begin{cases} | ||
| + | M_+(\vec{w}, b) = (+1)(\langle \vec{w}, \vec{x}_+ \rangle - b) = 1 \\ | ||
| + | M_-(\vec{w}, b) = (-1)(\langle \vec{w}, \vec{x}_- \rangle - b) = 1 | ||
| + | \end{cases}$ | ||
| + | |||
| + | Нормировка позволяет ограничить разделяющую полосу между классами: $\{x: -1 < \langle \vec{w}, \vec{x}_i \rangle - b < 1\}$. Внутри неё не может лежать ни один объект обучающей выборки. Ширину разделяющей полосы можно выразить как проекцию вектора $\vec{x}_+ - \vec{x}_-$ на нормаль к гиперплоскости $\vec{w}$. Чтобы разделяющая гиперплоскость находилась на наибольшем расстоянии от точек выборки, ширина полосы должна быть максимальной: | ||
| + | |||
| + | $\frac{\langle \vec{x}_+ - \vec{x}_-, \vec{w} \rangle}{\lVert w \rVert} = \frac{\langle \vec{x}_+, \vec{w} \rangle - \langle \vec{x}_-, \vec{w} \rangle - b + b}{\lVert w \rVert} = \frac{(+1)\left(\langle \vec{x}_+, \vec{w} \rangle - b\right) \, + \, (-1)\left(\langle \vec{x}_-, \vec{w} \rangle - b\right)}{\lVert w \rVert} = \\ = \frac{M_+(\vec{w}, b) \, + \, M_-(\vec{w}, b)}{\lVert w \rVert} = \frac{2}{\lVert w \rVert} \to \max \; \Rightarrow \; \lVert w \rVert \to \min$ | ||
| + | |||
| + | Это приводит нас к постановке задачи оптимизации в терминах квадратичного программирования: | ||
| + | |||
| + | $\begin{cases} | ||
| + | \lVert \vec{w} \rVert^2 \to \min\limits_{w,b} \\ | ||
| + | M_i(\vec{w}, b) \geq 1, \quad i = 1, \ldots, \ell | ||
| + | \end{cases}$ | ||
| + | |||
| + | === Линейно неразделимая выборка === | ||
| + | |||
| + | На практике линейно разделимые выборки практически не встречаются: в данных возможны выбросы и нечёткие границы между классами. В таком случае поставленная выше задача не имеет решений, и необходимо ослабить ограничения, позволив некоторым объектам попадать на "территорию" другого класса. Для каждого объекта отнимем от отступа некоторую положительную величину $\xi_i$, но потребуем чтобы эти введённые поправки были минимальны. Это приведёт к следующей постановке задачи, называемой также ''SVM с мягким отступом'' (англ. ''soft-margin SVM''): | ||
| + | |||
| + | $\begin{cases} | ||
| + | \frac{1}{2} \lVert \vec{w} \rVert^2 \color{brown}{+ C \sum\limits_{i=1}^\ell \xi_i} \to \min\limits_{w, b, \color{brown}{\xi}} \\ | ||
| + | M_i(\vec{w}, b) \geq 1 \color{brown}{- \xi_i}, \quad i = 1, \ldots, \ell \\ | ||
| + | \color{brown}{\xi_i \geq 0, \quad i = 1, \ldots, \ell} \\ | ||
| + | \end{cases}$ | ||
| − | + | Мы не знаем, какой из функционалов $\frac{1}{2} \lVert \vec{w} \rVert^2$ и $\sum\limits_{i=1}^\ell \xi_i$ важнее, поэтому вводим коэффициент $C$, который будем оптимизировать с помощью кросс-валидации. В итоге мы получили задачу, у которой всегда есть единственное решение. | |
| − | + | Заметим, что мы можем упростить постановку задачи: | |
| + | $\begin{cases} | ||
| + | \xi_i \geq 0 \\ | ||
| + | \xi_i \geq 1 - M_i(\vec{w}, b) \\ | ||
| + | \sum\limits_{i=1}^\ell \xi_i \to \min | ||
| + | \end{cases} | ||
| + | \,\Rightarrow\, | ||
| + | \begin{cases} | ||
| + | \xi_i \geq \max(0, 1 - M_i(\vec{w}, b)) \\ | ||
| + | \sum\limits_{i=1}^\ell \xi_i \to \min | ||
| + | \end{cases} | ||
| + | \,\Rightarrow\, | ||
| + | \xi_i = (1- M_i(\vec{w}, b))_+$ | ||
| − | + | Получим эквивалентную задачу безусловной минимизации: | |
| + | $\frac{1}{2} \lVert \vec{w} \rVert^2 + C \sum\limits_{i=1}^\ell \left(1 - M_i(\vec{w}, b)\right)_+ \to \min\limits_{w, b}$ | ||
| + | Теперь научимся её решать. | ||
{{Теорема | {{Теорема | ||
| Строка 63: | Строка 109: | ||
$$ | $$ | ||
| − | Если $ | + | Если $x$ — точка локального минимума при наложенных ограничениях, то существуют такие множители $\mu_i, i = 1\ldots m$, $\;\lambda_j, j = 1\ldots k$, что для функции Лагранжа $L(x; \mu, \lambda)$ выполняются условия: |
| − | $$\begin{cases}\frac{\partial L}{\partial x} = 0 \quad L(x; \mu, \lambda) = f(x) + \sum\limits_{i=1}^m \mu_i g_i(x) + \sum\limits_{j=1}^k \lambda_j h_j(x) \\ g_i(x) \leq 0,\;h_j(x) = 0 \quad \text{(исходные ограничения)} \\ \mu_i \geq 0 \quad \text{(двойственные ограничения)} \\ \mu_i g_i(x) = 0 \quad \text{(условие дополняющей нежёсткости)} \end{cases}$$ | + | $$\begin{cases}\frac{\partial L}{\partial x} = 0, \quad L(x; \mu, \lambda) = f(x) + \sum\limits_{i=1}^m \mu_i g_i(x) + \sum\limits_{j=1}^k \lambda_j h_j(x) \\ g_i(x) \leq 0,\;h_j(x) = 0 \quad \text{(исходные ограничения)} \\ \mu_i \geq 0 \quad \text{(двойственные ограничения)} \\ \mu_i g_i(x) = 0 \quad \text{(условие дополняющей нежёсткости)} \end{cases}$$ |
| + | |||
| + | При этом искомая точка является седловой точкой функции Лагранжа: минимумом по $x$ и максимумом по двойственным переменным $\mu$. | ||
}} | }} | ||
| + | По теореме Каруша—Куна—Таккера, поставленная нами задача минимизации эквивалентна двойственной задаче поиска седловой точки функции Лагранжа: | ||
| + | |||
| + | $\mathscr{L}(\vec{w},b,\xi; \lambda, \eta) = \frac{1}{2} \lVert w \rVert^2 - \sum\limits_{i=1}^\ell \lambda_i \left(M_i(\vec{w}, b) - 1\right) - \sum\limits_{i=1}^\ell \xi_i \left(\lambda_i + \eta_i - C\right)$ | ||
| + | |||
| + | $\lambda_i$ — переменные, двойственные к ограничениям $M_i \geq 1 - \xi_i$ | ||
| + | |||
| + | $\eta_i$ — переменные, двойственные к ограничениям $\xi_i \geq 0$ | ||
| + | |||
| + | |||
| + | Запишем необходимые условия седловой точки функции Лагранжа: | ||
| + | $\begin{cases} | ||
| + | \frac{\partial \mathscr{L}}{\partial w} = 0, \quad \frac{\partial \mathscr{L}}{\partial b} = 0, \quad \frac{\partial \mathscr{L}}{\partial \xi} = 0 \\ | ||
| + | \xi_i \geq 0, \quad \lambda_i \geq 0, \quad \eta_i \geq 0, && i = 1, \ldots, \ell \\ | ||
| + | \lambda_i = 0 \;\text{либо}\; M_i(\vec{w},b) = 1 - \xi_i, && i = 1, \ldots, \ell \\ | ||
| + | \eta_i = 0 \;\text{либо}\; \xi_i = 0, && i = 1, \ldots, \ell | ||
| + | \end{cases}$ | ||
| − | |||
| − | + | Продифференцируем функцию Лагранжа и приравняем к нулю производные. Получим следующие ограничения: | |
| − | $\sum\limits_{i=1}^\ell | + | $\begin{array}{lcl} |
| + | \frac{\partial \mathscr{L}}{\partial w} = \vec{w} - \sum\limits_{i=1}^\ell \lambda_i y_i \vec{x}_i = 0 & \Rightarrow & \vec{w} = \sum\limits_{i=1}^\ell \lambda_i y_i \vec{x}_i \\ | ||
| + | \frac{\partial \mathscr{L}}{\partial b} = -\sum\limits_{i=1}^\ell \lambda_i y_i = 0 & \Rightarrow & \sum\limits_{i=1}^\ell \lambda_i y_i = 0 \\ | ||
| + | \frac{\partial \mathscr{L}}{\partial \xi_i} = -\lambda_i - \eta_i + C = 0 & \Rightarrow & \eta_i + \lambda_i = C, \quad i = 1, \ldots, \ell | ||
| + | \end{array}$ | ||
| + | Заметим, что $\eta_i \geq 0$, $\lambda_i \geq 0$, $C > 0$, поэтому из последнего ограничения получаем $0 \leq \eta_i \leq C$, $0 \leq \lambda_i \leq C$. | ||
| − | === | + | Диапазон значений $\lambda_i$ (которые, как указано выше, соответствуют ограничениям на величину отступа) позволяет нам разделить объекты обучающей выборки на три типа: |
| + | |||
| + | # $\lambda_i = 0 \; \Rightarrow \; \eta_i = C; \; \xi_i = 0; \; M_i \geq 1 \;$ — периферийные (неинформативные) объекты <br> Эти объекты лежат в своём классе, классифицируются верно и не влияют на выбор разделяющей гиперплоскости (см. уравнение для $\vec{w}$) | ||
| + | # $0 < \lambda_i < C \; \Rightarrow \; 0 < \eta_i < C; \; \xi_i = 0; \; M_i = 1 \;$ — опорные граничные объекты <br> Эти объекты лежат ровно на границе разделяющей полосы на стороне своего класса | ||
| + | # $\lambda_i = C \; \Rightarrow \; \eta_i = 0; \; \xi_i > 0; \; M_i < 1 \;$ — опорные объекты-нарушители <br> Эти объекты лежат внутри разделяющей полосы или на стороне чужого класса | ||
| + | |||
| + | {{Определение | ||
| + | |definition= | ||
| + | '''Опорный объект''' (опорный вектор, англ. ''support vector'') — объект $\vec{x}_i$, соответствующий которому множитель Лагранжа отличен от нуля: $\lambda_i \neq 0$. | ||
| + | }} | ||
| + | |||
| + | Теперь подставим ограничения, которые мы получили при дифференцировании, в функцию Лагранжа. Получим следующую постановку двойственной задачи, которая зависит только от двойственных переменных $\lambda$: | ||
| + | |||
| + | $\begin{cases} | ||
| + | -\mathscr{L}(\lambda) = -\sum\limits_{i=1}^\ell \lambda_i + \frac{1}{2} \sum\limits_{i=1}^\ell \sum\limits_{j=1}^\ell \lambda_i \lambda_j y_i y_j \langle \vec{x}_i, \vec{x}_j \rangle \to \min\limits_\lambda \\ | ||
| + | 0 \leq \lambda_i \leq C, \quad i = 1, \ldots, \ell \\ | ||
| + | \sum\limits_{i=1}^\ell \lambda_i y_i = 0 | ||
| + | \end{cases}$ | ||
| + | |||
| + | Это также задача квадратичного программирования. Решение задачи лежит в пересечении $\ell$-мерного куба с ребром $C$ и гиперплоскости $\langle \lambda, y \rangle = 0$, что является выпуклым многогранником размерности $\ell-1$. В этом многограннике нужно найти минимум выпуклого квадратичного функционала. Следовательно, данная задача имеет единственное решение. | ||
| + | |||
| + | Существуют различные методы поиска решения: можно воспользоваться универсальным солвером задачи квадратичного программирования ([https://www.ibm.com/analytics/cplex-optimizer CPLEX], [http://www.gurobi.com/ Gurobi]), либо алгоритмом, учитывающим специфические особенности SVM ([https://www.microsoft.com/en-us/research/publication/sequential-minimal-optimization-a-fast-algorithm-for-training-support-vector-machines/ SMO], [http://citeseerx.ist.psu.edu/viewdoc/summary?doi=10.1.1.10.9956 INCAS]). | ||
| + | |||
| + | После того, как мы получили вектор коэффициентов $\vec{\lambda}$, можем выразить решение прямой задачи через решение двойственной: | ||
| + | |||
| + | $\begin{cases} | ||
| + | \vec{w} = \sum\limits_{i=1}^\ell \lambda_i y_i \vec{x}_i \\ | ||
| + | b = \langle \vec{w}, \vec{x}_i \rangle - y_i, \quad \forall i: \lambda_i > 0, M_i = 1 | ||
| + | \end{cases}$ | ||
| + | |||
| + | На практике для повышения вычислительной устойчивости рекомендуется при расчёте $b$ брать медиану по опорным граничным объектам: | ||
| + | |||
| + | $b = med\{ \langle \vec{w}, \vec{x}_i \rangle - y_i : \lambda_i > 0, M_i = 1, i = 1, \ldots, \ell\}$ | ||
| + | |||
| + | Теперь можем переписать наш линейный классификатор, выразив $\vec{w}$ через $\vec{\lambda}$: | ||
| + | |||
| + | $a(x) = sign \left(\sum\limits_{i=1}^\ell \lambda_i y_i \langle \vec{x}_i, \vec{x} \rangle - b\right)$ | ||
| + | |||
| + | === Нелинейное обобщение, kernel trick === | ||
| + | |||
| + | Существует ещё один подход к решению проблемы линейной разделимости, известный как трюк с ядром (kernel trick). Если выборка объектов с признаковым описанием из $X = \mathbb{R}^n$ не является линейно разделимой, мы можем предположить, что существует некоторое пространство $H$, вероятно, большей размерности, при переходе в которое выборка станет линейно разделимой. Пространство $H$ здесь называют спрямляющим, а функцию перехода $\psi : X \to H$ — спрямляющим отображением. Построение SVM в таком случае происходит так же, как и раньше, но в качестве векторов признаковых описаний используются векторы $\psi(\vec{x})$, а не $\vec{x}$. Соответственно, скалярное произведение $\langle \vec{x}_1, \vec{x}_2 \rangle$ в пространстве $X$ везде заменяется скалярным произведением $\langle \psi(\vec{x}_1), \psi(\vec{x}_2) \rangle$ в пространстве $H$. Отсюда следует, что пространство $H$ должно быть гильбертовым, так как в нём должно быть определено скалярное произведение. | ||
| + | |||
| + | Обратим внимание на то, что постановка задачи и алгоритм классификации не используют в явном виде признаковое описание и оперируют только скалярными произведениями признаков объектов. Это даёт возможность заменить скалярное произведение в пространстве $X$ на [[Ядра|ядро]] — функцию, являющуюся скалярным произведением в некотором $H$. При этом можно вообще не строить спрямляющее пространство в явном виде, и вместо подбора $\psi$ подбирать непосредственно ядро. | ||
| + | |||
| + | Постановка задачи с применением ядер приобретает вид: | ||
| + | |||
| + | $\begin{cases} | ||
| + | -\mathscr{L}(\lambda) = -\sum\limits_{i=1}^\ell \lambda_i + \frac{1}{2} \sum\limits_{i=1}^\ell \sum\limits_{j=1}^\ell \lambda_i \lambda_j y_i y_j \color{brown}{K(\vec{x}_i, \vec{x}_j)} \to \min\limits_\lambda \\ | ||
| + | 0 \leq \lambda_i \leq C, \quad i = 1, \ldots, \ell \\ | ||
| + | \sum\limits_{i=1}^\ell \lambda_i y_i = 0 | ||
| + | \end{cases}$ | ||
| + | |||
| + | $a(x) = sign \left(\sum\limits_{i=1}^\ell \lambda_i y_i \color{brown}{K(\vec{x}_i, \vec{x})} - b\right)$ | ||
| + | |||
| + | == Преимущества и недостатки SVM == | ||
| + | |||
| + | Преимущества SVM перед методом стохастического градиента и нейронными сетями: | ||
| + | |||
| + | * Задача выпуклого квадратичного программирования хорошо изучена и имеет единственное решение. | ||
| + | * Метод опорных векторов эквивалентен двухслойной нейронной сети, где число нейронов на скрытом слое определяется автоматически как число опорных векторов. | ||
| + | * Принцип оптимальной разделяющей гиперплоскости приводит к максимизации ширины разделяющей полосы, а следовательно, к более уверенной классификации. | ||
| + | |||
| + | Недостатки классического SVM: | ||
| + | |||
| + | * Неустойчивость к шуму: выбросы в исходных данных становятся опорными объектами-нарушителями и напрямую влияют на построение разделяющей гиперплоскости. | ||
| + | * Не описаны общие методы построения ядер и спрямляющих пространств, наиболее подходящих для конкретной задачи. | ||
| + | * Нет отбора признаков. | ||
| + | * Необходимо подбирать константу $C$ при помощи кросс-валидации. | ||
| + | |||
| + | == Модификации == | ||
| + | |||
| + | Существуют различные дополнения и модификации метода опорных векторов, направленные на устранение описанных недостатков: | ||
| + | |||
| + | * [http://jmlr.csail.mit.edu/papers/v1/tipping01a.html Метод релевантных векторов (Relevance Vector Machine, RVM)] | ||
| + | * [https://papers.nips.cc/paper/2450-1-norm-support-vector-machines.pdf 1-norm SVM (LASSO SVM)] | ||
| + | * [http://www3.stat.sinica.edu.tw/statistica/oldpdf/A16n214.pdf Doubly Regularized SVM (ElasticNet SVM)] | ||
| + | * [https://arxiv.org/abs/1901.09643v1 Support Features Machine (SFM)] | ||
| + | * [http://www.robots.ox.ac.uk/~minhhoai/papers/SVMFeatureWeight_PR.pdf Relevance Features Machine (RFM)] | ||
| + | ==Примеры кода== | ||
| + | ===Пример на языке Java=== | ||
| + | Пример классификации с применением <code>smile.classification.SVM</code><ref>[https://haifengl.github.io/smile/api/java/smile/classification/SVM.html/ Smile, SVM]</ref> | ||
| + | <code>Maven</code> зависимость: | ||
| + | <dependency> | ||
| + | <groupId>com.github.haifengl</groupId> | ||
| + | <artifactId>smile-core</artifactId> | ||
| + | <version>1.5.2</version> | ||
| + | </dependency> | ||
| + | '''import''' smile.classification.SVM; | ||
| + | '''import''' smile.data.NominalAttribute; | ||
| + | '''import''' smile.data.parser.DelimitedTextParser; | ||
| + | '''import''' smile.math.kernel.GaussianKernel; | ||
| + | '''import''' java.util.Arrays; | ||
| + | <font color="green">// read train & test dataset</font> | ||
| + | '''var''' parser = new DelimitedTextParser(); | ||
| + | parser.setResponseIndex(new NominalAttribute("class"), 0); | ||
| + | '''var''' train = parser.parse("USPS Train", this.getClass().getResourceAsStream("/smile/data/usps/zip.train")); | ||
| + | '''var''' test = parser.parse("USPS Test", this.getClass().getResourceAsStream("/smile/data/usps/zip.test")); | ||
| + | '''var''' classes = Arrays.stream(test.labels()).max().orElse(0) + 1; | ||
| + | <font color="green">// build SVM classifier</font> | ||
| + | '''var''' svm = new SVM<>(new GaussianKernel(8.0), 5.0, classes, SVM.Multiclass.ONE_VS_ONE); | ||
| + | svm.learn(train.x(), train.labels()); | ||
| + | svm.finish(); | ||
| + | <font color="green">// calculate test error rate</font> | ||
| + | '''var''' error = 0; | ||
| + | for (int i = 0; i < test.x().length; i++) { | ||
| + | if (svm.predict(test.x()[i]) != test.labels()[i]) { | ||
| + | error++; | ||
| + | } | ||
| + | } | ||
| + | System.out.format("USPS error rate = %.2f%%\n", 100.0 * error / test.x().length); | ||
| + | === Пример на языке R === | ||
| + | {{Main|Примеры кода на R}} | ||
| − | == | + | <font color="gray"># importing package and its' dependencies</font> |
| − | // | + | library(caret) |
| + | |||
| + | <font color="gray">#reading data</font> | ||
| + | data <- read.csv(<font color="green">"input.csv"</font>, <font color="#660099">sep</font> = <font color="green">','</font>, <font color="#660099">header</font> = FALSE) | ||
| + | |||
| + | <font color="gray"># splitting data into train and test sets</font> | ||
| + | index <- createDataPartition(<font color="#660099">y</font> = data$<strong><font color="#660E7A">target</font></strong>, <font color="#660099">p</font> = <font color="blue">0.8</font>, <font color="#660099">list</font> = FALSE) | ||
| + | training <- data[index,] | ||
| + | testing <- data[-index,] | ||
| + | |||
| + | <font color="gray"># evaluating model</font> | ||
| + | fit <- train(target ~ x + y + z, | ||
| + | <font color="#660099">data</font> = train_flats, | ||
| + | <font color="#660099">method</font> = <font color="green">"svmRadial"</font>, | ||
| + | <font color="#660099">trControl</font> = trainControl(<font color="#660099">method</font> = <font color="green">"repeatedcv"</font>, <font color="#660099">number</font> = <font color="blue">10</font>, <font color="#660099">repeats</font> = <font color="blue">3</font>)) | ||
| + | |||
| + | <font color="gray"># printing parameters</font> | ||
| + | print(fit) | ||
== См. также == | == См. также == | ||
| + | * [[Общие понятия]] | ||
| + | * [[Ядра]] | ||
* [[Обзор библиотек для машинного обучения на Python]] | * [[Обзор библиотек для машинного обучения на Python]] | ||
| − | |||
== Примечания == | == Примечания == | ||
| Строка 96: | Строка 293: | ||
== Источники информации == | == Источники информации == | ||
| − | * [http://www.machinelearning.ru/wiki/index.php?title=%D0%9C%D0%B0%D1%88%D0%B8%D0%BD%D0%B0_%D0%BE%D0%BF%D0%BE%D1%80%D0%BD%D1%8B%D1%85_%D0%B2%D0%B5%D0%BA%D1%82%D0%BE%D1%80%D0%BE%D0%B2 machinelearning.ru | + | * [http://www.machinelearning.ru/wiki/index.php?title=%D0%9C%D0%B0%D1%88%D0%B8%D0%BD%D0%B0_%D0%BE%D0%BF%D0%BE%D1%80%D0%BD%D1%8B%D1%85_%D0%B2%D0%B5%D0%BA%D1%82%D0%BE%D1%80%D0%BE%D0%B2 machinelearning.ru — Машина опорных векторов] |
| − | * [https://www.youtube.com/watch?v=Adi67_94_gc&list=PLJOzdkh8T5kp99tGTEFjH_b9zqEQiiBtC&index=5 Лекция "Линейные методы классификации: метод опорных векторов"] | + | * [https://www.youtube.com/watch?v=Adi67_94_gc&list=PLJOzdkh8T5kp99tGTEFjH_b9zqEQiiBtC&index=5 Лекция "Линейные методы классификации: метод опорных векторов"] — К.В. Воронцов, курс "Машинное обучение" 2014 |
| − | * [https://ru.wikipedia.org/wiki/%D0%9C%D0%B5%D1%82%D0%BE%D0%B4_%D0%BE%D0%BF%D0%BE%D1%80%D0%BD%D1%8B%D1%85_%D0%B2%D0%B5%D0%BA%D1%82%D0%BE%D1%80%D0%BE%D0%B2 Wikipedia | + | * [https://ru.wikipedia.org/wiki/%D0%9C%D0%B5%D1%82%D0%BE%D0%B4_%D0%BE%D0%BF%D0%BE%D1%80%D0%BD%D1%8B%D1%85_%D0%B2%D0%B5%D0%BA%D1%82%D0%BE%D1%80%D0%BE%D0%B2 Wikipedia — Метод опорных векторов] |
| − | * Alexey Nefedov | + | * Alexey Nefedov — [https://svmtutorial.online/ Support Vector Machines: A Simple Tutorial] |
| − | * John Platt | + | * John Platt — [https://www.microsoft.com/en-us/research/publication/sequential-minimal-optimization-a-fast-algorithm-for-training-support-vector-machines/ Sequential Minimal Optimization: A Fast Algorithm for Training Support Vector Machines] |
| + | * Shai Fine, Katya Scheinberg — [http://citeseerx.ist.psu.edu/viewdoc/summary?doi=10.1.1.10.9956 INCAS: An Incremental Active Set Method for SVM] | ||
[[Категория: Машинное обучение]] | [[Категория: Машинное обучение]] | ||
[[Категория: Классификация]] | [[Категория: Классификация]] | ||
[[Категория: Регрессия]] | [[Категория: Регрессия]] | ||
Текущая версия на 19:06, 4 сентября 2022
Метод опорных векторов (англ. support vector machine, SVM) — один из наиболее популярных методов обучения, который применяется для решения задач классификации и регрессии. Основная идея метода заключается в построении гиперплоскости, разделяющей объекты выборки оптимальным способом. Алгоритм работает в предположении, что чем больше расстояние (зазор) между разделяющей гиперплоскостью и объектами разделяемых классов, тем меньше будет средняя ошибка классификатора.
Содержание
Метод опорных векторов в задаче классификации
Рассмотрим задачу бинарной классификации, в которой объектам из $X=\mathbb{R}^n$ соответствует один из двух классов $Y = \{-1, +1\}$.
Пусть задана обучающая выборка пар "объект-ответ": $T^\ell = (\vec{x}_i, y_i)_{i=1}^\ell$. Необходимо построить алгоритм классификации $a(\vec{x}) : X \to Y$.
Разделяющая гиперплоскость
В пространстве $\mathbb{R}^n$ уравнение $\langle \vec{w}, \vec{x} \rangle - b = 0$ при заданных $\vec{w}$ и $b$ определяет гиперплоскость — множество векторов $\vec{x} = (x_1, \ldots, x_n)$, принадлежащих пространству меньшей размерности $\mathbb{R}^{n-1}$. Например, для $\mathbb{R}^1$ гиперплоскостью является точка, для $\mathbb{R}^2$ — прямая, для $\mathbb{R}^3$ — плоскость и т.д. Параметр $\vec{w}$ определяет вектор нормали к гиперплоскости, а через $\frac{b}{\lVert \vec{w} \rVert}$ выражается расстояние от гиперплоскости до начала координат.
Гиперплоскость делит $\mathbb{R}^n$ на два полупространства: $\langle \vec{w}, \vec{x} \rangle - b > 0$ и $\langle \vec{w}, \vec{x} \rangle - b < 0$.
Говорят, что гиперплоскость разделяет два класса $C_1$ и $C_2$, если объекты этих классов лежат по разные стороны от гиперплоскости, то есть выполнено либо
$\begin{cases}\langle \vec{w}, \vec{x} \rangle - b > 0, && \forall x \in C_1 \\ \langle \vec{w}, \vec{x} \rangle - b < 0, && \forall x \in C_2\end{cases}$
либо
$\begin{cases}\langle \vec{w}, \vec{x} \rangle - b < 0, && \forall x \in C_1 \\ \langle \vec{w}, \vec{x} \rangle - b > 0, && \forall x \in C_2\end{cases}$
Линейно разделимая выборка
Пусть выборка линейно разделима, то есть существует некоторая гиперплоскость, разделяющая классы $-1$ и $+1$. Тогда в качестве алгоритма классификации можно использовать линейный пороговый классификатор:
$a(\vec{x}) = sign(\langle \vec{w}, \vec{x} \rangle - b) = sign\left(\sum\limits_{i=1}^\ell w_i x_i - b\right)$
где $\vec{x} = (x_1, \ldots, x_n)$ — вектор значений признаков объекта, а $\vec{w} = (w_1, \ldots, w_n) \in \mathbb{R}^n$ и $b \in \mathbb{R}$ — параметры гиперплоскости.
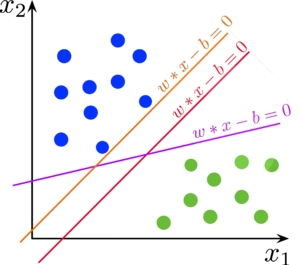
Но для двух линейно разделимых классов возможны различные варианты построения разделяющих гиперплоскостей. Метод опорных векторов выбирает ту гиперплоскость, которая максимизирует отступ между классами:
| Определение: |
| Отступ (англ. margin) — характеристика, оценивающая, насколько объект "погружён" в свой класс, насколько типичным представителем класса он является. Чем меньше значение отступа $M_i$, тем ближе объект $\vec{x}_i$ подходит к границе классов и тем выше становится вероятность ошибки. Отступ $M_i$ отрицателен тогда и только тогда, когда алгоритм $a(x)$ допускает ошибку на объекте $\vec{x}_i$. Для линейного классификатора отступ определяется уравнением: $M_i(\vec{w}, b) = y_i(\langle \vec{w}, \vec{x}_i \rangle - b)$ |
Если выборка линейно разделима, то существует такая гиперплоскость, отступ от которой до каждого объекта положителен:
$\exists \vec{w}, b : \; M_i(\vec{w}, b) = y_i(\langle \vec{w}, \vec{x}_i \rangle - b) > 0, \; i = 1\ldots\ell$
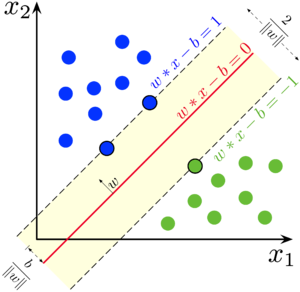
Мы хотим построить такую разделяющую гиперплоскость, чтобы объекты обучающей выборки находились на наибольшем расстоянии от неё.
Заметим, что при умножении $\vec{w}$ и $b$ на константу $c \neq 0$ уравнение $\langle c\vec{w}, \vec{x} \rangle - cb = 0$ определяет ту же самую гиперплоскость, что и $\langle \vec{w}, \vec{x} \rangle - b = 0$. Для удобства проведём нормировку: выберем константу $c$ таким образом, чтобы $\min M_i(\vec{w}, b) = 1$. При этом в каждом из двух классов найдётся хотя бы один "граничный" объект обучающей выборки, отступ которого равен этому минимуму: иначе можно было бы сместить гиперплоскость в сторону класса с большим отступом, тем самым увеличив минимальное расстояние от гиперплоскости до объектов обучающей выборки.
Обозначим любой "граничный" объект из класса $+1$ как $\vec{x}_+$, из класса $-1$ как $\vec{x}_-$. Их отступ равен единице, то есть
$\begin{cases} M_+(\vec{w}, b) = (+1)(\langle \vec{w}, \vec{x}_+ \rangle - b) = 1 \\ M_-(\vec{w}, b) = (-1)(\langle \vec{w}, \vec{x}_- \rangle - b) = 1 \end{cases}$
Нормировка позволяет ограничить разделяющую полосу между классами: $\{x: -1 < \langle \vec{w}, \vec{x}_i \rangle - b < 1\}$. Внутри неё не может лежать ни один объект обучающей выборки. Ширину разделяющей полосы можно выразить как проекцию вектора $\vec{x}_+ - \vec{x}_-$ на нормаль к гиперплоскости $\vec{w}$. Чтобы разделяющая гиперплоскость находилась на наибольшем расстоянии от точек выборки, ширина полосы должна быть максимальной:
$\frac{\langle \vec{x}_+ - \vec{x}_-, \vec{w} \rangle}{\lVert w \rVert} = \frac{\langle \vec{x}_+, \vec{w} \rangle - \langle \vec{x}_-, \vec{w} \rangle - b + b}{\lVert w \rVert} = \frac{(+1)\left(\langle \vec{x}_+, \vec{w} \rangle - b\right) \, + \, (-1)\left(\langle \vec{x}_-, \vec{w} \rangle - b\right)}{\lVert w \rVert} = \\ = \frac{M_+(\vec{w}, b) \, + \, M_-(\vec{w}, b)}{\lVert w \rVert} = \frac{2}{\lVert w \rVert} \to \max \; \Rightarrow \; \lVert w \rVert \to \min$
Это приводит нас к постановке задачи оптимизации в терминах квадратичного программирования:
$\begin{cases} \lVert \vec{w} \rVert^2 \to \min\limits_{w,b} \\ M_i(\vec{w}, b) \geq 1, \quad i = 1, \ldots, \ell \end{cases}$
Линейно неразделимая выборка
На практике линейно разделимые выборки практически не встречаются: в данных возможны выбросы и нечёткие границы между классами. В таком случае поставленная выше задача не имеет решений, и необходимо ослабить ограничения, позволив некоторым объектам попадать на "территорию" другого класса. Для каждого объекта отнимем от отступа некоторую положительную величину $\xi_i$, но потребуем чтобы эти введённые поправки были минимальны. Это приведёт к следующей постановке задачи, называемой также SVM с мягким отступом (англ. soft-margin SVM):
$\begin{cases} \frac{1}{2} \lVert \vec{w} \rVert^2 \color{brown}{+ C \sum\limits_{i=1}^\ell \xi_i} \to \min\limits_{w, b, \color{brown}{\xi}} \\ M_i(\vec{w}, b) \geq 1 \color{brown}{- \xi_i}, \quad i = 1, \ldots, \ell \\ \color{brown}{\xi_i \geq 0, \quad i = 1, \ldots, \ell} \\ \end{cases}$
Мы не знаем, какой из функционалов $\frac{1}{2} \lVert \vec{w} \rVert^2$ и $\sum\limits_{i=1}^\ell \xi_i$ важнее, поэтому вводим коэффициент $C$, который будем оптимизировать с помощью кросс-валидации. В итоге мы получили задачу, у которой всегда есть единственное решение.
Заметим, что мы можем упростить постановку задачи:
$\begin{cases} \xi_i \geq 0 \\ \xi_i \geq 1 - M_i(\vec{w}, b) \\ \sum\limits_{i=1}^\ell \xi_i \to \min \end{cases} \,\Rightarrow\, \begin{cases} \xi_i \geq \max(0, 1 - M_i(\vec{w}, b)) \\ \sum\limits_{i=1}^\ell \xi_i \to \min \end{cases} \,\Rightarrow\, \xi_i = (1- M_i(\vec{w}, b))_+$
Получим эквивалентную задачу безусловной минимизации:
$\frac{1}{2} \lVert \vec{w} \rVert^2 + C \sum\limits_{i=1}^\ell \left(1 - M_i(\vec{w}, b)\right)_+ \to \min\limits_{w, b}$
Теперь научимся её решать.
| Теорема (Условия Каруша—Куна—Таккера): |
Пусть поставлена задача нелинейного программирования с ограничениями:
$$ \begin{cases} f(x) \to \min\limits_{x \in X} \\ g_i(x) \leq 0,\;i=1\ldots m \\ h_j(x) = 0,\;j=1\ldots k \end{cases} $$ Если $x$ — точка локального минимума при наложенных ограничениях, то существуют такие множители $\mu_i, i = 1\ldots m$, $\;\lambda_j, j = 1\ldots k$, что для функции Лагранжа $L(x; \mu, \lambda)$ выполняются условия: $$\begin{cases}\frac{\partial L}{\partial x} = 0, \quad L(x; \mu, \lambda) = f(x) + \sum\limits_{i=1}^m \mu_i g_i(x) + \sum\limits_{j=1}^k \lambda_j h_j(x) \\ g_i(x) \leq 0,\;h_j(x) = 0 \quad \text{(исходные ограничения)} \\ \mu_i \geq 0 \quad \text{(двойственные ограничения)} \\ \mu_i g_i(x) = 0 \quad \text{(условие дополняющей нежёсткости)} \end{cases}$$ При этом искомая точка является седловой точкой функции Лагранжа: минимумом по $x$ и максимумом по двойственным переменным $\mu$. |
По теореме Каруша—Куна—Таккера, поставленная нами задача минимизации эквивалентна двойственной задаче поиска седловой точки функции Лагранжа:
$\mathscr{L}(\vec{w},b,\xi; \lambda, \eta) = \frac{1}{2} \lVert w \rVert^2 - \sum\limits_{i=1}^\ell \lambda_i \left(M_i(\vec{w}, b) - 1\right) - \sum\limits_{i=1}^\ell \xi_i \left(\lambda_i + \eta_i - C\right)$
$\lambda_i$ — переменные, двойственные к ограничениям $M_i \geq 1 - \xi_i$
$\eta_i$ — переменные, двойственные к ограничениям $\xi_i \geq 0$
Запишем необходимые условия седловой точки функции Лагранжа:
$\begin{cases} \frac{\partial \mathscr{L}}{\partial w} = 0, \quad \frac{\partial \mathscr{L}}{\partial b} = 0, \quad \frac{\partial \mathscr{L}}{\partial \xi} = 0 \\ \xi_i \geq 0, \quad \lambda_i \geq 0, \quad \eta_i \geq 0, && i = 1, \ldots, \ell \\ \lambda_i = 0 \;\text{либо}\; M_i(\vec{w},b) = 1 - \xi_i, && i = 1, \ldots, \ell \\ \eta_i = 0 \;\text{либо}\; \xi_i = 0, && i = 1, \ldots, \ell \end{cases}$
Продифференцируем функцию Лагранжа и приравняем к нулю производные. Получим следующие ограничения:
$\begin{array}{lcl} \frac{\partial \mathscr{L}}{\partial w} = \vec{w} - \sum\limits_{i=1}^\ell \lambda_i y_i \vec{x}_i = 0 & \Rightarrow & \vec{w} = \sum\limits_{i=1}^\ell \lambda_i y_i \vec{x}_i \\ \frac{\partial \mathscr{L}}{\partial b} = -\sum\limits_{i=1}^\ell \lambda_i y_i = 0 & \Rightarrow & \sum\limits_{i=1}^\ell \lambda_i y_i = 0 \\ \frac{\partial \mathscr{L}}{\partial \xi_i} = -\lambda_i - \eta_i + C = 0 & \Rightarrow & \eta_i + \lambda_i = C, \quad i = 1, \ldots, \ell \end{array}$
Заметим, что $\eta_i \geq 0$, $\lambda_i \geq 0$, $C > 0$, поэтому из последнего ограничения получаем $0 \leq \eta_i \leq C$, $0 \leq \lambda_i \leq C$.
Диапазон значений $\lambda_i$ (которые, как указано выше, соответствуют ограничениям на величину отступа) позволяет нам разделить объекты обучающей выборки на три типа:
- $\lambda_i = 0 \; \Rightarrow \; \eta_i = C; \; \xi_i = 0; \; M_i \geq 1 \;$ — периферийные (неинформативные) объекты
Эти объекты лежат в своём классе, классифицируются верно и не влияют на выбор разделяющей гиперплоскости (см. уравнение для $\vec{w}$) - $0 < \lambda_i < C \; \Rightarrow \; 0 < \eta_i < C; \; \xi_i = 0; \; M_i = 1 \;$ — опорные граничные объекты
Эти объекты лежат ровно на границе разделяющей полосы на стороне своего класса - $\lambda_i = C \; \Rightarrow \; \eta_i = 0; \; \xi_i > 0; \; M_i < 1 \;$ — опорные объекты-нарушители
Эти объекты лежат внутри разделяющей полосы или на стороне чужого класса
| Определение: |
| Опорный объект (опорный вектор, англ. support vector) — объект $\vec{x}_i$, соответствующий которому множитель Лагранжа отличен от нуля: $\lambda_i \neq 0$. |
Теперь подставим ограничения, которые мы получили при дифференцировании, в функцию Лагранжа. Получим следующую постановку двойственной задачи, которая зависит только от двойственных переменных $\lambda$:
$\begin{cases} -\mathscr{L}(\lambda) = -\sum\limits_{i=1}^\ell \lambda_i + \frac{1}{2} \sum\limits_{i=1}^\ell \sum\limits_{j=1}^\ell \lambda_i \lambda_j y_i y_j \langle \vec{x}_i, \vec{x}_j \rangle \to \min\limits_\lambda \\ 0 \leq \lambda_i \leq C, \quad i = 1, \ldots, \ell \\ \sum\limits_{i=1}^\ell \lambda_i y_i = 0 \end{cases}$
Это также задача квадратичного программирования. Решение задачи лежит в пересечении $\ell$-мерного куба с ребром $C$ и гиперплоскости $\langle \lambda, y \rangle = 0$, что является выпуклым многогранником размерности $\ell-1$. В этом многограннике нужно найти минимум выпуклого квадратичного функционала. Следовательно, данная задача имеет единственное решение.
Существуют различные методы поиска решения: можно воспользоваться универсальным солвером задачи квадратичного программирования (CPLEX, Gurobi), либо алгоритмом, учитывающим специфические особенности SVM (SMO, INCAS).
После того, как мы получили вектор коэффициентов $\vec{\lambda}$, можем выразить решение прямой задачи через решение двойственной:
$\begin{cases} \vec{w} = \sum\limits_{i=1}^\ell \lambda_i y_i \vec{x}_i \\ b = \langle \vec{w}, \vec{x}_i \rangle - y_i, \quad \forall i: \lambda_i > 0, M_i = 1 \end{cases}$
На практике для повышения вычислительной устойчивости рекомендуется при расчёте $b$ брать медиану по опорным граничным объектам:
$b = med\{ \langle \vec{w}, \vec{x}_i \rangle - y_i : \lambda_i > 0, M_i = 1, i = 1, \ldots, \ell\}$
Теперь можем переписать наш линейный классификатор, выразив $\vec{w}$ через $\vec{\lambda}$:
$a(x) = sign \left(\sum\limits_{i=1}^\ell \lambda_i y_i \langle \vec{x}_i, \vec{x} \rangle - b\right)$
Нелинейное обобщение, kernel trick
Существует ещё один подход к решению проблемы линейной разделимости, известный как трюк с ядром (kernel trick). Если выборка объектов с признаковым описанием из $X = \mathbb{R}^n$ не является линейно разделимой, мы можем предположить, что существует некоторое пространство $H$, вероятно, большей размерности, при переходе в которое выборка станет линейно разделимой. Пространство $H$ здесь называют спрямляющим, а функцию перехода $\psi : X \to H$ — спрямляющим отображением. Построение SVM в таком случае происходит так же, как и раньше, но в качестве векторов признаковых описаний используются векторы $\psi(\vec{x})$, а не $\vec{x}$. Соответственно, скалярное произведение $\langle \vec{x}_1, \vec{x}_2 \rangle$ в пространстве $X$ везде заменяется скалярным произведением $\langle \psi(\vec{x}_1), \psi(\vec{x}_2) \rangle$ в пространстве $H$. Отсюда следует, что пространство $H$ должно быть гильбертовым, так как в нём должно быть определено скалярное произведение.
Обратим внимание на то, что постановка задачи и алгоритм классификации не используют в явном виде признаковое описание и оперируют только скалярными произведениями признаков объектов. Это даёт возможность заменить скалярное произведение в пространстве $X$ на ядро — функцию, являющуюся скалярным произведением в некотором $H$. При этом можно вообще не строить спрямляющее пространство в явном виде, и вместо подбора $\psi$ подбирать непосредственно ядро.
Постановка задачи с применением ядер приобретает вид:
$\begin{cases} -\mathscr{L}(\lambda) = -\sum\limits_{i=1}^\ell \lambda_i + \frac{1}{2} \sum\limits_{i=1}^\ell \sum\limits_{j=1}^\ell \lambda_i \lambda_j y_i y_j \color{brown}{K(\vec{x}_i, \vec{x}_j)} \to \min\limits_\lambda \\ 0 \leq \lambda_i \leq C, \quad i = 1, \ldots, \ell \\ \sum\limits_{i=1}^\ell \lambda_i y_i = 0 \end{cases}$
$a(x) = sign \left(\sum\limits_{i=1}^\ell \lambda_i y_i \color{brown}{K(\vec{x}_i, \vec{x})} - b\right)$
Преимущества и недостатки SVM
Преимущества SVM перед методом стохастического градиента и нейронными сетями:
- Задача выпуклого квадратичного программирования хорошо изучена и имеет единственное решение.
- Метод опорных векторов эквивалентен двухслойной нейронной сети, где число нейронов на скрытом слое определяется автоматически как число опорных векторов.
- Принцип оптимальной разделяющей гиперплоскости приводит к максимизации ширины разделяющей полосы, а следовательно, к более уверенной классификации.
Недостатки классического SVM:
- Неустойчивость к шуму: выбросы в исходных данных становятся опорными объектами-нарушителями и напрямую влияют на построение разделяющей гиперплоскости.
- Не описаны общие методы построения ядер и спрямляющих пространств, наиболее подходящих для конкретной задачи.
- Нет отбора признаков.
- Необходимо подбирать константу $C$ при помощи кросс-валидации.
Модификации
Существуют различные дополнения и модификации метода опорных векторов, направленные на устранение описанных недостатков:
- Метод релевантных векторов (Relevance Vector Machine, RVM)
- 1-norm SVM (LASSO SVM)
- Doubly Regularized SVM (ElasticNet SVM)
- Support Features Machine (SFM)
- Relevance Features Machine (RFM)
Примеры кода
Пример на языке Java
Пример классификации с применением smile.classification.SVM[1]
Maven зависимость:
<dependency> <groupId>com.github.haifengl</groupId> <artifactId>smile-core</artifactId> <version>1.5.2</version> </dependency>
import smile.classification.SVM; import smile.data.NominalAttribute; import smile.data.parser.DelimitedTextParser; import smile.math.kernel.GaussianKernel; import java.util.Arrays;
// read train & test dataset
var parser = new DelimitedTextParser();
parser.setResponseIndex(new NominalAttribute("class"), 0);
var train = parser.parse("USPS Train", this.getClass().getResourceAsStream("/smile/data/usps/zip.train"));
var test = parser.parse("USPS Test", this.getClass().getResourceAsStream("/smile/data/usps/zip.test"));
var classes = Arrays.stream(test.labels()).max().orElse(0) + 1;
// build SVM classifier
var svm = new SVM<>(new GaussianKernel(8.0), 5.0, classes, SVM.Multiclass.ONE_VS_ONE);
svm.learn(train.x(), train.labels());
svm.finish();
// calculate test error rate
var error = 0;
for (int i = 0; i < test.x().length; i++) {
if (svm.predict(test.x()[i]) != test.labels()[i]) {
error++;
}
}
System.out.format("USPS error rate = %.2f%%\n", 100.0 * error / test.x().length);
Пример на языке R
# importing package and its' dependencies
library(caret)
#reading data
data <- read.csv("input.csv", sep = ',', header = FALSE)
# splitting data into train and test sets
index <- createDataPartition(y = data$target, p = 0.8, list = FALSE)
training <- data[index,]
testing <- data[-index,]
# evaluating model
fit <- train(target ~ x + y + z,
data = train_flats,
method = "svmRadial",
trControl = trainControl(method = "repeatedcv", number = 10, repeats = 3))
# printing parameters
print(fit)
См. также
Примечания
Источники информации
- machinelearning.ru — Машина опорных векторов
- Лекция "Линейные методы классификации: метод опорных векторов" — К.В. Воронцов, курс "Машинное обучение" 2014
- Wikipedia — Метод опорных векторов
- Alexey Nefedov — Support Vector Machines: A Simple Tutorial
- John Platt — Sequential Minimal Optimization: A Fast Algorithm for Training Support Vector Machines
- Shai Fine, Katya Scheinberg — INCAS: An Incremental Active Set Method for SVM