Обсуждение:Факторизация графов — различия между версиями
(→Задача о поиске произвольного f-фактора) |
Cczy (обсуждение | вклад) (→Задача о поиске произвольного f-фактора) |
||
| (не показаны 4 промежуточные версии 2 участников) | |||
| Строка 6: | Строка 6: | ||
|definition = Пусть задана функция <tex>f : V(G) \rightarrow \mathbb{N}</tex>, такая что <tex>\forall~v \in V(G):f(v)\leq \text{deg}(v)</tex>. Тогда остовный подграф <tex>G_f</tex> в котором степень каждой вершины <tex>v</tex> равна <tex>f(v)</tex> называется '''<tex>f</tex>-фактором'''. | |definition = Пусть задана функция <tex>f : V(G) \rightarrow \mathbb{N}</tex>, такая что <tex>\forall~v \in V(G):f(v)\leq \text{deg}(v)</tex>. Тогда остовный подграф <tex>G_f</tex> в котором степень каждой вершины <tex>v</tex> равна <tex>f(v)</tex> называется '''<tex>f</tex>-фактором'''. | ||
}} | }} | ||
| + | |||
| + | |||
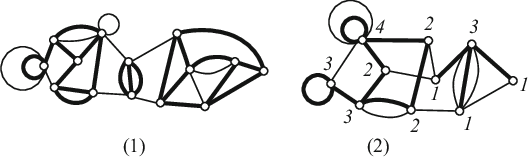
| + | [[Файл:1-A-general-graph-G-with-a-3-regular-factor-2-A-general-graph-G-with-an-f-factor (1).png|700px|thumb|centre| Примеры факторов в графе: (1) {{---}} <tex>3</tex>-фактор, (2) {{---}} <tex>f</tex>-фактор (значения <tex>f(v)</tex> указаны возле вершин)]] | ||
| + | |||
== Задача о поиске произвольного <tex>f</tex>-фактора == | == Задача о поиске произвольного <tex>f</tex>-фактора == | ||
| + | |||
| + | Сведем задачу о поиске <tex>f</tex>-фактора к задаче о поиске наибольшего паросочетания. | ||
Пусть дан граф <tex>G</tex> и функция <tex>f : V(G) \rightarrow \mathbb{N}</tex>. Построим граф <tex>G^*</tex> следующим образом. | Пусть дан граф <tex>G</tex> и функция <tex>f : V(G) \rightarrow \mathbb{N}</tex>. Построим граф <tex>G^*</tex> следующим образом. | ||
| − | # Для каждого ребра <tex>(u,w)\in E(G)</tex> добавим в граф <tex>G^*</tex> | + | # Для каждого ребра <tex>(u,w)\in E(G)</tex> добавим в граф <tex>G^*</tex> по одной новой вершине в множества <tex>S(u)</tex> и <tex>S(w)</tex>, и соединим их ребром <tex>(e(u),e(w))</tex>. В результате каждой вершине <tex>v \in V(G)</tex> будет соответствовать множество <tex>S(v) \subset V(G^*)</tex> такое что <tex>|S(v)|=deg(v)</tex>; Каждому ребру <tex>(u,w) \in E(G)</tex> будет соответствовать ребро <tex>(e(u),e(w))</tex>, причем ни для каких двух ребер из <tex>E(G)</tex> концы соответствующих им ребер в <tex>G^*</tex> не пересекаются. |
# Для каждой вершины <tex>v\in V(G)</tex> добавим в <tex>G^*</tex> новые <tex>deg(v)-f(v)</tex> вершин, образующие множество <tex>T(v)</tex>. Каждую вершину из <tex>T(v)</tex> свяжем ребром с каждой вершиной из <tex>S(v)</tex>. В результате для каждой вершины <tex>v \in V(G)</tex> Множество <tex>S(v)\cup T(v)</tex> образует полный двудольный граф. | # Для каждой вершины <tex>v\in V(G)</tex> добавим в <tex>G^*</tex> новые <tex>deg(v)-f(v)</tex> вершин, образующие множество <tex>T(v)</tex>. Каждую вершину из <tex>T(v)</tex> свяжем ребром с каждой вершиной из <tex>S(v)</tex>. В результате для каждой вершины <tex>v \in V(G)</tex> Множество <tex>S(v)\cup T(v)</tex> образует полный двудольный граф. | ||
| + | |||
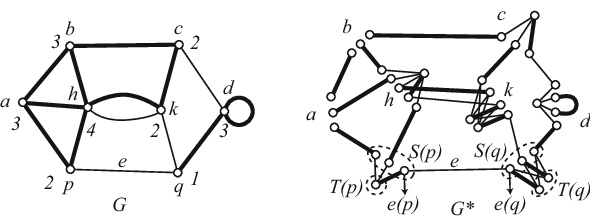
| + | [[Файл:A-general-graph-G-with-an-f-factor-and-the-corresponding-simple-graph-G-with-a.png|700px|thumb|centre| Граф <tex>G</tex> и соответствующий ему граф <tex>G^*</tex>]] | ||
{{Теорема | {{Теорема | ||
|statement = | |statement = | ||
| − | Граф <tex>G</tex> имеет <tex>f</tex>-фактор тогда и только тогда, когда соответствующий | + | Граф <tex>G</tex> имеет <tex>f</tex>-фактор тогда и только тогда, когда соответствующий графу <tex>G</tex> и функции <tex>f</tex> граф <tex>G^*</tex> имеет совершенное паросочетание. |
|proof = | |proof = | ||
<tex>\Rightarrow</tex> | <tex>\Rightarrow</tex> | ||
| Строка 21: | Строка 29: | ||
Пусть граф <tex>G</tex> имеет <tex>f</tex>-фактор <tex>G_f</tex>. Построим паросочетание <tex>M</tex> для графа <tex>G^*</tex> следующим образом: | Пусть граф <tex>G</tex> имеет <tex>f</tex>-фактор <tex>G_f</tex>. Построим паросочетание <tex>M</tex> для графа <tex>G^*</tex> следующим образом: | ||
# Для каждого ребра <tex>(u,w)\in G_f</tex> добавим в <tex>M</tex> соответствующее ему ребро из <tex>G^*</tex> . Теперь для каждой вершины <tex>v \in V(g)</tex> <tex>f(v)</tex> вершин из множества <tex>S(v)</tex> покрыты <tex>M</tex> . | # Для каждого ребра <tex>(u,w)\in G_f</tex> добавим в <tex>M</tex> соответствующее ему ребро из <tex>G^*</tex> . Теперь для каждой вершины <tex>v \in V(g)</tex> <tex>f(v)</tex> вершин из множества <tex>S(v)</tex> покрыты <tex>M</tex> . | ||
| − | # Для каждой вершины <tex>v \in V(g)</tex> пусть <tex>R(v)\subset S(v)</tex> - множество вершин еще не покрытых <tex>M</tex>. <tex>R(v)\cup T(v)</tex> является полным двудольным графом, причем размер каждой из долей равен <tex>deg(v)-f(v)</tex>, следовательно этот граф имеет совершенное паросочетание <tex>M_v</tex>. Добавим каждое ребро из <tex>M_v</tex> в <tex>M</tex>. | + | # Для каждой вершины <tex>v \in V(g)</tex> пусть <tex>R(v)\subset S(v)</tex> {{---}} множество вершин еще не покрытых <tex>M</tex>. <tex>R(v)\cup T(v)</tex> является полным двудольным графом, причем размер каждой из долей равен <tex>deg(v)-f(v)</tex>, следовательно этот граф имеет совершенное паросочетание <tex>M_v</tex>. Добавим каждое ребро из <tex>M_v</tex> в <tex>M</tex>. |
В результате каждая вершина в <tex>G^*</tex> покрыта <tex>M</tex>, следовательно <tex>M</tex> является совершенным паросочетанием. | В результате каждая вершина в <tex>G^*</tex> покрыта <tex>M</tex>, следовательно <tex>M</tex> является совершенным паросочетанием. | ||
| Строка 29: | Строка 37: | ||
}} | }} | ||
| − | Из доказательства напрямую следует, что | + | Из доказательства напрямую следует, что для нахождения <tex>f</tex>-фактора графа <tex>G</tex> достаточно найти совершенное паросочетание в графе <tex>G^*</tex>. Т.к. <tex>G^*</tex> в общем случае не является двудольным, для решения этой задачи можно воспользваться [https://ru.wikipedia.org/wiki/%D0%90%D0%BB%D0%B3%D0%BE%D1%80%D0%B8%D1%82%D0%BC_%D1%81%D0%B6%D0%B0%D1%82%D0%B8%D1%8F_%D1%86%D0%B2%D0%B5%D1%82%D0%BA%D0%BE%D0%B2 Алгоритмом Эдмондса для поиска наибольшего паросочетания]. |
Текущая версия на 21:24, 29 декабря 2019
| Определение: |
| -фактор — регулярный остовный подграф степени . Если граф представляет собой сумму -факторов, то их объединение называется -факторизацией, а сам граф назыается -факторизуемым. |
| Определение: |
| Пусть задана функция , такая что . Тогда остовный подграф в котором степень каждой вершины равна называется -фактором. |
Задача о поиске произвольного -фактора
Сведем задачу о поиске -фактора к задаче о поиске наибольшего паросочетания.
Пусть дан граф и функция . Построим граф следующим образом.
- Для каждого ребра добавим в граф по одной новой вершине в множества и , и соединим их ребром . В результате каждой вершине будет соответствовать множество такое что ; Каждому ребру будет соответствовать ребро , причем ни для каких двух ребер из концы соответствующих им ребер в не пересекаются.
- Для каждой вершины добавим в новые вершин, образующие множество . Каждую вершину из свяжем ребром с каждой вершиной из . В результате для каждой вершины Множество образует полный двудольный граф.
| Теорема: |
Граф имеет -фактор тогда и только тогда, когда соответствующий графу и функции граф имеет совершенное паросочетание. |
| Доказательство: |
|
Пусть граф имеет -фактор . Построим паросочетание для графа следующим образом:
В результате каждая вершина в покрыта , следовательно является совершенным паросочетанием. Пусть имеет совершенное паросочетание . Для каждой вершины является независимым множеством и полностью покрыто , следовательно множество покрыто ребрами, концы которых лежат в , а значит каждая вершина из покрыта ребром, второй конец которого принадлежит , причем . Поэтому если мы добавим в все ребра соответствующие ребрам из покрывающим , то есть все ребра из концы которых лежат в множествах , то степень каждой вершины будет равна , а значит будет являться -фактором. |
Из доказательства напрямую следует, что для нахождения -фактора графа достаточно найти совершенное паросочетание в графе . Т.к. в общем случае не является двудольным, для решения этой задачи можно воспользваться Алгоритмом Эдмондса для поиска наибольшего паросочетания.