Дополнение к ранжированию — различия между версиями
м (→Последовательность) |
м (rollbackEdits.php mass rollback) |
||
| (не показано 10 промежуточных версий 2 участников) | |||
| Строка 1: | Строка 1: | ||
| − | |||
При рассмотрении различных ситуаций, связанных с извлечением экспертных знаний, возникает потребность каким-либо упорядочить все множество оценок, затрагивая уже понятие группового ранжирования. | При рассмотрении различных ситуаций, связанных с извлечением экспертных знаний, возникает потребность каким-либо упорядочить все множество оценок, затрагивая уже понятие группового ранжирования. | ||
| − | Положим, имеется конечное множество | + | Положим, имеется конечное множество <tex>X</tex> объектов (например, экспертных оценок или критериев) и <tex>m</tex> экспертов, пронумерованных индексами <tex>1,2... m</tex>. Каждый <tex>i-</tex>й эксперт выставляет рейтинг, порождая порядок. Подобные тип задач в машинном обучении обозначается как ранжирование. <br \> |
| + | '''Ранжирование''' (англ. ''learning to rank'') {{---}} особый тип задач [[Машинное обучение |машиного обучения ]], связанный с постороением некой ранжирующей модели по обучащей выборке. Отличие от классификации и регрессии состоит в том, что для обучающей выборки не заданы ответы, однако задано [[Отношение порядка |отношение порядка]] для пары объектов. Стоит отметить, что от отношения порядка на множестве объектов изменяется и подход к ранжированию. | ||
| + | |||
== Слабое ранжирование.Представления == | == Слабое ранжирование.Представления == | ||
| Строка 44: | Строка 45: | ||
* '''эквивалентность''': для <tex>a \sim b</tex> ''тогда и только тогда'', когда <tex>u(a)=u(b)</tex>. | * '''эквивалентность''': для <tex>a \sim b</tex> ''тогда и только тогда'', когда <tex>u(a)=u(b)</tex>. | ||
| − | ''Ограничения'': | + | ''Ограничения'': <br \> |
| − | + | Лексикографические предпочтения. Ранжирующая функция может быть определена на любом конечном множестве, однако для случая лексикографического порядка функция не определена на <tex>R^n</tex>. <br \> | |
| − | + | [[Отображения |Инъективность]]. В случае, если бы <tex>u</tex> являлась бы инъективной функцией, то класс эквивалентности двух элементов множества <tex>Y</tex> мог бы переходить в более широкий соответствующий класс на множестве <tex>X</tex>. <br \> | |
| − | + | [[Отображения |Сюрьективность]]. Если на <tex>u</tex> вводятся ограничения, чтобы быть сюръективной функцией, то при отображении элементов некого класса на <tex>Y</tex> возможно соответствие ему меньшего или вовсе пустого класса на <tex>X</tex>. | |
| − | |||
| − | |||
| − | |||
====== Кусочная последовательность ====== | ====== Кусочная последовательность ====== | ||
| Строка 81: | Строка 79: | ||
''Ограничения'': | ''Ограничения'': | ||
| + | |||
Если у данного частичного ранжирования существует несчетное множество строго упорядоченных объектов, то невозможно подобрать такую <tex>u</tex>. В противовес, любое конечное частичное ранжирование может быть описано с помощью <tex>u</tex>. | Если у данного частичного ранжирования существует несчетное множество строго упорядоченных объектов, то невозможно подобрать такую <tex>u</tex>. В противовес, любое конечное частичное ранжирование может быть описано с помощью <tex>u</tex>. | ||
| Строка 111: | Строка 110: | ||
== Supervised алгоритмы ранжирования == | == Supervised алгоритмы ранжирования == | ||
=== OC-SVM === | === OC-SVM === | ||
| − | Ordinal Classification SVM - алгоритм поточечного ранжирования, рассматривающий каждый объект обособленно. В основе стоит использования идеи [[Метод опорных векторов (SVM) |метода опорных векторов]] о проведении разделяющей гиперплоскости над множеством оценок. | + | Ordinal Classification SVM {{---}} алгоритм поточечного ранжирования, рассматривающий каждый объект обособленно. В основе стоит использования идеи [[Метод опорных векторов (SVM) |метода опорных векторов]] о проведении разделяющей гиперплоскости над множеством оценок. |
==== Постановка задачи ==== | ==== Постановка задачи ==== | ||
Пусть имеется некое число градаций (оценок, предпочтений) <tex>K</tex>, тогда <tex>Y=\{1,2 ...K\}</tex> {{---}} ранжирующая функция с порогами <center> <tex>b_0=-\infty</tex>, <tex>b_1,b_2 ...b_{K-1} \in R, b_k=\infty:</tex></center> | Пусть имеется некое число градаций (оценок, предпочтений) <tex>K</tex>, тогда <tex>Y=\{1,2 ...K\}</tex> {{---}} ранжирующая функция с порогами <center> <tex>b_0=-\infty</tex>, <tex>b_1,b_2 ...b_{K-1} \in R, b_k=\infty:</tex></center> | ||
<center><tex>a(x)=y</tex>, если <tex>b_{y-1}<(w,x)\le b_y </tex> </center> | <center><tex>a(x)=y</tex>, если <tex>b_{y-1}<(w,x)\le b_y </tex> </center> | ||
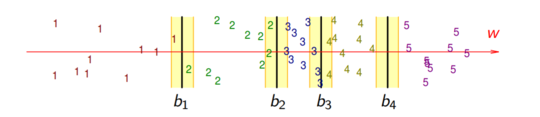
| − | Основное отличие от классического подхода в том, что на имеющееся <tex>K</tex> границ необходимо найти <tex>K-1</tex> зазоров. Иными словами, необходимо '''найти один направляющий вектор''' <tex>K-1</tex> числа гиперплоскостей. Исходим от предположения, что найдется такое направление, в котором объекты удовлетворительно отранжировались. Пример такого разделения для <tex>K=5</tex> представлен на [[Медиа:OC-svm.PNG| | + | Основное отличие от классического подхода в том, что на имеющееся <tex>K</tex> границ необходимо найти <tex>K-1</tex> зазоров. Иными словами, необходимо '''найти один направляющий вектор''' <tex>K-1</tex> числа гиперплоскостей. Исходим от предположения, что найдется такое направление, в котором объекты удовлетворительно отранжировались. Пример такого разделения для <tex>K=5</tex> представлен на [[Медиа:OC-svm.PNG|рисунке 1]]. |
{|align="center" | {|align="center" | ||
|-valign="top" | |-valign="top" | ||
| Строка 159: | Строка 158: | ||
Воспользовавшись методом стохастического градиентного спуска, выбираем на каждой <tex>i-</tex>ой итерации случайным образом запрос <tex>q \in Q</tex> и пару документов из запроса <tex> i\prec j </tex>, получаем итеративную формулу вычисления весов: | Воспользовавшись методом стохастического градиентного спуска, выбираем на каждой <tex>i-</tex>ой итерации случайным образом запрос <tex>q \in Q</tex> и пару документов из запроса <tex> i\prec j </tex>, получаем итеративную формулу вычисления весов: | ||
<center><tex> w = w + \eta \frac{\sigma }{1 + e(\sigma \langle x_j - x_i,w\rangle)}\cdot (x_j - x_i) </tex></center> | <center><tex> w = w + \eta \frac{\sigma }{1 + e(\sigma \langle x_j - x_i,w\rangle)}\cdot (x_j - x_i) </tex></center> | ||
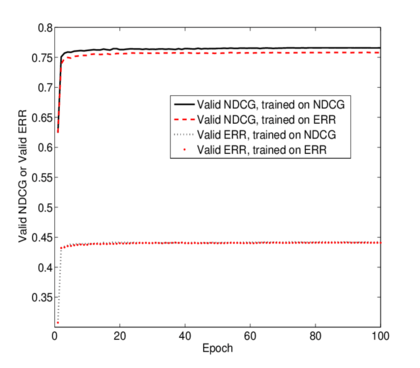
| − | Чтобы перейти к использованию негладких функционалов MAP, NDCD, pFound необходимо домножить <tex>1 + e(\sigma \langle x_j - x_i,w\rangle)</tex> на изменение данного функционала при перестановке местами <tex>x_i</tex> и <tex>x_j</tex> в каждой итерации. Это означает, как изменится веса модели, если в задаче ранжирования поменять местами два документа. Результаты оценки алгоритма с разным функционалом представлены на [[Медиа:LambdaRank.png| | + | Чтобы перейти к использованию негладких функционалов MAP, NDCD, pFound необходимо домножить <tex>1 + e(\sigma \langle x_j - x_i,w\rangle)</tex> на изменение данного функционала при перестановке местами <tex>x_i</tex> и <tex>x_j</tex> в каждой итерации. Это означает, как изменится веса модели, если в задаче ранжирования поменять местами два документа. Результаты оценки алгоритма с разным функционалом представлены на [[Медиа:LambdaRank.png|рисунке 2]]. |
'''LambdaRank''' моделирует следующий итеративный процесс: | '''LambdaRank''' моделирует следующий итеративный процесс: | ||
| Строка 169: | Строка 168: | ||
'''SoftRank''' {{---}} списочный метод ранжирования, который предполагает использовать ''сглаживание''<ref>[https://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.469.3608&rep=rep1&type=pdf SoftRank: Optimizing Non-Smooth Rank Metrics]</ref> для возможности диффиренцирования значения сложной метрики. | '''SoftRank''' {{---}} списочный метод ранжирования, который предполагает использовать ''сглаживание''<ref>[https://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.469.3608&rep=rep1&type=pdf SoftRank: Optimizing Non-Smooth Rank Metrics]</ref> для возможности диффиренцирования значения сложной метрики. | ||
==== Постановка задачи ==== | ==== Постановка задачи ==== | ||
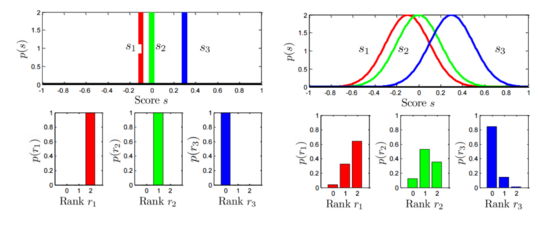
| − | Сперва необходимо перейти от поиска изначально детерминированного положения документа в отранижрованном порядке к случайной величине, распределенной по нормальному закону так, чтобы центр распределения лежал в предсказании функции ранжирования, как представлено на [[Медиа:SoftRank_F.png| | + | Сперва необходимо перейти от поиска изначально детерминированного положения документа в отранижрованном порядке к случайной величине, распределенной по нормальному закону так, чтобы центр распределения лежал в предсказании функции ранжирования, как представлено на [[Медиа:SoftRank_F.png|рисунке 3]]. Величина дисперсии теперь также параметр модели: |
<center><tex> p(d_i)=\mathbb{N}(d_i|\overline{d_i}\cdot \sigma^2_{d_i}) = \mathbb{N}(d_i |a(w,x_i),\cdot \sigma^2_{d_i})</tex></center> | <center><tex> p(d_i)=\mathbb{N}(d_i|\overline{d_i}\cdot \sigma^2_{d_i}) = \mathbb{N}(d_i |a(w,x_i),\cdot \sigma^2_{d_i})</tex></center> | ||
{|align="center" | {|align="center" | ||
| Строка 190: | Строка 189: | ||
<tex> p_j^3(1)=p_j^2(0)\cdot \pi_{2,j} + p_j^{i-1}(1)\cdot (1- \pi_{2,j}) </tex> <br /> | <tex> p_j^3(1)=p_j^2(0)\cdot \pi_{2,j} + p_j^{i-1}(1)\cdot (1- \pi_{2,j}) </tex> <br /> | ||
и т.д. <br /> | и т.д. <br /> | ||
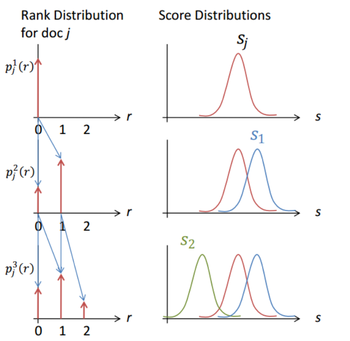
| − | Графическая интерпритация вычислительного процесса представлена на [[Медиа:SR_pr.png| | + | Графическая интерпритация вычислительного процесса представлена на [[Медиа:SR_pr.png|рисунке 4.]] |
Текущая версия на 19:26, 4 сентября 2022
При рассмотрении различных ситуаций, связанных с извлечением экспертных знаний, возникает потребность каким-либо упорядочить все множество оценок, затрагивая уже понятие группового ранжирования.
Положим, имеется конечное множество объектов (например, экспертных оценок или критериев) и экспертов, пронумерованных индексами . Каждый й эксперт выставляет рейтинг, порождая порядок. Подобные тип задач в машинном обучении обозначается как ранжирование.
Ранжирование (англ. learning to rank) — особый тип задач машиного обучения , связанный с постороением некой ранжирующей модели по обучащей выборке. Отличие от классификации и регрессии состоит в том, что для обучающей выборки не заданы ответы, однако задано отношение порядка для пары объектов. Стоит отметить, что от отношения порядка на множестве объектов изменяется и подход к ранжированию.
Содержание
Слабое ранжирование.Представления
Строгое слабое упорядовачивание
| Определение: |
Бинарное отношение на множестве , которое является частично упорядоченным, называется слабым упорядочиванием (англ. weak ordering), если оно обладает следующими свойствами:
|
Рассмотрим случаи, определеяющее частичное упорядочение как:
- Сильное: и , то есть если ~ .
- Слабое[1]: если , то и .
Можно заключить, что любое cильное упорядовачивание есть слабое. Отношение несравнимости является отношением эквивалентности для всех своих разбиений на множестве , что являются линейно упорядоченными.
Сильный подпорядок
| Определение: |
| Сильный подпорядок — такой подпорядок, на котором присутствует отношение связанности. |
Сильный подпорядок обладает рядом следующих свойств:
- Транзитивность: если и .
- Связанности: выполнимо либо , либо .
Если в любом сильном подпорядке и , то на нем определено отношение эквивалентности. Поскольку операция определена для всех элементов, такие подпорядки еще называют отношением предпочтения[2].
Сравнения
Вещественная функция
Удобство использования слабого ранжирования в том, что его элементы могут быть представлены единственным образом с помощью вещественных функций. Рассмотрим следующую теорему.
| Теорема: |
Для любого частичного упорядочивания слабое тогда и только тогда, когда существует и отображение если , то и наоборот. |
Таким образом, чтобы имели место быть:
- частичный подпорядок: для тогда и только тогда, когда .
- эквивалентность: для тогда и только тогда, когда .
Ограничения:
Лексикографические предпочтения. Ранжирующая функция может быть определена на любом конечном множестве, однако для случая лексикографического порядка функция не определена на .
Инъективность. В случае, если бы являлась бы инъективной функцией, то класс эквивалентности двух элементов множества мог бы переходить в более широкий соответствующий класс на множестве .
Сюрьективность. Если на вводятся ограничения, чтобы быть сюръективной функцией, то при отображении элементов некого класса на возможно соответствие ему меньшего или вовсе пустого класса на .
Кусочная последовательность
Для любого конечного множества , на котором задано отношение слабого упорядовачивания и , может быть применимо моделирование с помощью кусочных последовательностей. Рассмотрим пример. Положим, что
Тогда слабое ранжирование представляется в виде следующего:
Частичное ранжирование
| Определение: |
Бинарное отношение на множестве , для некоторых элементов которого определена несравнимость ,называется частичным упорядочиванием (англ. semiorder), если оно обладает следующими свойствами:
|
Сравнения
Вещественная функция
Частичное ранжирование поддается тому же функциональному подходу к сравнению за тем лишь исключением, что для численных значений объектов вводится некоторая погрешность , внутри которой объекты считаются сравнимы, снаружи - нет. Зачастую такую погрешность выбирают нормированной к .
| Теорема: |
Для любого конечного частичного упорядочиванием возможно определить такое и функционал если , то и наоборот. |
Интервальный метод
Имея заданный функционал и возможно использование интервального сравнения, а именно — объекты считаются сравнимы, если значения их оценок лежат в некотором интервале. Так, например, если , то .
Ограничения:
Если у данного частичного ранжирования существует несчетное множество строго упорядоченных объектов, то невозможно подобрать такую . В противовес, любое конечное частичное ранжирование может быть описано с помощью .
Сильное ранжирование
| Определение: |
Бинарное отношение на множестве , для некоторых элементов которого определена несравнимость ,называется сильным ранжированием (англ. total order), если оно обладает следующими свойствами:
|
Таким образом, сильное ранжирование — строгое слабое, для которого .
Сравнения
Вещественная функция
Сильное ранжирование сравнивается с помощью функционала .
| Лемма: |
Для любого конечного сильного упорядочивания возможно определить такой функционал если , то и наоборот. |
Последовательность
Для любого конечного множества , на котором задано отношение сильного упорядочивания и , может быть применимо моделирование с помощью порождения последовательности значений элементов. Иными словами, задается новый функционал , что все оценки образуют последовательность.
Ограничения:
Как и для частичного, множество должно быть конечно.
Supervised алгоритмы ранжирования
OC-SVM
Ordinal Classification SVM — алгоритм поточечного ранжирования, рассматривающий каждый объект обособленно. В основе стоит использования идеи метода опорных векторов о проведении разделяющей гиперплоскости над множеством оценок.
Постановка задачи
Пусть имеется некое число градаций (оценок, предпочтений) , тогда — ранжирующая функция с порогамиОсновное отличие от классического подхода в том, что на имеющееся границ необходимо найти зазоров. Иными словами, необходимо найти один направляющий вектор числа гиперплоскостей. Исходим от предположения, что найдется такое направление, в котором объекты удовлетворительно отранжировались. Пример такого разделения для представлен на рисунке 1.
Подход
Поскольку теперь увеличилось число зазоров, классического значения штрафа недостаточно — необходимы штрафы и для нарушение с левой и правой сторон соответственно ой границы. Ограничительное условие для такого случая состоит в том, что произвольный объект , оказавшийся между разделяющими полосами, не должен выйти за их пределы ни слева, ни справа, что можно записать как:
Для случая крайних границ, для объектов может существовать только нарушение слева от границы, когда для объектов — только справа от границы. Таким образом, задача может быть сформирована как задача минимизации с ограничениями:
Ranking SVM
Алгоритм для попарного подхода[3] к ранжированию. Основное отличие от алгоритма SVM в том, что теперь объекты нумеруются попарно.
Постановка задачи
Считаем, что теперь решаем следующую оптимизационную задачу:
Подход
Поскольку теперь все операции выполяняются уже для пары объектов, то строгая система ограничений будет отличаться в соответствующих местах:
RankNet, LambdaRank
Данные алгоритмы применяются для списочного ранжирования, хотя по сути своей используют попарный подход, который был расширен до случая списка.
Постановка задачи
Считаем, что у нас есть некий гладкий функционал качества, который необходимо оптимизировать:
Конкретную функцию потерь в оригинальной работе[4] выбирают как логистическую функцию потерь, те
масштабирующий параметр для пересчета значения отступа в вероятностное значение.
Подход
Воспользовавшись методом стохастического градиентного спуска, выбираем на каждой ой итерации случайным образом запрос и пару документов из запроса , получаем итеративную формулу вычисления весов:
Чтобы перейти к использованию негладких функционалов MAP, NDCD, pFound необходимо домножить на изменение данного функционала при перестановке местами и в каждой итерации. Это означает, как изменится веса модели, если в задаче ранжирования поменять местами два документа. Результаты оценки алгоритма с разным функционалом представлены на рисунке 2.
LambdaRank моделирует следующий итеративный процесс:
Оптмизируется тем самым по функционалу NDCD.
SoftRank
SoftRank — списочный метод ранжирования, который предполагает использовать сглаживание[5] для возможности диффиренцирования значения сложной метрики.
Постановка задачи
Сперва необходимо перейти от поиска изначально детерминированного положения документа в отранижрованном порядке к случайной величине, распределенной по нормальному закону так, чтобы центр распределения лежал в предсказании функции ранжирования, как представлено на рисунке 3. Величина дисперсии теперь также параметр модели:
Возможно оценить вероятность того, что некий документ й окажется выше го.
Теперь задача формулируется следующим образом: оценить вероятность того, что й документ окажется на позиции .
Подход
Вычисления происходят рекурсивно для каждого го документа.
. Оценить вероятность оказаться на м месте для элемента:
. Тогда вероятность оказаться на м и м месте для двух документов:
. Для выборки из х элементов, вероятность оказаться на первом месте:
и т.д.
Графическая интерпритация вычислительного процесса представлена на рисунке 4.
Чтобы использовать метрику NDCG необходимо учесть математическое ожидание ассесорской оценки , что уже дает гладкий функционал:
Данное выражения уже возможно оптимизировать градиентом:
вычислятся через :