Равномерная сходимость функционального ряда — различия между версиями
(Добавлена статья) |
м (rollbackEdits.php mass rollback) |
||
| (не показаны 24 промежуточные версии 10 участников) | |||
| Строка 1: | Строка 1: | ||
| + | [[Определение функционального ряда|<<]] [[Операции анализа с функциональными рядами|>>]] | ||
== Поточечная сходимость == | == Поточечная сходимость == | ||
То, как была определена сумма функционального ряда, не учитывает то, что функция {{---}} закон | То, как была определена сумма функционального ряда, не учитывает то, что функция {{---}} закон | ||
| Строка 4: | Строка 5: | ||
изолированно. | изолированно. | ||
| − | Пусть на <tex>E</tex> <tex>f_n</tex> обладает свойством <tex>P</tex>(например, непрерывность на <tex>E</tex>). И пусть <tex>\ | + | Пусть на <tex>E</tex> <tex>f_n</tex> обладает свойством <tex>P</tex>(например, непрерывность на <tex>E</tex>). И пусть для любого <tex> x \in E </tex> есть предел соответствующей числовой последовательности. Возникает вопрос: "Будет ли <tex>f = \lim\limits_{n \rightarrow \infty} f_n</tex> обладать свойством <tex>P</tex>?" |
| − | |||
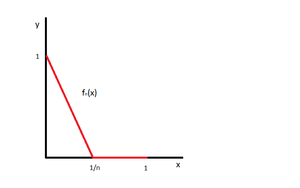
| − | Приведем пример, показывающий, что если требовать лишь поточечной сходимости, то для <tex> | + | Приведем пример, показывающий, что если требовать лишь поточечной сходимости, то для <tex> f </tex> |
свойство <tex>P</tex> может отсутствовать. | свойство <tex>P</tex> может отсутствовать. | ||
| Строка 14: | Строка 14: | ||
0, & x \in (\frac1n; 1]\\ | 0, & x \in (\frac1n; 1]\\ | ||
\end{cases}</tex> | \end{cases}</tex> | ||
| + | |||
| + | [[file:picture1.png|300px]] | ||
Все <tex>f_n</tex> непрерывны на <tex>[0; 1]</tex>. <tex>f_n(0) = 1 \to 1</tex>, <tex>f(0) = 1</tex>. | Все <tex>f_n</tex> непрерывны на <tex>[0; 1]</tex>. <tex>f_n(0) = 1 \to 1</tex>, <tex>f(0) = 1</tex>. | ||
| Строка 30: | Строка 32: | ||
|definition= | |definition= | ||
<tex>f_1, f_2, \ldots</tex> равномерно сходится к <tex>f(x)</tex>, если | <tex>f_1, f_2, \ldots</tex> равномерно сходится к <tex>f(x)</tex>, если | ||
| − | <tex>\forall \varepsilon\ \exists N\ \forall n > N\ \forall x \in E : |f_n(x) - f(x)| < \varepsilon</tex> | + | <tex>\forall \varepsilon\ > 0\ \exists N\ \forall n > N\ \forall x \in E : |f_n(x) - f(x)| < \varepsilon</tex> |
Пишут, что <tex>f_n \rightrightarrows f</tex>. | Пишут, что <tex>f_n \rightrightarrows f</tex>. | ||
}} | }} | ||
| Строка 38: | Строка 40: | ||
Пусть на <tex>E</tex> задан функциональный ряд <tex>\sum\limits_{n = 1}^\infty f_n</tex>. Тогда он равномерно сходится к | Пусть на <tex>E</tex> задан функциональный ряд <tex>\sum\limits_{n = 1}^\infty f_n</tex>. Тогда он равномерно сходится к | ||
<tex>f = \sum f_n</tex>, если | <tex>f = \sum f_n</tex>, если | ||
| − | <tex>\forall\varepsilon\ \exists N\ \forall n > N\ \forall x \in E : | | + | <tex>\forall\varepsilon\ > 0\ \exists N\ \forall n > N\ \forall x \in E : |S_n(x) - f(x)| < \varepsilon</tex> |
}} | }} | ||
| − | Далее всё будем писать на языке функциональных рядов, так как | + | Далее всё будем писать на языке функциональных рядов, так как их наиболее удобно использовать в |
| − | математическом анализе. | + | математическом анализе, и вообще это очень круто и популярно. |
== Критерий Коши равномерной сходимости == | == Критерий Коши равномерной сходимости == | ||
| Строка 48: | Строка 50: | ||
{{Теорема | {{Теорема | ||
|about=Критерий Коши равномерной сходимости | |about=Критерий Коши равномерной сходимости | ||
| − | |statement=Ряд равномерно сходится на <tex>E</tex> <tex>\iff</tex> <tex>\forall\varepsilon\ \exists N\ \forall m \geq n > N\ \forall x \in E : \left|\sum\limits_{k = n}^m f_k(x)\right| < \varepsilon</tex> | + | |statement=Ряд равномерно сходится на <tex>E</tex> <tex>\iff</tex> <tex>\forall\varepsilon\ > 0\ \exists N\ \forall m, n : m \geq n > N\ \forall x \in E : \left|\sum\limits_{k = n}^m f_k(x)\right| < \varepsilon</tex> |
|proof= | |proof= | ||
<tex>\Longrightarrow</tex> Пусть ряд равномерно сходится. | <tex>\Longrightarrow</tex> Пусть ряд равномерно сходится. | ||
| − | <tex>\sum\limits_{k = n}^m f_k = | + | <tex>\sum\limits_{k = n}^m f_k = S_m - S_{n - 1}</tex> |
| − | <tex>\left|\sum\limits_{k = n}^m \right| = |( | + | <tex>\left|\sum\limits_{k = n}^m f_k \right| = |(S_m - S) + (S - S_{n - 1})|</tex>, где <tex>S</tex> {{---}} сумма ряда. Тогда |
| − | <tex>\left|\sum\limits_{k = n}^m f_k(x)\right| \leq | | + | <tex>\left|\sum\limits_{k = n}^m f_k(x)\right| \leq |S_m - S| + |S_{n - 1} - S|</tex> |
| − | По определению равномерной сходимости, <tex>\forall \varepsilon\ \exists N\ \forall p > N\ \forall x \in E : | | + | По определению равномерной сходимости, <tex>\forall \varepsilon\ \exists N\ \forall p > N\ \forall x \in E : |S_p(x) - S(x)| < \varepsilon</tex>. |
| − | <tex>m,n - 1 | + | <tex>m, n - 1 > N </tex> |
В силу предыдущего неравенства, <tex>\forall x \in E : \left|\sum\limits_{k = n}^m f_k(x)\right| \leq 2\varepsilon</tex>, то есть, | В силу предыдущего неравенства, <tex>\forall x \in E : \left|\sum\limits_{k = n}^m f_k(x)\right| \leq 2\varepsilon</tex>, то есть, | ||
| Строка 67: | Строка 69: | ||
<tex>\Longleftarrow</tex> Пусть выполняется условие критерия Коши. | <tex>\Longleftarrow</tex> Пусть выполняется условие критерия Коши. | ||
| − | <tex>\forall x \in E</tex> для <tex>\sum\limits_{n = 1}^\infty f_n(x)</tex> выполняется критерий Коши | + | |
| + | <tex>\forall x \in E</tex> для <tex>\sum\limits_{n = 1}^\infty f_n(x)</tex> выполняется критерий Коши сходимости числовых рядов. | ||
Значит, этот ряд сходится. На всем <tex>E</tex> определена его сумма. Осталось установить равномерную сходимость ряда. | Значит, этот ряд сходится. На всем <tex>E</tex> определена его сумма. Осталось установить равномерную сходимость ряда. | ||
| Строка 73: | Строка 76: | ||
Как и в первой половине доказательства, | Как и в первой половине доказательства, | ||
| − | <tex>| | + | <tex>|S_m(x) - S_{n - 1}(x)| \leq \varepsilon</tex>, но <tex>S_p(x) \to S(x)</tex>. В неравенстве с <tex>\varepsilon</tex> |
| − | можно подставлять любой фиксированный <tex>x</tex>. Устремим <tex> | + | можно подставлять любой фиксированный <tex>x</tex>. Устремим <tex>m \to \infty</tex>: <tex>\forall n > N\ \forall x \in E : |S_n(x) - S(x)| \leq \varepsilon</tex> |
Значит, определение равномерной сходимости проверено. | Значит, определение равномерной сходимости проверено. | ||
| Строка 81: | Строка 84: | ||
== Признак Вейерштрасса == | == Признак Вейерштрасса == | ||
| − | Существует простой признак для проверки равномерной сходимости( | + | Существует простой признак для проверки равномерной сходимости (признак Вейерштрасса) |
| − | |||
| − | |||
Можно рассматривать <tex>\sum\limits_{n = 1}^\infty |f_n|</tex> и при этом сохраняется терминология числовых рядов, | Можно рассматривать <tex>\sum\limits_{n = 1}^\infty |f_n|</tex> и при этом сохраняется терминология числовых рядов, | ||
связанная с абсолютной и условной сходимостью. | связанная с абсолютной и условной сходимостью. | ||
| − | |||
Как и в рядах, абсолютная сходимость сильнее сходимости: из абсолютной сходимости вытекает сходимость. | Как и в рядах, абсолютная сходимость сильнее сходимости: из абсолютной сходимости вытекает сходимость. | ||
| − | {{ | + | {{Теорема |
|author=Вейерштрасс | |author=Вейерштрасс | ||
|statement= | |statement= | ||
| − | <tex>\sum\limits_{n = 1}^\infty f_n</tex>, <tex>\forall x \in E : |f_n(x)| \leq a_n</tex>, <tex>\sum\limits_{n = 1}^\infty a_n</tex> {{---}} сходится. | + | <tex>\sum\limits_{n = 1}^\infty f_n</tex>, <tex>\forall n \in \mathbb{N} </tex> , <tex> \forall x \in E : |f_n(x)| \leq a_n</tex>, <tex>\sum\limits_{n = 1}^\infty a_n</tex> {{---}} сходится. |
Тогда <tex>\sum\limits_{n = 1}^\infty f_n</tex> равномерно сходится на <tex>E</tex>. | Тогда <tex>\sum\limits_{n = 1}^\infty f_n</tex> равномерно сходится на <tex>E</tex>. | ||
|proof= | |proof= | ||
| Строка 101: | Строка 101: | ||
<tex>\left|\sum\limits_{k = n}^m f_k(x) \right|</tex> <tex>\leq \sum\limits_{k = n}^m |f_k(x)|</tex> <tex>\leq \sum\limits_{k = n}^m a_k</tex> | <tex>\left|\sum\limits_{k = n}^m f_k(x) \right|</tex> <tex>\leq \sum\limits_{k = n}^m |f_k(x)|</tex> <tex>\leq \sum\limits_{k = n}^m a_k</tex> | ||
| − | <tex>\sum\limits_{k = n}^m a_k < +\infty \Rightarrow \forall\varepsilon\ \exists N\ \forall m \geq n > N : \sum\limits_{k = n}^m a_k < \varepsilon</tex> | + | <tex>\sum\limits_{k = n}^m a_k < +\infty \Rightarrow \forall\varepsilon\ > 0\ \exists N\ \forall m \geq n > N : \sum\limits_{k = n}^m a_k < \varepsilon</tex> |
Сопоставляя с предыдущим неравенством, которое верно <tex>\forall x</tex>, | Сопоставляя с предыдущим неравенством, которое верно <tex>\forall x</tex>, | ||
| − | <tex>\left|\sum\limits_{k = n}^m f_k(x)\right| | + | <tex>\left|\sum\limits_{k = n}^m f_k(x)\right| < \varepsilon</tex>. Тогда, по критерию Коши, ряд равномерно сходится. |
| + | }} | ||
| + | == Признак Абеля-Дирихле == | ||
| + | {{Теорема | ||
| + | |author=Абель-Дирихле | ||
| + | |statement=Для равномерной сходимости на множестве <tex>E</tex> ряда <tex>\sum\limits_{n = 1}^\infty a_n(x) b_n(x)</tex> , <tex> a_n:E \to \mathbb C</tex> и <tex> b_n:E \to \mathbb R</tex> достаточно, чтобы выполнялась пара условий <tex> \forall x \in E </tex>: | ||
| + | |||
| + | 1)Частичные суммы <tex> S_k(x)= \sum\limits_{n = 1}^k a_n(x) </tex> ряда <tex>\sum\limits_{n = 1}^\infty a_n(x) </tex> равномерно ограничены на <tex>E</tex>; | ||
| + | |||
| + | 2)Последовательность функций <tex>b_n(x)</tex> монотонна и равномерно сходится к нулю на <tex>E</tex>. | ||
| + | |||
| + | |proof= | ||
| + | |||
| + | Монотонность последовательности <tex>b_n(x)</tex> позволяет при каждом <tex>x \in E</tex> записать оценку: | ||
| + | |||
| + | <tex> |\sum\limits_{k = n}^m a_k(x) b_k(x)| \leq 4 max |A_k(x)| * max( |b_n(x)|, |b_m(x)| )</tex> | ||
| + | |||
| + | где <tex> n - 1 \leq k \leq m </tex> и в качестве <tex> A_k(x)</tex> возьмем <tex> S_k(x) - S_{n-1}(x) </tex> . | ||
| + | |||
| + | Если выполнена пара условий 1) и 2), то с одной стороны существует такая постоянная <tex>M</tex>,что <tex>|A_k(x)| \leq M</tex> при любом <tex> k \in N </tex> и любом <tex>x \in E</tex>, а с другой стороны, какого бы ни было число <tex>\varepsilon > 0 </tex>, при всех достаточно больших значениях <tex>m</tex> и <tex>n</tex> и любом <tex> x\in E</tex> будет выполнено неравенство <tex> max( |b_n(x)|, |b_m(x)| ) < \frac{\varepsilon}{4M} </tex>. Значит, что при всех достаточно больших значениях <tex>m</tex> и <tex>n</tex> и любом <tex> x \in E </tex> будет <tex>|\sum\limits_{k = n}^m a_k(x) b_k(x)| < \varepsilon </tex>, т.е. для рассматриваемого ряда выполнен критерий Коши равномерной сходимости. | ||
}} | }} | ||
| + | |||
| + | [[Определение функционального ряда|<<]] [[Операции анализа с функциональными рядами|>>]] | ||
| + | [[Категория:Математический анализ 1 курс]] | ||
Текущая версия на 19:07, 4 сентября 2022
Содержание
Поточечная сходимость
То, как была определена сумма функционального ряда, не учитывает то, что функция — закон соответствия, который каждому сопоставляет некоторое число. При этом, все фигурировали изолированно.
Пусть на обладает свойством (например, непрерывность на ). И пусть для любого есть предел соответствующей числовой последовательности. Возникает вопрос: "Будет ли обладать свойством ?"
Приведем пример, показывающий, что если требовать лишь поточечной сходимости, то для свойство может отсутствовать.
Все непрерывны на . , .
: . Тогда, начиная с некоторого , все
Тогда будет разрывна в нуле, свойство непрерывности не сохранилось.
Равномерная сходимость
Возникает вопрос: "Что ещё надо потребовать от поточечной сходимости, чтобы в пределе сохранилось?"
Классическое требование: равномерная сходимость.
| Определение: |
| равномерно сходится к , если
Пишут, что . |
| Определение: |
| Пусть на задан функциональный ряд . Тогда он равномерно сходится к
, если |
Далее всё будем писать на языке функциональных рядов, так как их наиболее удобно использовать в
математическом анализе, и вообще это очень круто и популярно.
Критерий Коши равномерной сходимости
| Теорема (Критерий Коши равномерной сходимости): |
Ряд равномерно сходится на |
| Доказательство: |
|
Пусть ряд равномерно сходится.
, где — сумма ряда. Тогда
По определению равномерной сходимости, .
В силу предыдущего неравенства, , то есть, выполняется условие критерия Коши.
для выполняется критерий Коши сходимости числовых рядов. Значит, этот ряд сходится. На всем определена его сумма. Осталось установить равномерную сходимость ряда. По условию критерия Коши, Как и в первой половине доказательства, , но . В неравенстве с можно подставлять любой фиксированный . Устремим : Значит, определение равномерной сходимости проверено. |
Признак Вейерштрасса
Существует простой признак для проверки равномерной сходимости (признак Вейерштрасса)
Можно рассматривать и при этом сохраняется терминология числовых рядов, связанная с абсолютной и условной сходимостью.
Как и в рядах, абсолютная сходимость сильнее сходимости: из абсолютной сходимости вытекает сходимость.
| Теорема (Вейерштрасс): |
, , , — сходится.
Тогда равномерно сходится на . |
| Доказательство: |
|
Применим критерий Коши:
Сопоставляя с предыдущим неравенством, которое верно , . Тогда, по критерию Коши, ряд равномерно сходится. |
Признак Абеля-Дирихле
| Теорема (Абель-Дирихле): |
Для равномерной сходимости на множестве ряда , и достаточно, чтобы выполнялась пара условий :
1)Частичные суммы ряда равномерно ограничены на ; 2)Последовательность функций монотонна и равномерно сходится к нулю на . |
| Доказательство: |
|
Монотонность последовательности позволяет при каждом записать оценку:
где и в качестве возьмем . Если выполнена пара условий 1) и 2), то с одной стороны существует такая постоянная ,что при любом и любом , а с другой стороны, какого бы ни было число , при всех достаточно больших значениях и и любом будет выполнено неравенство . Значит, что при всех достаточно больших значениях и и любом будет , т.е. для рассматриваемого ряда выполнен критерий Коши равномерной сходимости. |