Проблемы нейронных сетей — различия между версиями
Garuda-1 (обсуждение | вклад) (Внесение второго набора правок) |
м (rollbackEdits.php mass rollback) |
| (не показана 1 промежуточная версия 1 участника) | |
(нет различий)
| |
Текущая версия на 19:08, 4 сентября 2022
Нейронные сети считаются универсальными моделями в машинном обучении, поскольку позволяют решать широкий класс задач. Однако, при их использовании могут возникать различные проблемы.
Содержание
Взрывающийся и затухающий градиент
Определение
Напомним, что градиентом в нейронных сетях называется вектор частных производных функции потерь по весам нейронной сети. Таким образом, он указывает на направление наибольшего роста этой функции для всех весов по совокупности. Градиент считается в процессе тренировки нейронной сети и используется в оптимизаторе весов для улучшения качества модели.
В процессе обратного распространения ошибки при прохождении через слои нейронной сети в элементах градиента могут накапливаться большие значения, что будет приводить к сильным изменениям весов. Это в свою очередь может сделать нестабильным алгоритм обучения нейронной сети. В таком случае элементы градиента могут переполнить тип данных, в котором они хранятся. Такое явление называется взрывающимся градиентом (англ. exploding gradient).
Существует аналогичная обратная проблема, когда в процессе обучения при обратном распространении ошибки через слои нейронной сети градиент становится все меньше. Это приводит к тому, что веса при обновлении изменяются на слишком малые значения, и обучение проходит неэффективно или останавливается, то есть алгоритм обучения не сходится. Это явление называется затухающим градиентом (англ. vanishing gradient).
Таким образом, увеличение числа слоев нейронной сети с одной стороны увеличивает ее способности к обучению и расширяет ее возможности, но с другой стороны может порождать данную проблему. Поэтому для решения сложных задач с помощью нейронных сетей необходимо уметь определять и устранять ее.
Причины
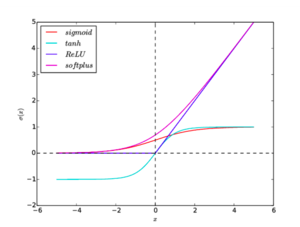
Такая проблема может возникнуть при использовании нейронных сетях классической функцией активации (англ. activation function) сигмоиды (англ. sigmoid):
$\sigma(x) = \frac{1}{1 + e^{-x}}.$
Эта функция часто используется, поскольку множество ее возможных значений — отрезок $[0, 1]$ — совпадает с возможными значениями вероятностной меры, что делает более удобным ее предсказание. Также график сигмоиды соответствует многим естественным процессам, показывающим рост с малых значений, который ускоряется с течением времени, и достигающим своего предела[2] (например, рост популяции).
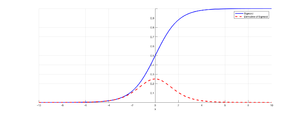
Пусть сеть состоит из подряд идущих нейронов с функцией активации $\sigma(x)$; функция потерть (англ. loss function) $L(y) = MSE(y, \hat{y}) = (y - \hat{y})^2$ (англ. MSE — Mean Square Error); $u_d$ — значение, поступающее на вход нейрону на слое $d$; $w_d$ — вес нейрона на слое $d$; $y$ — выход из последнего слоя. Оценим частные производные по весам такой нейронной сети на каждом слое. Оценка для производной сигмоиды видна из рисунка 1.
$\frac{\partial(L(y))}{\partial(w_d)} = \frac{\partial(L(y))}{\partial(y)} \cdot \frac{\partial(y)}{\partial(w_d)} = 2 (y - \hat{y}) \cdot \sigma'(w_d u_d) u_d \leq 2 (y - \hat{y}) \cdot \frac{1}{4} u_d$
$\frac{\partial(L(y))}{\partial(w_{d - 1})} = \frac{\partial(L(y))}{\partial(w_d)} \cdot \frac{\partial(w_d)}{\partial(w_{d - 1})} \leq 2 (y - \hat{y}) \cdot (\frac{1}{4})^2 u_d u_{d-1}$
$\ldots$
Откуда видно, что оценка элементов градиента растет экспоненциально при рассмотрении частных производных по весам слоев в направлении входа в нейронную сеть (уменьшения номера слоя). Это в свою очередь может приводить либо к экспоненциальному росту градиента от слоя к слою, когда входные значения нейронов — числа, по модулю большие $1$, либо к затуханию, когда эти значения — числа, по модулю меньшие $1$.
Однако, входные значения скрытых слоев есть выходные значения функций активаций предшествующих им слоев. В частности, сигмоида насыщается (англ. saturates) при стремлении аргумента к $+\infty$ или $-\infty$, то есть имеет там конечный предел. Это приводит к тому, что более отдаленные слои обучаются медленнее, так как увеличение или уменьшение аргумента насыщенной функции вносит малые изменения, и градиент становится все меньше. Это и есть проблема затухающего градиента.
Способы определения
Взрывающийся градиент
Возникновение проблемы взрывающегося градиента можно определить по следующим признакам:
- Модель плохо обучается на данных, что отражается в высоком значении функции потерь.
- Модель нестабильна, что отражается в значительных скачках значения функции потерь.
- Значение функции потерь принимает значение
NaN.
Более непрозрачные признаки, которые могут подтвердить возникновение проблемы:
- Веса модели растут экспоненциально.
- Веса модели принимают значение
NaN.
Затухающий градиент
Признаки проблемы затухающего градиента:
- Точность модели растет медленно, при этом возможно раннее срабатывание критерия останова, так как алгоритм может решить, что дальнейшее обучение не будет оказывать существенного влияния.
- Градиент ближе к концу показывает более сильные изменения, в то время как градиент ближе к началу почти не показывает никакие изменения.
- Веса модели уменьшаются экспоненциально во время обучения.
- Веса модели стремятся к $0$ во время обучения.
Способы устранения
Использование другой функции активации
Как уже упоминалось выше, подверженность нейронной сети проблемам взрывающегося или затухающего градиента во многом зависит от свойств используемых функций активации. Поэтому правильный их подбор важен для предотвращения описываемых проблем.
Tanh
$\tanh(x) = \frac{e^x - e^{-x}}{e^x + e^{-x}}$
Функция аналогична сигмоиде, но множество возможных значений: $[-1, 1]$. Градиенты при этом сосредоточены около $0$,. Однако, эта функция также насыщается в обоих направлениях, поэтому также может приводить к проблеме затухающего градиента.
ReLU
$h(x) = \max(0, x)$
Функция проста для вычисления и имеет производную, равную либо $1$, либо $0$. Также есть мнение, что именно эта функция используется в биологических нейронных сетях. При этом функция не насыщается на любых положительных значениях, что делает градиент более чувствительным к отдаленным слоям.
Недостатком функции является отсутствие производной в нуле, что можно устранить доопределением производной в нуле слева или справа. Также эту проблему устраняет использование гладкой аппроксимации, Softplus.
Существуют модификации ReLU:
- Noisy ReLU: $h(x) = \max(0, x + \varepsilon), \varepsilon \sim N(0, \sigma(x))$.
- Parametric ReLU: $h(x) = \begin{cases} x & x > 0 \\ \beta x & \text{otherwise} \end{cases}$.
- Leaky ReLU: Paramtetric ReLU со значением $\beta = 0.01$.
Softplus
$h(x) = \ln(1 + e^x)$
Гладкий, везде дифференцируемый аналог функции ReLU, следовательно, наследует все ее преимущества. Однако, эта функция более сложна для вычисления. Эмпирически было выявлено, что по качеству не превосходит ReLU.
Графики всех функций активации приведены на рисунок 2.
Изменение модели
Для решения проблемы может оказаться достаточным сокращение числа слоев. Это связано с тем, что частные производные по весам растут экспоненциально в зависимости от глубины слоя.
В рекуррентных нейронных сетях можно воспользоваться техникой обрезания обратного распространения ошибки по времени, которая заключается в обновлении весов с определенной периодичностью.
Использование Residual blocks
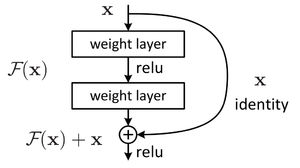
В данной конструкции вывод нейрона подается как следующему нейрону, так и нейрону на расстоянии 2-3 слоев впереди, который суммирует его с выходом предшествующего нейрона, а функция активации в нем — ReLU (см. рисунок 3). Такая связка называется shortcut. Это позволяет при обратном распространении ошибки значениям градиента в слоях быть более чувствительным к градиенту в слоях, с которыми связаны с помощью shortcut, то есть расположенными несколько дальше следующего слоя.
Регуляризация весов
Регуляризация заключается в том, что слишком большие значения весов будут увеличивать функцию потерь. Таким образом, в процессе обучения нейронная сеть помимо оптимизации ответа будет также минимизировать веса, не позволяя им становиться слишком большими.
Обрезание градиента
Образание заключается в ограничении нормы градиента. То есть если норма градиента превышает заранее выбранную величину $T$, то следует масштабировать его так, чтобы его норма равнялась этой величине:
$\nabla_{clipped} = \begin{cases} \nabla & || \nabla || \leq T \\ \frac{T}{|| \nabla ||} \cdot \nabla & \text{otherwise} \end{cases}.$
См. также
- Нейронные сети, перцептрон
- Обратное распространение ошибки
- Регуляризация
- Глубокое обучение
- Сверточные нейронные сети