Мост, эквивалентные определения — различия между версиями
(Добавил ссылку на статью об отношении рёберной двусвязности) |
м (rollbackEdits.php mass rollback) |
||
| (не показаны 2 промежуточные версии 2 участников) | |||
| Строка 44: | Строка 44: | ||
== См.также == | == См.также == | ||
* [[Точка сочленения, эквивалентные определения]] | * [[Точка сочленения, эквивалентные определения]] | ||
| + | * [[Использование обхода в глубину для поиска мостов]] | ||
==Источники информации== | ==Источники информации== | ||
Текущая версия на 19:06, 4 сентября 2022
Пусть — связный граф.
| Определение: |
| Мост (англ. bridge) графа — ребро, соединяющее две компоненты реберной двусвязности . |
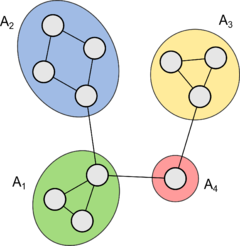
Пример графа с тремя мостами
Эквивалентные определения
| Определение: |
| Мост графа — ребро, при удалении которого граф становится несвязным. |
| Определение: |
| Ребро является мостом графа , если в существуют такие вершины и , что любой простой путь между этими вершинами проходит через ребро |
| Определение: |
| Ребро является мостом графа , если существует разбиение множества вершин на такие множества и , что и ребро принадлежит любому простому пути . |
| Теорема: |
Определения (1), (2), (3) и (4) эквивалентны. |
| Доказательство: |
|
Пусть ребро соединяет вершины и . Пусть граф — связный. Тогда между вершинами и существует еще один путь, т.е. между вершинами и существуют два реберно-непересекающихся пути. Но тогда ребро не является мостом графа . Противоречие. В условиях определения (4) пусть существуют такие вершины и , что между ними существует простой путь . Но тогда граф — связный. Противоречие. Возьмем и . Тогда простой путь содержит ребро . Утверждение доказано Пусть . Пусть ребро не является мостом по определению (1). Тогда между вершинами и есть простой путь . Составим такой путь , что . Сделаем путь простым. Получим простой путь , не проходящий по ребру . Противоречие. |
См.также
Источники информации
- Харари Ф. Теория графов. М.: Мир, 1973. (Изд. 3, М.: КомКнига, 2006. — 296 с.)