Дерево отрезков. Построение — различия между версиями
Serega (обсуждение | вклад) м (→Структура) |
м (rollbackEdits.php mass rollback) |
||
| (не показано 147 промежуточных версий 22 участников) | |||
| Строка 1: | Строка 1: | ||
| − | '''Дерево отрезков''' {{---}} это структура данных, которая позволяет | + | '''Дерево отрезков''' (англ. ''Segment tree'') {{---}} это структура данных, которая позволяет за асимптотику <tex>O(\log n)</tex> реализовать любые операции, определяемые на множестве, на котором данная операция ассоциативна, и существует нейтральный элемент относительно этой операции, то есть на [[Моноид | моноиде]]. Например, суммирование на множестве натуральных чисел, поиск минимума на любом числовом множестве, перемножение матриц на множестве матриц размера <tex>N*N</tex>, объединение множеств, поиск наибольшего общего делителя на множестве целых чисел и многочленов. |
| + | |||
| + | При этом дополнительно возможно изменение элементов массива: как изменение значения одного элемента, так и [[Несогласованные поддеревья. Реализация массового обновления | изменение элементов на целом подотрезке массива]], например разрешается присвоить всем элементам <tex>a[l \ldots r]</tex> какое-либо значение, либо прибавить ко всем элементам массива какое-либо число. Структура занимает <tex>O(n)</tex> памяти, а ее построение требует <tex>O(n)</tex> времени. | ||
==Структура== | ==Структура== | ||
| − | + | Структура представляет собой дерево, листьями которого являются элементы исходного массива. Другие вершины этого дерева имеют по <tex>2</tex> ребенка и содержат результат операции от своих детей (например минимум или сумму). Таким образом, корень содержит результат искомой функции от всего массива <tex>[0\ldots n-1]</tex>, левый ребёнок корня содержит результат функции на <tex dpi=120>[0\ldots\dfrac{n}{2}]</tex>, а правый, соответственно результат на <tex dpi=120>[\dfrac{n}{2}+1\ldots n-1]</tex>. И так далее, продвигаясь вглубь дерева. | |
==Построение дерева== | ==Построение дерева== | ||
| − | Пусть исходный массив <tex | + | Пусть исходный массив <tex>a</tex> состоит из <tex>n</tex> элементов. Для удобства построения увеличим длину массива <tex>a</tex> так, чтобы она равнялась ближайшей степени двойки, т.е. <tex>2^k</tex>, где <tex>2^k \geqslant n</tex>. Это сделано, для того чтобы не допустить обращение к несуществующим элементам массива при дальнейшем процессе построения. Пустые элементы необходимо заполнить нейтральными элементами моноида. Тогда для хранения дерева отрезков понадобится массив <tex>t</tex> из <tex>2^{k+1}</tex> элементов, поскольку в худшем случае количество вершин в дереве можно оценить суммой <tex>n+\dfrac{n}{2}+\dfrac{n}{4} \ldots +1 < 2n</tex>, где <tex>n=2^k</tex>. Таким образом, структура занимает линейную память. |
| + | |||
| + | Процесс построения дерева заключается в заполнении массива <tex>t</tex>. Заполним этот массив таким образом, чтобы <tex>i</tex>-й элемент являлся бы результатом некоторой бинарной операции (для каждой конкретной задачи своей) от элементов c номерами <tex>2i+1</tex> и <tex>2i+2</tex>, то есть родитель являлся результатом бинарной операции от своих сыновей (обозначим в коде эту операцию как "<tex> \circ </tex>"). Один из вариантов — делать рекурсивно. Пусть у нас имеются исходный массив <tex>a</tex>, а также переменные <tex>\mathtt{tl}</tex> и <tex>\mathtt{tr}</tex>, обозначающие границы текущего полуинтервала. Запускаем процедуру построения от корня дерева отрезков (<tex>i=0</tex>, <tex>\mathtt{tl}=0</tex>, <tex>\mathtt{tr}=n</tex>), а сама процедура построения, если её вызвали не от листа, вызывает себя от каждого из двух сыновей и суммирует вычисленные значения, а если её вызвали от листа — то просто записывает в себя значение этого элемента массива (Для этого у нас есть исходный массив <tex> a </tex>). Асимптотика построения дерева отрезков составит, таким образом, <tex>O(n)</tex>. | ||
| + | |||
| + | Выделяют два основных способа построения дерева отрезков: построение снизу и построение сверху. При построении [[Реализация запроса в дереве отрезков снизу | снизу]] алгоритм поднимается от листьев к корню (Просто начинаем заполнять элементы массива <tex>t</tex> от большего индекса к меньшему, таким образом при заполнении элемента <tex> i </tex> его дети <tex>2i+1</tex> и <tex>2i+2</tex> уже будут заполнены, и мы с легкостью посчитаем бинарную операцию от них), а при построении [[Реализация запроса в дереве отрезков сверху | сверху]] спускается от корня к листьям. Особенные изменения появляются в реализации запросов к таким деревьям отрезков. | ||
| + | |||
| + | [[Файл:Segment_tree.png|Пример дерева отрезков для минимума]] | ||
| + | |||
| + | Реализация построения сверху: | ||
| + | |||
| + | '''function''' treeBuild('''T''' a[], '''int''' i, '''int''' tl, '''int''' tr): <font color=green>// мы находимся в вершине с номером i, который отвечает за полуинтервал [tl, tr) </font> | ||
| + | '''if''' tr - tl == 1 | ||
| + | t[i] = a[tl] | ||
| + | '''else''' | ||
| + | tm = (tl + tr) / 2 <font color=green>// середина отрезка</font> | ||
| + | treeBuild(a, 2 * i + 1, tl, tm) | ||
| + | treeBuild(a, 2 * i + 2, tm, tr) | ||
| + | t[i] = t[2 * i + 1] <tex> \circ </tex> t[2 * i + 2] | ||
| + | |||
| + | Реализация построения снизу: | ||
| + | |||
| + | '''function''' treeBuild('''T''' a[]): | ||
| + | '''for''' i = 0 '''to''' n - 1 | ||
| + | t[n - 1 + i] = a[i] | ||
| + | '''for''' i = n - 2 '''downto''' 0 | ||
| + | t[i] = t[2 * i + 1] <tex> \circ </tex> t[2 * i + 2] | ||
| + | |||
| + | ==См. также== | ||
| + | * [[Реализация запроса в дереве отрезков сверху]] | ||
| − | + | *[[Реализация запроса в дереве отрезков снизу]] | |
| − | + | *[[Несогласованные поддеревья. Реализация массового обновления]] | |
| − | + | ==Источники информации== | |
| + | * [http://habrahabr.ru/post/115026/ Хабрахабр — Статья Максима Ахмедова] | ||
| − | + | * [http://rain.ifmo.ru/cat/view.php/vis/trees/segment-2006 Дискретная математика: Алгоритмы — Визуализатор дерева отрезков] | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| + | * [http://e-maxx.ru/algo/segment_tree MAXimal :: algo :: Дерево отрезков] | ||
| − | + | * [http://ru.wikipedia.org/wiki/%D0%94%D0%B5%D1%80%D0%B5%D0%B2%D0%BE_%D0%BE%D1%82%D1%80%D0%B5%D0%B7%D0%BA%D0%BE%D0%B2 Википедия — Дерево отрезков] | |
| − | [http:// | ||
| − | [http:// | + | * [http://ru.wikipedia.org/wiki/Моноид Википедия — Моноид] |
| − | [ | + | [[Категория: Дискретная математика и алгоритмы]] |
| + | [[Категория: Дерево отрезков]] | ||
| + | [[Категория: Структуры данных]] | ||
Текущая версия на 19:43, 4 сентября 2022
Дерево отрезков (англ. Segment tree) — это структура данных, которая позволяет за асимптотику реализовать любые операции, определяемые на множестве, на котором данная операция ассоциативна, и существует нейтральный элемент относительно этой операции, то есть на моноиде. Например, суммирование на множестве натуральных чисел, поиск минимума на любом числовом множестве, перемножение матриц на множестве матриц размера , объединение множеств, поиск наибольшего общего делителя на множестве целых чисел и многочленов.
При этом дополнительно возможно изменение элементов массива: как изменение значения одного элемента, так и изменение элементов на целом подотрезке массива, например разрешается присвоить всем элементам какое-либо значение, либо прибавить ко всем элементам массива какое-либо число. Структура занимает памяти, а ее построение требует времени.
Структура
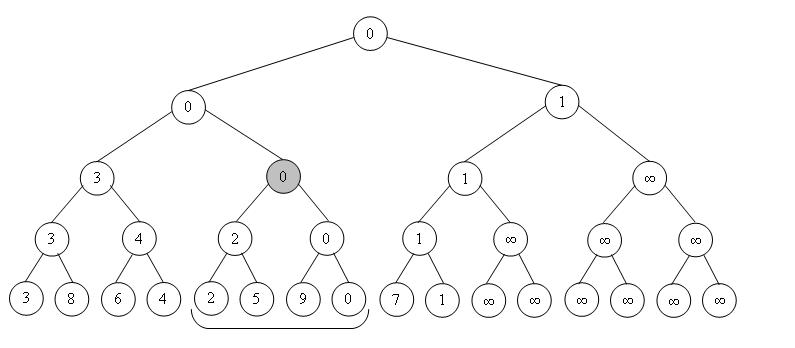
Структура представляет собой дерево, листьями которого являются элементы исходного массива. Другие вершины этого дерева имеют по ребенка и содержат результат операции от своих детей (например минимум или сумму). Таким образом, корень содержит результат искомой функции от всего массива , левый ребёнок корня содержит результат функции на , а правый, соответственно результат на . И так далее, продвигаясь вглубь дерева.
Построение дерева
Пусть исходный массив состоит из элементов. Для удобства построения увеличим длину массива так, чтобы она равнялась ближайшей степени двойки, т.е. , где . Это сделано, для того чтобы не допустить обращение к несуществующим элементам массива при дальнейшем процессе построения. Пустые элементы необходимо заполнить нейтральными элементами моноида. Тогда для хранения дерева отрезков понадобится массив из элементов, поскольку в худшем случае количество вершин в дереве можно оценить суммой , где . Таким образом, структура занимает линейную память.
Процесс построения дерева заключается в заполнении массива . Заполним этот массив таким образом, чтобы -й элемент являлся бы результатом некоторой бинарной операции (для каждой конкретной задачи своей) от элементов c номерами и , то есть родитель являлся результатом бинарной операции от своих сыновей (обозначим в коде эту операцию как ""). Один из вариантов — делать рекурсивно. Пусть у нас имеются исходный массив , а также переменные и , обозначающие границы текущего полуинтервала. Запускаем процедуру построения от корня дерева отрезков (, , ), а сама процедура построения, если её вызвали не от листа, вызывает себя от каждого из двух сыновей и суммирует вычисленные значения, а если её вызвали от листа — то просто записывает в себя значение этого элемента массива (Для этого у нас есть исходный массив ). Асимптотика построения дерева отрезков составит, таким образом, .
Выделяют два основных способа построения дерева отрезков: построение снизу и построение сверху. При построении снизу алгоритм поднимается от листьев к корню (Просто начинаем заполнять элементы массива от большего индекса к меньшему, таким образом при заполнении элемента его дети и уже будут заполнены, и мы с легкостью посчитаем бинарную операцию от них), а при построении сверху спускается от корня к листьям. Особенные изменения появляются в реализации запросов к таким деревьям отрезков.
Реализация построения сверху:
function treeBuild(T a[], int i, int tl, int tr): // мы находимся в вершине с номером i, который отвечает за полуинтервал [tl, tr)
if tr - tl == 1
t[i] = a[tl]
else
tm = (tl + tr) / 2 // середина отрезка
treeBuild(a, 2 * i + 1, tl, tm)
treeBuild(a, 2 * i + 2, tm, tr)
t[i] = t[2 * i + 1] t[2 * i + 2]
Реализация построения снизу:
function treeBuild(T a[]):
for i = 0 to n - 1
t[n - 1 + i] = a[i]
for i = n - 2 downto 0
t[i] = t[2 * i + 1] t[2 * i + 2]