Этапы обработки запроса. Перезапись запросов — различия между версиями
(→Обработка запроса) |
м (rollbackEdits.php mass rollback) |
||
| (не показано 20 промежуточных версий 3 участников) | |||
| Строка 66: | Строка 66: | ||
=== Обработка запроса === | === Обработка запроса === | ||
| − | По большому счету sql базы данных отличаются двумя вещами - тем, как они поддерживают транзакции и тем, насколько хорошо у них умеет работать планировщик запросов. | + | По большому счету sql базы данных отличаются двумя вещами - тем, как они поддерживают транзакции и тем, насколько хорошо у них умеет работать планировщик запросов. |
| − | Общий план: | + | |
| + | '''Общий план:''' | ||
* На вход приходит sql. | * На вход приходит sql. | ||
* Отправляем его в разборщик запросов(парсер). Он на выходе выдаст реляционную алгебру. | * Отправляем его в разборщик запросов(парсер). Он на выходе выдаст реляционную алгебру. | ||
| Строка 73: | Строка 74: | ||
* Реляционная алгебра передается в исполнитель запроса, который ее исполняет. Исполнитель запроса взаимодействует с источником данных в тот момент, когда ему понадобились данные для исполнения запросов. | * Реляционная алгебра передается в исполнитель запроса, который ее исполняет. Исполнитель запроса взаимодействует с источником данных в тот момент, когда ему понадобились данные для исполнения запросов. | ||
| − | Планировщики делятся на две части: | + | '''Планировщики делятся на две части:''' |
==== Перезапись и планировщик ==== | ==== Перезапись и планировщик ==== | ||
Перезапись запроса. Составляет некоторый набор фиксированных правил, которые не зависят от конкретного запроса | Перезапись запроса. Составляет некоторый набор фиксированных правил, которые не зависят от конкретного запроса | ||
| Строка 116: | Строка 117: | ||
==== Преобразование подзапросов ==== | ==== Преобразование подзапросов ==== | ||
| − | + | Реляционное исчисление преобразуется в реляционную алгебру. Если была запись в реляционном исчислении, то у нее вынесли кванторы и преобразовали в реляционную алгебру на основе подхода. Для любого запроса в терминах реляционного исчисления можно построить запрос в терминах реляционной алгебры. | |
Начиная с этого момента оперируем '''только реляционной алгеброй''' | Начиная с этого момента оперируем '''только реляционной алгеброй''' | ||
| Строка 125: | Строка 126: | ||
==== Преобразование соединений ==== | ==== Преобразование соединений ==== | ||
| − | + | Сначала избавляемся от внешних соединений. Внешние соединения — это надстройка над обычными соединениями и более простыми операциями. | |
*Внешние соединения | *Внешние соединения | ||
**$R_1 ⟗_θ R_2 ⇒ (R_1 ⟕_θ R_2) ∪ (R_1 ⟖_θ R_2)$ | **$R_1 ⟗_θ R_2 ⇒ (R_1 ⟕_θ R_2) ∪ (R_1 ⟖_θ R_2)$ | ||
| Строка 135: | Строка 136: | ||
=== Унарные операции === | === Унарные операции === | ||
| − | Мы минимизировали набор операций. | + | Мы минимизировали набор операций. У нас остались унарные операции — фильтр и проекция. |
==== Повторная фильтрация ==== | ==== Повторная фильтрация ==== | ||
| Строка 142: | Строка 143: | ||
**Повторное применение фильтрации заменяется одинарным | **Повторное применение фильтрации заменяется одинарным | ||
**$σ_{cond_1}(σ_{cond_2}(R)) ⇒ σ_{cond_1 ∧ cond_2}(R)$ | **$σ_{cond_1}(σ_{cond_2}(R)) ⇒ σ_{cond_1 ∧ cond_2}(R)$ | ||
| − | + | ||
| − | |||
*Пример | *Пример | ||
**$π_{FirstName}(σ_{Name=M34391}(σ_{S.GId=G.GId}(S × G))) ⇒ π_{FirstName}(σ_{Name=M34391 ∧ S.GId=G.GId}(S × G))$ | **$π_{FirstName}(σ_{Name=M34391}(σ_{S.GId=G.GId}(S × G))) ⇒ π_{FirstName}(σ_{Name=M34391 ∧ S.GId=G.GId}(S × G))$ | ||
| − | + | Cразу объединим фильтр связанный с естественным соединением и фильтр по номеру группы в общий фильтр с конъюнкцией. | |
==== Повторная проекция ==== | ==== Повторная проекция ==== | ||
Если есть несколько проекций, то можно заменить на одну внешнюю проекцию. | Если есть несколько проекций, то можно заменить на одну внешнюю проекцию. | ||
| Строка 153: | Строка 153: | ||
**$π_{A}(π_{B}(R)) ⇒ π_{A}(R)$ | **$π_{A}(π_{B}(R)) ⇒ π_{A}(R)$ | ||
| − | |||
*Пример | *Пример | ||
**$π_{FirstName}(π_{FirstName, Name}(S × G)) ⇒ π_{FirstName}(S × G)$ | **$π_{FirstName}(π_{FirstName, Name}(S × G)) ⇒ π_{FirstName}(S × G)$ | ||
| + | Сразу все спроецируем на имя студента. | ||
==== Проекция и фильтрация ==== | ==== Проекция и фильтрация ==== | ||
| − | Как работать со смесью проекций и фильтраций? Утверждение | + | Как работать со смесью проекций и фильтраций? |
| + | |||
| + | {{Утверждение | ||
| + | |statement= | ||
| + | Фильтрацию всегда можно осуществлять до проекции. | ||
| + | }} | ||
| + | |||
*Правило | *Правило | ||
**Фильтрация осуществляется до проекции | **Фильтрация осуществляется до проекции | ||
**$σ_{cond}(π_{A}(R)) ⇒ π_{A}(σ_{cond}(R))$ | **$σ_{cond}(π_{A}(R)) ⇒ π_{A}(σ_{cond}(R))$ | ||
| − | + | Обратим внимание, что в обратном порядке мы делать не можем, не можем вытаскивать фильтр из-под проекции, так как фильтр может зависеть от тех столбцов, которые проекция удалит. | |
| + | |||
*Пример | *Пример | ||
** $π_{FirstName}(σ_{Name=M34391}(π_{FirstName, Name}(S × G))) ⇒ π_{FirstName}(π_{FirstName, Name}(σ_{Name=M34391}(S × G))) ⇒ π_{FirstName}(σ_{Name=M34391}(S × G))$ | ** $π_{FirstName}(σ_{Name=M34391}(π_{FirstName, Name}(S × G))) ⇒ π_{FirstName}(π_{FirstName, Name}(σ_{Name=M34391}(S × G))) ⇒ π_{FirstName}(σ_{Name=M34391}(S × G))$ | ||
| + | Сначала спроецировали, потом отфильтровали и опять спроецировали. Давайте перенесем фильтр во внутрь проекции. Две внешние операции оказываются проекциями. Можем склеить их в одну проекцию с конъюнкцией. | ||
| − | |||
=== Алгебраические свойства операций === | === Алгебраические свойства операций === | ||
==== Дистрибутивность операций ==== | ==== Дистрибутивность операций ==== | ||
| − | |||
| − | + | '''Фильтрация''' | |
| − | + | Мы можем пользовать стандартными алгебраическими трюками. Предположим хотим отфильтровать объединение. Можем отфильтровать первый аргумент, потом второй, а потом объединить. | |
| + | {{Утверждение | ||
| + | |statement= | ||
| + | $σ_{cond}(R_1 ∪ R_2) ⇒ σ_{cond}(R_1) ∪ σ_{cond}(R_2)$ | ||
| + | }} | ||
| − | + | Аналогично для пересечения | |
| − | + | {{Утверждение | |
| − | + | |statement= | |
| − | + | $σ_{cond}(R_1 ∩ R_2) ⇒ σ_{cond}(R_1) ∩ σ_{cond}(R_2)$ | |
| − | + | }} | |
| − | |||
| − | + | Аналогично для разности | |
| + | {{Утверждение | ||
| + | |statement= | ||
| + | $σ_{cond}(R_1 - R_2) ⇒ σ_{cond}(R_1) - σ_{cond}(R_2)$ | ||
| + | }} | ||
| − | + | Естественное соединение. Если можем разделить условие на две части, одна из которых относится проверяет атрибуты только из левого атрибута, а вторая только из правого, то мы можем протолкнуть этот фильтр отдельно в левый и правый аргумент, а потом соединить только для строк, удовлетворяющим своим половинкам фильтра. | |
| + | Аналогично для разности | ||
| + | {{Утверждение | ||
| + | |statement= | ||
| + | $σ_{cond_1 ∧ cond_2}(R_1 ⋈ R_2) ⇒ σ_{cond_1}(R_1) ⋈ σ_{cond_2}(R_2)$ | ||
| + | }} | ||
| + | |||
| + | '''Проекция''' | ||
| − | + | Можем безопасно проекцировать результат объединения | |
| + | {{Утверждение | ||
| + | |statement= | ||
| + | $π_A(R_1 ∪ R_2) ⇒ π_A(R_1) ∪ π_A(R_2)$ | ||
| + | }} | ||
| − | + | Не можем безопасно проецировать результат пересечения, потому что слева могли быть кортежи, которые кроме атрибута $A$ содержат еще какой-то дополнительный атрибут $X$. Они различались, вошли в пересечение и уже потом мы их спроецируем. Если же сначала сделать проекцию, то этот атрибут $X$ теряется и два кортежа с одинаковым атрибутом $A$ но разным атрибутом $X$ для нас станут неразличимы. | |
| − | + | {{Утверждение | |
| − | + | |statement= | |
| − | + | $π_A(R_1 ∩ R_2) ⇏ π_A(R_1) ∩ π_A(R_2)$ | |
| − | + | }} | |
| − | |||
| − | |||
| + | Аналогично для разности | ||
| + | {{Утверждение | ||
| + | |statement= | ||
| + | $π_A(R_1 - R_2) ⇏ π_A(R_1) - π_A(R_2)$ | ||
| + | }} | ||
| + | |||
| + | С естественным соединением все чуть сложнее. Протолкнем в проекцию только те атрибуты, которые были из левого аргумента, вправо только те, которые были из правого. Но зачем мы делаем $A ∪ R_2$, зачем $R_2$? Именно по $R_2$ мы будем соединять, по ним проводилось естественное соединение. Аналогично $A ∪ R_1$. Внешняя проекция нужна для того, чтобы избавиться от тех атрибутов, которые мы потенциально могли добавить в левой и правой части. | ||
| + | {{Утверждение | ||
| + | |statement= | ||
| + | $π_{A}(R_1 ⋈ R_2) ⇒ π_A(π_{(A ∪ R_2) ∩ R_1}(R_1) ⋈ π_{(A ∪ R_1) ∩ R_2}(R_2))$ | ||
| + | }} | ||
==== Коммутативность операций ==== | ==== Коммутативность операций ==== | ||
| + | |||
| + | За счет коммутативности можем выбирать какая сторона считается левой, а какая правой. Это полезно, потому что можем не делать дублирующиеся методы, когда они не симметричны. | ||
*Коммутативные операции | *Коммутативные операции | ||
| Строка 209: | Строка 244: | ||
**$\div$, $⋇$ | **$\div$, $⋇$ | ||
| − | |||
*Применение коммутативности | *Применение коммутативности | ||
** Выбор левой и правой стороны для несимметричных методов исполнения | ** Выбор левой и правой стороны для несимметричных методов исполнения | ||
==== Ассоциативность операций ==== | ==== Ассоциативность операций ==== | ||
| + | Для ассоциативных операция можем выбирать порядок в котором будет эти ассоциативные операции применять. Мы можем рассматривать не конкретное дерево, которое получилось в результате разбора, а плоский набор отношений и ассоциативные операции между ними, а дальше в каком порядке будет выполнять операции и расставлять скобки зависит уже от нас. | ||
*Ассоциативные операции | *Ассоциативные операции | ||
| Строка 224: | Строка 259: | ||
**$\div$, $⋇$ | **$\div$, $⋇$ | ||
| − | |||
*Применение ассоциативности | *Применение ассоциативности | ||
**Выбор порядка выполнения операций | **Выбор порядка выполнения операций | ||
| Строка 237: | Строка 271: | ||
**$a > b ∧ b > c ⇒ a > b ∧ b > c ∧ a > c$ | **$a > b ∧ b > c ⇒ a > b ∧ b > c ∧ a > c$ | ||
Переразбить условие и запихнуть часть из них под соединение. | Переразбить условие и запихнуть часть из них под соединение. | ||
| − | |||
| − | |||
*Пример | *Пример | ||
**$σ_{P_1.p > P_2.p ∧ P_2.p ≥ 60}(P_1 ⋈_{P_1.SId = P_2.SId} P_2) ⇒ σ_{P_1.p > P_2.p ∧ P_2.p ≥ 60 ∧ P_1.p > 60}(P_1 ⋈_{P_1.SId = P_2.SId} P_2) ⇒ σ_{P_1.p > P_2.p}(σ_{p > 60}(P_1) ⋈_{P_1.SId = P_2.SId} σ_{p ≥ 60}(P_2))$ | **$σ_{P_1.p > P_2.p ∧ P_2.p ≥ 60}(P_1 ⋈_{P_1.SId = P_2.SId} P_2) ⇒ σ_{P_1.p > P_2.p ∧ P_2.p ≥ 60 ∧ P_1.p > 60}(P_1 ⋈_{P_1.SId = P_2.SId} P_2) ⇒ σ_{P_1.p > P_2.p}(σ_{p > 60}(P_1) ⋈_{P_1.SId = P_2.SId} σ_{p ≥ 60}(P_2))$ | ||
| + | |||
| + | Оценки, которые принадлежат одному и тому же студенту, причем оценка по первому предмету лучше, чем оценка по второму предмету и по второму предмету есть хотя бы 60 баллов. Замкнув предикат получим, что оценка по первому предмету строго больше 60 баллов ( > 60). Теперь есть условие, которое зависит только от первого экземпляра таблицы оценок и условие, зависящее только от второго экземпляра таблицы оценок. Протолкнем их во внутрь соединения. За счет замыкания предикатов получили новое условие, которое можно протолкнуть в один из операндов. | ||
==== КНФ и ДНФ ==== | ==== КНФ и ДНФ ==== | ||
| − | Некоторые базы данных преобразуют условия в дизъюнктивную или конъюнктивную нормальную форму исходя из соображения, что и ту и другую можно исполнять слева направо, пока не найдем первую лож для КНФ или первую истину для ДНФ. | + | Некоторые базы данных преобразуют условия в дизъюнктивную или конъюнктивную нормальную форму исходя из соображения, что и ту и другую можно исполнять слева направо, пока не найдем первую лож для КНФ или первую истину для ДНФ. При этом можем пересортировать условия в нужном и удобном нам порядке. К примеру более быстрые условия поместить вперед. С другой стороны оптимизатор может более строгие условия, то есть те, которые отсеивают большее количество строк, перемещать вперед. |
| − | |||
| − | При этом можем пересортировать условия в нужном и удобном нам порядке. К примеру более быстрые условия поместить вперед. С другой стороны оптимизатор может более строгие условия, то есть те, которые отсеивают большее количество строк, перемещать вперед. | ||
Превратили все в ассоциативный и коммутативный вид, что позволяет нам произвольным образом переупорядочивать конъюнкты, в случаю КНФ, или дизъюнкты, в случае ДНФ. | Превратили все в ассоциативный и коммутативный вид, что позволяет нам произвольным образом переупорядочивать конъюнкты, в случаю КНФ, или дизъюнкты, в случае ДНФ. | ||
| − | К тому же за счет правил более эффективно вычислять | + | К тому же за счет правил более эффективно вычислять. |
*Преобразование предикатов | *Преобразование предикатов | ||
**Конъюнктивная нормальная форма | **Конъюнктивная нормальная форма | ||
| Строка 272: | Строка 304: | ||
**Неэквивалентные запросы | **Неэквивалентные запросы | ||
**Тот же результат | **Тот же результат | ||
| − | В частности если | + | В частности, если если нас просят спроецировать на имя студентов естественное соединение студентов и групп и мы знаем, что в $Students$ $GroupId$ является внешним ключом, то мы можем сделать вывод, что это просто проецирование на имя таблички студентов. |
*Пример | *Пример | ||
**$π_{FirstName}(Students ⋈ Groups) ⇒ π_{FirstName}(Students)$, если $Students.GId ⊂ Groups.GId$ | **$π_{FirstName}(Students ⋈ Groups) ⇒ π_{FirstName}(Students)$, если $Students.GId ⊂ Groups.GId$ | ||
Текущая версия на 19:08, 4 сентября 2022
В этом разделе будут рассмотрен этап обработки запросов, а именно перезапись запросов
Содержание
Обработка запроса
От выбора плана сильно зависит производительность
Мотивирующий пример
Пример базы данных:
Пусть у нас есть база данных Университет. Есть следующая таблица Students:
- Students(SId, FirstName, LastName, GId, Year)
- $10^4$ записей
- Индексы: (SId) (кластеризованный), (GId)
И следующая таблица Groups:
- Groups(GId, Name)
- $10^3$ записей
- Индексы: (GId) (кластеризованный), (Name)
Запрос:
Будем выбирать студентов группы M3439
Фамилии студентов группы M3439
select LastName from Students natural join Groups where Name = 'M34391'
Планы запросов без индексов
Делаем декартово произведение, на него навешено условие естественного соединения, потом делаем фильтр и потом проецируем.
- План 1
- $π_{FirstName}(σ_{Name=M34391}(σ_{S.GId=G.GId}(S × G)))$
- Получаем $10^4·10^3 + 10^4·10^3 + 10^4 + 20 ≈ 2·10^7$ операций
Сразу делаем естественное соединение без отдельной стадии фильтрации и декартового произведения. Тем не менее в середине все равно строим $10^4·10^3$, но только один раз. Потом опять отфильтруем и спроецируем. Снизили трудозатраты примерно в два раза.
- План 2
- $π_{Name}(σ_{Name=M34391}(S ⋈ G))$
- $10^4·10^3 + 10^4 + 20 ≈ 10^7$ операция
Сначала отфильтруем группы. Это обработать $1000$ групп. Выберем из них 1 группу. Потом переберем $10^4$ студентов. И финальная проекция на $20$ элементов. Снизили время на $3$ порядка!
- План 3
- $π_{Name}(S ⋈ σ_{Name=M34391}(G))$
- $10^3 + 10^4 + 20 ≈ 10^4$ операций
Планы запросов с индексами
Аналогично плану 3, только теперь не перебираем всех студентов, а достаем их из индекса. Если был индекс на основе B дерева глубины $3$. Мы дошли до его листа и достали примерно $20$ студентов из группы. Осталось сделать проекцию, а это еще $20$ операций. В итоге снизили время еще на порядок.
- План 4. Students(GId)
- $π_{Name}(S ⋈ σ_{Name=M34391}(G))$
- $10^3 + (3 + 20) + 20 ≈ 10^3$ операций
Поиск группы тоже можем ускорить, так как есть индекс по имени группы. Он скорее всего поместится в памяти, оценим его глупину как $2$. К этому нам нужно достать инфомрацию об одной из групп. Итого нашли конкретнуб группу, потом сделаем соединение с помощью индекса по GroupId в студентах и финальная проекция.
- План 5. Groups(Name), Students(GId)
- $π_{Name}(S ⋈ σ_{Name=M34391}(G))$
- $2 + (3 + 20) + 20 ≈ 45$ операций
Результат
Начали с $2·10^7$ операций — наиболее медленный план
Закончили $45$ операций — наиболее быстрый план
Разница на много порядков. Сократили время чуть ли не в миллион раз. Выбор плана исполнения запроса очень сильно влияет на скорость работы.
Обработка запроса
По большому счету sql базы данных отличаются двумя вещами - тем, как они поддерживают транзакции и тем, насколько хорошо у них умеет работать планировщик запросов.
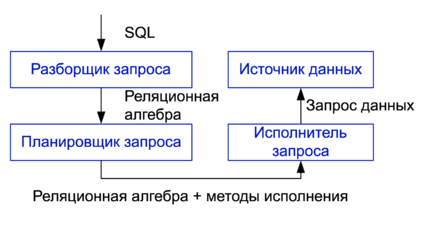
Общий план:
- На вход приходит sql.
- Отправляем его в разборщик запросов(парсер). Он на выходе выдаст реляционную алгебру.
- Затем планировщик запроса снабжает операции реляционной алгебры информацией о том как он собирается их исполнять и в каком порядке.
- Реляционная алгебра передается в исполнитель запроса, который ее исполняет. Исполнитель запроса взаимодействует с источником данных в тот момент, когда ему понадобились данные для исполнения запросов.
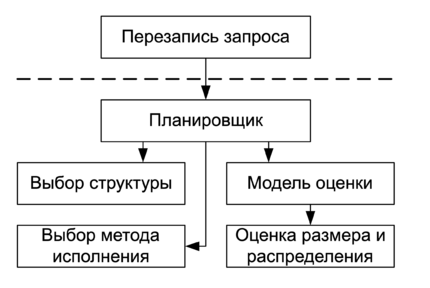
Планировщики делятся на две части:
Перезапись и планировщик
Перезапись запроса. Составляет некоторый набор фиксированных правил, которые не зависят от конкретного запроса
- Перезапись запроса
- Статические правила оптимизации запроса
- СУДБ считает, что оптимизации полезны всегда. Если видит возможность применить правило, то применяет всегда.
Планировщик запроса. Занимается более интеллектуальными вещами, например выбор структуры, выбор методов исполнения. Он очень сильно зависит от модели оценки, которая позволяет ему достаточно точно оценивать объем результатов, которые он должен получить.
- Планировщик запроса
- Принимает решение об оптимизации в зависимости от данных. Может посмотреть например на информацию из индексов.
- В отличии от перезаписи запросов, когда у нас есть формальные правила что и когда нужно делать, планировщику часто приходится перебирать различные варианты исполнения
Выбор структуры и метода
- При выборе структуры:
- Планировщик преобразует запрос. Тут сильно помогают свойства реляционной алгебры, которые позволяют строить альтернативные эквивалентные варианты исполнения
- Планировщик выбирает порядок выполнения операций
- Планировщик выбирает порядок соединений
- Выбор метода исполнения
- Для каждой операции планировщик решает каким конкретно способом операция должна быть исполнена
В итоге получается, что планировщик строит конкретный план, но обычно он строит много различных планов и ему нужно оценить, какой из этих планов будет самым быстрым
Оценка плана
Для оценки эффективности плана у планировщика есть модель стоимости
- Модель стоимости
- Есть стоимость операции
- Есть формулы, которые пересчитывают стоимость операций в зависимости от входных
- Есть формулы, которые пересчитывают стоимость в зависимости от ожидаемых выходных данных
- Оценка размера и распределения
- Часто используется статистика по данным
- Часто используется статистика предыдущих запросов
Перезапись запроса
Минимизация набора операций
Преобразование подзапросов
Реляционное исчисление преобразуется в реляционную алгебру. Если была запись в реляционном исчислении, то у нее вынесли кванторы и преобразовали в реляционную алгебру на основе подхода. Для любого запроса в терминах реляционного исчисления можно построить запрос в терминах реляционной алгебры. Начиная с этого момента оперируем только реляционной алгеброй
- Преобразуются в реляционную алгебру
- Запись в реляционном исчислении
- Вынос кванторов
- Преобразование в алгебру
Преобразование соединений
Сначала избавляемся от внешних соединений. Внешние соединения — это надстройка над обычными соединениями и более простыми операциями.
- Внешние соединения
- $R_1 ⟗_θ R_2 ⇒ (R_1 ⟕_θ R_2) ∪ (R_1 ⟖_θ R_2)$
- $R_1 ⟕_θ R_2 ⇒ σ_θ(R_1 × R_2) ∪ (R_1 - π_{R_1}(σ_θ(R_1 × R_2)))$
- $R_1 ⟖_θ R_2 ⇒ σ_θ(R_1 × R_2) ∪ (R_2 - π_{R_2}(σ_θ(R_1 × R_2)))$
Избавляемся от декартового произведения сказав, что это просто естественное соединения. При необходимости переименуем совпадающие атрибуты, чтобы они случайно не совпали. В будущем будет считать, что совпадающие атрибуты мы переименовываем автоматически. Можем безболезненно делать, така как переименование атрибутов "бесплатно", т.e. O(1). В рантайме никто не оперирует названиями, есть просто номера колонок. Названия просто преобразуются в индексы. На этом уровне нам переименование ровно ничего не стоит.
- Декартово соединение
- $R_1 × R_2 ⇒ R_1 ⋈ R_2$
Унарные операции
Мы минимизировали набор операций. У нас остались унарные операции — фильтр и проекция.
Повторная фильтрация
Если есть два повторных применения фильтрации, то давайте отфильтруем по конъюнкции. Если внутреннее условие очень слабо фильтрует, то в лучшем случае мы ускоримся в два раза.
- Правило
- Повторное применение фильтрации заменяется одинарным
- $σ_{cond_1}(σ_{cond_2}(R)) ⇒ σ_{cond_1 ∧ cond_2}(R)$
- Пример
- $π_{FirstName}(σ_{Name=M34391}(σ_{S.GId=G.GId}(S × G))) ⇒ π_{FirstName}(σ_{Name=M34391 ∧ S.GId=G.GId}(S × G))$
Cразу объединим фильтр связанный с естественным соединением и фильтр по номеру группы в общий фильтр с конъюнкцией.
Повторная проекция
Если есть несколько проекций, то можно заменить на одну внешнюю проекцию.
- Правило
- Повторное применение проекции заменяется внешней
- $π_{A}(π_{B}(R)) ⇒ π_{A}(R)$
- Пример
- $π_{FirstName}(π_{FirstName, Name}(S × G)) ⇒ π_{FirstName}(S × G)$
Сразу все спроецируем на имя студента.
Проекция и фильтрация
Как работать со смесью проекций и фильтраций?
| Утверждение: |
Фильтрацию всегда можно осуществлять до проекции. |
- Правило
- Фильтрация осуществляется до проекции
- $σ_{cond}(π_{A}(R)) ⇒ π_{A}(σ_{cond}(R))$
Обратим внимание, что в обратном порядке мы делать не можем, не можем вытаскивать фильтр из-под проекции, так как фильтр может зависеть от тех столбцов, которые проекция удалит.
- Пример
- $π_{FirstName}(σ_{Name=M34391}(π_{FirstName, Name}(S × G))) ⇒ π_{FirstName}(π_{FirstName, Name}(σ_{Name=M34391}(S × G))) ⇒ π_{FirstName}(σ_{Name=M34391}(S × G))$
Сначала спроецировали, потом отфильтровали и опять спроецировали. Давайте перенесем фильтр во внутрь проекции. Две внешние операции оказываются проекциями. Можем склеить их в одну проекцию с конъюнкцией.
Алгебраические свойства операций
Дистрибутивность операций
Фильтрация
Мы можем пользовать стандартными алгебраическими трюками. Предположим хотим отфильтровать объединение. Можем отфильтровать первый аргумент, потом второй, а потом объединить.
| Утверждение: |
$σ_{cond}(R_1 ∪ R_2) ⇒ σ_{cond}(R_1) ∪ σ_{cond}(R_2)$ |
Аналогично для пересечения
| Утверждение: |
$σ_{cond}(R_1 ∩ R_2) ⇒ σ_{cond}(R_1) ∩ σ_{cond}(R_2)$ |
Аналогично для разности
| Утверждение: |
$σ_{cond}(R_1 - R_2) ⇒ σ_{cond}(R_1) - σ_{cond}(R_2)$ |
Естественное соединение. Если можем разделить условие на две части, одна из которых относится проверяет атрибуты только из левого атрибута, а вторая только из правого, то мы можем протолкнуть этот фильтр отдельно в левый и правый аргумент, а потом соединить только для строк, удовлетворяющим своим половинкам фильтра. Аналогично для разности
| Утверждение: |
$σ_{cond_1 ∧ cond_2}(R_1 ⋈ R_2) ⇒ σ_{cond_1}(R_1) ⋈ σ_{cond_2}(R_2)$ |
Проекция
Можем безопасно проекцировать результат объединения
| Утверждение: |
$π_A(R_1 ∪ R_2) ⇒ π_A(R_1) ∪ π_A(R_2)$ |
Не можем безопасно проецировать результат пересечения, потому что слева могли быть кортежи, которые кроме атрибута $A$ содержат еще какой-то дополнительный атрибут $X$. Они различались, вошли в пересечение и уже потом мы их спроецируем. Если же сначала сделать проекцию, то этот атрибут $X$ теряется и два кортежа с одинаковым атрибутом $A$ но разным атрибутом $X$ для нас станут неразличимы.
| Утверждение: |
$π_A(R_1 ∩ R_2) ⇏ π_A(R_1) ∩ π_A(R_2)$ |
Аналогично для разности
| Утверждение: |
$π_A(R_1 - R_2) ⇏ π_A(R_1) - π_A(R_2)$ |
С естественным соединением все чуть сложнее. Протолкнем в проекцию только те атрибуты, которые были из левого аргумента, вправо только те, которые были из правого. Но зачем мы делаем $A ∪ R_2$, зачем $R_2$? Именно по $R_2$ мы будем соединять, по ним проводилось естественное соединение. Аналогично $A ∪ R_1$. Внешняя проекция нужна для того, чтобы избавиться от тех атрибутов, которые мы потенциально могли добавить в левой и правой части.
| Утверждение: |
$π_{A}(R_1 ⋈ R_2) ⇒ π_A(π_{(A ∪ R_2) ∩ R_1}(R_1) ⋈ π_{(A ∪ R_1) ∩ R_2}(R_2))$ |
Коммутативность операций
За счет коммутативности можем выбирать какая сторона считается левой, а какая правой. Это полезно, потому что можем не делать дублирующиеся методы, когда они не симметричны.
- Коммутативные операции
- $⋈$
- $∪$
- $∩$
- Некоммутативные операции
- $-$
- $\div$, $⋇$
- Применение коммутативности
- Выбор левой и правой стороны для несимметричных методов исполнения
Ассоциативность операций
Для ассоциативных операция можем выбирать порядок в котором будет эти ассоциативные операции применять. Мы можем рассматривать не конкретное дерево, которое получилось в результате разбора, а плоский набор отношений и ассоциативные операции между ними, а дальше в каком порядке будет выполнять операции и расставлять скобки зависит уже от нас.
- Ассоциативные операции
- $⋈$
- $∪$
- $∩$
- Неассоциативные операции
- $-$
- $\div$, $⋇$
- Применение ассоциативности
- Выбор порядка выполнения операций
Обработка условий
Замыкание предикатов
Можем извлекать дополнительную информацию, используя замыкание предикатов
- Примеры правил
- $a = b ∧ b = c ⇒ a = b ∧ b = c ∧ a = c$
- $a > b ∧ b = c ⇒ a > b ∧ b = c ∧ a > c$
- $a > b ∧ b > c ⇒ a > b ∧ b > c ∧ a > c$
Переразбить условие и запихнуть часть из них под соединение.
- Пример
- $σ_{P_1.p > P_2.p ∧ P_2.p ≥ 60}(P_1 ⋈_{P_1.SId = P_2.SId} P_2) ⇒ σ_{P_1.p > P_2.p ∧ P_2.p ≥ 60 ∧ P_1.p > 60}(P_1 ⋈_{P_1.SId = P_2.SId} P_2) ⇒ σ_{P_1.p > P_2.p}(σ_{p > 60}(P_1) ⋈_{P_1.SId = P_2.SId} σ_{p ≥ 60}(P_2))$
Оценки, которые принадлежат одному и тому же студенту, причем оценка по первому предмету лучше, чем оценка по второму предмету и по второму предмету есть хотя бы 60 баллов. Замкнув предикат получим, что оценка по первому предмету строго больше 60 баллов ( > 60). Теперь есть условие, которое зависит только от первого экземпляра таблицы оценок и условие, зависящее только от второго экземпляра таблицы оценок. Протолкнем их во внутрь соединения. За счет замыкания предикатов получили новое условие, которое можно протолкнуть в один из операндов.
КНФ и ДНФ
Некоторые базы данных преобразуют условия в дизъюнктивную или конъюнктивную нормальную форму исходя из соображения, что и ту и другую можно исполнять слева направо, пока не найдем первую лож для КНФ или первую истину для ДНФ. При этом можем пересортировать условия в нужном и удобном нам порядке. К примеру более быстрые условия поместить вперед. С другой стороны оптимизатор может более строгие условия, то есть те, которые отсеивают большее количество строк, перемещать вперед.
Превратили все в ассоциативный и коммутативный вид, что позволяет нам произвольным образом переупорядочивать конъюнкты, в случаю КНФ, или дизъюнкты, в случае ДНФ. К тому же за счет правил более эффективно вычислять.
- Преобразование предикатов
- Конъюнктивная нормальная форма
- Дизъюнктивная нормальная форма
- Вычисление КНФ
- Слева направо, до первой лжи
- Вычисление ДНФ
- Слева направо, до первой истины
Семантические оптимизации
Можем применять знания об ограничениях Есть схема, в ней есть Ограничения ключей Ограничения внешних ключей
Формально можем построить не эквивалентный запрос, который всегда будет давать ровно тот же результат. То есть он будет эквивалентен с учетом тех ограничений, которые у нас есть для базы данных.
Семантическая оптимизация
- Применение знания об ограничениях
- Неэквивалентные запросы
- Тот же результат
В частности, если если нас просят спроецировать на имя студентов естественное соединение студентов и групп и мы знаем, что в $Students$ $GroupId$ является внешним ключом, то мы можем сделать вывод, что это просто проецирование на имя таблички студентов.
- Пример
- $π_{FirstName}(Students ⋈ Groups) ⇒ π_{FirstName}(Students)$, если $Students.GId ⊂ Groups.GId$
Обратим внимание, что без ограничения на ключи данное преобразование корректным не является
Пример оптимизации
- Ограничение
- У всех, кто получает стипендию все оценки $≥ 60$
check not HasScolarship or 60 <= all(select Points from Points where Points.SId = Id)
- Запрос
- Оценки стипендиатов группы M34391 по СУБД
select Points from Students natural join Points where HasScolarship and CId = 10 and GId = M34391
- $σ_{HasScolarship ∧ CId = 10}(Students ⋈ Points)$
- Оптимизированный запрос
- $σ_{GId=M34391 ∧ HasScolarship}(Students) ⋈ σ_{60 ≥ Points ∧ CId = 10}(Points)$
Литература
- Дейт К. Введение в системы баз данных (глава 18)