Сведение задачи LCA к задаче RMQ — различия между версиями
(→Алгоритм) |
м (rollbackEdits.php mass rollback) |
||
| (не показано 59 промежуточных версий 15 участников) | |||
| Строка 1: | Строка 1: | ||
| − | = | + | {{Шаблон:Задача |
| + | |definition = | ||
| + | Пусть дано корневое дерево <tex>T</tex>. На вход подаются запросы вида <tex>(u,\;v)</tex>, для каждого запроса требуется найти их наименьшего общего предка. | ||
| + | }} | ||
{{Определение | {{Определение | ||
| − | |definition = '''Наименьшим общим предком (least common ancestor | + | |id=lca_suf_tree |
| + | |definition = '''Наименьшим общим предком''' (англ. ''least common ancestor'') двух узлов <tex>u</tex> и <tex>v</tex> в корневом дереве <tex>T</tex> называется узел <tex>w</tex>, который среди всех узлов, являющихся предками как узла <tex>u</tex>, так и <tex>v</tex>, имеет наибольшую глубину. | ||
}} | }} | ||
| − | |||
== Алгоритм == | == Алгоритм == | ||
| + | === Идея === | ||
| + | Будем решать задачу <tex>LCA</tex>, уже умея решать задачу <tex>RMQ</tex>. Тогда поиск наименьшего общего предка <tex>i</tex>-того и <tex>j</tex>-того элементов сводится к запросу минимума на отрезке массива, который будет введен позднее. | ||
| + | |||
=== Препроцессинг === | === Препроцессинг === | ||
| − | + | Для каждой вершины <tex>T</tex> определим глубину с помощью следующей рекурсивной формулы: | |
| − | :<tex>depth(u)= \begin{cases} | + | :<tex>\mathrm{depth}(u) = \begin{cases} |
| − | 0 & u = root(T),\\ | + | 0 & u = \mathrm{root}(T),\\ |
| − | depth(v) + 1 & u = son(v). | + | \mathrm{depth}(v) + 1 & u = \mathrm{son}(v). |
\end{cases}</tex> | \end{cases}</tex> | ||
| + | Ясно, что глубина вершины элементарным образом поддерживается во время обхода в глубину. | ||
| + | |||
| + | Запустим [[Обход в глубину, цвета вершин|обход в глубину]] из корня, который будет вычислять значения следующих величин: | ||
| + | #Cписок глубин посещенных вершин <tex>d</tex>. Глубина текущей вершины добавляется в конец списка при входе в данную вершину, а также после каждого возвращения из её сына. | ||
| + | #Список посещений узлов <tex>\mathtt{vtx}</tex>, строящийся аналогично предыдущему, только добавляется не глубина а сама вершина. | ||
| + | #Значение функции <tex>\mathtt{I}[u]</tex>, возвращающей индекс в списке глубин <tex>d</tex>, по которому была записана глубина вершины <tex>u</tex> (например на момент входа в вершину). | ||
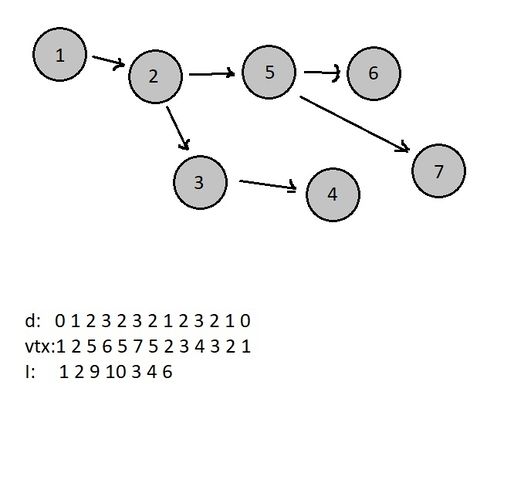
| − | + | Вот таким образом будут выглядеть эти три массива после обхода в глубину: | |
| + | |||
| + | [[Файл:HoD8KSiOzTg.jpg | мини | left | 700x500px| Пример массива <tex>\mathtt{vtx}</tex>]] | ||
| + | <br clear="all"> | ||
=== Запрос === | === Запрос === | ||
| − | + | Будем считать, что <tex>\mathrm{rmq}(d,l,r)</tex> возвращает индекс минимального элемента в <tex>d</tex> на отрезке <tex>[l..r]</tex>. Тогда ответом на запрос <tex>\mathrm{lca}(u, v)</tex>, где <tex>\mathtt{I}[u] \leqslant \mathtt{I}[v]</tex>, будет <tex>\mathtt{vtx}[\mathrm{rmq}(d,\mathtt{I}[u], \mathtt{I}[v])]</tex>. | |
| + | === Доказательство корректности алгоритма === | ||
| + | {{Теорема | ||
| + | |statement= | ||
| + | Наименьшему общему предку вершин <tex>u, v</tex> соответствует минимальная глубина на отрезке <tex>d[\mathtt{I}[u], \mathtt{I}[v]]</tex>. | ||
| + | |proof= | ||
| + | Рассмотрим два узла <tex>u, v</tex> корневого дерева <tex>T</tex>. Рассмотрим отрезок <tex>d[\mathtt{I}[u]..\mathtt{I}[v]]</tex>. Поскольку этот отрезок {{---}} путь из <tex>u</tex> в <tex>v</tex>, он проходит через их наименьшего общего предка <tex>w</tex> (в дереве есть только один простой путь между вершинами), а следовательно минимум на отрезке никак не больше глубины <tex>w</tex>. Заметим, что в момент добавления <tex>\mathtt{I}[u]</tex> обход посещал поддерево с корнем <tex>w</tex>. В момент добавления <tex>\mathtt{I}[v]</tex> мы все еще в поддереве с корнем <tex>w</tex>. Значит, и на отрезке между <tex>\mathtt{I}[u]</tex> и <tex>\mathtt{I}[v]</tex> мы находились внутри поддерева с корнем <tex>w</tex>. Отсюда сделаем заключение, что на рассматриваемом отрезке не посещалась вершина, отличная от <tex>w</tex>, с глубиной меньшей либо равной глубины <tex>w</tex>, т. к. подобной вершины нет в поддереве с корнем <tex>w</tex>. | ||
| + | }}. | ||
| − | == | + | == Пример == |
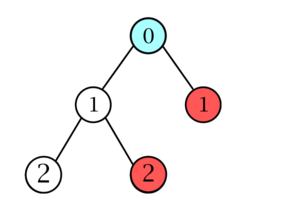
| − | Рассмотрим | + | Рассмотрим дерево на рисунке 1. Найдем наименьшего общего предка вершин, помеченных красным цветом. |
| − | + | Список глубин, получающийся в результате обхода в глубину {{---}} <tex>[0, 1, 2, 1, 2, 1, 0, 1, 0].</tex> | |
| − | + | Глубина наименьшего общего предка красных вершин равна минимуму на отрезке <tex>[2, 1, 0, 1].</tex> | |
| + | [[Файл:Lca to rmq.png(2).png|thumb|center|400x200px|Рисунок к примеру]] | ||
| + | <div style='clear:left;'></div> | ||
== Сложность == | == Сложность == | ||
| − | |||
| − | |||
| − | + | Для нахождения минимального элемента на отрезке можно использовать [[Алгоритм Фарака-Колтона и Бендера|алгоритм Фарака-Колтона и Бендера]] для <tex>\pm 1RMQ</tex>, т. к. соседние элементы в списке глубин отличаются не более чем на единицу. Длина списка глубин составляет <tex>(2n - 1)</tex>, таким образом, препроцессинг работает за <tex>O(n)</tex>. Время выполнения запроса равно времени запроса минимального элемента на отрезке {{---}} <tex>O(1)</tex>. | |
| − | Время выполнения запроса равно времени запроса минимального элемента на отрезке | ||
== См.также == | == См.также == | ||
| Строка 35: | Строка 56: | ||
*[[Алгоритм Фарака-Колтона и Бендера]] | *[[Алгоритм Фарака-Колтона и Бендера]] | ||
*[[Сведение задачи RMQ к задаче LCA]] | *[[Сведение задачи RMQ к задаче LCA]] | ||
| − | == | + | == Источники информации == |
*[http://e-maxx.ru/algo/lca Наименьший общий предок. Нахождение за O (sqrt (N)) и O (log N) с препроцессингом O (N)] | *[http://e-maxx.ru/algo/lca Наименьший общий предок. Нахождение за O (sqrt (N)) и O (log N) с препроцессингом O (N)] | ||
| + | |||
| + | [[Категория: Алгоритмы и структуры данных]] | ||
| + | [[Категория: Задача о наименьшем общем предке]] | ||
Текущая версия на 19:21, 4 сентября 2022
| Задача: |
| Пусть дано корневое дерево . На вход подаются запросы вида , для каждого запроса требуется найти их наименьшего общего предка. |
| Определение: |
| Наименьшим общим предком (англ. least common ancestor) двух узлов и в корневом дереве называется узел , который среди всех узлов, являющихся предками как узла , так и , имеет наибольшую глубину. |
Содержание
Алгоритм
Идея
Будем решать задачу , уже умея решать задачу . Тогда поиск наименьшего общего предка -того и -того элементов сводится к запросу минимума на отрезке массива, который будет введен позднее.
Препроцессинг
Для каждой вершины определим глубину с помощью следующей рекурсивной формулы:
Ясно, что глубина вершины элементарным образом поддерживается во время обхода в глубину.
Запустим обход в глубину из корня, который будет вычислять значения следующих величин:
- Cписок глубин посещенных вершин . Глубина текущей вершины добавляется в конец списка при входе в данную вершину, а также после каждого возвращения из её сына.
- Список посещений узлов , строящийся аналогично предыдущему, только добавляется не глубина а сама вершина.
- Значение функции , возвращающей индекс в списке глубин , по которому была записана глубина вершины (например на момент входа в вершину).
Вот таким образом будут выглядеть эти три массива после обхода в глубину:
Запрос
Будем считать, что возвращает индекс минимального элемента в на отрезке . Тогда ответом на запрос , где , будет .
Доказательство корректности алгоритма
| Теорема: |
Наименьшему общему предку вершин соответствует минимальная глубина на отрезке . |
| Доказательство: |
| Рассмотрим два узла корневого дерева . Рассмотрим отрезок . Поскольку этот отрезок — путь из в , он проходит через их наименьшего общего предка (в дереве есть только один простой путь между вершинами), а следовательно минимум на отрезке никак не больше глубины . Заметим, что в момент добавления обход посещал поддерево с корнем . В момент добавления мы все еще в поддереве с корнем . Значит, и на отрезке между и мы находились внутри поддерева с корнем . Отсюда сделаем заключение, что на рассматриваемом отрезке не посещалась вершина, отличная от , с глубиной меньшей либо равной глубины , т. к. подобной вершины нет в поддереве с корнем . |
Пример
Рассмотрим дерево на рисунке 1. Найдем наименьшего общего предка вершин, помеченных красным цветом. Список глубин, получающийся в результате обхода в глубину — Глубина наименьшего общего предка красных вершин равна минимуму на отрезке
Сложность
Для нахождения минимального элемента на отрезке можно использовать алгоритм Фарака-Колтона и Бендера для , т. к. соседние элементы в списке глубин отличаются не более чем на единицу. Длина списка глубин составляет , таким образом, препроцессинг работает за . Время выполнения запроса равно времени запроса минимального элемента на отрезке — .
См.также
- Метод двоичного подъема
- Решение RMQ с помощью разреженной таблицы
- Алгоритм Фарака-Колтона и Бендера
- Сведение задачи RMQ к задаче LCA