Нормализация набора данных — различия между версиями
м (rollbackEdits.php mass rollback) |
|||
| (не показаны 3 промежуточные версии 2 участников) | |||
| Строка 1: | Строка 1: | ||
| − | + | Набор данных содержит в себе единицы измерения, которые отбрасываются, чтобы набор данных был просто числами. Но чтобы далее работать, нам нужно, чтобы все объекты были приведены к единому формату. С этим и помогает '''нормализация'''. | |
| + | |||
| + | Нормализация применяется независимо к столбцу X. | ||
Важно в sklearn.preprocessing есть метод normalize, но это не то, что нам нужно, он рассматривает нормализацию с геометрической точки зрения | Важно в sklearn.preprocessing есть метод normalize, но это не то, что нам нужно, он рассматривает нормализацию с геометрической точки зрения | ||
| − | (представляет объект в виде вектора), а не по столбцам | + | (представляет объект в виде вектора), а не по столбцам. |
| Строка 17: | Строка 19: | ||
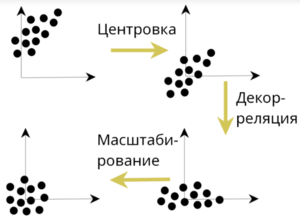
= Декорреляция = | = Декорреляция = | ||
| − | [[File:Декорреляция.png|300px|thumb| | + | Процесс, который используется для уменьшения корреляции. |
| + | [[File:Декорреляция.png|300px|thumb|рис.1 Декорреляция]] | ||
1. Есть матрица X. | 1. Есть матрица X. | ||
Текущая версия на 19:32, 4 сентября 2022
Набор данных содержит в себе единицы измерения, которые отбрасываются, чтобы набор данных был просто числами. Но чтобы далее работать, нам нужно, чтобы все объекты были приведены к единому формату. С этим и помогает нормализация.
Нормализация применяется независимо к столбцу X.
Важно в sklearn.preprocessing есть метод normalize, но это не то, что нам нужно, он рассматривает нормализацию с геометрической точки зрения (представляет объект в виде вектора), а не по столбцам.
Минмакс, [0;1] масштабирование
После нормализации: и
Стандартизация, Z-масштабирование
После нормализации: и
Декорреляция
Процесс, который используется для уменьшения корреляции.
1. Есть матрица X.
2. Матрицу центрировали ().
3. Ковариация вычисляется по следующей формуле:
4. Если же матрица нормализована так, что , то из произведения мы получим не ковариационную, а корреляционную матрицу
5. Декорреляция вычисляется по формуле:
где находится из разложения Холецкого
| Утверждение: |
После декорреляции: |
|
. |