Рёберный граф — различия между версиями
м (rollbackEdits.php mass rollback) |
|||
| Строка 1: | Строка 1: | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
{{Определение | {{Определение | ||
|definition = | |definition = | ||
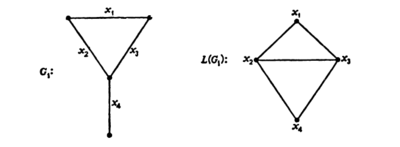
| − | Пусть задан граф <tex>G</tex>, тогда его '''рёберным графом''' <tex>L(G)</tex> | + | Пусть задан граф <tex>G</tex>, тогда его '''рёберным графом''' <tex>L(G)</tex> называется граф, для которого верны следующие утверждения |
* любая вершина графа <tex>L(G)</tex> представляет ребро графа <tex>G</tex>, | * любая вершина графа <tex>L(G)</tex> представляет ребро графа <tex>G</tex>, | ||
* две вершины графа <tex>L(G)</tex> смежны тогда и только тогда, когда их соответствующие рёбра смежны в <tex>G</tex>. | * две вершины графа <tex>L(G)</tex> смежны тогда и только тогда, когда их соответствующие рёбра смежны в <tex>G</tex>. | ||
Текущая версия на 19:19, 4 сентября 2022
| Определение: |
Пусть задан граф , тогда его рёберным графом называется граф, для которого верны следующие утверждения
|
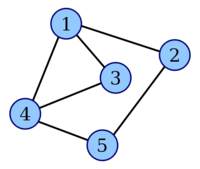
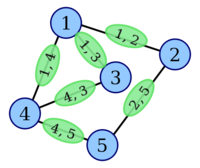
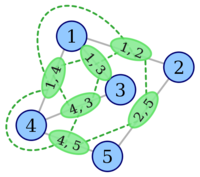
Построение
 |
 |
 |

|
| Граф | Новые вершины | Добавлены рёбра в | Рёберный граф |
Свойства
| Утверждение: |
Рёберный граф связного графа связен. |
| Если связен, он содержит путь, соединяющий любые два его ребра, что переводится в путь графа , содержащий любые две вершины графа . |
| Утверждение: |
Задача о максимальном независимом множестве для рёберного графа соответствует задаче нахождения максимального паросочетания в исходном графе. |
| Утверждение: |
Рёберное хроматическое число графа равно вершинному хроматическому числу его рёберного графа . |
| Утверждение: |
Рёберный граф рёберно-транзитивного графа является вершинно-транзитивным графом. |
| Утверждение: |
Если граф — Эйлеров граф, то его рёберный граф является Гамильтоновым графом. |
| Рассмотрим Эйлеров путь в исходном графе . Составим из вершин реберного графа последовательность , поcтавив в соответсвие ребру вершину . Так как два подряд идущих ребра из исходного пути смежны, то из определения реберного графа следует, что сответствующие подряд идущие вершины в получившейся последовательности смежны. Следовательно мы получили Гамильтонов путь в реберном графе . Доказательство для циклов аналогично. |
| Утверждение: |
Ребра графа можно разбить на полные подграфы таким образом, чтобы ни одна из вершин не принадлежала более чем двум подграфам. |
| Утверждение: |
Реберный граф реберного графа не является исходным графом . |
| Контрпримером является граф из раздела построение. В реберном графе количество вершин равно количеству ребер в исходном. Таким образом, в реберном графе к графу будет вершин, а в исходном графе их всего . |
| Теорема: |
Если — это -граф с вершинами, имеющими степени , то имеет вершин и ребер, где
|
| Доказательство: |
|
По определению реберного графа граф имеет вершин. Каждые ребер, инцидентных вершине , дают вклад в число ребер графа , так что |
Источники информации
- Wikipedia — Реберные графы
- Харари Фрэнк Теория графов: Пер. с англ./ Предисл. В. П. Козырева; Под ред. Г.П.Гаврилова. Изд. 4-е. — М.: Книжный дом "ЛИБРОКОМ", 2009. — 296 с. — ISBN 978-5-397-00622-4.(Глава 8: Реберные графы. стр. 91-104)