Код Шеннона — различия между версиями
м (rollbackEdits.php mass rollback) |
|||
| Строка 1: | Строка 1: | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
'''''Код Шеннона''''' — алгоритм [[Кодирование информации#Префиксный код | префиксного кодирования]] алфавита, предложенный Клодом Шенноном, в котором используется избыточность сообщения, заключённая в неоднородном распределении частот символов первичного алфавита, то есть заменяет коды более частых символов короткими последовательностями, а коды более редких символов — более длинными последовательностями. | '''''Код Шеннона''''' — алгоритм [[Кодирование информации#Префиксный код | префиксного кодирования]] алфавита, предложенный Клодом Шенноном, в котором используется избыточность сообщения, заключённая в неоднородном распределении частот символов первичного алфавита, то есть заменяет коды более частых символов короткими последовательностями, а коды более редких символов — более длинными последовательностями. | ||
{{Определение | {{Определение | ||
Текущая версия на 19:15, 4 сентября 2022
Код Шеннона — алгоритм префиксного кодирования алфавита, предложенный Клодом Шенноном, в котором используется избыточность сообщения, заключённая в неоднородном распределении частот символов первичного алфавита, то есть заменяет коды более частых символов короткими последовательностями, а коды более редких символов — более длинными последовательностями.
| Определение: |
| Пусть — алфавит из различных символов, которому соответствует набор вероятностей такой, что , .
. Тогда набор бинарных кодов , такой, что: 1. не является префиксом для , при 2. представляет собой коэффициентов двоичного разложения числа называется кодом Шеннона. |
Содержание
Алгоритм построения бинарного кода Шеннона
Пусть нам даны наборы и , тогда для нахождения кодовых слов необходимо:
- Отсортировать элементы алфавита по не возрастанию вероятности встречи символа.
- Элементу поставить в соответствие число , при этом .
- Представить каждое число в виде двоичной дроби.
- В качестве кодового слова для использовать первые коэффициентов представления . ( — наименьшее целое число, не меньшее )
Пример
Для примера возьмём алфавит и набор :
| Символ | a | b | c | d | e | f |
|---|---|---|---|---|---|---|
| 0.10 | 0.20 | 0.10 | 0.10 | 0.35 | 0.15 |
По алгоритму сортируем элементы алфавита по не возрастанию :
| Символ | e | b | f | a | c | d |
|---|---|---|---|---|---|---|
| 0.35 | 0.20 | 0.15 | 0.10 | 0.10 | 0.10 |
Каждому символу сопоставляем :
| Символ | e | b | f | a | c | d |
|---|---|---|---|---|---|---|
| 0.00 | 0.35 | 0.55 | 0.70 | 0.80 | 0.90 |
Переведём в двоичную систему счисления:
| Символ | e | b | f | a | c | d |
|---|---|---|---|---|---|---|
| 0.00000 | 0.01010 | 0.10001 | 0.10110 | 0.11001 | 0.11100 |
Посчитаем и запишем коды:
| Символ | e | b | f | a | c | d |
|---|---|---|---|---|---|---|
| 2 | 3 | 3 | 4 | 4 | 4 | |
| Код | 00 | 010 | 100 | 1011 | 1100 | 1110 |
| Утверждение: |
Код Шеннона является префиксным |
|
Для доказательства выбираем два произвольных кодовых слова с номерами и , . Кодовое слово заведомо короче, чем , поэтому достаточно доказать, что эти слова отличаются в одном из первых символов. Рассмотрим разность: = . Длина слова и его вероятность связаны соотношением . Поэтому . С учётом этого неравенства получаем, что . В двоичной записи числа в правой части мы имеем после запятой нулей и единицу в позиции с номером . Поэтому по меньшей мере в одном из разрядов слова и отличаются и, следовательно, не является префиксов для . Это верно для любой пары слов, так как и были выбраны произвольно. Значит, код является префиксным. |
Примечание
Код Шеннона является достаточно старым методом сжатия, который не представляет практического применения на сегодняшний день. Это связано с тем, что в общем случае длина последовательности, полученная кодированием Шеннона, равна длине последовательности, полученной алгоритмом Хаффмана. Но можно привести примеры, на которых метод Шеннона формирует неоптимальные коды. Например, если и набор :
| Символ | a | b | c | d |
|---|---|---|---|---|
| 0.65 | 0.15 | 0.15 | 0.05 | |
| 0 | 0.65 | 0.80 | 0.95 | |
| 1 | 3 | 3 | 5 | |
| Код | 0 | 101 | 110 | 1111 |
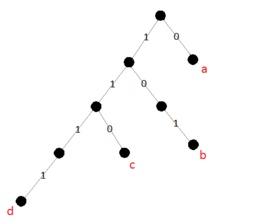
Изобразим полученный результат в виде кодового дерева. Из этого рисунка видно, что полученные кодовые слова для букв и не являются оптимальными, так как их можно сократить на один бит без потери свойства однозначной декодируемости. Поэтому более эффективным считается сжатие метод Хаффмана.
См.также
Источники информации
- Ю. М. Штарьков, “Обобщенные коды Шеннона”, Пробл. передачи информ., 20:3 (1984), 3—16 — с. 4.
- Б. Д. Кудряшов Теория информации. С.—Пб.: Питер, 2009 — с. 36.