Реализация запроса в дереве отрезков снизу — различия между версиями
Gemin (обсуждение | вклад) |
м (rollbackEdits.php mass rollback) |
||
| (не показано 46 промежуточных версий 12 участников) | |||
| Строка 1: | Строка 1: | ||
| − | |||
| − | |||
==Алгоритм== | ==Алгоритм== | ||
| − | [[ | + | |
| − | Будем рассматривать дерево отрезков | + | Реализация запроса снизу вверх в дереве отрезков является, в отличие от [[Реализация запроса в дереве отрезков сверху| реализации запроса сверху вниз]], итеративным методом. Будем рассматривать абстрактную операцию, обладающую свойством ассоциативности, и обозначать ее <tex>a \circ b</tex>. |
| − | Если | + | |
| + | [[Дерево отрезков. Построение|Построим дерево отрезков]], и установим границы отрезка на соответствующие им листья. Будем действовать в 3 этапа: | ||
| + | # Если элемент, попавший на левую границу, является правым сыном, то запишем в результат значение, полученное после выполнения нашей операции над предыдущим результатом и значением этого элемента, а левую границу перемещаем на один элемент вправо. Аналогично с правой границей (является ли она левым сыном). Таким образом мы учтем вклад нужной нам вершины и избавимся от вклада ненужного нам поддерева. | ||
| + | # Устанавливаем границы отрезка на родительские элементы текущих границ. Это позволит узнать, входит ли полученный отрезок в искомый или нет. Повторяем этап 1, пока границы не пересекутся. | ||
| + | # Если после завершения цикла границы совпадут, значит полученный отрезок входит в искомый, и надо пересчитать результат. | ||
| + | |||
| + | {| cellpadding="10" | ||
| + | | '''Реализация запроса снизу вверх''' || '''Ещё один пример''' | ||
| + | |- | ||
| + | | [[Файл:Запрос снизу №1х1.jpg|550px|]] || [[Файл:Запрос снизу №2х1.jpg|550px]] | ||
| + | |- | ||
| + | | [[Файл:Запрос снизу №1х2.jpg|550px|]] || [[Файл:Запрос снизу №2х2.jpg|550px]] | ||
| + | |- | ||
| + | | [[Файл:Запрос снизу №1х3.jpg|550px|]] || [[Файл:Запрос снизу №2х3.jpg|550px]] | ||
| + | |- | ||
| + | | [[Файл:Запрос снизу №1х4.jpg|550px|]] || [[Файл:Запрос снизу №2х4.jpg|550px]] | ||
| + | |} | ||
| + | |||
==Псевдокод== | ==Псевдокод== | ||
| − | |||
| − | + | Пусть результат считаем на отрезке <tex> [left, right] </tex>. При этом значения <tex>left</tex> и <tex>right</tex>, передающиеся в функцию, должны указывать на листья дерева (необходимо увеличить значение на индекс массива, с которого начинаются листья). Переменные <tex>leftRes</tex> и <tex>rightRes</tex> будут собирать значения на отрезках, отделившихся соответственно слева или справа от рассматриваемого. | |
| − | + | ||
| − | while left < right | + | '''int''' query(left: '''int''', right: '''int'''): |
| − | if left == | + | leftRes = ''neutral'' |
| − | + | rightRes = ''neutral'' | |
| − | + | '''while''' left < right | |
| − | + | '''if''' left '''mod''' 2 == 0 | |
| − | + | leftRes = leftRes <tex> \circ </tex> data[left] | |
| − | if right == | + | left = left '''div''' 2 |
| − | + | '''if''' right '''mod''' 2 == 1 | |
| − | + | rightRes = data[right] <tex> \circ </tex> rightRes | |
| − | + | right = right '''div''' 2 - 1 | |
| − | + | '''if''' left == right | |
| − | + | leftRes = leftRes <tex> \circ </tex> data[left] | |
| − | + | '''return''' leftRes <tex> \circ </tex> rightRes | |
| − | + | ||
| + | ==См. также== | ||
| + | * [[Реализация запроса в дереве отрезков сверху]] | ||
| + | |||
| + | ==Источники информации== | ||
| + | |||
| + | * [http://e-maxx.ru/algo/segment_tree MAXimal :: algo :: Дерево отрезков] | ||
| + | |||
| + | * [http://ru.wikipedia.org/wiki/%D0%94%D0%B5%D1%80%D0%B5%D0%B2%D0%BE_%D0%BE%D1%82%D1%80%D0%B5%D0%B7%D0%BA%D0%BE%D0%B2 Википедия {{---}} Дерево отрезков] | ||
| + | |||
| + | * [http://rain.ifmo.ru/cat/view.php/vis/trees/segment-2006 Визуализатор] | ||
| − | + | * [http://rain.ifmo.ru/cat/view.php/vis/trees/segment-2006/algorithm Алгоритм] | |
| − | [ | + | [[Категория: Дискретная математика и алгоритмы]] |
| − | [ | + | [[Категория: Дерево отрезков]] |
Текущая версия на 19:18, 4 сентября 2022
Содержание
Алгоритм
Реализация запроса снизу вверх в дереве отрезков является, в отличие от реализации запроса сверху вниз, итеративным методом. Будем рассматривать абстрактную операцию, обладающую свойством ассоциативности, и обозначать ее .
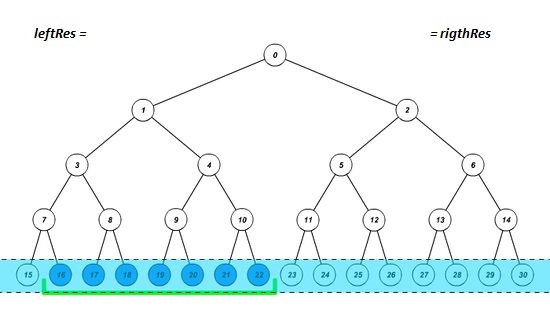
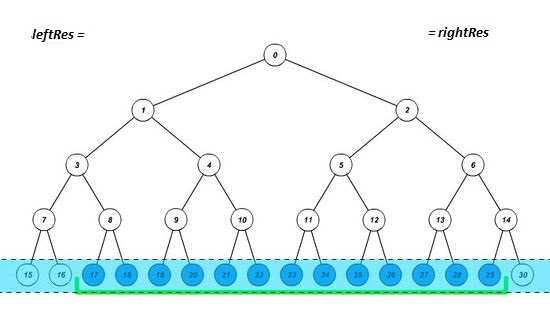
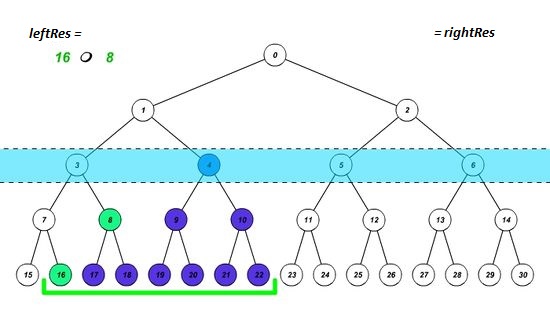
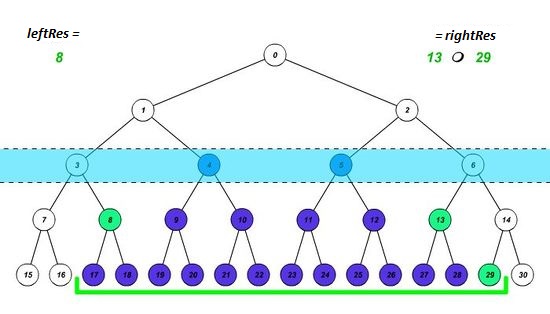
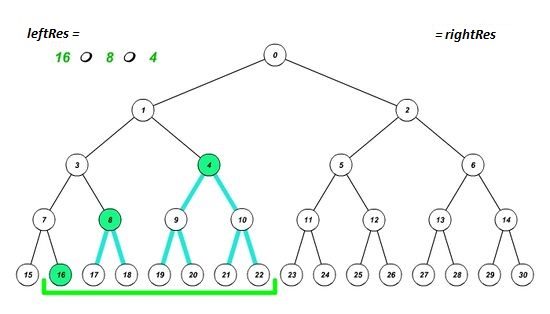
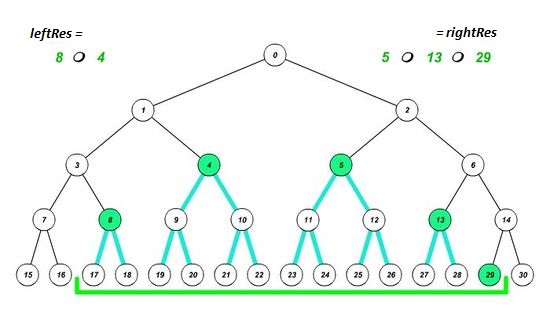
Построим дерево отрезков, и установим границы отрезка на соответствующие им листья. Будем действовать в 3 этапа:
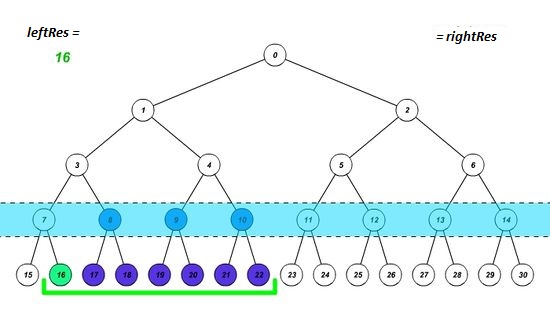
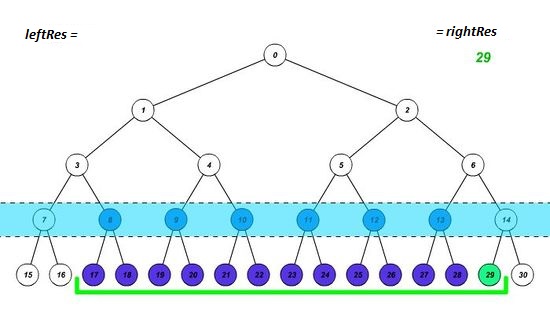
- Если элемент, попавший на левую границу, является правым сыном, то запишем в результат значение, полученное после выполнения нашей операции над предыдущим результатом и значением этого элемента, а левую границу перемещаем на один элемент вправо. Аналогично с правой границей (является ли она левым сыном). Таким образом мы учтем вклад нужной нам вершины и избавимся от вклада ненужного нам поддерева.
- Устанавливаем границы отрезка на родительские элементы текущих границ. Это позволит узнать, входит ли полученный отрезок в искомый или нет. Повторяем этап 1, пока границы не пересекутся.
- Если после завершения цикла границы совпадут, значит полученный отрезок входит в искомый, и надо пересчитать результат.
| Реализация запроса снизу вверх | Ещё один пример |
 |
|
 |
|
 |
|
 |
|
Псевдокод
Пусть результат считаем на отрезке . При этом значения и , передающиеся в функцию, должны указывать на листья дерева (необходимо увеличить значение на индекс массива, с которого начинаются листья). Переменные и будут собирать значения на отрезках, отделившихся соответственно слева или справа от рассматриваемого.
int query(left: int, right: int):
leftRes = neutral
rightRes = neutral
while left < right
if left mod 2 == 0
leftRes = leftRes data[left]
left = left div 2
if right mod 2 == 1
rightRes = data[right] rightRes
right = right div 2 - 1
if left == right
leftRes = leftRes data[left]
return leftRes rightRes