Лемма о единственном паросочетании в графе замен — различия между версиями
(Перенаправление на Граф замен#Лемма о единственном паросочетании в графе замен) |
|||
| (не показано 16 промежуточных версий 5 участников) | |||
| Строка 1: | Строка 1: | ||
| + | #перенаправление [[Граф замен#Лемма о единственном паросочетании в графе замен]] | ||
| + | {{Утверждение | ||
| + | |statement=Пусть [[Двудольные_графы_и_раскраска_в_2_цвета|двудольный граф]] <tex>G</tex> содержит единственное [[Связь_максимального_паросочетания_и_минимального_вершинного_покрытия_в_двудольных_графах#Связь_максимального_паросочетания_и_минимального_вершинного_покрытия_в_двудольном_графе|полное паросочетание]] <tex>M</tex>. Тогда можно упорядочить вершины левой <tex>(a_i \in A)</tex> и правой <tex>(b_i \in B)</tex> долей таким образом, что <tex>\forall j > i : (a_i b_j) \notin G</tex>. При этом рёбра паросочетания будут иметь вид <tex>(a_i b_i)</tex>. | ||
| + | |||
| + | |proof=Индукция по <tex>|A|</tex>.<br/> | ||
| + | * База | ||
| + | *: При <tex>|A|=1</tex> утверждение очевидно. <br/> | ||
| + | * Переход | ||
| + | *: Пусть <tex>|A|=n>1</tex> (для <tex>|A|=n-1</tex> утверждение верно). Возьмем произвольную вершину в левой доли. Будем строить из неё [[Теорема о максимальном паросочетании и дополняющих цепях#Паросочетание в двудольном графе|чередующуюся цепь]], добавляя по очереди ребро, входящее в <tex>M</tex>, и ребро, не входящее в <tex>M</tex>. Заметим, что такой путь не содержит циклов (циклы нечётной длины невозможны, так как граф двудольный, циклы чётной длины отсутствуют из-за единственности паросочетания). Если последнее добавленное ребро не принадлежит <tex>M</tex>, то присоединим к цепи ребро из <tex>M</tex>, инцидентное последней вершине. Значит, построение цепи прервется только при добавлении ребра из <tex>M</tex> при достижении вершины [[Основные определения теории графов#Степень вершины|степени]] <tex>1</tex>. <br/> | ||
| + | Таким образом, последнее ребро в цепи имеет вид <tex>(ab) \in M</tex>, где <tex>a \in A, b \in B, \deg b = 1</tex>. Положим <tex>a_n=a, b_n=b</tex>. Для <tex>G \setminus \{a_n \cup b_n \}</tex> утверждение верно по предположению индукции. С другой стороны, так как <tex>\deg b_n = 1</tex>, то <tex>(a_i b_n) \notin G</tex> при <tex>i<n</tex>, поэтому для <tex>j = n</tex> утверждение также верно.<br/> | ||
| + | }} | ||
| + | |||
| + | |||
{{Лемма | {{Лемма | ||
|about= | |about= | ||
| − | о единственном паросочетании графе замен | + | о единственном паросочетании в графе замен |
| − | |statement= Дан [[Определение матроида|матроид]] <tex>M = \langle X,I \rangle </tex>. Пусть двудольный граф <tex>G_M(A) = \{ (x, y) | + | |statement= Дан [[Определение матроида|матроид]] <tex>M = \langle X,I \rangle </tex>. Пусть двудольный граф <tex>G_M(A) = \{ (x, y) \mid x \in A, y \notin A, A \setminus x \cup y \in I \}</tex> содержит единственное полное паросочетание на <tex>A \oplus B</tex>, где <tex>A\in I</tex> и <tex>|A| = |B|</tex>. Тогда <tex>B \in I</tex>. |
|proof= | |proof= | ||
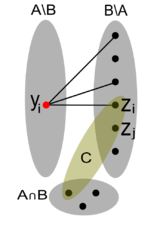
[[Файл:Graph replacement.png|thumb|left|160px|]] | [[Файл:Graph replacement.png|thumb|left|160px|]] | ||
| − | + | Упорядочим вершины левой <tex>(y_i \in A \setminus B)</tex> и правой <tex>(z_j \in B \setminus A)</tex> долей таким образом, что <tex>\forall j > i : (y_i z_j) \notin G_M(A)</tex>. При таком упорядочивании ребра паросочетания имеют вид <tex>(y_i z_i)</tex>. | |
| − | Требуется доказать, что <tex>B</tex> независимо. Предположим обратное. Пусть <tex>B \notin I</tex>, тогда существует [[Теорема о циклах|цикл]] <tex>C \subset B</tex>.<br/> Выберем минимальное <tex>i</tex> такое, что <tex> | + | Требуется доказать, что <tex>B</tex> независимо. Предположим обратное. Пусть <tex>B \notin I</tex>, тогда существует [[Теорема о циклах|цикл]] <tex>C \subset B</tex>.<br/> Выберем минимальное <tex>i</tex> такое, что <tex>z_i \in C</tex>. Так как <tex>\forall j > i : (y_i z_j) \notin G_M(A)</tex>, то <tex>A \setminus y_i \cup z_j \notin I</tex>, следовательно, <tex>C \setminus z_i \subset \langle A \setminus y_i \rangle </tex>. По [[Оператор замыкания для матроидов#theorem|свойствам замыкания 1 и 3]] получаем:<br/> |
<tex>C \setminus z_i \subset \langle A \setminus y_i \rangle \Rightarrow \langle C \setminus z_i \rangle \subset \langle \langle A \setminus y_i \rangle \rangle \Rightarrow \langle C \setminus z_i \rangle \subset \langle A \setminus y_i \rangle</tex> <br/> | <tex>C \setminus z_i \subset \langle A \setminus y_i \rangle \Rightarrow \langle C \setminus z_i \rangle \subset \langle \langle A \setminus y_i \rangle \rangle \Rightarrow \langle C \setminus z_i \rangle \subset \langle A \setminus y_i \rangle</tex> <br/> | ||
| − | + | Так как <tex>z_i \in \langle C \setminus z_i \rangle \subset \langle A \setminus y_i \rangle</tex>, то <tex>A \setminus y_i \cup z_i \notin I</tex>, то есть в <tex>G_M(A)</tex> не существует ребра <tex>(y_i z_i)</tex>. Но тогда, как было отмечено ранее, не существует полного паросочетания. Получили противоречие. | |
}} | }} | ||
| + | |||
| + | == Источники информации == | ||
| + | * [http://www.cs.illinois.edu/class/sp10/cs598csc/Lectures/Lecture16.pdf '''Chandra Chekuri — Combinatorial Optimization], с. 6 | ||
| + | |||
| + | [[Категория:Алгоритмы и структуры данных]] | ||
| + | [[Категория:Матроиды]] | ||
| + | [[Категория:Пересечение матроидов]] | ||
Текущая версия на 10:04, 27 апреля 2016
Перенаправление на:
| Утверждение: |
Пусть двудольный граф содержит единственное полное паросочетание . Тогда можно упорядочить вершины левой и правой долей таким образом, что . При этом рёбра паросочетания будут иметь вид . |
|
Индукция по .
|
| Лемма (о единственном паросочетании в графе замен): |
Дан матроид . Пусть двудольный граф содержит единственное полное паросочетание на , где и . Тогда . |
| Доказательство: |
|
Упорядочим вершины левой и правой долей таким образом, что . При таком упорядочивании ребра паросочетания имеют вид . Требуется доказать, что независимо. Предположим обратное. Пусть , тогда существует цикл . |