2-3 дерево — различия между версиями
(→Операции) |
IRomchig (обсуждение | вклад) |
||
| Строка 1: | Строка 1: | ||
[[Файл:23дерево_new.jpg |right|300px|thumb|Пример 2-3 дерева]] | [[Файл:23дерево_new.jpg |right|300px|thumb|Пример 2-3 дерева]] | ||
| − | ''' 2-3 дерево ''' — структура данных, | + | ''' 2-3 дерево ''' — структура данных, представляющая собой [[B-дерево|B-дерево]] cтепени 1, такое что из каждого узла может выходить две или три ветви. |
| − | |||
| − | |||
| − | |||
== Структура == | == Структура == | ||
| − | + | Все данные хранятся в листьях, в вершинах хранится вспомогательная информация,необходимая для организации поиска по поддеревьям. Нелистовые вершины содержат 1 или 2 ключа, указывающие на диапазон значений в их поддеревьях. 2-3 деревья сбалансированы, то есть каждое левое, правое, и центральное поддерево одинаковой высоты, и таким образом содержат равное (или почти равное) число данных. | |
== Свойства == | == Свойства == | ||
| Строка 14: | Строка 11: | ||
* 2-3 дерево - сливаемое дерево | * 2-3 дерево - сливаемое дерево | ||
* Все пути от корня до любого листа имеют одинаковую длину | * Все пути от корня до любого листа имеют одинаковую длину | ||
| − | * Высота 2-3 дерева | + | * Высота 2-3 дерева <tex>O(\log{n})</tex>, где <tex> n </tex> - количество элементов в дереве. |
Поэтому операции над ним выполняются за время <tex>O(\log{n})</tex>. | Поэтому операции над ним выполняются за время <tex>O(\log{n})</tex>. | ||
== Операции == | == Операции == | ||
| − | + | === Поиск === | |
Для поиска в 2-3 дереве необходимо последовательно просматривать ключи, | Для поиска в 2-3 дереве необходимо последовательно просматривать ключи, | ||
хранящиеся во внутренних ячейках, спускаясь от корня к листьям. Вначале ключ искомого | хранящиеся во внутренних ячейках, спускаясь от корня к листьям. Вначале ключ искомого | ||
| Строка 27: | Строка 24: | ||
в среднее поддерево, а если превосходит, то идем в правое поддерево. | в среднее поддерево, а если превосходит, то идем в правое поддерево. | ||
| − | + | === Вставка элемента === | |
Есть два варианта вставки в 2-3 дерево. | Есть два варианта вставки в 2-3 дерево. | ||
| Строка 38: | Строка 35: | ||
[[Файл:23treeadd1.png|245px|border]] [[Файл:23treeadd2.png|200px|border]] | [[Файл:23treeadd1.png|245px|border]] [[Файл:23treeadd2.png|200px|border]] | ||
| − | + | === Удаление элемента === | |
При удалении ключа из узла возникают три варианта. | При удалении ключа из узла возникают три варианта. | ||
| Строка 51: | Строка 48: | ||
[[Файл:23treedel3.png|200px|border]] [[Файл:23treedel4.png|215px|border]] | [[Файл:23treedel3.png|200px|border]] [[Файл:23treedel4.png|215px|border]] | ||
| − | + | === Слияние двух деревьев === | |
Возможно два варианта слияния двух деревьев. | Возможно два варианта слияния двух деревьев. | ||
| Строка 67: | Строка 64: | ||
[http://ru.wikipedia.org/wiki/2-3-дерево 2-3 дерево] | [http://ru.wikipedia.org/wiki/2-3-дерево 2-3 дерево] | ||
| − | Дональд Кнут Искусство программирования, том 3. Сортировка и поиск | + | Дональд Кнут Искусство программирования, том 3. Сортировка и поиск |
Версия 01:40, 27 марта 2012
2-3 дерево — структура данных, представляющая собой B-дерево cтепени 1, такое что из каждого узла может выходить две или три ветви.
Содержание
Структура
Все данные хранятся в листьях, в вершинах хранится вспомогательная информация,необходимая для организации поиска по поддеревьям. Нелистовые вершины содержат 1 или 2 ключа, указывающие на диапазон значений в их поддеревьях. 2-3 деревья сбалансированы, то есть каждое левое, правое, и центральное поддерево одинаковой высоты, и таким образом содержат равное (или почти равное) число данных.
Свойства
- Все нелистовые вершины содержат один ключ и 2 поддерева или 2 ключа и 3 поддерева.
- Все листовые вершины находятся на одном уровне (на нижнем уровне) и содержат 1 или 2 ключа.
- Все данные отсортированы
- 2-3 дерево - сливаемое дерево
- Все пути от корня до любого листа имеют одинаковую длину
- Высота 2-3 дерева , где - количество элементов в дереве.
Поэтому операции над ним выполняются за время .
Операции
Поиск
Для поиска в 2-3 дереве необходимо последовательно просматривать ключи, хранящиеся во внутренних ячейках, спускаясь от корня к листьям. Вначале ключ искомого элемента сравнивается с первым ключом ячейки и, если искомый ключ не больше первого, то осуществляется переход в левое поддерево. Иначе, сравниваем искомый ключ со вторым ключом в ячейке (если второго ключа нет — поддерева всего два, то сразу переходим во второе поддерево) и если наш ключ не превосходит второй ключ, то осуществляется переход в среднее поддерево, а если превосходит, то идем в правое поддерево.
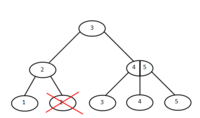
Вставка элемента
Есть два варианта вставки в 2-3 дерево.
Чтобы поместить новый ключ в узел, в котором содержится ровно один ключ, необходимо просто добавить его как второй ключ к узлу.
Если же в узле уже содержатся два ключа, делим его на два "одноключевых" узла и вставляем средний ключ в родительский узел.Это может привести к тому, что придется делить родительский узел. Тогда таким же образом проходим до корня дерева.
Удаление элемента
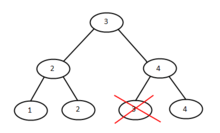
При удалении ключа из узла возникают три варианта.
Если после удаления ключа в узле содержится два ключа, то после удаления ничего не меняется.
Если же у ключа после удаления остался один элемент, то проверяем количество потомков второго ребенка того узла, ребенком которого является узел с удаляемым ключом. Если у него два ребенка, то присваиваем ему оставшийся один элемент. Вершину, оставшуюся без детей, удаляем рекурсивно.
Иначе у него три ребенка. Тогда присваиваем узлу с одним ключом один из этих ключей, таким образом получая два узла с двумя ключами.
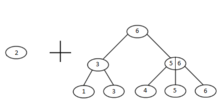
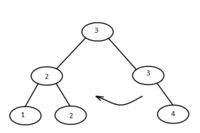
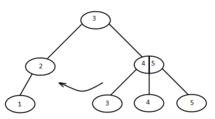
Слияние двух деревьев
Возможно два варианта слияния двух деревьев.
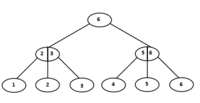
Если два дерева одной высоты, то слияние представляет собой добавление общей вершины.
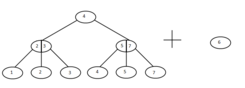
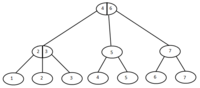
Если два дерева разной высоты, то при слиянии меньшее добавляем как поддерево к одной из вершин большего.Если возникает ситуация,когда у необходимого узла уже есть три ребенка, то делим его на два узла с двумя поддеревьями и проверяем родителя.Таким образом проходим по дереву вверх до полной сбалансировки.
Дополнительные ссылки
Использованные источники
Дональд Кнут Искусство программирования, том 3. Сортировка и поиск