Основные определения теории графов

Эта статья находится в разработке!

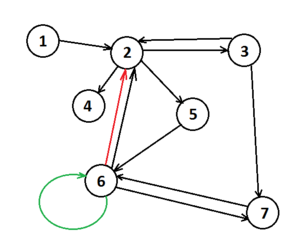
Ориентированные графы (directed graph)

Ориентированный граф
Красным выделено ребро (6, 2)
Зеленым обозначена петля (6, 6)

Определение:

Ориентированным графом [math]G[/math] называется пара [math]G = (V, E)[/math], где [math]V[/math] - конечное множество вершин, а [math] E \subset V \times V [/math] - множество рёбер.

а) мультиграф
б) псевдограф

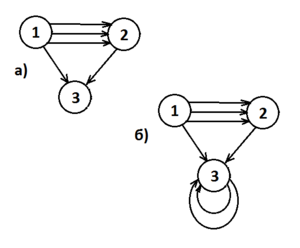
Есть еще более другое определение. Ориентированным графом [math]G[/math] называется четверка [math]G = (V, E, beg, end)[/math] , где [math]beg, end : E \rightarrow V [/math], а [math]V[/math] и [math]E[/math] - некоторые абстрактные множества. Иногда граф, построенный таким образом называют мультиграфом. В мультиграфе не допускаются петли (см. определение ниже), но пары вершин допускается соединять более чем одним ребром. Такие ребра называются кратными (иначе - параллельные).

Определение:

Ребром (дугой) ориентированного графа называют упорядоченную пару вершин [math] (v, u) \in E [/math].

В ориентированном графе ребро, концы которого совпадают, то есть [math]e=\{v,v\}[/math], называется петлей. Мультиграф с петлями принято называть псевдографом.
Если имеется ребро [math] (v, u) \in E [/math], то иногда говорят, что [math] u [/math] - родитель [math] v [/math]. Также вершины [math] u [/math] и [math] v [/math] называют смежными. Граф с [math] p [/math] вершинами и [math] q [/math] ребрами называют [math] (p, q) [/math] - графом. [math] (1, 0) [/math] - граф называют тривиальным.

Определение:

Полустепенью входа вершины [math]v_i[/math] называется число рёбер, входящих в эту вершину, и обозначается [math]deg^+v_i[/math]. Аналогично, полустепенью выхода вершины [math]v_i[/math] называется число рёбер, выходящих из этой вершины, и обозначается [math]deg^-v_i[/math].

Определение:

Путём в графе называется последовательность вида [math]v_0 e_1 v_1 ... e_k v_k[/math], где [math]e_i = (v_{i-1}, v_i)[/math].

Определение:

Циклическим путём называется путь, в котором [math]v_0 = v_k[/math].

Определение:

Цикл - это класс эквивалентности циклических путей на отношении эквивалентности таком, что два пути эквивалентны, если [math] \exists j : \forall i \Rightarrow e_{(i \mod k)} = e'_{(i + j) \mod k}[/math]; где [math]e[/math] и [math]e'[/math] - это две последовательности ребер в циклическом пути.