Детерминированные конечные автоматы

Основные понятия

Определение:

Детерминированный конечный автомат (ДКА) — набор из пяти элементов [math]\langle \Sigma , Q, s \in Q, T \subset Q, \delta : Q \times \Sigma \to Q \rangle[/math], где [math]\Sigma[/math] — алфавит, [math]Q[/math] — множество состояний, [math]s[/math] — начальное (стартовое) состояние, [math]T[/math] — множество допускающих состояний, [math]\delta[/math] — функция переходов.

Процесс допуска

Опишем процесс допуска автоматом слова [math]p[/math]. Изначально автомат находится в стартовом состоянии [math]s[/math]. При считывании очередного символа [math]p_i[/math] автомат переходит в состояние [math]\delta(q, p_i)[/math], где [math]q[/math] — текущее состояние автомата. Процесс продолжается до тех пор, пока не будет достигнут конец входного слова.

Определение:

Будем говорить, что автомат допускает слово, если после окончания описанного выше процесса с этим словом автомат окажется в допускающем состоянии.

Замечание. Если в какой-то момент из текущего состояния нет перехода по считанному символу, то будем считать, что автомат не допускает данное слово. При реализации вместо отдельного рассмотрения данного случая иногда удобно вводить фиктивную нетерминальную «дьявольскую вершину», из которой любой переход ведет в неё же саму, и заменить все несуществующие переходы на переходы в «дьявольскую вершину».

Примеры

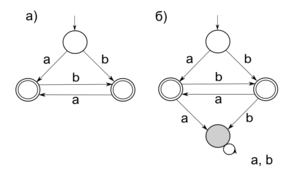
Автомат, принимающий непустые строки из чередующихся символов a и b а)без «дьявольской вершины» б)с «дьявольской вершиной» (отмечена серым цветом) [math]\bigcirc[/math] — нетерминальное состояние [math]\circledcirc[/math] — терминальное состояние Стрелка [math]\downarrow[/math] указывает на начальное состояние
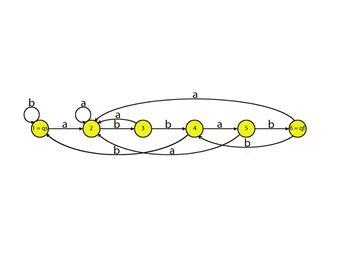
Автомат для поиска образца в тексте для строки abbab

Автоматные языки

Определение:

Мгновенное описание (конфигурация) — пара [math]\langle q, \alpha \rangle[/math], где [math]q[/math] – текущее состояние, [math]\alpha[/math] – оставшиеся символы.

Будем говорить, что конфигурация [math]\langle p, \beta \rangle[/math] выводима из [math]\langle q, \alpha \rangle[/math] за 1 шаг [math](\langle q, \alpha \rangle \vdash \langle p, \beta \rangle)[/math], если:

• [math]\alpha = c\beta[/math]
• [math]\delta (q, c)=p [/math]

Будем говорить, что конфигурация [math]\langle p, \beta \rangle[/math] выводима из [math]\langle q, \alpha \rangle[/math] за конечное число шагов [math](\langle q, \alpha \rangle \vdash^* \langle p, \beta \rangle)[/math], если [math]\exists n:[/math]

• [math]\alpha = c_1 c_2 ... c_n\beta[/math]
• [math]\langle q, c_1 c_2 c_3 ... c_n\beta \rangle \vdash \langle u_1, c_2 c_3 ... c_n\beta \rangle \vdash \langle u_2, c_3 ... c_n\beta \rangle \vdash ... \vdash \langle u_{n-1}, c_n\beta \rangle \vdash \langle p, \beta \rangle[/math]

Лемма:

[math]\langle q, \alpha \rangle \vdash^* \langle p, \varepsilon \rangle, \langle p, \beta \rangle \vdash^* \langle r, \varepsilon \rangle \Rightarrow \langle q, \alpha\beta \rangle \vdash^* \langle r, \varepsilon \rangle[/math]

Доказательство:

[math]\triangleright[/math]

[math]\langle q, \alpha\beta \rangle \vdash^* \langle p, \beta \rangle \vdash^* \langle r, \varepsilon \rangle.[/math]

[math]\triangleleft[/math]

Определение:

Множество [math]L(\mathcal{A})=\{\alpha| \langle s, \alpha \rangle \vdash^* \langle t, \varepsilon \rangle t \in T\}[/math] называется языком автомата [math]\mathcal{A}[/math]. Множество языков всех ДКА образует множество автоматных языков [math]Aut[/math].

Иначе говоря, языком автомата является множество всех допускаемых им слов. Произвольный язык является автоматным, если существует ДКА, допускающий те и только те слова, которые принадлежат языку.

Способы представления автомата

• Диаграмма переходов — граф, в котором состояниям соответствуют вершины, а рёбрам — переходы между состояниям
• Таблица переходов [math]T (|Q| \times |\Sigma|)[/math], дающая табличное представление функции [math]\delta[/math].

См. также

• Недетерминированные конечные автоматы
• Автомат для поиска образца в тексте
• Алгоритм Ахо-Корасик

Литература

• Хопкрофт Д., Мотвани Р., Ульман Д. — Введение в теорию автоматов, языков и вычислений, 2-е изд. : Пер. с англ. — Москва, Издательский дом «Вильямс», 2002. — 528 с. : ISBN 5-8459-0261-4 (рус.)