Конфигурация — различия между версиями
(Новая страница: «{{В разработке}} <wikitex> {{Определение |id=arrangement |definition = '''Конфигурацией'''(англ. ''arrangement'') $\mathcal{A...») |
(asymptote, я твой дом труба шатал) |
||
| Строка 1: | Строка 1: | ||
{{В разработке}} | {{В разработке}} | ||
| + | |||
| + | == Основные определения == | ||
<wikitex> | <wikitex> | ||
| Строка 11: | Строка 13: | ||
|id=cell | |id=cell | ||
|definition = | |definition = | ||
| − | '''Ячейкой'''(англ. ''cell'') размерности $k$, где $0 \le k | + | '''Ячейкой'''(англ. ''cell'') размерности $d$ в $\mathcal{A}(\mathcal{H})$ называется максимальная связная область в $R^d$, не пересекаемая ни одной гиперплоскостью в $\mathcal{H}$. |
| + | |||
| + | Ячейкой размерности $k$, где $0 \le k < d$ в $\mathcal{A}(\mathcal{H})$ называется максимальная связная область в пересечении гиперплоскостей подмножества $\mathcal{S} \in \mathcal{H}$, которая не пересекается ни одной гиперплоскостью из множества $\mathcal{H} \setminus \mathcal{S}$. | ||
}} | }} | ||
| + | |||
| + | === Пояснения === | ||
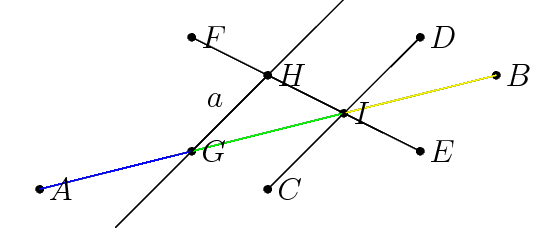
| + | Рассмотрим примеры для $R^2$, в нём гиперплоскостями являются прямые, лучи и отрезки, а конкретно, $\mathcal{H} = \{AB, CD, EF, a\}$ | ||
| + | |||
| + | {|align="left" | ||
| + | | [[Файл:2-cells.png | 250x150 px | frame | Цветами выделены ячейки размерности 2(на R^2 - грани). Жёлтая и зелёная ячейки не ограничены, синяя - ограничена.]] | ||
| + | | [[Файл:1-cells.png | 250x150 px | frame | Взяв множество S с единственным отрезком AB, получим три ячейки размерности 1(на R^2 - рёбра). Взяв за множество S поочерёдно CD, EF и a, получим остальные ячейки размерности 1.]] | ||
| + | | [[Файл:0-cells.png | 250x150 px | frame | Взяв поочерёдно за множество S множества {a, EF}, {a, AB}, {AB, CD, EF}, получим ячейки G, H и I размерности 0(на R^2 - вершины)]] | ||
| + | |} | ||
Версия 11:57, 1 ноября 2011
Эта статья находится в разработке!
Основные определения
<wikitex>
| Определение: |
| Конфигурацией(англ. arrangement) $\mathcal{A}(\mathcal{H})$ называется разбиение $\mathbb{R}^d$ в связные открытые(топологически) ячейки размерностей $0, 1 \dots d $ множеством $\mathcal{H}$ гиперплоскостей в $ \mathbb{R}^d$. |
| Определение: |
| Ячейкой(англ. cell) размерности $d$ в $\mathcal{A}(\mathcal{H})$ называется максимальная связная область в $R^d$, не пересекаемая ни одной гиперплоскостью в $\mathcal{H}$. Ячейкой размерности $k$, где $0 \le k < d$ в $\mathcal{A}(\mathcal{H})$ называется максимальная связная область в пересечении гиперплоскостей подмножества $\mathcal{S} \in \mathcal{H}$, которая не пересекается ни одной гиперплоскостью из множества $\mathcal{H} \setminus \mathcal{S}$. |
Пояснения
Рассмотрим примеры для $R^2$, в нём гиперплоскостями являются прямые, лучи и отрезки, а конкретно, $\mathcal{H} = \{AB, CD, EF, a\}$
Источники
- Goodman J.E., O'Rourke J. Handbook of discrete and computational geometry. p. 537, 2004, 2nd edition.
</wikitex>